فیلتر اکتیو پایین گذر — از صفر تا صد

از طریق ترکیب یک فیلتر پایین گذر پسیو ساده RC با یک تقویت‌کننده عملیاتی یا اپ امپ می‌توان یک فیلتر اکتیو پایین گذر (Active Low Pass Filter) را ایجاد کرد. در این مطلب قصد داریم به بررسی مدار این نوع از فیلترها بپردازیم.

در مطلب فیلتر پایین گذر پسیو با استفاده از مدار RC، دیدیم که یک مدار فیلتر پسیو مرتبه اول ساده مانند فیلتر پایین گذر پسیو یا فیلتر بالا گذر پسیو را می‌توان با استفاده از فقط یک مقاومت متصل به یک خازن غیرقطبی پیاده‌سازی کرد و سپس باید به مدار یک سیگنال ورودی سینوسی اعمال شود. می‌دانیم که یکی از بزرگ‌ترین معایب فیلتر پایین گذر این است که دامنه سیگنال خروجی از آن کمتر از دامنه سیگنال ورودی به فیلتر است. به عبارت دیگر، بهره در یک فیلتر پایین گذر پسیو هیچ وقت بزرگ‌تر از واحد نمی‌شود و ایراد دیگر فیلتر در این است که امپدانس بار روی منحنی مشخصه فیلتر تاثیر خواهد گذاشت.

به دلیل اینکه مدار یک فیلتر پسیو از چند طبقه تشکیل می‌شود، این کاهش دامنه ورودی که به آن میرایی (Attenuation) گفته می‌شود، می‌تواند به میزان شدیدی صورت گیرد. یک روش برای بازیابی و یا کنترل کاهش دامنه سیگنال، این است که از خاصیت تقویت‌کنندگی (Amplification) با استفاده از فیلترهای اکتیو (Active Filters) بهره ببریم.

همان طور که از نام این نوع از فیلترها مشخص است، فیلتر اکتیو شامل ادوات اکتیو مانند تقویت‌کننده عملیاتی و ترانزیستور پیوندی دوقطبی یا ترانزیستور FET در مدار خود است. این فیلترها توان خود را از یک منبع توان خارجی به دست می‌آورند و از آن برای ارتقا یا تقویت سیگنال خروجی استفاده می‌کنند. تقویت‌کنندگی در فیلترها را همچنین می‌توان برای شکل دادن و یا تغییر پاسخ فرکانسی مدار فیلتر مورد استفاده قرار داد. از طریق این کار یک پاسخ خروجی بسیار گزینشی‌تر ایجاد می‌شود و پهنای باند فیلتر بسیار باریک‌تر و یا پهن‌تر می‌شود. بنابراین می‌توان گفت که تفاوت اصلی بین یک فیلتر اکتیو با یک فیلتر پسیو در تقویت‌کنندگی موجود در فیلتر اکتیو است.

یک فیلتر اکتیو معمولا از یک تقویت‌کننده عملیاتی یا اپ امپ در طراحی مدار خود استفاده می‌کند. می‌دانیم که یک اپ امپ دارای امپدانس ورودی بزرگی است. همچنین این المان امپدانس خروجی بسیار کوچکی دارد و بهره ولتاژ آن توسط شبکه مقاومتی موجود در حلقه فیدبک مشخص می‌شود.

برخلاف یک فیلتر بالا گذر پسیو، که در تئوری دارای بیشینه پاسخ فرکانس برابر با بی‌نهایت است، بیشینه پاسخ فرکانسی در یک فیلتر اکتیو، به بهره یا پهنای باند (یا بهره حلقه باز) تولید شده توسط اپ امپ مورد استفاده محدود می‌شود. طراحی یک فیلتر اکتیو بسیار ساده‌تر از طراحی یک فیلتر پسیو انجام می‌گیرد. یک فیلتر اکتیو مشخصه عملکردی بسیار بهتری را تولید می‌کند و هنگامی که در یک طراحی مداری خوب مورد استفاده قرار گیرد، سطح نویز بسیار پایینی خواهد داشت. همچنین این فیلتر از دقت بسیار خوبی نسبت به فیلتر نوع پسیو برخوردار است.

فیلتر اکتیو پایین گذر مرتبه اول

یکی از متداول‌ترین و قابل فهم‌ترین انواع فیلترهای اکتیو، فیلتر اکتیو پایین گذر است. اصول عملکردی این نوع از فیلترها و همچنین پاسخ فرکانسی آن‌ها، دقیقا با فیلتر نوع پایین گذر پسیو مشابه است. اما تنها تفاوت بین این دو نوع فیلتر پایین گذر در این است که از تقویت‌کننده عملیاتی به منظور تقویت‌کنندگی و کنترل بهره در ساختار یک فیلتر اکتیو استفاده می‌شود.

فیلم آموزش الکترونیک 3 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

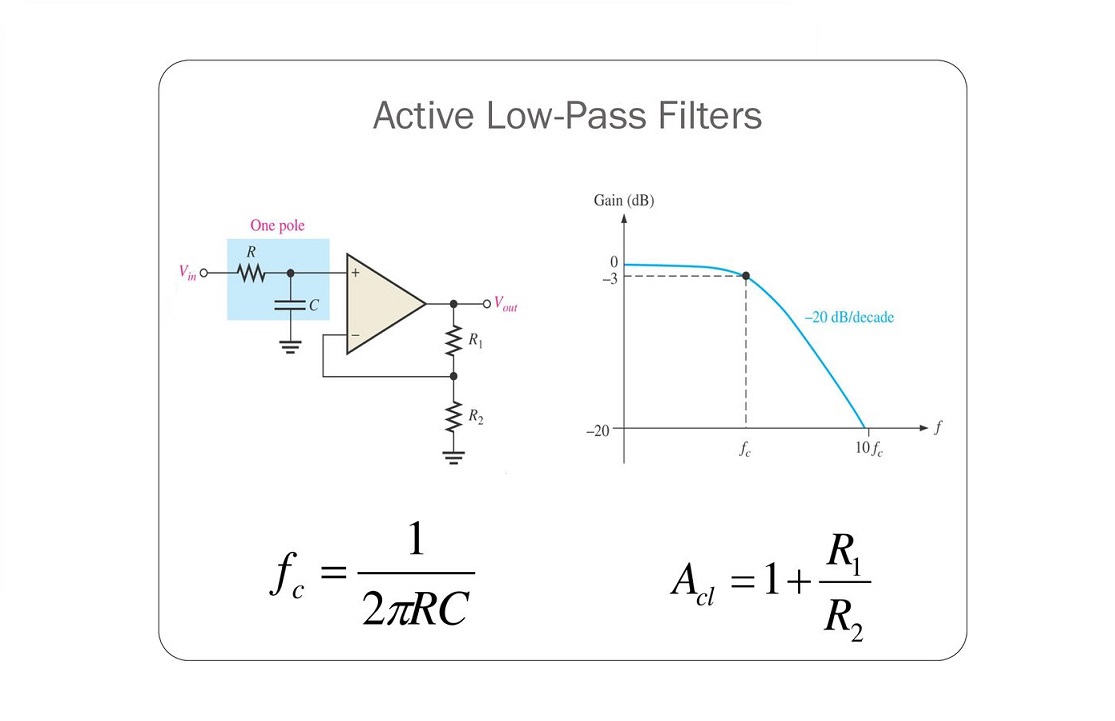
ساده‌ترین فرم یک فیلتر اکتیو پایین گذر این است که یک تقویت‌کننده معکوس کننده یا غیر معکوس کننده را به مدار فیلتر پایین گذر RC متصل کرد. نمایی از یک فیلتر اکتیو پایین گذر در تصویر زیر نشان داده شده است.

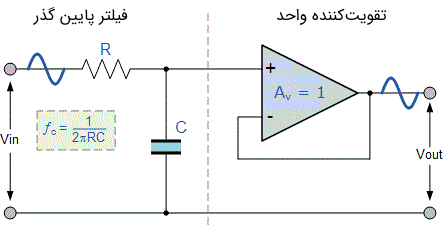
این فیلتر مرتبه اول اکتیو پایین گذر ساده از یک طبقه فیلتر پسیو RC تشکیل شده است که یک مسیر فرکانس پایین به ورودی غیر معکوس کننده اپ امپ فراهم می‌کند. تقویت‌کننده به عنوان یک مدار تقیب‌کننده ولتاژ یا بافر پیکربندی شده است که دارای بهره ولتاژ DC واحد $$A_V = 1$$ است و از این نظر با فیلتر پایین گذر پسیو اختلاف دارد؛ زیرا فیلتر پسیو دارای بهره ولتاژ DC کمتر از واحد است.

مزیت اصلی مدار فیلتر اکتیو این است که امپدانس ورودی بالای اپ امپ مانع از اضافه بار در خروجی فیلتر می‌شود و از طرف دیگر، امپدانس پایین خروجی اپ امپ منجر به این می‌شود که نقطه فرکانس قطع فیلتر تحت تاثیر تغییرات در امپدانس بار قرار نگیرد.

در حالیکه این پیکربندی پایداری خوبی را برای فیلتر فراهم کرده است، اما یک عیب بزرگ مدار فیلتر فوق این است که قادر به ایجاد بهره ولتاژ بزرگ‌تر از یک نیست. البته با اینکه بهره ولتاژ واحد است، اما بهره توان بسیار بزرگ است؛ زیرا امپدانس خروجی آن بسیار پایین‌تر از امپدانس ورودی آن است.

فیلتر اکتیو پایین گذر با تقویت‌کننده

اگر به یک فیلتر اکتیو پایین گذر با بهره ولتاژ بزرگ‌تر از یک احتیاج داشته باشیم، آن‌گاه می‌توان از مدار زیر استفاده کرد.

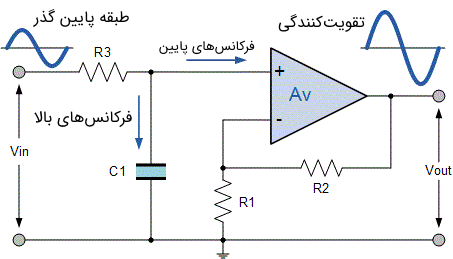
در تصویر فوق، مدار یک فیلتر اکتیو پایین گذر با تقویت‌کنندگی (Active Low Pass Filter with Amplification) را مشاهده می‌کنید. در این مدار، پاسخ فرکانسی شبیه به پاسخ فرکانسی متعلق به یک فیلتر RC پسیو است، البته با این تفاوت که دامنه سیگنال خروجی از فیلتر، توسط بهره باند میانی $$A_F$$ مربوط به تقویت‌کننده افزایش می‌یابد.

فیلم آموزش طراحی فیلتر و سنتز مدار در فرادرس

کلیک کنید

برای یک مدار تقویت‌کننده غیر معکوس کننده دامنه بهره ولتاژ مربوط به فیلتر بر حسب تابعی از حاصل تقسیم مقاومت فیدبک $$R_2$$ بر مقاومت مربوط به ورودی $$R_1$$ به دست می‌آید و به صورت زیر خواهد بود:

$$\text {DC gain} = ( 1 + \frac {R_ 2} { R _ 1 })$$

بنابراین می‌توان بهره فیلتر پایین گذر اکتیو را به عنوان تابعی از فرکانس به این صورت نوشت:

$$ \text {Voltage gain (A_V)} = \frac {V_ {out}} {V _ {in}} = \frac {A _ F} { \sqrt{ 1 + (\frac {f} {f_c}) ^ 2} } $$

که در فرمول فوق، $$A_F$$ برابر با بهره باند میانی فیلتر، $$f$$ فرکانس سیگنال ورودی بر حسب هرتز و $$f_c$$ فرکانس قطع فیلتر بر حسب هرتز هستند.

بنابراین، عملکرد یک فیلتر اکتیو پایین گذر را می‌توان با استفاده از بهره فرکانسی فوق به دست آورد. بر این اساس می‌توان گفت:

1. در فرکانس‌های بسیار پایین ($$f < f_c$$)، رابطه $$\frac {V_ { out }} {V _ {in }} \cong A_F$$ برقرار است.
2. در فرکانس قطع ($$f = f_c$$)، رابطه $$\frac {V_ { out }} {V _ {in }} = \frac { A_F } { \sqrt{2}} = 0.707 A_F$$ صادق است.
3. برای فرکانس‌های بسیار بالا ($$f > f_c$$)، رابطه $$\frac {V_ { out }} {V _ {in }} < A_F$$ برقرار است.

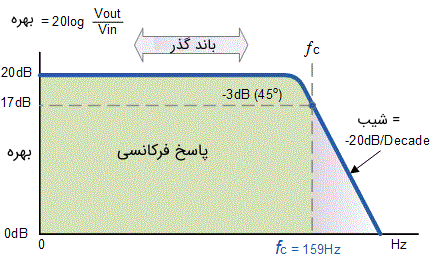
بنابراین، فیلتر پایین گذر اکتیو دارای بهره ثابت $$A_F$$ از صفر تا نقطه قطع فرکانس بالا $$f_c$$ است. در نقطه $$f_c$$ بهره برابر با $$0.707 A_F$$ می‌شود و در فرکانس‌های بزرگ‌تر از $$f_c$$ با افزایش فرکانس، مقدار بهره با یک نرخ ثابت کاهش می‌یابد. به همین دلیل است که زمانی که فرکانس به اندازه ده برابر افزایش یابد، بهره ولتاژ تقسیم بر ده می‌شود.

به عبارت دیگر، هر بار که فرکانس با ضریب ده افزایش یابد، بهره به اندازه ۲۰ دسیبل کاهش می‌یابد. در مورد مدارات فیلتری، دامنه بهره میان گذر مدار معمولا بر حسب دسیبل یا dB به عنوان تابعی از بهره ولتاژ بیان می‌شود. در حالت کلی می‌توان دامنه بهره ولتاژ را به صورت زیر نوشت:

$$ A_V (dB ) = 20 \; log \; _ {10} (\frac { V _ {out }} { V_ {in}}) $$

$$ \therefore \; -3 dB = 20 \; log \; _ {10} ( 0.707 \; \frac { V _ {out }} { V_ {in}}) $$

مثال ۱: فیلتر اکتیو پایین گذر

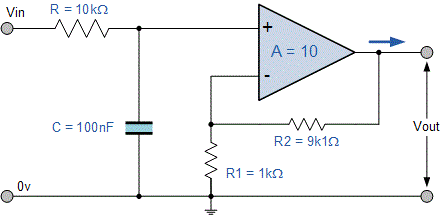
مدار یک فیلتر اکتیو پایین گذر غیر معکوس کننده را به صورتی طراحی کنید که بهره ولتاژ برابر با ۱۰ در فرکانس‌های پایین داشته باشد و نیز فرکانس قطع بالا یا فرکانس گوشه آن ۱۵۹ هرتز و امپدانس ورودی آن ۱۰ کیلو اهم باشد.

فیلم آموزش الکترونیک 3 – مرور و حل مساله در فرادرس

کلیک کنید

حل

بهره ولتاژ یک تقویت‌کننده عملیاتی غیر معکوس کننده به صورت زیر محاسبه می‌شود:

$$A_F = 1 + \frac {R _ 2} {R _ 1} = 10$$

فرض کنید مقدار مقاومت $$R_1$$ برابر با ۱ کیلو اهم باشد. فرمول فوق را مجددا بازنویسی می‌کنیم و به صورت زیر می‌نویسیم:

$$R _ 2 = (10 - 1) \times R _ 1 = 9 \times 1 \; K \Omega = 9 K \Omega$$

بنابراین برای بهره ولتاژ برابر با ۱۰، مقدار مقاومت $$R_1$$ برابر با ۱ کیلو اهم و مقاومت $$R_2$$ برابر با ۹ کیلو اهم خواهد بود. البته توجه کنید که مقاومت ۹ کیلو اهم در واقع وجود ندارد و به جای آن باید از مقاومت ۹٫۱ کیلو اهم استفاده شود. با تبدیل این بهره ولتاژ به مقدار معادل آن بر حسب دسیبل، به مقدار زیر می‌رسیم:

$$\text {Gain in dB} = 20 log A = 20 log 10 = 20dB$$

فرکانس قطع یا فرکانس گوشه $$f_c$$ برابر با ۱۵۹ هرتز با امپدانس ورودی ۱۰ کیلو اهم است. این فرکانس قطع را می‌توان با استفاده از فرمول زیر به دست آورد:

$$f_c = \frac { 1 } { 2 \pi R C } HZ$$

از طریق بازآرایی فرمول استاندارد فوق، می‌توان مقدار خازن C را به صورت زیر محاسبه کرد:

$$C = \frac { 1 } { 2 \pi f_c R } = \frac { 1 } { 2 \pi \times 159 \times 10 K \Omega} = 100 n F$$

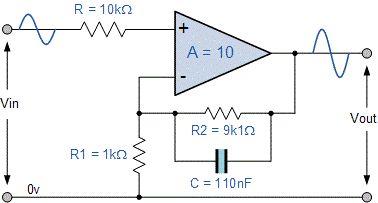
بنابراین مدار فیلتر اکتیو پایین گذر با این فرکانس کاری، به صورت زیر خواهد بود.

همچنین منحنی پاسخ فرکانسی فیلتر به صورت زیر ترسیم می‌شود.

اگر امپدانس خارجی متصل به ورودی مدار فیلتر تغییر کند، این تغییر امپدانس روی فرکانس قطع نیز تاثیر می‌گذارد. یک راه برای جلوگیری از هرگونه تاثیر خارجی روی فرکانس قطع فیلتر، این است که خازن را به صورت موازی با مقاومت فیدبک $$R_2$$ در مدار قرار داد. این روش قادر است مقاومت $$R_2$$ را به صورت موثری از ورودی حذف کند، در حالی که منحنی مشخصه فیلتر همچنان ثابت حفظ شود.

با این حال، مقدار خازن به آهستگی از مقدار ۱۰۰ نانو فاراد تا ۱۱۰ نانو فاراد تغییر می‌کند تا مقدار مقاومت ۹٫۱ کیلو اهم نیز به حساب آید. اما فرمول مربوط به محاسبه فرکانس قطع فیلتر همچنان مشابه با فرمول مربوط به فیلتر پایین گذر پسیو RC و به صورت زیر است:

$$f_c = \frac { 1 } { 2 \pi C R _ 2 }$$

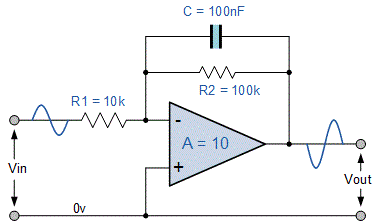
بنابریان مدار ساده شده مربوط به یک فیلتر پایین گذر اکتیو غیرمعکوس‌ کننده به صورت زیر است.

همچنین مدار فیلتر تقویت‌کننده معکوس‌ کننده اکتیو به صورت زیر ترسیم می‌شود.

فیلتر پایین گذر اکتیو در تقویت‌کننده‌های صوتی، سیستم‌های بلندگو و اکولایزرها (Equalizers) بیشتر کاربرد دارد. این مدارات، سیگنال‌های بم (Bass) دارای فرکانس پایین را به بلندگوهای بم بزرگ هدایت می‌کنند و یا هر نویز فرکانس بالا یا اعوجاج از نوع هیس (Hiss) را کاهش می‌دهند. مدارات فیلتر پایین گذر هنگامی که در کاربردهای صوتی مورد استفاده قرار می‌گیرند، به آن‌ها فیلتر ارتقا بم (Bass Boost) نیز گفته می‌شود.

فیلتر اکتیو پایین گذر مرتبه دو

همانند فیلترهای نوع پسیو، یک فیلتر اکتیو پایین گذر مرتبه اول را نیز می‌توان به سادگی به یک فیلتر اکتیو پایین گذر مرتبه دو تبدیل کرد. برای این هدف باید یک شبکه RC اضافی در مسیر ورودی به مدار اضافه شود. در تصویر زیر نمایی از مدار یک فیلتر اکتیو پایین گذر مرتبه دو را می‌توان مشاهده کرد.

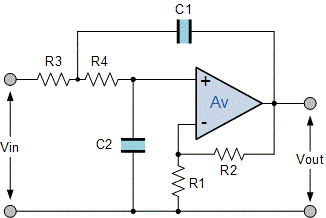
در مورد این فیلتر، می‌توان بهره ولتاژ را به صورت زیر محاسبه کرد:

$$A_ V = 1 + \frac { R_2 } { R_1 }$$

همچنین فرکانس قطع فیلتر اکتیو پایین گذر مرتبه دو فوق را می‌توان با استفاده از فرمول زیر به دست آورد:

$$f_c = \frac { 1 } { 2 \pi \sqrt{ R_3 R_4 C_1 C_2 }}$$

نمودار پاسخ فرکانسی یک فیلتر اکتیو پایین گذر مرتبه دو بسیار مشابه با یک فیلتر پایین گذر مرتبه اول است، البته این دو فیلتر با یکدیگر تفاوت‌هایی نیز دارند. در فیلتر اکتیو پایین گذر مرتبه دو، باند توقف و رول آف (Roll-off) دو برابر یک فیلتر اکتیو پایین گذر مرتبه اول است و در $$40 \; dB / octave$$ قرار دارد.

فیلم آموزش الکترونیک 3 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

رول آف در یک فیلتر عبارت است از تضعیف تدریجی مشخصه پاسخ دامنه با تغییر فرکانس پس از قسمت تخت نمودار. بنابراین مراحل طراحی یک فیلتر پایین گذر اکتیو مرتبه دوم، مشابه با مراحل طراحی یک فیلتر اکتیو پایین گذر مرتبه اول است.

زمانی که مدارات چند فیلتر را برای ایجاد فیلترهای درجه بالاتر با یکدیگر به صورت آبشاری متصل می‌کنیم، بهره کلی فیلتر برابر با حاصل ضرب بهره تک تک طبقات در نظر گرفته می‌شود. به عنوان مثال، بهره یک طبقه ممکن است برابر با ۱۰ و بهره طبقه دوم برابر با ۳۲ و بهره طبقه سوم از فیلتر برابر با ۱۰۰ باشد. در این شرایط، بهره کلی فیلتر برابر با حاصل ضرب این سه مقدار، یعنی 32000 خواهد بود. نمایی از یک فیلتر متشکل از سه طبقه با بهره‌های ولتاژ مختلف را می‌توان در تصویر زیر مشاهده کرد.

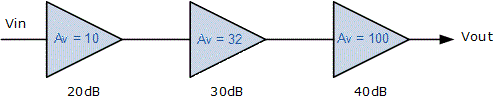
در مورد فیلتر تصویر فوق، می‌توان بهره ولتاژ را بر حسب دسیبل به صورت زیر محاسبه کرد:

$$A_ V = A_ {V 1} \times A_ {V 2} \times A_ {V 3}$$

$$A_ V = 10 \times 32 \times 100 = 32000$$

$$A_ V (dB) = 20 \; log _{ 10} (32000)$$

$$A_ V (dB) = 90\; dB$$

برای محاسبه بهره ولتاژ فیلتر بر حسب دسیبل، می‌توان از رابطه زیر نیز بهره گرفت:

$$90\; dB = 20 \; dB + 30 \; dB + 40 \; dB$$

یک فیلتر اکتیو پایین گذر مرتبه دو، دارای دو قطب است. این نوع از فیلترها از اهمیت بالایی برخوردارند؛ زیرا فیلترهای از مراتب بالاتر را می‌توان با کمک آن‌ها طراحی و پیاده‌سازی کرد. از طریق اتصال آبشاری فیلترهای مرتبه اول و دوم به یکدیگر، می‌توان فیلترهایی از هر مرتبه، تا هر عدد دلخواه زوج یا فرد را به وجود آورد.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی برق
• آموزش الکترونیک ۳
• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش طراحی فیلتر و سنتز مدار
• تقویت کننده لگاریتمی و آنتی لگاریتمی — از صفر تا صد
• اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
• فیلتر میان گذر پسیو — از صفر تا صد

^^