ساختمان داده در جاوا — از صفر تا صد

در این مقاله به بحث ساختمان داده در جاوا (Java Data Structures) و انواع آن پرداخته شده است. انواع ساختمان داده در جاوا به دو دسته کلی ساختمان داده خطی و ساختمان داده غیر خطی در جاوا تقسیم میشود. از جمله ساختمان دادههای خطی در جاوا میتوان به آرایه، لیست پیوندی، پشته و ساختمان داده صف اشاره کرد. همچنین ساختمانهای داده غیرخطی شامل درخت دودویی، ساختمان داده پیشوندی، هرمی (Heap) و گراف میشود. در طول بخشهای مختلف این نوشتار، مثالهای متعددی به زبان جاوا برای هر یک از انواع ساختمان داده ارائه شده است.
از آنجایی که ساختمان دادهها (Data Structures) هسته اصلی هر زبان برنامه نویسی به حساب میآیند و انتخاب یک ساختمان داده خاص بر کارایی و عملکرد برنامههای زبان برنامه نویسی جاوا (Java) تأثیرات فراوانی میگذارد، بنابراین یادگیری ساختمان دادههای مختلف موجود در جاوا از الزامات این زبان برنامه نویسی محسوب میشود. در هنگام برنامه نویسی، از ساختمان داده برای ذخیره و سازماندهی دادهها استفاده میشود، سپس الگوریتمها (Algorithm) برای ویرایش و طراحی ساختمان دادهها مورد استفاده قرار میگیرند. از این رو به دلیل اهمیت بالای ساختمان داده و همچنین برنامه نویسی همهمنظوره جاوا، در مقاله «ساختمان داده در جاوا» به بررسی ساختمان دادهها در این زبان برنامه نویسی پر کاربرد پرداخته شده است.
ساختمان داده در جاوا چیست؟
به طور کلی و به بیان ساده ساختمان دادهها به روشهای مختلف ذخیرهسازی دادهها روی کامپیوتر گفته میشود. ساختمان داده در جاوا روشی برای ذخیرهسازی و سازماندهی دادهها در کامپیوتر است تا بتوان از دادهها به طور مؤثر و در مسیری کارآمد استفاده کرد. ساختمان دادهها در جاوا و هر زبان برنامه نویسی دیگر ابزاری برای مدیریت کارآمد حجم بسیاری از دادهها به حساب میآید.
همچنین، استفاده از ساختمان داده مناسب باعث ایجاد امکان طراحی و نوشتن الگوریتمهای بهتری برای دادههای مورد نظر میشود. ساختمان دادهها در جاوا تقریباً در هر زمینهای از علوم کامپیوتر (Computer Science) مورد استفاده قرار میگیرند که برخی از آنها شامل گرافیک کامپیوتری (Computer Graphic)، سیستم عاملها (Operating System | OS)، هوش مصنوعی (Artificial Intelligence | AI)، طراحی کامپایلر (Compiler Design) و بسیاری از موارد دیگر میشوند.

در بخش بعدی مقاله «ساختمان داده در جاوا» به این موضوع پرداخته شده است که چرا به ساختمان دادهها در جاوا نیاز است؟
چرا به ساختمان داده در جاوا نیاز است؟
از آنجایی که مقدار دادهها در پروژهها به سرعت رو به افزایش است، برنامهها روز به روز پیچیدهتر میشوند و مشکلاتی برای آنها پیش میآید که برخی از این مشکلات در ادامه فهرست شدهاند:
- سرعت پردازش: به دلیل افزایش روز افزون حجم دادهها، به سرعت بالایی برای مدیریت حجم آنها نیاز است. اما امکان دارد که پردازنده نتواند این مقدار از دادهها را پردازش کند.
- جست و جوی دادهها: موجودیتی با سایز ۲۰۰ مورد در نظر گرفته شده است. اگر برنامه قصد جست و جوی یک مورد خاص را داشته باشد، باید همه این ۲۰۰ مورد را پیمایش کند تا به هدف خود برسد. این کار سرعت فرآیند جست و جو را کاهش میدهد.
- چندین درخواست در یک زمان یکسان: فرض میشود که میلیونها کاربر در حال جست و جوی دادهها به صورت همزمان در سرور تحت وب هستند، پس احتمال به وجود آمدن مشکل برای سرور افزایش پیدا میکند.
برای حل مشکلات فوق، از ساختمان دادهها در جاوا استفاده میشود. در ساختمان دادههای جاوا ، دادهها به گونهای ذخیره و مدیریت میشوند که دادههای مورد نیاز را میتوان به وسیله جستوجو فوراً به دست آورد. بخش بعدی این مقاله به بررسی مزایای استفاده از ساختمان داده در جاوا اختصاص دارد.
مزایای استفاده از ساختمان داده در جاوا چه هستند؟
همانطور که در بخش قبلی به آن اشاره شد، استفاده از ساختمان داده در جاوا میتواند برخی از مشکلات برنامهها را از بین ببرد.
همچنین، ساختمان دادههای جاوا مزایای بسیاری هم دارند که در این بخش به آنها اشاره شده است:
- کارایی (Efficiency): ساختمان داده در جاوا برای افزایش کارایی و عملکرد برنامهها به وسیله سازماندهی دادهها به گونهای استفاده میشود که دادهها نیازمند فضای کم همراه با سرعت پردازش بالا باشند.
- قابلیت استفاده مجدد (Reusability): ساختمان داده قابلیت استفاده مجدد از دادهها را در برنامه فراهم میکند. بعد از پیادهسازی یک ساختمان داده خاص میتوان آن را بارها در برنامهها و مکانهای دیگر مورد استفاده قرار داد. همچنین، میتوان ساختمان داده را در کتابخانهها (Library) پیادهسازی و از این کتابخانهها در برنامه نویسی با روشهای گوناگون استفاده کرد.
- انتزاع یا تجرید (Abstraction): در زبان جاوا نوع انتزاعی دادهها (Abstract Data Type | ADT) برای مشخص کردن ساختمان داده استفاده میشود. «ADT» سطحی از انتزاع را فراهم میکند. کاربران در برنامههایشان از ساختمان دادهها در جاوا با کمک واسطها (Interface) استفاده میکنند، بدون اینکه از جزئیات پیادهسازی ساختمان دادهها آگاهی داشته باشند.
بخش بعدی مقاله «ساختمان داده در جاوا» به طبقهبندی انواع گوناگون ساختمان دادهها در جاوا اختصاص داده شده است.
طبقه بندی ساختمان داده در جاوا چگونه است؟
در این بخش از مقاله به بررسی انواع ساختمان دادهها در جاوا پرداخته میشود. ساختمان دادههای اصلی در جاوا به دو دسته ساختمان دادههای خطی (Linear Data Structures) و ساختمان دادههای غیر خطی (Non Linear Data Structure) یا سلسله مراتبی (Hierarchical Data Structures) تقسیم میشوند که هر کدام دارای انواع گوناگونی به صورت زیر هستند:
- ساختمان دادههای خطی
- ساختمان داده ایستا یا ثابت (Static)
- آرایه (Array)
- ساختمان داده پویا (Dynamic)
- لیست پیوندی (Linked List)
- پشته (Stack)
- صف (Queue)
- ساختمان داده ایستا یا ثابت (Static)
- ساختمان دادههای غیر خطی
- درخت (Tree)
- درخت دودویی (Binary Tree)
- درخت جست و جوی دودویی (Binary Search tree | BST)
- درخت پیشوندی (Trie Tree)
- هرم (Heap)
- گراف (Graph)
- مجموعه (Set)
- جدول درهمسازی (Hash Table)
- درخت (Tree)
همچنین، انواع ساختمان دادههای اصلی در نمودار زیر ارائه شدهاند:
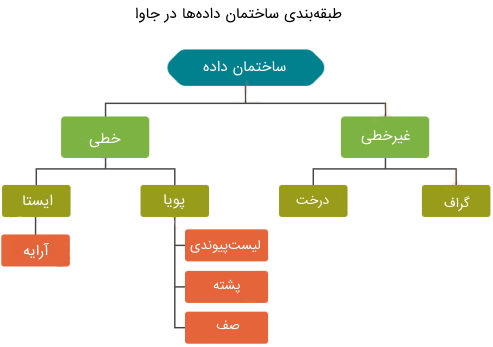
بخشهای بعدی مقاله «ساختمان داده در جاوا» به بررسی هر یک از انواع ساختمان دادههای فوق اختصاص داده شدهاند. در بخش بعدی، ابتدا ساختمان دادههای خطی شرح داده شده است.
ساختمان داده خطی در جاوا چیست؟
ساختمان داده خطی در جاوا نوعی از ساختمان دادهها به حساب میآید که عناصر آن به صورت متوالی و به ترتیب قرار گرفتهاند. ساختمان داده خطی یک ساختمان داده تک سطحی (Single Level Data Structure) است. در این نوع ساختمان داده، فقط یک عنصر اول وجود دارد که دارای یک عنصر بعدی و فقط یک عنصر آخر وجود دارد که دارای یک عنصر قبلی است و همه عناصر دیگر این ساختمان دادهها در جاوا دارای یک عنصر قبلی و یک عنصر بعدی هستند. ب
خش بعدی مقاله به معرفی و بررسی ساختمان داده آرایه در جاوا اختصاص دارد.

ساختمان داده آرایه در جاوا چیست؟
آرایه (Array) یک ساختمان داده خطی و ایستا است که گروهی از عناصر مشابه را نشان میدهد که توسط اندیسها (Index) میتوان به آنها دسترسی پیدا کرد. معمولاً، سایز آرایه در جاوا قبل از ذخیره دادهها در آن مشخص میشود. اولین آدرس آرایه متعلق به اولین عنصر است و آخرین آدرس به آخرین عنصر آرایه تعلق دارد.
ویژگیهای ساختمان داده آرایه در جاوا در ادامه فهرست شدهاند:
- آرایهها دارای دادههای ساده با نوع داده یکسان مانند عدد صحیح (Integer)، عدد اعشاری (Float) یا حتی نوع دادهای که کاربر تعریف کرده است (User Defined Data type) مانند ساختمانها و اشیا هستند. همچنین، همه عناصر اندازهای (Size) یکسان دارند.
- برخی از انواع داده رایج در آرایهها به عنوان نوع دادهای پایه آنها شناخته میشوند.
- معمولاً آرایهها در جاوا به عنوان شی در نظر گرفته میشوند.
- اندیسهای (Index) مقادیر آرایهها با عدد صفر شروع میشوند.
- قبل از استفاده از آرایهها باید آنها را برای ذخیره دادهها تعریف کرد.
- محل ذخیره آرایهها در جاوا به صورت تخصیص پویا (Dynamic Allocation) در ناحیه Heap است.
- عناصر آرایه در جاوا در مکانهای حافظه به هم پیوسته (Contiguous Memory Location) ذخیره میشوند و تخصیص داده اولین عنصر از کوچکترین مکان حافظه شروع میشود.
- عناصر آرایه در جاوا به صورت تصادفی (Randomly) قابل دسترسی هستند.
- ساختمان داده آرایه در جاوا به طور کامل پویا (Dynamic) نیست.
- طول آرایهها در جاوا را میتوان به وسیله متُد یا همان تابع «Length» پیدا کرد.
- سایز آرایه باید به صورت مقدار عدد صحیح باشد.

تصویر فوق یک ساختمان داده آرایه را در جاوا نشان میدهد. در سمت چپ آن اولین عنصر و اندیس، و در سمت راست آن آخرین عنصر و اندیس مشاهده میشوند. برای مثال، اگر در یک بازی ویدیویی قصد ذخیره ۱۰ امتیاز آخر بازی وجود داشته باشد. به جای استفاده از ده متغیر گوناگون برای هر امتیاز، میتوان از یک گروه آرایهای برای همه امتیازها استفاده کرد و با استفاده از اندیسها امتیازات بالا و پایین را مشخص کرد. پیچیدگیهای زمانی آرایه در جاوا برای عملیات گوناگون آن به صورت زیر است:
- دسترسی به عناصر : (۱)O
- جست و جو:
- جست و جوی متوالی (Sequential Search): (n)O
- جست و جوی دودویی (Binary Search) در صورتی که آرایه مرتب باشد: (log n)O
- درج: (n)O
- حذف: (n)O
باید به این نکته توجه داشت فقط زمانی میتوان از آرایه استفاده کرد که تعداد عناصر و اندازه آن از قبل مشخص شده باشد، زیرا حافظه آرایه، قبل از پردازش ایجاد میشود. به همین دلیل آرایهها در دسته ساختمان دادههای ایستا قرار میگیرند. کدهای زیر مثالی برای پیادهسازی برنامهای با استفاده از ساختمان داده آرایه در جاوا است:
1package org.arpit.java2blog;
2
3import java.util.Arrays;
4public class StringArrayMain {
5
6 public static void main(String[] args) {
7 String[] strArr = {"One","Two","Three"};
8
9 System.out.println("Array elements are:");
10 // تکرار روی آرایه
11 for (int i=0;i<strArr.length;i++)
12 {
13 System.out.println(strArr[i]);
14 }
15 System.out.println("====================");
16 System.out.println("Printing array elements using Arrays.toString():");
17 System.out.println("====================");
18 // .برای چاپ آرایه استفاده کرد Arrays.toString() میتوان از آرایه
19 System.out.println(Arrays.toString(strArr));
20 }
21}خروجی کدهای فوق به صورت زیر نشان داده شده است:
Array elements are: One Two Three ==================== Printing array elements using Arrays.toString(): ==================== [One, Two, Three]
- مقالههای پیشنهادی:
در بخش بعدی مقاله «ساختمان داده در جاوا» ساختمان داده لیست پیوندی مورد بررسی قرار میگیرد.
ساختمان داده لیست پیوندی در جاوا چیست؟
لیست پیوندی (Linked List) یک نوع ساختمان داده خطی و پویا در جاوا به حساب میآید که دارای مجموعهای از انواع مشابه عناصر داده به نام گره (Node) است. در این نوع از ساختمان دادهها در جاوا هر عنصر دادههای خود را ذخیره و به مکان ذخیره عنصر بعدی به وسیله اشارهگر (Pointer) اشاره میکند. عنصر آخر به «تهی» (Null) اشاره دارد و این نشان دهنده تمام شدن زنجیره است. گره اول در لیست پیوندی «رأس» (Head) و گره آخر در آن «انتها» (Tail) نامگذاری شده است.
لیست پیوندی برخی از اشکالات آرایه در جاوا را برطرف کرده است زیرا در این نوع ساختمان داده در جاوا نیازی به تعریف تعداد عناصر قبل از استفاده از آنها نیست، بنابراین تخصیص یا عدم تخصیص حافظه میتواند در حین انجام پردازش و طبق نیاز آن باشد و همچنین، درج و حذف عناصر در آن بسیار سادهتر است. در این نوع ساختمان داده در جاوا سه نوع لیست پیوندی یک طرفه، دو طرفه و حلقوی وجود دارند که در ادامه این بخش معرفی شدهاند:
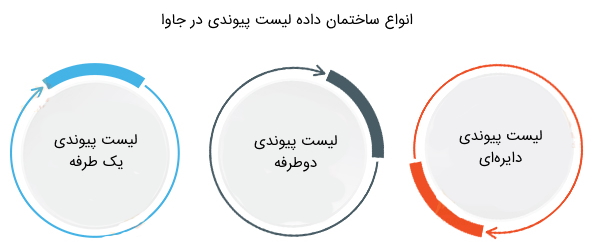
لیست تک پیوندی یا یک طرفه
لیست تک پیوندی یا یک طرفه یا تک جهتی (Singly Linked List | Uni Directional) همانطور که در تصویر زیر مشخص است، فقط به صورت رو به جلو و در یک جهت میتواند دادهها را دریافت کند.
این نوع لیست پیوندی به عنوان لیست پیوندی یک طرفه نیز شناخته میشود زیرا حاوی یک گره و یک اشارهگر واحد است که به گره بعد از خود اشاره میکند.

در ادامه برای درک بهتر و آشنایی با لیست پیوندی، مثالی برای لیست پیوندی یک طرفه ارائه شده است:
1package org.arpit.java2blog.datastructures;
2
3class Node {
4 public int data;
5 public Node next;
6
7 public void displayNodeData() {
8 System.out.println("{ " + data + " } ");
9 }
10}
11
12public class MyLinkedList {
13 private Node head;
14
15 public boolean isEmpty() {
16 return (head == null);
17 }
18
19 // متد درج گره در ابتدای لیست پیوندی
20 public void insertFirst(int data) {
21 Node newHead = new Node();
22 newHead.data = data;
23 newHead.next = head;
24 head = newHead;
25 }
26
27 // متد حذف گره از ابتدای لیست پیوندی
28 public Node deleteFirst() {
29 Node temp = head;
30 head = head.next;
31 return temp;
32 }
33
34 // متد برای حذف گره ارائه شده در برنامه
35 public void deleteAfter(Node after) {
36 Node temp = head;
37 while (temp.next != null && temp.data != after.data) {
38 temp = temp.next;
39 }
40 if (temp.next != null)
41 temp.next = temp.next.next;
42 }
43
44 // متد برای درج در انتهای لیست پیوندی
45 public void insertLast(int data) {
46 Node current = head;
47 while (current.next != null) {
48 current = current.next; // تهی شود، حلقه ایجاد خواهد شد current.next تا زمانی که
49 }
50 Node newNode = new Node();
51 newNode.data = data;
52 current.next = newNode;
53 }
54
55 // متد برای چاپ لیست پیوندی
56 public void printLinkedList() {
57 System.out.println("Printing LinkedList (head --> last) ");
58 Node current = head;
59 while (current != null) {
60 current.displayNodeData();
61 current = current.next;
62 }
63 System.out.println();
64 }
65
66 public static void main(String args[])
67 {
68 MyLinkedList myLinkedlist = new MyLinkedList();
69 myLinkedlist.insertFirst(50);
70 myLinkedlist.insertFirst(60);
71 myLinkedlist.insertFirst(70);
72 myLinkedlist.insertFirst(10);
73 myLinkedlist.insertLast(20);
74 myLinkedlist.printLinkedList();
75 // لیست پیوندی به صورت زیر خواهد بود:
76 // 10 -> 70 -> 60 -> 50 -> 20
77
78 System.out.println("=========================");
79 System.out.println("Delete node after Node 60");
80 Node node=new Node();
81 node.data=60;
82 myLinkedlist.deleteAfter(node);
83 // پس از حذف گره بعد از ۱، لیست پیوندی به صورت زیر خواهد بود:
84 // 10 -> 70 -> 60 -> 20
85
86 System.out.println("=========================");
87 myLinkedlist.printLinkedList();
88 }
89}خروجی برنامه فوق که نشان دهنده انواع عملیات در لیست پیوندی یک طرفه است، به صورت زیر نمایش داده میشود:
Printing LinkedList (head –> last)
{ 10 }
{ 70 }
{ 60 }
{ 50 }
{ 20 }
=========================
Delete node after Node 60
=========================
Printing LinkedList (head –> last)
{ 10 }
{ 70 }
{ 60 }
{ 20 }
لیست پیوندی دو طرفه
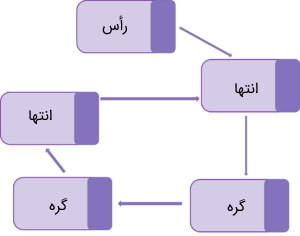
لیست پیوندی دو طرفه یا همان دو جهته (Doubly Linked List | Bi Directional) در دو جهت یعنی هم به صورت رو به جلو و هم به صورت رو به عقب میتواند دادهها را دریافت کند. دارای دو اشارهگر است که یکی از آنها به گره قبلی و یکی از آنها به گره بعدی اشاره میکنند.
این نوع لیست پیوندی پیمایش از دو طرف لیست را ممکن میسازد. تصویر زیر برای درک بهتر این نوع از ساختمان دادهها در جاوا ارائه شده است.

در ادامه مثالی برای لیست پیوندی دو طرفه ارائه شده است:
1package org.arpit.java2blog.datastructures;
2
3class Node {
4 public int data;
5 public Node next;
6 public Node prev;
7
8 public void displayNodeData() {
9 System.out.println("{ " + data + " } ");
10 }
11}
12
13public class MyDoublyLinkedList {
14
15 private Node head;
16 private Node tail;
17 int size;
18
19 public boolean isEmpty() {
20 return (head == null);
21 }
22
23 // متد برای درج گره در ابتدای لیست پیوندی
24 public void insertFirst(int data) {
25 Node newNode = new Node();
26 newNode.data = data;
27 newNode.next = head;
28 newNode.prev=null;
29 if(head!=null)
30 head.prev=newNode;
31 head = newNode;
32 if(tail==null)
33 tail=newNode;
34 size++;
35 }
36
37 // متد برای درج گره در انتهای لیست پیوندی
38 public void insertLast(int data) {
39 Node newNode = new Node();
40 newNode.data = data;
41 newNode.next = null;
42 newNode.prev=tail;
43 if(tail!=null)
44 tail.next=newNode;
45 tail = newNode;
46 if(head==null)
47 head=newNode;
48 size++;
49 }
50 // متد حذف گره از ابتدای لیست پیوندی دو طرفه
51 public Node deleteFirst() {
52
53 if (size == 0)
54 throw new RuntimeException("Doubly linked list is already empty");
55 Node temp = head;
56 head = head.next;
57 head.prev = null;
58 size--;
59 return temp;
60 }
61
62 // متد حذف گره از انتهای لیست پیوندی دو طرفه
63 public Node deleteLast() {
64
65 Node temp = tail;
66 tail = tail.prev;
67 tail.next=null;
68 size--;
69 return temp;
70 }
71
72 // متد برای حذف گره پس از یک گره خاص
73 public void deleteAfter(Node after) {
74 Node temp = head;
75 while (temp.next != null && temp.data != after.data) {
76 temp = temp.next;
77 }
78 if (temp.next != null)
79 temp.next.next.prev=temp;
80 temp.next = temp.next.next;
81
82 }
83
84 // (Forward) متد چاپ لیست پیوندی دو طرفه رو به جلو
85 public void printLinkedListForward() {
86 System.out.println("Printing Doubly LinkedList (head --> tail) ");
87 Node current = head;
88 while (current != null) {
89 current.displayNodeData();
90 current = current.next;
91 }
92 System.out.println();
93 }
94
95 // (Backward) متد چاپ لیست پیوندی دو طرفه رو به عقب
96 public void printLinkedListBackward() {
97 System.out.println("Printing Doubly LinkedList (tail --> head) ");
98 Node current = tail;
99 while (current != null) {
100 current.displayNodeData();
101 current = current.prev;
102 }
103 System.out.println();
104 }
105
106 public static void main(String args[])
107 {
108 MyDoublyLinkedList mdll = new MyDoublyLinkedList();
109 mdll.insertFirst(50);
110 mdll.insertFirst(60);
111 mdll.insertFirst(70);
112 mdll.insertFirst(10);
113 mdll.insertLast(20);
114 mdll.printLinkedListForward();
115 mdll.printLinkedListBackward();
116
117 System.out.println("================");
118 // :لیست پیوندی دو طرفه به صورت زیر خواهد بود
119 // 10 -> 70 -> 60 -> 50 -> 20
120
121 Node node=new Node();
122 node.data=10;
123 mdll.deleteAfter(node);
124 mdll.printLinkedListForward();
125 mdll.printLinkedListBackward();
126 // :بعد از حذف نود پس از ۱، لیست پیوندی به صورت زیر خواهد شد
127 // 20 -> 10 -> 60-> 50
128 System.out.println("================");
129 mdll.deleteFirst();
130 mdll.deleteLast();
131
132 // :پس از انجام عملیات فوق، لیست پیوندی به صورت زیر خواهد شد
133 // 60 -> 50
134 mdll.printLinkedListForward();
135 mdll.printLinkedListBackward();
136 }
137}خروجی مثال فوق که مثالی برای ساختمان داده لیست پیوندی دو طرفه در جاوا است به صورت زیر نمایش داده میشود:
Printing Doubly LinkedList (head –> tail)
{ 10 }
{ 70 }
{ 60 }
{ 50 }
{ 20 }
Printing Doubly LinkedList (tail –> head)
{ 20 }
{ 50 }
{ 60 }
{ 70 }
{ 10 }
================
Printing Doubly LinkedList (head –> tail)
{ 10 }
{ 60 }
{ 50 }
{ 20 }
Printing Doubly LinkedList (tail –> head)
{ 20 }
{ 50 }
{ 60 }
{ 10 }
================
Printing Doubly LinkedList (head –> tail)
{ 60 }
{ 50 }
Printing Doubly LinkedList (tail –> head)
{ 50 }
{ 60 }
لیست پیوندی حلقوی
در لیست پیوندی حلقوی یا دایرهای (Circular Linked List) گرهها میتوانند به صورت دایرهای مانند شکل زیر باهم در ارتباط باشند. در این لیست پیوندی هیچ گره تهی وجود ندارد و هر گرهای را میتوان به عنوان گره اول تعریف کرد.
لیست پیوندیهای دو طرفه در پیادهسازی صفهای دایرهای مؤثر هستند.
به عنوان مثال یک لیست پیوندی وجود دارد که به عنوان زنجیرهای از گیرههای کاغذ بهم متصل شدهاند. میتوان به راحتی یک گیره کاغذ دیگر به بالا یا پایین آن اضافه کرد. حتی گاهی امکان اضافه کردن یک گیره کاغذ به وسط این زنجیره نیز وجود دارد. تنها کاری که برای این وظیفه باید انجام شود این است که زنجیره از وسط قطع و گره جدید به آن اضافه شود و مجدداً زنجیرهها را بهم متصل کرد. لیست پیوندی نیز دقیقاً شبیه به همین مثال است. پیچیدگیهای زمانی برای انواع عملیات در ساختمان داده لیست پیوندی در جاوا به صورت زیر محاسبه میشوند:
- پیمایش عناصر: (n)O
- جست و جو یک عنصر: (n)O
- درج: (1)O
- حذف: (1)O
در ساختمان داده لیست پیوندی چند عملیات دیگر نیز وجود دارند که برخی از آنها شامل ادغام دو لیست پیوندی، تقسیمبندی لیستها و معکوس کردن لیست میشوند.
ساختمان داده پشته در جاوا چیست؟
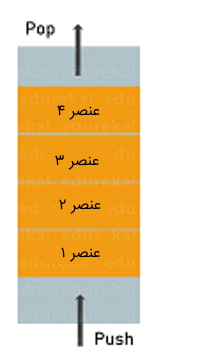
پشته یا همان «Stack» یک ساختمان داده انتزاعی در جاوا به حساب میآید. پشته مجموعهای از اشیا است که درج (Insert) و حذف (Remove) آنها توسط اصل «آخرین ورودی، اولین خروجی» یا «خروج به ترتیب عکس ورود» (Last In First Out | LIFO) انجام میشود. اشیا را میتوان در هر زمان در پشته درج کرد، اما فقط آخرین شی درج شده را در هر زمان میتوان حذف کرد. زمانی که یک پشته به عنوان آرایه پیادهسازی میشود، همه ویژگیهای آرایه را به ارث میبرد و اگر پشته به عنوان لیست پیوندی پیادهسازی شود، تمام ویژگیهای لیست پیوندی را به دست میآورد.
در ادامه بخش ویژگیهای پشته ارائه شده است:
- ساختمان داده پشته در جاوا، یک لیست مرتب است که در آن درج و حذف فقط از یک سمت آن یعنی بالای پشته انجام میشود.
- پشته، دارای ساختمان داده بازگشتی در بالای لیست است.
- ساختمان داده پشته از اصل «LIFO» پیروی میکند.
- سه متد اساسی زیر در پشته پشتیبانی میشوند:
- (e)Push (برای گذاشتن داده): قرار دادن یک عنصر مانند e در بالای پشته
- ()Pop (برای برداشتن داده با حذف آن داده): عنصر بالایی (Top) را پس از حذف از پشته باز میگرداند.
- ()Peek: بدون حذف عنصر بالا پشته، آن را اعلام یا بازیابی میکند. گاهی میتوان به این متد «()Top» نیز گفت.

مثالهای عملی از ساختمان داده پشته در جاوا شامل معکوس کردن یک کلمه، بررسی صحت توالی پرانتزها، حل الگوریتم ماز (Maze) در جاوا، فراخوانی توابع تو در تو (Nested Function)، اجرای عملکرد برگشت در مرورگرها و سایر موارد هستند. کدهای زیر مثالی برای پیادهسازی پشته با استفاده از آرایه در جاوا است:
1package org.arpit.java2blog.datastructures;
2
3public class MyStack {
4 int size;
5 int arr[];
6 int top;
7
8 MyStack(int size) {
9 this.size = size;
10 this.arr = new int[size];
11 this.top = -1;
12 }
13
14 public void push(int element) {
15 if (!isFull()) {
16 top++;
17 arr[top] = element;
18 System.out.println("Pushed element:" + element);
19 } else {
20 System.out.println("Stack is full !");
21 }
22 }
23
24 public int pop() {
25 if (!isEmpty()) {
26 int topElement = top;
27 top--;
28 System.out.println("Popped element :" + arr[topElement]);
29 return arr[topElement];
30
31 } else {
32 System.out.println("Stack is empty !");
33 return -1;
34 }
35 }
36
37 public int peek() {
38 if(!this.isEmpty())
39 return arr[top];
40 else
41 {
42 System.out.println("Stack is Empty");
43 return -1;
44 }
45 }
46
47 public boolean isEmpty() {
48 return (top == -1);
49 }
50
51 public boolean isFull() {
52 return (size - 1 == top);
53 }
54
55 public static void main(String[] args) {
56 MyStack myStack = new MyStack(5);
57 myStack.pop();
58 System.out.println("=================");
59 myStack.push(100);
60 myStack.push(90);
61 myStack.push(10);
62 myStack.push(50);
63 System.out.println("=================");
64 myStack.pop();
65 myStack.pop();
66 myStack.pop();
67 System.out.println("=================");
68 }
69}خروجی کدهای فوق به صورت زیر است:
Stack is empty ! ================= Pushed element:100 Pushed element:90 Pushed element:10 Pushed element:50 ================= Popped element :50 Popped element :10 Popped element :90 =================
در ادامه مثالی برای پیادهسازی پشته با استفاده از لیست پیوندی ارائه شده است:
1package org.arpit.java2blog.datastructures;
2
3public class StackUsingLinkedList {
4 private Node head; // اولین گره
5
6 // .کلاس بعدی برای تعریف گره در لیست پیوندی ارائه شده است
7 private class Node {
8 int value;
9 Node next;
10 }
11
12 public StackUsingLinkedList() {
13 head = null;
14 }
15
16 // .برای شبیهسازی پشته، مقدار از ابتدای لیست حذف میشود
17 public int pop() throws LinkedListEmptyException {
18 if (head == null) {
19 throw new LinkedListEmptyException();
20 }
21 int value = head.value;
22 head = head.next;
23 return value;
24 }
25
26 // .برای شبیهسازی پشته، مقدار به ابتدای لیست اضافه میشود
27 public void push(int value) {
28 Node prevHead = head;
29 head = new Node();
30 head.value = value;
31 head.next = prevHead;
32 }
33
34 public static void main(String args[])
35 {
36 StackUsingLinkedList sll=new StackUsingLinkedList();
37 sll.push(200);
38 sll.push(150);
39 sll.push(80);
40 sll.push(90);
41 sll.push(600);
42 sll.push(175);
43 System.out.println("Removed element from LinkedList: "+sll.pop());
44 System.out.println("Removed element from LinkedList: "+sll.pop());
45 sll.push(100);
46 System.out.println("Removed element from LinkedList: "+sll.pop());
47 printList(sll.head);
48 }
49 public static void printList(Node head) {
50 Node temp = head;
51 while (temp != null) {
52 System.out.format("%d ", temp.value);
53 temp = temp.next;
54 }
55 System.out.println();
56 }
57}
58
59/**
60 * .اگر لیست پیوندی خالی باشد از کلاس زیر استفاده میشود
61 */
62
63class LinkedListEmptyException extends RuntimeException {
64 private static final long serialVersionUID = 1L;
65
66 public LinkedListEmptyException() {
67 super();
68 }
69
70 public LinkedListEmptyException(String message) {
71 super(message);
72 }
73}خروجی مثال فوق به صورت زیر است:
Removed element from LinkedList: 175 Removed element from LinkedList: 600 Removed element from LinkedList: 100 90 80 150 200
- مقالههای پیشنهادی:
در این بخش از این مقاله به بررسی ساختمان داده خطی پشته در جاوا پرداخته شد. اکنون در ادامه پیش از پرداختن به ساختمان داده خطی صف در جاوا، تعدادی از دورههای آموزش برنامه نویسی جاوا فرادرس معرفی شدهاند.
ساختمان داده صف در جاوا چیست؟
صف (Queue) نوع دیگری از ساختمان دادههای انتزاعی در جاوا به حساب میآید. بر خلاف پشته، صف مجموعهای از اشیا است که طبق اصل «اولین ورودی، اولین خروجی» یا «خروج به ترتیب ورود» (First In First Out | FIFO) درج و حذف اشیا را انجام میدهد.
عناصر را با اولویت زمانی میتوان در صف درج کرد، اما فقط عناصری را که بیشترین زمان در صف بودند را میتوان حذف کرد. در این ساختمان داده، درجها همیشه از «انتها» (Rear) و حذفها همیشه از «ابتدا» (Front) صف انجام میشوند. بخشی از ویژگیهای صف در ادامه ارائه شده است:
- ساختمان دادههای صف در جاوا اغلب به عنوان لیستهای «اولین ورودی، اولین خروجی» معرفی میشوند.
- دو متُد اساسی زیر در صف پشتیبانی میشوند:
- (e)Enqueue: افزودن عنصری مانند e به انتهای صف
- ()Dequeue: بازگرداندن اولین عنصر صف (عنصر جلوی صف) و حذف آن
در بخش بعدی مقاله «ساختمان داده در جاوا» به بررسی انواع گوناگون صفها در جاوا پرداخته شده است.
انواع ساختمان داده صف در جاوا
بر اساس نیاز برنامه مورد نظر، میتوان صفها را با شکلها و فرمهای گوناگونی استفاده کرد. دو نوع صف محبوب توسعه دهندگان در جاوا شامل صف حلقوی (Circular Queue) و صف دو طرفه (Double Ended Queues | Dequeue) میشوند.
در ادامه این بخش به معرفی کوتاهی از هر کدام از این صفها پرداخته شده است، ابتدا ساختمان داده صف حلقوی در جاوا بررسی میشود.
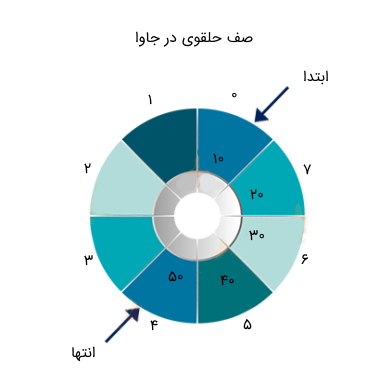
ساختمان داده صف حلقوی در جاوا چیست؟
ساختمان داده صفهای حلقوی به جای این که به صورت مستقیم پیادهسازی شوند، در یک مسیر دایرهای و حلقوی اجرا میشوند. این نوع از ساختمان داده مشکل فضاهای استفاده نشده در صفهای ساده و خطی که به عنوان آرایه پیادهسازی میشوند را برطرف میکند. تصویر زیر نمونهای از صفهای حلقوی را نشان میدهد.
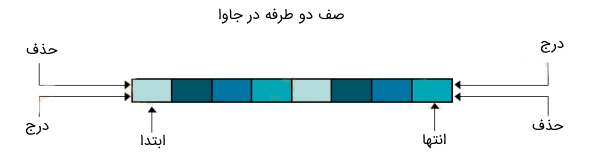
ساختمان داده صف دو طرفه در جاوا چیست؟
ساختمان داده صف دو طرفه در جاوا به صفی گفته میشود که عناصر را از هر دو طرف صف میتوان حذف و درج کرد، اما از وسط صف این کار را نمیتوان انجام داد. تصویر زیر نشان دهنده یک صف دو طرفه است.
در بخش بعدی برنامههایی مورد بررسی قرار میگیرند که در پیادهسازیهای خود از صف استفاده میکنند.
برنامههایی که از ساختمان داده صف در جاوا استفاده میکنند: ساختمان داده صف در جاوا دارای کاربردهای بسیاری است و در برنامههای زیادی از آنها استفاده میشود. در این بخش به بررسی برخی از برنامههایی پرداخته شده است که از این ساختمان دادهها در جاوا استفاده میکنند.
- ساختمان داده صف در پرس و جوهای تلفنی، درخواستهای رزرو، جریان ترافیک و سایر موارد استفاده میشود. برای مثال حتی ممکن است در تماس با تلفن پشتیبانیهای گویا و پیش از پاسخگویی کارشناس جمله «لطفا صبر کنید، شما در صف هستید.» اعلام شود.
- صف برای دسترسی به برخی از منابع مانند صف چاپگر، صف دیسک و سایر موارد استفاده میشود.
- از صف برای جست و جوی سطح اول (Breadth First Searching | BFS) در ساختمان دادههایی خاص مانند درختها و گرافها در جاوا استفاده میشود.
- این ساختمان داده در مدیریت زمانبندی فرآیندها در سیستم عاملهای چند وظیفهای (Multitasking Operating System) مانند الگوریتمهای زمانبندی (Scheduling Algorithm) «خدمت به ترتیب ورود» (First Come First Serve)، الگوریتم زمانبندی نوبت گردشی (Round Robin) و سایر موارد استفاده میشود.
- ساختمان داده صف در انتقال دادهها بین دو فرآیند به صورت نامتقارن (Asynchronous) مورد استفاده قرار میگیرد
- صف در زمانبندی پردازنده CPU کاربرد دارد.
- ساختمان داده صف در زمانبندی دیسک استفاده میشود.
این ساختمان داده در جاوا در سایر موقعیتها نیز مورد استفاده قرار میگیرد از جمله زمانی که منابع بین چندین کاربر به اشتراک گذاشته شده باشد. مثال زیر پیادهسازی برنامهای به حساب میآید که از ساختمان داده صف به وسیله آرایه استفاده کرده است:
1package org.arpit.java2blog.datastructures;
2
3public class MyQueue {
4
5 private int capacity;
6 int queueArr[];
7 int front;
8 int rear;
9 int currentSize = 0;
10
11 public MyQueue(int size) {
12 this.capacity = size;
13 front = 0;
14 rear = -1;
15 queueArr = new int[this.capacity];
16 }
17
18 /**
19 * متدی برای اضافه کردن عناصر به صف
20 */
21 public void enqueue(int data) {
22 if (isFull()) {
23 System.out.println("Queue is full!! Can not add more elements");
24 } else {
25 rear++;
26 if (rear == capacity - 1) {
27 rear = 0;
28 }
29 queueArr[rear] = data;
30 currentSize++;
31 System.out.println(data + " added to the queue");
32 }
33 }
34
35 /**
36 * .این متد عناصر را از ابتدای صف حذف میکند
37 */
38 public void dequeue() {
39 if (isEmpty()) {
40 System.out.println("Queue is empty!! Can not dequeue element");
41 } else {
42 front++;
43 if (front == capacity - 1) {
44 System.out.println(queueArr[front - 1] + " removed from the queue");
45 front = 0;
46 } else {
47 System.out.println(queueArr[front - 1] + " removed from the queue");
48 }
49 currentSize--;
50 }
51 }
52
53 /**
54 * .متدی که پر بودن صف را بررسی میکند
55 */
56 public boolean isFull() {
57 if (currentSize == capacity) {
58 return true;
59 }
60 return false;
61 }
62
63 /**
64 * .متدی که خالی بودن صف را بررسی میکند
65 */
66 public boolean isEmpty() {
67
68 if (currentSize == 0) {
69 return true;
70 }
71 return false;
72 }
73
74 public static void main(String a[]) {
75
76 MyQueue myQueue = new MyQueue(6);
77 myQueue.enqueue(1);
78 myQueue.dequeue();
79 myQueue.enqueue(30);
80 myQueue.enqueue(44);
81 myQueue.enqueue(32);
82 myQueue.dequeue();
83 myQueue.enqueue(98);
84 myQueue.dequeue();
85 myQueue.enqueue(70);
86 myQueue.enqueue(22);
87 myQueue.dequeue();
88 myQueue.enqueue(67);
89 myQueue.enqueue(23);
90 }
91}خروجی مثال فوق که پیادهسازی صف با استفاده از آرایه در جاوا را نشان میدهد، به صورت زیر است:
1 added to the queue 1 removed from the queue 30 added to the queue 44 added to the queue 32 added to the queue 30 removed from the queue 98 added to the queue 44 removed from the queue 70 added to the queue 22 added to the queue 32 removed from the queue 67 added to the queue 23 added to the queue
مثال بعدی ارائه شده، پیادهسازی برنامه به وسیله ساختمان داده صف و با استفاده از لیست پیوندی را نشان میدهد:
1package org.arpit.java2blog.datastructures;
2
3public class QueueUsingLinkedList
4{
5 private Node front, rear;
6 private int currentSize; // اندازه
7
8 // ساختمان داده گره
9 private class Node
10 {
11 int data;
12 Node next;
13 }
14
15 // سازنده
16 public QueueUsingLinkedList()
17 {
18 front = null;
19 rear = null;
20 currentSize = 0;
21 }
22
23 public boolean isEmpty()
24 {
25 return (currentSize == 0);
26 }
27
28 // .برای شبیهسازی صف، موردی از ابتدای لیست حذف میشود
29 public int dequeue()
30 {
31 int data = front.data;
32 front = front.next;
33 if (isEmpty())
34 {
35 rear = null;
36 }
37 currentSize--;
38 System.out.println(data+ " removed from the queue");
39 return data;
40 }
41
42 // .برای شبیهسازی صف دادهای به انتهای صف اضافه میشود
43 public void enqueue(int data)
44 {
45 Node oldRear = rear;
46 rear = new Node();
47 rear.data = data;
48 rear.next = null;
49 if (isEmpty())
50 {
51 front = rear;
52 }
53 else
54 {
55 oldRear.next = rear;
56 }
57 currentSize++;
58 System.out.println(data+ " added to the queue");
59 }
60 public static void main(String a[]){
61
62 QueueUsingLinkedList queueUsingLinkedList = new QueueUsingLinkedList();
63 queueUsingLinkedList.enqueue(60);
64 queueUsingLinkedList.dequeue();
65 queueUsingLinkedList.enqueue(10);
66 queueUsingLinkedList.enqueue(20);
67 queueUsingLinkedList.enqueue(40);
68 queueUsingLinkedList.dequeue();
69 queueUsingLinkedList.enqueue(70);
70 queueUsingLinkedList.dequeue();
71 queueUsingLinkedList.enqueue(80);
72 queueUsingLinkedList.enqueue(100);
73 queueUsingLinkedList.dequeue();
74 queueUsingLinkedList.enqueue(150);
75 queueUsingLinkedList.enqueue(50);
76 }
77}خروجی برنامه فوق که مثالی برای پیادهسازی برنامه به وسیله ساختمان داده صف با لیست پیوندی است، به صورت زیر نمایش داده میشود:
60 added to the queue 60 removed from the queue 10 added to the queue 20 added to the queue 40 added to the queue 10 removed from the queue 70 added to the queue 20 removed from the queue 80 added to the queue 100 added to the queue 40 removed from the queue 150 added to the queue 50 added to the queue
بخش بعدی مقاله «ساختمان داده در جاوا» به بررسی ساختمان دادههای غیر خطی و سلسله مراتبی در جاوا اختصاص داده شده است.
ساختمان داده غیر خطی در جاوا چیست؟
ساختمان داده غیر خطی یا سلسله مراتبی در جاوا، برای حذف و درج عناصر دارای ترتیب خاصی به صورت خطی ندارد. ساختمان دادههای غیر خطی، ساختمان دادههایی چند سطحی (Multilevel Data Structure) به حساب میآیند.
در این بخش به بررسی برخی از مهمترین این نوع ساختمان دادهها در جاوا پرداخته میشود. ابتدا در بخش بعدی ساختمان داده درخت دودویی در جاوا مورد بررسی قرار میگیرد.
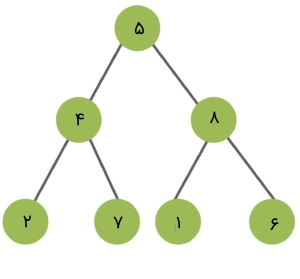
ساختمان داده درخت دودویی در جاوا چیست؟
درخت دودویی یا همان باینری (Binary Tree) یک ساختمان داده درختی غیر خطی و سلسله مراتبی است که هر گره آن دارای حداکثر دو فرزند است که با نامهای فرزند سمت چپ (Left Child) و فرزند سمت راست (Right Child) شناخته میشوند.
هر درخت باینری دودویی دارای گروهی از گرهها به صورت زیر است:
- گره ریشه (Root Node): این ریشه بالاترین ریشه درخت است و گاهی به عنوان ریشه اصلی نیز شناخته میشود زیرا همه ریشههای دیگر از این ریشه نشأت میگیرند و به آن متصل هستند.
- زیر درخت سمت چپ (Left Sub Tree): یک درخت باینری است که در سمت چپ درخت باینری اصلی ایجاد میشود.
- زیر درخت سمت راست (Right Sub Tree): زیر درخت سمت راست نیز خودش یک درخت باینری به حساب میآید.
در ادامه این بخش، ویژگیهای ساختمان داده درخت باینری در جاوا ارائه شده است:
- درخت باینری با دو روش به صورت زیر پیمایش میشود:
- الگوریتم پیمایش عمق اول (Depth First Traversal): این نوع پیمایش شامل پیمایش «In Order» یا همان میانوندی به صورت «راست - ریشه - چپ»، پیمایش «Pre Order» یا همان پیشوندی به صورت «راست - چپ - ریشه» و پیمایش پسوندی یا همان «Post Order» به صورت «ریشه - راست - چپ» است.
- الگوریتم پیمایش سطح اول (Breadth First Traversal): در این نوع از الگوریتمها پیمایش به ترتیب سطح انجام میشود. (Level Order Traversal)
- پیچیدگی زمانی (Time Complexity) پیمایش درخت «(n)O» است.
- حداکثر تعداد گرهها در هر سطح است.
کاربردهای ساختمان داده درخت دودویی در جاوا چه هستند؟
کاربردهای این ساختمان داده در جاوا شامل موارد زیر میشوند:
- ساختمان داده درخت دودویی در بسیاری از برنامههای جست و جویی استفاده میشود که دادهها همواره در حال ورود و خروج هستند.
- درخت دودویی به عنوان یک جریان کار در ترکیب تصاویر دیجیتال برای جلوههای بصری (Visual Effect) مورد استفاده قرار میگیرد.
- میتوان گفت تقریباً از درخت دودویی جاوا در هر مسیریاب (Router) با پهنای باند بالا (High Bandwidth) برای ذخیره جدولهای مسیریاب استفاده میشود.
- این ساختمان داده در شبکههای بیسیم (Wireless Network) و تخصیص حافظه (Memory Allocation) استفاده میشود.
- در الگوریتمهای فشردهسازی (Compression Algorithm) و بسیاری از الگوریتمهای دیگر نیز استفاده میشود.
در ادامه مثالی برای درک بهتر ساختمان داده درخت دودویی یا باینری ارائه شده است:
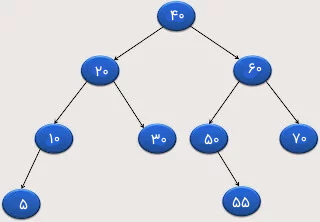
1package org.arpit.java2blog.datastructures;
2
3import java.util.Stack;
4
5public class BinaryTree {
6
7 public static class Node
8 {
9 int data;
10 Node left;
11 Node right;
12 Node(int data)
13 {
14 this.data=data;
15 }
16 }
17
18 // راه حل بازگشتی
19 public void preorder(Node root) {
20 if(root != null) {
21 //Pre order traversal
22 System.out.printf("%d ",root.data);
23 preorder(root.left);
24 preorder(root.right);
25 }
26 }
27
28 // راه حل تکراری
29 public void preorderIter(Node root) {
30
31 if(root == null)
32 return;
33
34 Stack<Node> s = new Stack<Node>();
35 s.push(root);
36
37 while(!s.empty()){
38
39 Node n = s.pop();
40 System.out.printf("%s ",n.data);
41
42 if(n.right != null){
43 s.push(n.right);
44 }
45 if(n.left != null){
46 s.push(n.left);
47 }
48
49 }
50
51 }
52
53 public static void main(String[] args)
54 {
55 BinaryTree bi=new BinaryTree();
56 // ایجاد ساختمان داده درخت باینری
57 Node rootNode=createBinaryTree();
58 System.out.println("Using Recursive solution:");
59
60 bi.preorder(rootNode);
61
62 System.out.println();
63 System.out.println("-------------------------");
64 System.out.println("Using Iterative solution:");
65
66 bi.preorderIter(rootNode);
67 }
68
69 public static Node createBinaryTree()
70 {
71
72 Node rootNode =new Node(30);
73 Node node20=new Node(50);
74 Node node10=new Node(60);
75 Node node30=new Node(80);
76 Node node60=new Node(90);
77 Node node50=new Node(100);
78 Node node70=new Node(110);
79
80 rootNode.left=node20;
81 rootNode.right=node60;
82
83 node20.left=node10;
84 node20.right=node30;
85
86 node60.left=node50;
87 node60.right=node70;
88
89 return rootNode;
90 }
91}خروجی مثال درخت باینری ارائه شده به صورت زیر نمایش داده میشود:
Using Recursive solution: 30 50 60 80 90 100 110 ————————- Using Iterative solution: 30 50 60 80 90 100 110
در بخش بعدی مقاله «ساختمان داده در جاوا» به بررسی ساختمان داده درخت جست و جوی دودویی پرداخته شده است.
ساختمان داده درخت جست و جوی دودویی در جاوا چیست؟
ساختمان داده درخت جست و جوی دودویی یا باینری (Binary Search Tree | BST) یک نوع خاصی از ساختمان داده درخت دودویی در جاوا به حساب میآید که دارای ویژگیهای زیر است:
- در درخت جست و جوی دودویی گرههایی که کوچکتر از ریشه هستند در زیر درخت سمت چپ قرار میگیرند.
- در این ساختمان داده در جاوا گرههایی که بزرگتر از ریشه هستند در زیر درخت سمت راست قرار میگیرند.
- درخت جست و جوی دودویی نباید گره تکراری داشته باشد.
- زیر درختهای چپ و راست هر دو باید به تنهایی یک درخت جست و جوی دودویی باشند.
در ادامه این بخش برای درک بهتر ساختمان داده درخت جستجوی باینری در جاوا مثالی برای آن ارائه شده است: (شکل این مثال با مثال بخش درخت دودویی تفاوتی ندارد.)
1package org.arpit.java2blog.datastructures;
2
3public class MyBinarySearchTree {
4 public static class Node
5 {
6 int data;
7 Node left;
8 Node right;
9 Node(int data)
10 {
11 this.data=data;
12 }
13 }
14
15 public static boolean search(Node root, Node nodeToBeSearched)
16 {
17 if(root==null)
18 return false;
19 if(root.data== nodeToBeSearched.data)
20 {
21 return true;
22 }
23 boolean result=false;
24
25 if(root.data > nodeToBeSearched.data)
26 result=search(root.left,nodeToBeSearched);
27 else if(root.data < nodeToBeSearched.data)
28 result= search(root.right,nodeToBeSearched);
29
30 return result;
31 }
32
33 public static Node insert(Node root, Node nodeToBeInserted)
34 { if(root==null) {
35 root=nodeToBeInserted; return root;
36 } if(root.data > nodeToBeInserted.data)
37 {
38 if(root.left==null)
39 root.left=nodeToBeInserted;
40 else
41 insert(root.left,nodeToBeInserted);
42 }
43 else if(root.data < nodeToBeInserted.data)
44 if(root.right==null)
45 root.right=nodeToBeInserted;
46 else
47 insert(root.right,nodeToBeInserted);
48 return root;
49 }
50
51 public static void inOrder(Node root)
52 {
53 if(root==null)
54 return;
55 inOrder(root.left);
56 System.out.print(root.data+" ");
57 inOrder(root.right);
58 }
59 public static void main(String[] args)
60 {
61 // ایجاد درخت جستوجوی باینری
62 Node rootNode=createBinarySearchTree();
63 Node node55=new Node(55);
64 boolean result=search(rootNode,node55);
65 System.out.println("Searching for node 55 : "+result);
66 System.out.println("---------------------------");
67 Node node13=new Node(13);
68 Node root=insert(rootNode,node13);
69 System.out.println("Inorder traversal of binary tree after adding 13:");
70 inOrder(root);
71
72 }
73
74 public static Node createBinarySearchTree()
75 {
76 Node rNode =new Node(40);
77 Node node20=new Node(20);
78 Node node10=new Node(10);
79 Node node30=new Node(30);
80 Node node60=new Node(60);
81 Node node50=new Node(50);
82 Node node70=new Node(70);
83 Node node5=new Node(5);
84 Node node55=new Node(55);
85
86 insert(null,rNode);
87 insert(rNode,node20);
88 insert(rNode,node10);
89 insert(rNode,node30);
90 insert(rNode,node60);
91 insert(rNode,node50);
92 insert(rNode,node70);
93 insert(rNode,node5);
94 insert(rNode,node55);
95 return rNode;
96 }
97
98}خروجی مثال فوق به صورت زیر است:
Searching for node 55 : true ————————— Inorder traversal of binary tree after adding 13: 5 10 13 20 30 40 50 55 60 70
در بخش بعدی این مقاله به بررسی و معرفی ساختمان داده درخت پیشوندی پرداخته شده است.
ساختمان داده درخت پیشوندی در جاوا چیست؟
ساختمان داده درخت پیشوندی (Trie Tree)، ساختمان دادهای است که به گونهای دادهها را ذخیرهسازی میکند تا بتوان آنها را به راحتی بازیابی کرد. برای مثال این ساختمان داده برای پیادهسازی «Dictionary» مورد استفاده قرار میگیرد. در ادامه مثالی در رابطه با پیادهسازی ساختمان داده درخت پیشوندی مشاهده میشود.
در این مثال کلمات در درخت پیشوندی قرار گرفتهاند. فرض میشود که قرار است کلمات do ،deal ،dear ،he ،hen ،heat و سایر موارد وارد شوند.
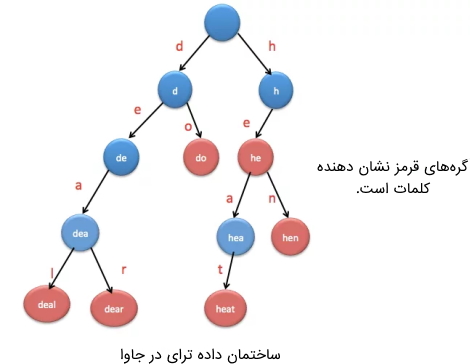
1package org.arpit.java2blog.datastructures;
2
3/*
4 * برنامه جاوا برای پیادهسازی درخت ترای
5 */
6
7import java.util.*;
8
9class TrieNode
10{
11 char data;
12 boolean isEnd;
13 int count;
14 LinkedList<TrieNode> childList;
15
16 /* سازنده */
17 public TrieNode(char c)
18 {
19 childList = new LinkedList();
20 isEnd = false;
21 data = c;
22 count = 0;
23 }
24 public TrieNode getChild(char c)
25 {
26 if (childList != null)
27 for (TrieNode eachChild : childList)
28 if (eachChild.data == c)
29 return eachChild;
30 return null;
31 }
32}
33
34public class Trie
35{
36 private TrieNode root;
37
38 /* سازنده */
39 public Trie()
40 {
41 root = new TrieNode(' ');
42 }
43 /* متد درج ترای از درخت ترای*/
44 public void insert(String word)
45 {
46 if (search(word) == true)
47 return;
48 TrieNode tempCurr = root;
49 for (char ch : word.toCharArray() )
50 {
51 TrieNode child = tempCurr.getChild(ch);
52 if (child != null)
53 tempCurr = child;
54 else
55 {
56 // .اگر فرزند وجود نداشت به لیست اضافه میشود
57 tempCurr.childList.add(new TrieNode(ch));
58 tempCurr = tempCurr.getChild(ch);
59 }
60 tempCurr.count++;
61 }
62 tempCurr.isEnd = true;
63 }
64 /* متد برای جستوجوی کلمات در درخت ترای*/
65 public boolean search(String word)
66 {
67 TrieNode tempCurr = root;
68 for (char ch : word.toCharArray() )
69 {
70 if (tempCurr.getChild(ch) == null)
71 return false;
72 else
73 tempCurr = tempCurr.getChild(ch);
74 }
75 if (tempCurr.isEnd == true)
76 return true;
77 return false;
78 }
79 /* متد برای حذف کلمات از درخت ترای*/
80 public void remove(String word)
81 {
82 if (search(word) == false)
83 {
84 System.out.println(word +" does not present in trien");
85 return;
86 }
87 TrieNode tempCurr = root;
88 for (char ch : word.toCharArray())
89 {
90 TrieNode child = tempCurr.getChild(ch);
91 if (child.count == 1)
92 {
93 tempCurr.childList.remove(child);
94 return;
95 }
96 else
97 {
98 child.count--;
99 tempCurr = child;
100 }
101 }
102 tempCurr.isEnd = false;
103 }
104
105 public static void displayWordsInTrie(TrieNode root, String str)
106 {
107 TrieNode tempCurr = root;
108 if(root.childList==null || root.childList.size()==0)
109 return;
110 Iterator iter=tempCurr.childList.iterator();
111 while(iter.hasNext())
112 {
113 TrieNode trieNode= (TrieNode) iter.next();
114 str+=trieNode.data;
115 displayWordsInTrie(trieNode,str);
116 if(trieNode.isEnd==true)
117 {
118 System.out.print(" "+str);
119 str=str.substring(0,str.length()-1);
120 }
121 else
122 {
123 str=str.substring(0,str.length()-1);
124 }
125 }
126
127 }
128 public static void main(String[] args)
129 {
130 Trie t = new Trie();
131 t.insert("apple");
132 t.insert("ape");
133 t.insert("goat");
134 t.insert("goa");
135 t.insert("apt");
136
137 System.out.println("go present in trie : "+t.search("go"));
138 System.out.println("goa present in trie : "+t.search("goa"));
139 System.out.println("appl present in trie : "+t.search("ape"));
140 System.out.println("========================");
141 System.out.println("Displaying all word present in trie : ");
142 displayWordsInTrie(t.root,"");
143 }
144}خروجی مثال پیادهسازی ساختمان داده درخت پیشوندی فوق به صورت زیر نشان داده میشود:
go present in trie : false goa present in trie : true appl present in trie : true ======================== Displaying all word present in trie : apple ape apt goat goa
بخش بعدی این مقاله به شرح ساختمان داده هرمی دودویی در جاوا اختصاص دارد.
ساختمان داده هرمی دودویی در جاوا چیست؟
هرمی دودویی یا همان باینری (Binary Heap) یک درخت دودویی کامل است که ویژگیهای هرمی را پاسخ میدهد.
به عبارت دیگر، نوع متفاوتی از درخت باینری با ویژگیهای زیر است:
- هرمی یک درخت باینری کامل است. به درختی کامل گفته میشود که همه سطوح آن کامل باشند، فقط گاهی امکان دارد که عمیقترین سطح آن کامل نباشد. ویژگیهای درخت باینری هرمی آن را برای ذخیره در یک آرایه مناسب میکند.
- باینری هرمی به صورت هرمی مینیمم (Min Heap) و هرمی ماکسیمم (Max Heap) دارای ویژگیهای زیر است:
- هرمی دودویی مینیمم: برای هر گرهای در این هرمی، مقادیر گرهها کمتر و مساوی مقادیر گرههای فرزندان است.
- هرمی دودویی ماکسیمم: برای هر گرهای در این نوع از هرمیها، مقادیر هر گره بزرگتر و مساوی مقادیر فرزندان آن است.
برنامههای محبوب هرمی دودویی شامل پیادهسازی مؤثر و کارآمد صفهای اولویت (Priority Queue)، پیدا کردن کوچکترین یا بزرگترین عنصر در آرایهها با بهترین کیفیت و سایر موارد میشوند. در ادامه برای درک بهتر موضوع ساختمان داده هرمی در جاوا مثالی برای هرمی مینیمم ارائه شده است:
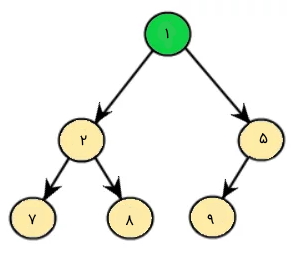
1package org.arpit.java2blog.datastructures;
2
3import java.util.Arrays;
4public class MinHeap
5{
6 int Heap[];
7 int size;
8 int capacity;
9
10 public MinHeap(int size)
11 {
12 this.capacity = size;
13 this.size = 0;
14 Heap = new int[size];
15 }
16
17 int parent(int i)
18 {
19 return (i - 1)/2; // .ام را برمیگرداند i اندیس گره والد
20 }
21
22 int leftChild(int i)
23 {
24 return (2 * i) + 1; // .اندیس فرزند سمت چپ را برمیگرداند
25 }
26
27 int rightChild(int i)
28 {
29 return (2 * i) + 2; // .اندیس فرزند سمت راست را برمیگرداند
30 }
31
32 boolean isLeaf(int i) // امین گره، گره برگ است یا خیر i بررسی میکند که آیا
33 {
34 if (rightChild(i) >= size || leftChild(i) >= size)
35 return true;
36
37 return false;
38 }
39
40 /* متد درج گره در ساختمان داده مین هیپ در جاوا
41
42 */
43 void insert(int data)
44 {
45 if (size >= capacity)
46 return;
47
48 Heap[size] = data;
49 int tempCurr = size;
50
51 while (Heap[tempCurr] < Heap[parent(tempCurr)])
52 {
53 swap(tempCurr, parent(tempCurr));
54 tempCurr = parent(tempCurr);
55 }
56 size++;
57 }
58
59 // حذف و برگرداندن عناصر مینیمم یا ریشه هیپ
60 int extractMinimum()
61 {
62 int min = Heap[0];
63 Heap[0] = Heap[--size];
64 minHeapify(0);
65 System.out.print("\nThe Min Heap after Removing node is :");
66
67 for(int i=0;i<size;i++)
68 System.out.print(Heap[i]+" ");
69
70 System.out.println();
71 return min;
72 }
73
74 // فقط برگرداندن مقادیر مینیمم و ریشه
75 int getMinimum()
76 {
77 int min=Heap[0];
78 return min;
79 }
80
81 // (Heapify) هیپ کردن گره iام
82 void minHeapify(int i)
83 {
84
85 // .اگر گره، یک گره غیر برگ باشد و هر یک از فرزندان آن کوچکتر باشند
86 if(!isLeaf(i))
87 {
88 if(Heap[i] > Heap[leftChild(i)] || Heap[i] > Heap[rightChild(i)])
89 {
90 if(Heap[leftChild(i)] < Heap[rightChild(i)])
91 {
92 swap(i, leftChild(i));
93 minHeapify(leftChild(i));
94 }
95 else
96 {
97 swap(i, rightChild(i));
98 minHeapify(rightChild(i));
99 }
100
101 }
102 }
103
104 }
105
106 // minHeapify ساخت مین هیپ با استفاده از
107 public void minHeap()
108 {
109 // .تا زمانی که «اندازه/۲» باعث شود گرههای والد تا آن اندیس وجود داشته باشند فراخوانی انجام میشود
110 for (int i = (size-1)/2; i >= 0; i--)
111 {
112 minHeapify(i);
113 }
114 }
115
116 // چاپ محتوای هیپ
117 public void printHeap()
118 {
119 for (int i = 0; i < (size / 2); i++)
120 {
121 if(i==0)
122 System.out.print("Root : "+ Heap[i]);
123 else
124 System.out.print("Parent : " + Heap[i]);
125
126 if (leftChild(i) < size)
127 System.out.print(" Left : " + Heap[leftChild(i)]);
128
129 if (rightChild(i) < size)
130 System.out.print(" Right : " + Heap[rightChild(i)]);
131
132 System.out.println();
133 }
134 }
135
136 // تعویض دو گره از هیپ
137 void swap(int x, int y)
138 {
139 int temp;
140 temp = Heap[x];
141 Heap[x] = Heap[y];
142 Heap[y] = temp;
143 }
144
145 // کدهایی برای تست روشهای فوق
146 public static void main(String[] args)
147 {
148
149 // ایجاد یک مین هیپ با ظرفیت ۶
150 MinHeap heap = new MinHeap(6);
151
152 heap.insert(100);
153 heap.insert(200);
154 heap.insert(500);
155 heap.insert(700);
156 heap.insert(800);
157 heap.insert(900);
158
159 // ساخت مین هیپ
160 heap.minHeap();
161 System.out.println("The Min Heap is : "+ Arrays.toString(heap.Heap));
162
163 // انجام مینیمم عملیات
164 System.out.println("\nThe Min Value in the heap : " + heap.getMinimum());
165 System.out.println();
166
167 heap.printHeap();
168
169 // استخراج مینیمم عملیات
170 System.out.println("Extracted Minimum Node in the heap : " + heap.extractMinimum());
171 System.out.println();
172
173 // .در نهایت هیپ برای بررسی موارد حذف شده، بررسی میشود
174 heap.printHeap();
175
176 }
177}خروجی مثال ساختمان داده مین هرمی فوق به صورت زیر است:
The Min Heap is : [100, 200, 500, 700, 800, 900] The Min Value in the heap : 100 Root : 100 Left : 200 Right : 500 Parent : 200 Left : 700 Right : 800 Parent : 500 Left : 900 The Min Heap after Removing node is :200 700 500 900 800 Extracted Minimum Node in the heap : 100 Root : 200 Left : 700 Right : 500 Parent : 700 Left : 900 Right : 800
در بخش بعدی مقاله «ساختمان داده در جاوا» به بررسی ساختمان داده گراف در جاوا پرداخته شده است.
ساختمان داده گراف در جاوا چیست؟
گراف یک ساختمان داده غیر خطی در جاوا است و مؤلفههایی که در ادامه ارائه شدهاند، آن را تعریف میکنند:
- گراف شامل مجموعهای از تعداد محدودی از رئوس (Vertice) است که به عنوان گره یا همان «Node» شناخته میشوند.
- ساختمان داده گراف دارای یالی (Edge) با مجموعه محدودی از جفتهای مرتب به شکل (e, v) است.
- V نشان دهنده تعداد رئوس است.
- E نشان دهنده تعداد یالها است.
در بخش بعدی مقاله به بررسی انواع گرافها و طبقهبندی انواع آنها پرداخته شده است.
انواع طبقهبندیهای ساختمان داده گراف در جاوا چگونه است؟
ساختمان داده گراف در جاوا بر اساس پارامترهای آن به دو دسته «گراف مسیر» (Direction Graph) و «گراف وزن» (Weight Graph) طبقهبندی میشود که در این بخش به بررسی هر کدام از آنها پرداخته میشود. ابتدا ساختمان داده گراف مسیر مورد بررسی قرار میگیرد.
ساختمان داده گراف مسیر در جاوا چیست؟
در ساختمان داده گراف مسیر در جاوا، گرافها به دو دسته گراف جهتدار (Directed Graph) و گراف بدون جهت (Undirected Graph) تقسیم میشوند. در بخش بعدی این مقاله، گراف جهتدار بررسی شده است.
گراف جهتدار در جاوا چیست؟
گراف جهتدار مجموعهای از گرهها یا رئوس متصل به یکدیگر است که در آن همه یالها دارای جهتی از یک رأس به رأس دیگر هستند. تصویر زیر نمونه سادهای از این نوع گراف به حساب میآید.
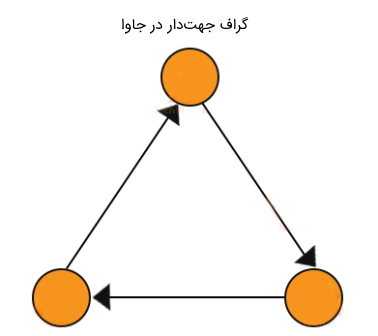
- مقاله پیشنهادی: برنامه تشخیص وجود دور در گراف جهت دار — راهنمای کاربردی
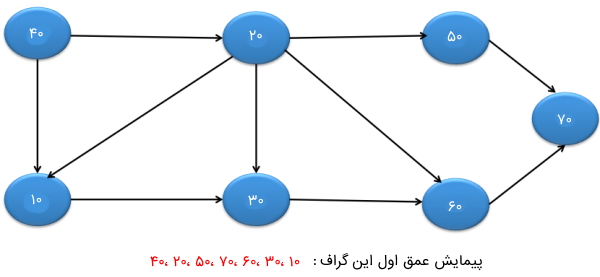
حال در این بخش برای درک بهتر گراف در جاوا و آشنایی با کدهای برنامه نویسی گراف در طراحی گرافها مثالی از یک گراف جهتدار با استفاده از الگوریتم پیمایش جست و جوی عمق اول (Depth First Search | DFS) ارائه شده است:
1package org.arpit.java2blog.datastructures;
2import java.util.ArrayList;
3import java.util.List;
4import java.util.Stack;
5
6public class GraphMain
7{
8
9 static class Node
10 {
11 int data;
12 boolean visited;
13 List<Node> neighbours;
14
15 Node(int data)
16 {
17 this.data=data;
18 this.neighbours=new ArrayList<>();
19
20 }
21 public void addneighbours(Node neighbourNode)
22 {
23 this.neighbours.add(neighbourNode);
24 }
25 public List<Node> getNeighbours() {
26 return neighbours;
27 }
28 public void setNeighbours(List<Node> neighbours) {
29 this.neighbours = neighbours;
30 }
31 }
32
33 // الگوریتم پیمایش عمق اول بازگشتی
34 public void recursiveDFS(Node node)
35 {
36 System.out.print(node.data + " ");
37 List<Node> neighbours=node.getNeighbours();
38 node.visited=true;
39 for (int i = 0; i < neighbours.size(); i++) {
40 Node n=neighbours.get(i);
41 if(n!=null && !n.visited)
42 {
43 recursiveDFS(n);
44 }
45 }
46 }
47
48 // الگوریتم پیمایش عمق اول با استفاده از پشته
49 public void iterativeDFS(Node node)
50 {
51 Stack<Node> stack=new Stack<Node>();
52 stack.add(node);
53 while (!stack.isEmpty())
54 {
55 Node element=stack.pop();
56 if(!element.visited)
57 {
58 System.out.print(element.data + " ");
59 element.visited=true;
60 }
61
62 List<Node> neighbours=element.getNeighbours();
63 for (int i = 0; i < neighbours.size(); i++) {
64 Node n=neighbours.get(i);
65 if(n!=null && !n.visited)
66 {
67 stack.add(n);
68 }
69 }
70 }
71 }
72
73 public static void main(String arg[])
74 {
75
76 Node node40 =new Node(40);
77 Node node10 =new Node(10);
78 Node node20 =new Node(20);
79 Node node30 =new Node(30);
80 Node node60 =new Node(60);
81 Node node50 =new Node(50);
82 Node node70 =new Node(70);
83
84 node40.addneighbours(node10);
85 node40.addneighbours(node20);
86 node10.addneighbours(node30);
87 node20.addneighbours(node10);
88 node20.addneighbours(node30);
89 node20.addneighbours(node60);
90 node20.addneighbours(node50);
91 node30.addneighbours(node60);
92 node60.addneighbours(node70);
93 node50.addneighbours(node70);
94
95 GraphMain gm = new GraphMain();
96
97 System.out.println("Iterative DFS traversal ");
98 gm.iterativeDFS(node40);
99
100 System.out.println();
101
102 // بازنشانی گرهها
103 node40.visited=false;
104 node10.visited=false;
105 node20.visited=false;
106 node30.visited=false;
107 node60.visited=false;
108 node50.visited=false;
109 node70.visited=false;
110
111 System.out.println("Recursive DFS traversal ");
112 gm.recursiveDFS(node40);
113 }
114}خروجی مثال فوق به صورت زیر است:
Iterative DFS traversal 40 20 50 70 60 30 10 Recursive DFS traversal 40 10 30 60 70 20 50
در بخش بعدی مقاله «ساختمان داده در جاوا» به معرفی گراف بدون جهت پرداخته شده است.
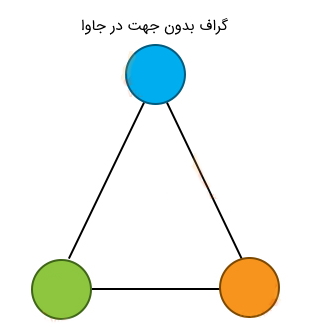
گراف بدون جهت در جاوا چیست؟
گراف بدون جهت مجموعهای از گرهها یا رئوس متصل به یکدیگر است که دارای مسیر جهتداری از یک یال به یال دیگر نیستند. تصویر زیر نمونه سادهای از گراف بدون جهت را نشان میدهد. در بخش بعدی مقاله به بررسی گراف وزن پرداخته شده است.
ساختمان داده گراف وزندار در جاوا چیست؟
بر پایه وزنها، گراف میتواند به دو دسته گراف وزندار (Weighted Graph) و گراف بدون وزن (Unweighted Graph) تقسیم شود. در ادامه این بخش به بررسی دو نوع گراف مذکور پرداخته میشود. ابتدا بخش بعدی به معرفی گراف وزندار اختصاص داده شده است.
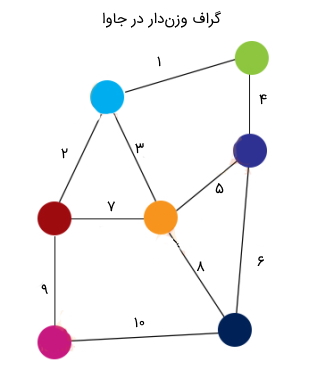
گراف وزندار در جاوا چیست؟
ساختمان داده گراف وزندار در جاوا، گرافی است که هر یال آن دارای وزن باشد. این گراف نوع خاصی از گراف برچسبدار (Labeled Graph) به حساب میآید. در تصویر زیر نمونهای از یک گراف وزندار مشاهده میشود. در بخش بعدی این مقاله، گراف بدون وزن شرح داده شده است.
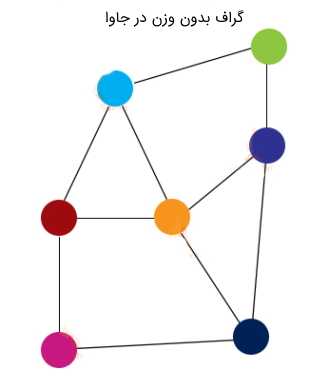
گراف بدون وزن در جاوا چیست؟
در ساختمان داده گراف بدون وزن هیچ وزنی برای یالهای آن اختصاص داده نشده است. در تصویر زیر یک گراف بدون وزن ساده نشان داده شده است.
بخش بعدی این مقاله به معرفی ساختمان داده مجموعه اختصاص دارد.
ساختمان داده مجموعه در جاوا چیست؟
مجموعه (Set) ساختمان دادهای خاص است که از مقادیر تکراری (Duplicate Value) استفاده نمیکند. این ساختمان داده در جاوا معمولاً برای ذخیره عناصر منحصربهفرد مانند شناسه کاربری یکتا (ID) مورد استفاده قرار میگیرد.
پیادهسازیهای زیادی از ساختمان داده مجموعه در جاوا وجود دارند که برخی از آنها شامل مجموعه درهمسازی پیوندی (Linked Hash Set)، مجموعه درهمسازی (Hash Set) و مجموعه درخت (Tree Set) میشوند که این ساختمان دادهها در جاوا توسط مجموعه API جاوا (Java Collection API) ارائه شدهاند. در تصویر زیر نمونهای از ساختمان داده مجموعه در جاوا مشاهده میشود.
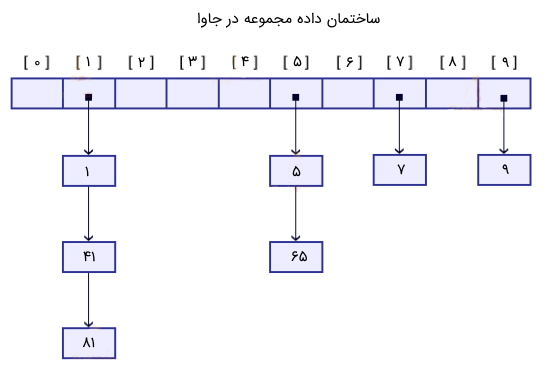
در بخش بعدی این مقاله جدول درهمسازی در جاوا بررسی شده است.
ساختمان داده جدول درهم سازی در جاوا چیست؟
فرض میشود که شئی وجود دارد و کلیدی به آن اختصاص داده میشود تا جست و جو را آسان کند. برای ذخیره کلید و مقدار به صورت جفت، میتوان از یک آرایه ساده مانند یک ساختمان داده در جاوا استفاده کرد که در آن کلیدها (اعداد صحیح) میتوانند مستقیماً به عنوان اندیسی برای ذخیره مقادیر دادهها استفاده شوند. با این حال، در مواردی که کلید بسیار بزرگ است و به عنوان یک اندیس به طور مستقیم نمیتوان از آن استفاده کرد از روش جدول درهمسازی (Hash Table) استفاده میشود.
در روشهای درهمسازی، کلیدهای بزرگ به وسیله تابع درهمسازی (Hash Function) به کلیدهای کوچک تبدیل میشوند، سپس مقادیر ایجاد شده در ساختمان دادهای به نام جدول درهمسازی ذخیره شده است. جدول درهمسازی یک ساختمان داده به حساب میآید که دیکشنری دادهها با نوع انتزاعی (ADT) را پیادهسازی میکند. این ساختمان داده میتواند کلیدهای منحصر به فرد را به مقادیر نگاشت کند.
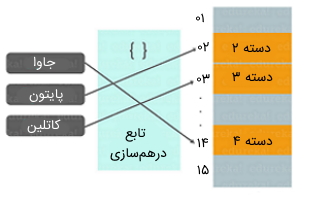
به صورت کلی، ساختمان داده جدول درهمسازی دارای دو مؤلفه اصلی زیر است:
- آرایه سطلی (Bucket Array): آرایه سطلی برای تابع درهمسازی یک آرایه A با سایز N، آرایهای است که هر سلول آن یک سطل یا «Bucket» نامیده میشود. این آرایه مجموعهای از جفتهای کلید و مقادیر است. عدد صحیح N ظرفیت آرایه A را مشخص میکند.
- تابع درهمسازی: هر تابعی که کلید k را به عدد صحیحی در بازه [N-1 و 0] نگاشت کند، تابع درهمسازی نامیده میشود. N در این بازه ظرفیت آرایه سطلی را نشان میدهد.
زمانی که اشیا در جدولهای درهمسازی قرار میگیرند، امکان دارد که اشیا گوناگون دارای کد درهمسازی یکسانی باشند. به این مسئله تصادم یا برخورد (Collision) گفته میشود. برای جلوگیری از تصادم، روشهایی مانند آدرسدهی زنجیرهای (Chain) یا باز (Open) وجود دارند.
به این ترتیب، در این مقاله سعی شد تا حد امکان به طور جامع به این سوال پاسخ داده شود که ساختمان داده در جاوا چیست و به انواع گوناگون ساختمان دادهها در جاوا نیز پرداخته شد. اکنون در بخش پایانی این مقاله، برای آشنایی بیشتر و آموزش جامعتر ساختمان داده در جاوا ، آن دسته از دورههای فرادرس که بیشترین ارتباط را با ساختمان دادهها در جاوا دارند به علاقهمندان معرفی شدهاند.
جمعبندی
در این مقاله سعی شد تا حد امکان به طور جامع به ساختمان داده در جاوا و انواع گوناگون آن پرداخته شود. همچنین، برخی از ساختمان دادههای مهم در جاوا از جمله آرایه، لیست پیوندی، پشته، صف، گراف، جدول درهمسازی و مجموعه همراه با انواع، پیادهسازی و مثال مورد بررسی قرار گرفتند.
مشخص است که یادگیری این موضوع در جاوا پیشرفت زیادی در کدنویسی جاوا برای برنامه نویسان به ارمغان میآورد. در این مقاله علاوه بر معرفی انواع ساختمان دادهها در جاوا، کدهایی برای پیادهسازی برخی از آنها ارائه شده است که سعی در پوشش دادن اکثر مطالب هر ساختمان داده را دارند. امید است این مقاله مفید واقع شود.













سلام.
عالی
آموزش ساختمان داده همراه با پیاده سازی در سی پلاس پلاس در فرادرس هم شامل پیاده سازی است.