درخت جستجوی دودویی (BST) – ساختار داده و الگوریتم ها

درخت نشان دهنده گره‌هایی است که به وسیله یال‌ها به هم متصل شده‌اند. ما در این نوشته به طور خاص درخت‌های دودویی یا درخت‌های جستجوی دودویی (باینری) را بررسی می‌کنیم. درخت دودویی نوع خاصی از ساختمان داده است که برای مقاصد ذخیره‌سازی داده مورد استفاده قرار می‌گیرد. یک درخت دودویی شرایط خاصی دارد که در آن هر گره در حالت بیشینه‌ دو فرزند دارد. یک درخت دودویی مزیت‌های یک آرایه نامرتب و هم‌چنین یک لیست پیوندی را با هم دارد. جستجوی درخت دودویی به اندازه آرایه مرتب سریع است و عملیات‌های درج و حذف نیز به اندازه لیست پیوندی سریع هستند.

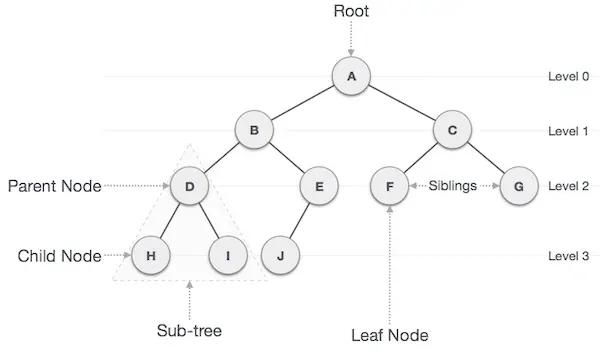
اصطلاح‌های مهم

در ادامه برخی اصطلاح‌های مهم مربوط به درخت مورد اشاره قرار گرفته است:

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

• مسیر (path) – منظور از مسیر در یک درخت، یک توالی از گره‌ها در راستای یال‌های درخت است.
• ریشه (Root) – گرهی که در بخش فوقانی درخت قرار دارد، ریشه نامیده می‌شود. هر درختی تنها یک ریشه دارد و از گره ریشه تنها یک مسیر به هر گره دیگر وجود دارد.
• والد (parent) – هر گرهی به جز گره ریشه یالی به سمت بالا به یک گره دارد، که والد آن گره نامیده می‌شود.
• فرزند (child) - گرهی که زیر یک گره مفروض قرار دارد و از طریق یالی به سمت پایین به آن وصل شده است، گره فرزند آن نامیده می‌شود.
• برگ (leaf) – گرهی که هیچ فرزندی دارد، برگ نامیده می‌شود.
• زیردرخت (Subtree) – به مجموعه فرزندان یک گره، زیردرخت گفته می‌شود.
• بازدید (Visiting) – منظور از بازدید، بررسی ارزش یک گره است، هنگامی که کنترل روی گره قرار دارد.
• پیمایش (Traversing) - منظور از پیمایش، عبور از میان گره‌های یک درخت با ترتیب خاص است.
• سطوح (Levels) – سطح یک گره نماینده نسل آن فرزند است. اگر گره ریشه در سطح 0 باشد، در این صورت فرزندان آن در سطح 1، نوه‌های آن در سطح 2 و همین طور تا آخر ... قرار دارند.
• کلیدها (Keys) – کلید نماینده ارزش یک گره بر مبنای نوع عملیات جستجویی است که قرار است روی گره انجام شود.

درخت جستجوی باینری

درخت جستجوی دودویی خصوصیات زیر را دارد:

• زیردرخت چپ یک گره کلیدی با ارزش کمتر یا مساوی کلید والد خود دارد.
• زیردرخت راست یک گره کلیدی بزرگ از کلید گره والد خود دارد.

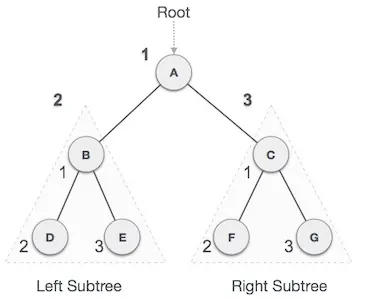
بدین ترتیب درخت جستجوی دودویی همه زیردرخت‌های خود را به دو قطعه تقسیم می‌کند: زیردرخت چپ و زیردرخت راست که به صورت زیر می‌توان تعریف کرد:

left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)

نمایش درخت جستجوی باینری

درخت جستجوی دودویی رفتار خاصی را به نمایش می‌گذارد. فرزند چپ یک گره باید ارزشی پایین‌تر از ارزش والد خود داشته باشد و فرزند سمت راست گره باید ارزشی بالاتر از ارزش والد خود داشته باشد.

درخت جستجوی دودویی مجموعه‌ای گره‌ها است که به ترتیبی چیدمان یافته‌اند که خصوصیات پیش‌گفته را حفظ می‌کنند. در هنگام جستجو کلید مطلوب در قیاس با کلیدهای درخت جستجوی دودویی بررسی می‌شود و در صورت پیدا شدن، این مقدار بازیابی می‌شود.

می‌بینیم که با توجه به گره ریشه، همه مقادیر کوچک‌تر در زیردرخت چپ قرار دارند و مقادیر بزرگ‌تر در زیردرخت راست هستند. در ادامه این درخت را با استفاده از شیء گره و اتصال آن‌ها از طریق ارجاع پیاده‌سازی می‌کنیم.

گره درخت

کدی که برای نوشتن یک گره استفاده می‌شود، شبیه کد زیر خواهد بود. این کد یک بخش داده و یک بخش ارجاع به گره‌های سمت چپ و راست خود دارد:

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

در یک درخت همه گره‌ها ساختار مشترکی (مشابهی) دارند.

عملیات‌های پایه‌ای درخت جستجوی دودویی (BST)

عملیات‌های پایه‌ای که می‌توان بر روی یک ساختمان داده درخت جستجوی دودویی اجرا کرد به صورت زیر هستند:
درج (Insert) – یک عنصر را در یک درخت درج می‌کند/ یک درخت ایجاد می‌کند.

• جستجو (Search) - به دنبال یک عنصر در درخت می‌گردد.
• پیمایش پیش‌ترتیبی (Preorder Traversal) - یک درخت را به روش پیش‌ترتیبی پیمایش می‌کند
• پیمایش میان‌ترتیبی (Inorder Traversal) - یک درخت را به روش میان‌ترتیبی پیمایش می‌کند.
• پیمایش پس‌ترتیبی (Postorder Traversal) - یک درخت را به روش پس‌ترتیبی پیمایش می‌کند.

در ادامه ایجاد (درج درون) یک ساختمان داده درخت و شیوه جستجوی یک آیتم داده‌ای را در یک درخت می‌آموزیم. همچنین در مورد روش‌های پیمایش در بخش بعدی، مواردی را بررسی خواهیم کرد.

عملیات درج

نخستین عملیات درج به ایجاد درخت اختصاص دارد. پس از آن هر زمان که بخواهید یک عنصر در درخت درج کنید، ابتدا موقعیت مناسب را می‌یابید. جستجو از گره ریشه آغاز می‌شود، سپس اگر ارزش داده کمتر از ارزش کلید باشد، به دنبال موقعیت خالی در زیردرخت سمت چپ می‌گردیم و داده را در آن درج می‌کنیم. در غیر این صورت به دنبال یک موقعیت خالی در زیردرخت راست می‌گردیم و داده‌ها را درج می‌کنیم.

الگوریتم

If root is NULL 
   then create root node
return

If root exists then
   compare the data with node.data
   
   while until insertion position is located

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree

   endwhile 
   
   insert data
	
end If      

پیاده‌سازی

پیاده‌سازی تابع درج می‌تواند مانند کد زیر باشد:

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
			
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

عملیات جستجو

هر زمان که یک عنصر قرار است در درخت مورد جستجو قرار گیرد، عملیات جستجو از گره ریشه آغاز می‌شود، سپس اگر داده کمتر از ارزش کلید باشد، به دنبال موقعیت عنصر در زیردرخت سمت چپ می‌گردیم. در غیر این صورت موقعیت عنصر در زیردرخت راست بررسی می‌شود. از همین الگوریتم برای هر گره جدید استفاده می‌شود.

الگوریتم

If root.data is equal to search.data
   return root
else
   while data not found

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree
         
      If data found
         return node
   endwhile 
   
   return data not found
   
end if  

پیاده‌سازی

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }

      return current;
   }  
}

پیاده‌سازی کامل الگوریتم پیمایش درخت در زبان C

پیمایش درخت فرایندی است که در طی آن همه گره‌های یک درخت مورد بازدید قرار می‌گیرند و احتمالاً مقادیر آن‌ها نیز پرینت می‌شود. از آنجا که همه گره‌ها از طریق یال (لینک) ها به هم مربوط هستند، ما همواره از گره ریشه (رأس) درخت آغاز می‌کنیم. بدین ترتیب نمی‌توان به یک گره درخت به صورت تصادفی دسترسی یافت. سه روش برای پیمایش یک درخت وجود دارد:

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

• پیمایش پیش‌ترتیبی
• پیمایش میان‌ترتیبی
• پیمایش پس‌ترتیبی

به طور کلی منظور ما از پیمایش یک درخت، جستجوی یک مقدار یا کلید خاص در درخت و یا نمایش همه مقادیر درون آن است.

پیمایش میان‌ترتیبی

در این روش از پیمایش، زیردرخت چپ ابتدا بازدید می‌شود، سپس از گره ریشه بازدید می‌شود و در نهایت زیردرخت راست پیمایش می‌شود. همواره باید به خاطر داشته باشید که هر گره می‌تواند خود نماینده یک زیردرخت باشد.

اگر یک درخت باینری به صوت میان‌ترتیبی پیموده شود، مقادیر کلیدهای ذخیره شده در خروجی به ترتیب صعودی نمایش داده می‌شود.

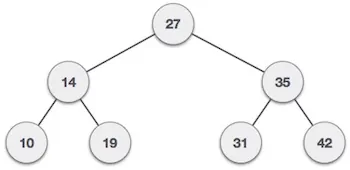
از گره A آغاز می‌کنیم و با پیمایش میان‌ترتیبی ادامه می‌دهیم. به گره زیردرخت چپ یعنی B می‌رویم. B نیز به صورت میان‌ترتیبی پیمایش می‌شود. این فرایند تا زمانی که همه گره‌ها بازدید شوند ادامه می‌یابد. خروجی پیمایش میان‌ترتیبی درخت فوق به صورت زیر خواهد بود:

D → B → E → A → F → C → G

الگوریتم

• تا زمانی که همه گره‌ها بازدید شوند:
• گام 1- زیردرخت چپ را به صورت بازگشتی پیمایش کن
• گام 2 – گره ریشه را بازدید کن
• گام 3 – زیردرخت سمت راست را به صورت بازگشتی پیمایش کن.

پیمایش پیش‌ترتیبی

در این روش پیمایش، گره ریشه ابتدا مورد بازدید قرار می‌گیرد، سپس زیردرخت چپ و در نهایت زیردرخت راست پیموده می‌شوند.

کار خود را از گره A آغاز می‌کنیم و سپس به صورت پیش‌ترتیبی ادامه می‌دهیم. ابتدا خود گره A و سپس به زیردرخت چپ (B) می‌رویم. B نیز به صورت پیش‌ترتیبی مورد پیمایش قرار می‌گیرد. این فرایند تا زمانی که همه گره‌ها مورد بازدید قرار گیرند ادامه می‌یابد. خروجی پیمایش پیش‌ترتیبی درخت فوق به صورت زیر خواهد بود:

A → B → D → E → C → F → G

الگوریتم

• تا زمانی که همه گره‌ها پیمایش شوند:
• گام 1 – از گره ریشه بازدید کن.
• گام 2 – زیردرخت چپ را به صورت بازگشتی پیمایش کن.
• گام 3 – زیردرخت راست را به صورت بازگشتی پیمایش کن.

پیمایش پس‌ترتیبی

در این روش پیمایش، جنان که از روی نام مشخص است گره ریشه در آخر بازدید می‌شود. بنابراین ابتدا زیردرخت سمت چپ و بعد از آن زیردرخت راست و در نهایت گره ریشه بازدید می‌شوند.

کار خود را از گره A آغاز می‌کنیم و از روش پیمایش پس‌ترتیبی استفاده می‌کنیم. ابتدا زیردرخت چپ (گره B) می‌رویم. B به صورت پس‌ترتیبی پیمایش می‌شود. این فرایند تا زمانی که همه گره‌ها بازدید شوند ادامه می‌یابد. خروجی پیمایش پس‌ترتیبی به صورت زیر خواهد بود:

D → E → B → F → G → C → A

الگوریتم:

• تا زمانی که همه گره‌ها پیمایش شوند:
• گام 1 – زیردرخت چپ را به صورت بازگشتی پیمایش کن.
• گام 2 - زیردرخت راست را به صورت بازگشتی پیمایش کن.
• گام 3 – از گره ریشه بازدید کن.

با فرض وجود درخت باینری زیر، در ادامه الگوریتم پیمایش این درخت را به طور کامل در زبان C پیاده‌سازی کرده‌ایم:

پیاده‌سازی در C

#include 
#include 

struct node {
   int data; 
	
   struct node *leftChild;
   struct node *rightChild;
};

struct node *root = NULL;

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;

      while(1) { 
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }  //go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
         printf("%d ",current->data); 

      //go to left tree
      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }
   }
   
   return current;
}

void pre_order_traversal(struct node* root) {
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}

void inorder_traversal(struct node* root) {
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);          
      inorder_traversal(root->rightChild);
   }
}

void post_order_traversal(struct node* root) {
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}

int main() {
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };

   for(i = 0; i < 7; i++) insert(array[i]); i = 31; struct node * temp = search(i); if(temp != NULL) { printf("[%d] Element found.", temp->data);
      printf("\n");
   }else {
      printf("[ x ] Element not found (%d).\n", i);
   }

   i = 15;
   temp = search(i);

   if(temp != NULL) {
      printf("[%d] Element found.", temp->data);
      printf("\n");
   }else {
      printf("[ x ] Element not found (%d).\n", i);
   }            

   printf("\nPreorder traversal: ");
   pre_order_traversal(root);

   printf("\nInorder traversal: ");
   inorder_traversal(root);

   printf("\nPost order traversal: ");
   post_order_traversal(root);       

   return 0;
}

اگر کد فوق را کامپایل کرده و اجرا کنیم، نتیجه زیر به دست می‌آید:

خروجی

Visiting elements: 27 35 [31] Element found.
Visiting elements: 27 14 19 [ x ] Element not found (15).

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

اگر این نوشته مورد توجه شما قرار گرفته است، احتمالاً موارد زیر نیز برای شما جذاب خواهند بود:

• آموزش درخت در نظریه گراف و کاربردها
• همه چیز در مورد درخت تصمیم (Decision Tree)
• مجموعه آموزش‌های مهندسی نرم افزار
• دانلود رایگان کتاب آموزش ساختمان داده ها
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R): درخت تصمیم
• ۳۰ پرسش و پاسخ درباره‌ی مدل‌های درختی
• مجموعه آموزش‌های علوم کامپیوتر

==