ساختمان هیپ در درخت های دودویی — به زبان ساده

در سال 1964، جی. ویلیامز (J. Williams) یک کانادایی که اصالتاً اهل ولز بود، ساختاری برای یافتن مقدار بیشینه طراحی کرد. این ساختار «هیپ» (heap) نام گرفت. هیپ یک درخت نیمه مرتب است که در آن مقدار بیشینه (یا کمینه) در رأس درخت قرار میگیرد.
چرا باید از هیپ استفاده کنیم؟
تصور کنید شما مسئول یک بیمارستان هستید و چندین بیمار در اتاق انتظار قرار دارند. از آنجا که هر بیماری منتظر پزشک است، بیماران یک صف را تشکیل دادهاند. اینک فرض کنید یک بیمار جدید با وضعیتی اورژانسی به داخل بیمارستان منتقل میشود. آیا این بیمار باید در انتهای صف قرار گیرد یا باید به این بیمار اولویت جداگانهای بدهیم؟
مفهوم اولویت دادن مانند مثال فوق در بیمارستان ارتباط نزدیکی با طرز کار ساختار هیپ دارد. هیپ نیز مقادیر دارای اولویت بالاتر را در درخت اولویت میدهد و مقادیر کوچکتر به انتهای درخت میروند.
ماهیت هیپ چیست؟
هیپ یک درخت دودویی است که دو مشخصه اضافی به صورت زیر دارد:
- هیپ کامل است. این بدان معنی است که هر شاخه درخت (به جز احتمالاً سطح آخر) هر دو گره را دارد.
- هیپ نیمه مرتب است. این بدان معنی است که مقدار در سطوح بالاتر همواره مقدار بیشتر از سطوح پایینتر دارد و به این ترتیب گره رأس همواره مقدار بیشینه است.
برای توضیح بیشتر به تصویر زیر نگاه کنید:
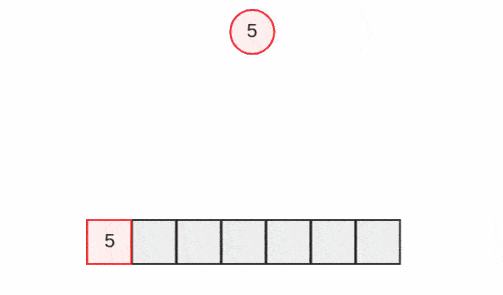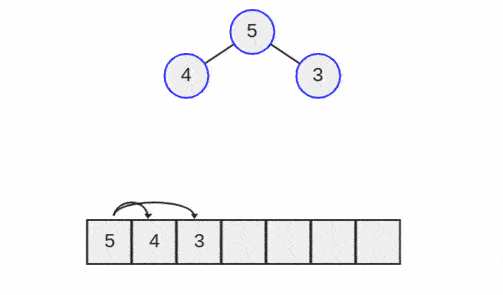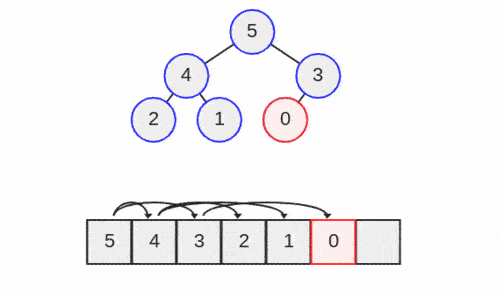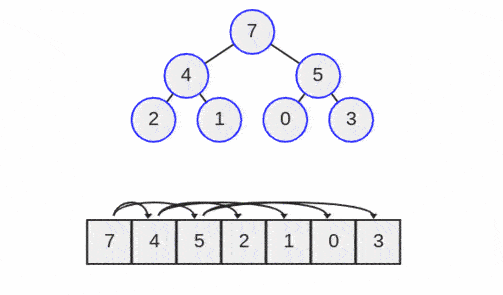
دقت کنید که هفت بزرگتر از پنج و چهار است و پنج و چهار نیز بزرگتر از صفر، یک، دو و سه هستند. هیپها به دلیل کامل بودن، معمولاً درون یک بلوک پیوسته از حافظه مانند یک آرایه پیادهسازی میشوند.
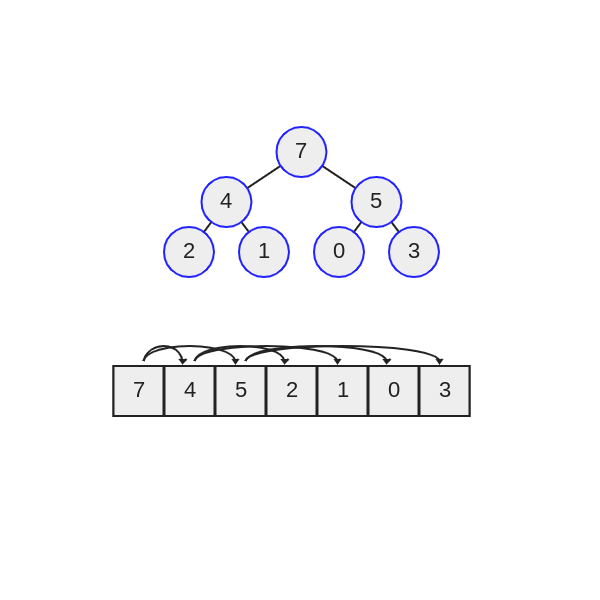
اینک به اتصال درخت باینری آرای خاص زیر توجه کنید:
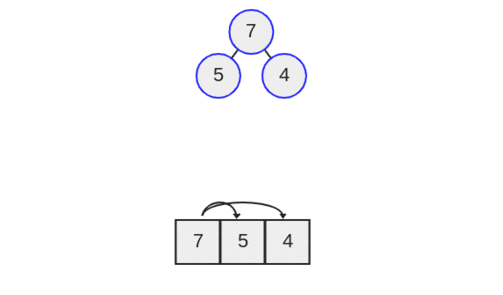
در تصویر فوق، گره رأس درخت مقدار 7 را دارد که نخستین اندیس آرایه است و به صورت arr[0] = 7 توصیف میشود.
اینک به پیکانهای روی آرایه توجه کنید که اتصالهای درخت دودویی را نشان میدهند. پیکان سمت چپ از رأس درخت به عدد 5 اشاره میکند که در آرایه به صورت arr[1] = 5 مشاهده میشود و پیکان سمت راست به عدد چهار اشاره میکند که در آرایه به صورت arr[2] = 4 است.
این اتصال از والد به فرزند میتواند در هر گرهی در آرایه با ضرب کردن اندیس i*2+1 (چپ) و i*2+2 (راست) به دست آید.
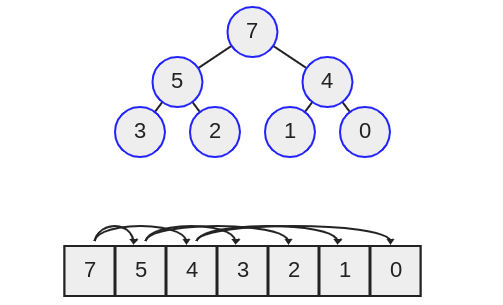
بنابراین اکنون به گرهی که دارای مقدار چهار است نگاه میکنیم، فرزندان میتوانند در درخت دودویی با ردگیری شاخهها به دست آیند که ما را به مقادیر یک یا صفر منتهی میکند. همچنین میتوانیم با نگاه کردن به آرایه ببینیم که arr[2] = 4 است و از این رو فرزند چپ به صورت arr[i*2+1] = arr[2*2+1] = arr[5] = 1 و فرزند راست به صورت arr[6] = 2 است.
در ادامه به روش نگهداری هیپ میپردازیم. عمل up heap زمانی رخ میدهد که یک گره در هیپ درج میشود و مشخصه ترتیب هیپ به هم میریزد. گرهها همواره به سمت چپترین گرههای موجود اضافه میشوند (چون هیپ یک درخت کامل است)؛ اما هیپها نیمه مرتب نیز هستند و از این رو باید عمل up heap روی آنها صورت بگیرد.
این وضعیت را با مثالی توضیح میدهیم. در هیپ زیر به مقدار تازه اضافه شده 7 توجه کنید.
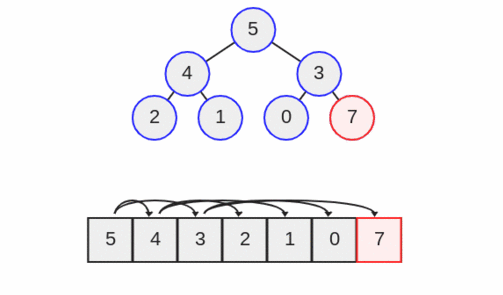
گره جدید در اندیس موجود بعدی آرایه (یعنی سمت چپترین برگ ممکن) قرار میگیرد؛ اما عدد هفت بزرگتر از آن است که در این سطح وارد شود و از این رو مشخصه نیمه مرتب هیپ از دست میرود. بدین ترتیب به یک عمل up heap نیاز داریم. جای هفت را به سه عوض میکنیم.
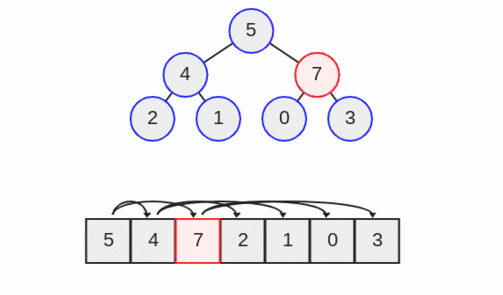
اینک در سطح بالاتر عمل up heap مجدداً بررسی میشود. آیا هفت از عدد موجود در سطح بعدی بزرگتر است؟ بله چنین است و از این رو مجدداً عمل up heap را تکرار میکنیم.
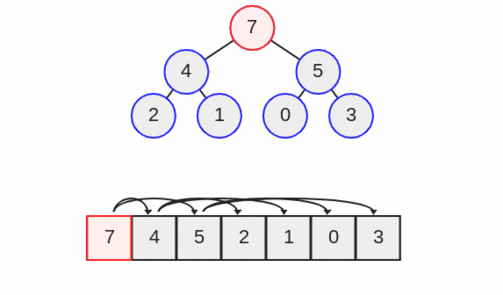
اینک هفت را با پنج تعویض میکنیم و به سطح بالاتر میرویم. میبینید که هفت از این بالاتر نمیتواند برود. بدین ترتیب هفت که به عنوان یک برگ به درخت هیپ اضافه شده بود، با استفاده از عمل up heap در درخت به سمت بالا حرکت کرد و به رأس درخت رسید.
این حالت صحیح است، زیرا اینک اگر به هیپ نگاه کنید متوجه میشوید که هفت در واقع بزرگترین مقدار در هیپ است. به همین دلیل در این مثال، هفت بالاترین اولویت را در درخت دارد.
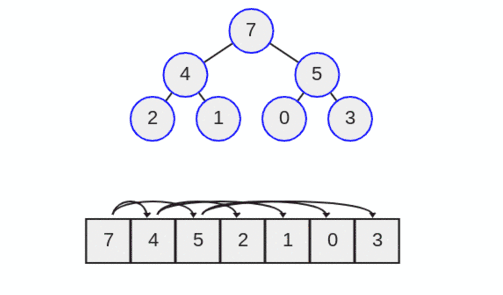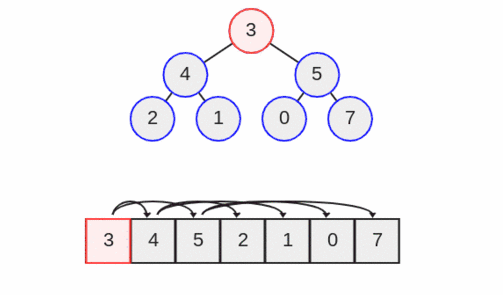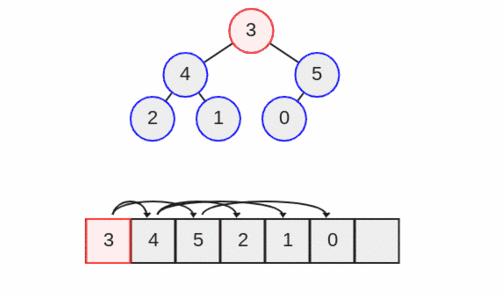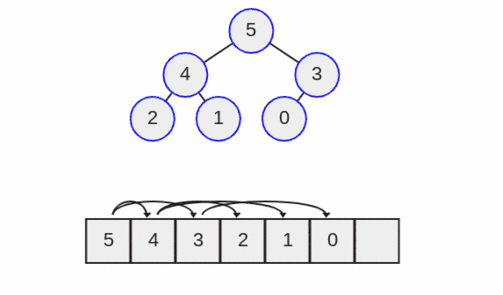
در ادامه عمل down heap را نیز معرفی میکنیم. در هیپها میتوان تنها گره رأس یعنی مقدار بیشینه را حذف کرد. یک عمل down heap را از مقدار بیشینه آغاز میکنیم و این مقدار بیشینه را با سمت چپترین برگ هیپ تعویض میکنیم. بدین ترتیب همان طور که در تصویر زیر میبینید عدد هفت با عدد 3 تعویض میشود.
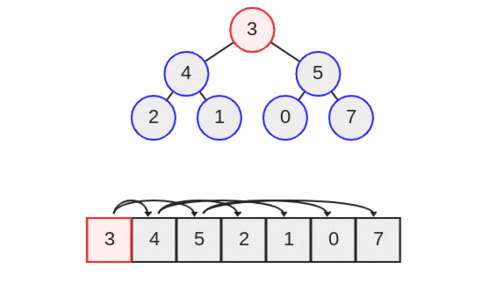
سپس گره آخر را حذف میکنیم. بدین ترتیب هفت از هیپ حذف میشود.
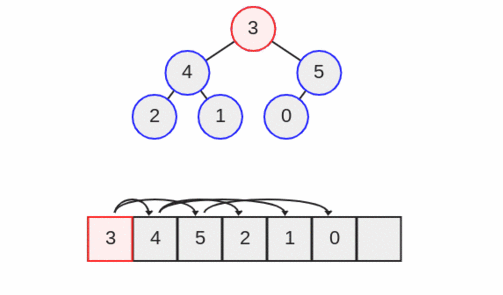
اینک از عمل down heap استفاده میکنیم تا مشخصه نیمه مرتب بودن هیپ را حفظ کنیم. به این منظور باید گره رأس را با دو گره زیر خود مقایسه کنیم.
اگر گره یا گرههای سطح پایینتر، بزرگتر باشند، با گره رأس تعویض میشوند. اعداد چهار و پنج هر دو از سه بزرگ هستند. از این رو پنج که گره بزرگتر در سطح پایینتر است با سه تعویض میشود.
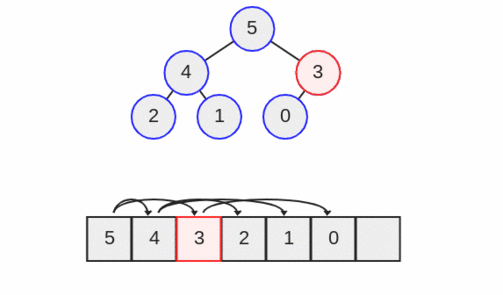
عمل down heap تا زمانی که گره به برگ برسد و یا مشخصه نیمه مرتب حفظ شود تداوم مییابد.
در این مثال، سه بزرگتر از گره (های) برگ سطح پایینتر یعنی 0 میشود و از این رو عمل down heap پایان یافته است.
چگونه از هیپ استفاده کنیم؟
این بخش را به صورت ساده و با ارائه تعریف کلاس هیپ آغاز میکنیم.
1class Heap {
2
3private:
4 int* tree;
5 int max_size, size;
6
7 //more code//دقت کنید که یک int* tree، یک max_size و یک size در تعریف کلاس هیپ وجود دارند. عبارت int* tree آرایه است، که بزرگی آن به اندازه max_size خواهد بود. size نیز اندازه کنونی هیپ را برای کد ما مشخص میکند که هنگام افزودن یا حذف کردن گرهها حائز اهمیت خواهد بود. در ادامه برخی تابعهای کمکی را با نامهای swap، parent، left و right تعریف میکنیم:
1void swap(const int& i, const int& j) {
2 const int temp_val = tree[i];
3 tree[i] = tree[j];
4 tree[j] = temp_val;
5 }
6
7const int parent(const int& child) {
8 return ( (child - 1)/2 );
9 }
10
11const int left_child(const int& parent) {
12 return ( parent*2 + 1 );
13 }
14
15 const int right_child(const int& parent) {
16 return ( parent*2 + 2 );
17 }همان طور که در بخش قبلی تعریف کردیم، فرزندان به ترتیب به صورت i*2 + 1 و i*2 + 2 هستند و والد در گره floor((i-1)/2) قرار دارد. تابع swap به تعویض مکان گرهها میپردازد.
سپس تابعی مینویسیم که اندازه درخت را افزایش میدهد. به بیان دیگر در این تابع کارهایی که هنگام برقرار بودن شرط size ≥ max_size باید انجام دهیم تعریف شده است:
1void grow_tree() {
2 max_size = max_size << 1 | 1;
3 int* prev_tree = tree;
4 tree = new int[max_size];
5 for(int i=0; i<size; i++)
6 tree[i] = prev_tree[i];
7 delete[] prev_tree;
8 }یک درخت کامل و پر حداکثر 2^n-1 گره میتواند داشته باشد. از این رو max_size همواره باید برابر با 2^n-1 باشد. خط کدی که این کار را انجام میدهد به صورت زیر است:
1max_size = max_size << 1 | 1;کد بیتی این کار را میتوان چنین ترجمه کرد: «بیتها را به سمت چپ شیفت بده و سپس یک واحد اضافه کن».
تابع زیر به منظور درج مقداری در هیپ استفاده میشود.
1void insert(const int val) {
2 if( size == max_size )
3 grow_tree();
4 tree[size] = val;
5 upHeap(size++);
6}تابع insert با بررسی گرهی که باید رشد کند آغاز میشود و اگر شرایط وجود داشت این کار انجام میگیرد. سپس گره جدید به عنوان آخرین مدخل در درخت درج میشود و در ادامه عمل up heap صورت میپذیرد. دقت کنید که اندازه (size) هیپ با عملگر افزایشی (post-increment) به صورت ++size افزایش مییابد.
1void upHeap(const int child) {
2 const int root = 0
3 if( child == root)
4 return;
5 if( tree[child] > tree[parent(child)] ) {
6 swap( child, parent(child) );
7 upHeap( parent(child) );
8 }
9}عمل up heap یک تابع بازگشتی است. همه تابعهای بازگشتی یک حالت مبنا دارند. در مورد up heap، حالت مبنا داشتن یک گره در رأس (ریشه) برای تعویض شدن است. از سوی دیگر اگر گره ورودی در رأس نباشد، بررسی میشود که آیا باید یک تعویض صورت بگیرد یا نه و اگر چنین باشد تعویض میشود و این کار در سطوح بالاتر نیز تکرار میشود.
اینک به توضیح روش حذف از هیپ میپردازیم.
1void remove() {
2 const int root = 0;
3 if( size == 0 )
4 return;
5 swap(root, --size);
6 downHeap(root);
7}همان طور که در بخش قبلی توضیح دادیم، کار خود را با تعویض گره رأس با گره آخر هیپ شروع میکنیم و سپس از سمت رأس به سمت پایین هیپ حرکت میکنیم.
دقت کنید که عملگر کاهشی size-- برای کاهش اندازه هیپ استفاده میشود:
1void downHeap(const int parent) {
2 if( right_child(parent) >= size )
3 return;
4
5 int temp = parent;
6 if( tree[temp] < tree[left_child(parent)] )
7 temp = left_child(parent);
8
9 if( tree[temp] < tree[right_child(parent)] )
10 temp = right_child(parent);
11
12 if( temp != parent ) {
13 swap( parent, temp );
14 downHeap(temp);
15 }
16
17}Down heap نیز یک تابع بازگشتی است. این بار حالت مبنا زمانی است که عمل Down heap به گره برگ میرسد یعنی دیگر امکان پایینتر رفتن وجود ندارد. در غیر این صورت، عمل Down heap بررسی کرده و گرههای بزرگتر را در سطوح پایینتر پیدا میکند و عمل تعویض را انجام داده و سپس این فرایند را در سطوح پایینتر نیز تکرار میکند.
اینک میتوانیم کد مطرح شده در این مقاله را جمعبندی کنیم و ساختمان داده هیپ را ایجاد کنیم. کد کامل ساختمان داده هیپ در زبان ++C به صورت زیر است:
1#include <iostream>
2
3using namespace std;
4
5class Heap {
6
7 private:
8 int* tree;
9 int max_size, size;
10
11 void grow_tree() {
12 max_size = max_size << 1 | 1;
13 int* prev_tree = tree;
14 tree = new int[max_size];
15 for(int i=0; i<size; i++)
16 tree[i] = prev_tree[i];
17 delete[] prev_tree;
18 }
19
20 void swap(const int& i, const int& j) {
21 const int temp_val = tree[i];
22 tree[i] = tree[j];
23 tree[j] = temp_val;
24 }
25
26 const int parent(const int& child) {
27 return ( (child - 1)/2 );
28 }
29
30 const int left_child(const int& parent) {
31 return ( parent*2 + 1 );
32 }
33
34 const int right_child(const int& parent) {
35 return ( parent*2 + 2 );
36 }
37
38 void upHeap(const int child) {
39 const int root = 0;
40 if( child == root )
41 return;
42 else if( tree[child] > tree[parent(child)] ) {
43 swap( child, parent(child) );
44 upHeap( parent(child) );
45 }
46 }
47
48 void downHeap(const int parent) {
49 if( right_child(parent) >= size )
50 return;
51 int temp = parent;
52
53 if( tree[temp] < tree[left_child(parent)] )
54 temp = left_child(parent);
55
56 if( tree[temp] < tree[right_child(parent)] )
57 temp = right_child(parent);
58
59 if( temp != parent ) {
60 swap( parent, temp );
61 downHeap(temp);
62 }
63
64 }
65
66 public:
67 Heap() : max_size(1), size(0), tree(new int[1]) {};
68
69 void print() {
70 cout<<"Heap:[ ";
71 for(int i=0; i<size; i++)
72 cout<<tree[i]<<" ";
73 cout<<"]\n";
74 }
75
76 void insert(const int val) {
77 if( size == max_size )
78 grow_tree();
79 tree[size] = val;
80 upHeap(size++);
81 }
82
83 void remove() {
84 const int root = 0;
85 if( size == root )
86 return;
87 swap(root, --size);
88 downHeap(root);
89 }
90};
91
92int main() {
93 Heap h;
94 cout<<"Adding nodes to heap.\n";
95 h.insert(5);
96 h.print();
97 h.insert(4);
98 h.print();
99 h.insert(3);
100 h.print();
101 h.insert(2);
102 h.print();
103 h.insert(1);
104 h.print();
105 h.insert(0);
106 h.print();
107 h.insert(7);
108 h.print();
109 cout<<"\nRemoving node(s) from heap.\n";
110 h.remove();
111 h.print();
112
113 return 0;
114}این کد را در یک فایل به نام main.cpp کپی کنید و آن را با استفاده از دستور زیر از خط فرمان کامپایل کنید:
g++ main.cpp -o Heap.exe
سپس کد زیر را از خط فرمان اجرا کنید:
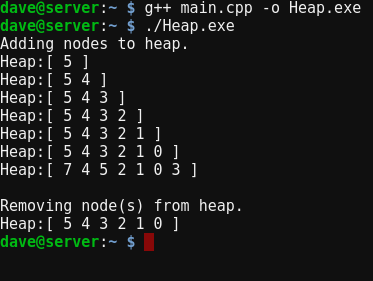
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش ساختمان داده ها
- مجموعه آموزشهای مهندسی نرم افزار
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
- آموزش پیشرفته ساختمان داده (همراه با حل نمونه سوالات کنکور ارشد و دکتری)
- آموزش درهم سازی در ساختمان داده
- درخت هیپ (Heap) و کاربردهای آن — به زبان ساده
==












