گراف — ساختار داده و الگوریتم ها

۶۸۳۴ بازدید

آخرین به‌روزرسانی: ۸ خرداد ۱۴۰۳

زمان مطالعه: ۸ دقیقه

دانلود PDF مقاله

گراف نوعی بازنمایی تصویری از مجموعه‌ای اشیا است که در آن برخی جفت‌ها از طریق پیوندهایی با هم ارتباط دارند. اشیای به هم متصل به وسیله نقاطی که رأس نام دارند و پیوندهای اتصالی بین آن‌ها یال نامیده می‌شوند.

فهرست مطالب این نوشته

عملیات‌های پایه

پیمایش گراف

پیمایش سطح-اول

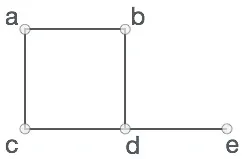
به طور رسمی گراف جفتی از مجموعه (V, E) است که در آن V مجموعه از رئوس و E مجموعه‌ای از یال‌ها است که رئوس را به هم متصل می‌سازند. نگاهی به گراف زیر بیندازید:

در گراف فوق:

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

گراف‌های ریاضی را می‌توان به وسیله ساختارهای داده بازنمایی کرد. ما می‌توانیم گراف را با استفاده از آرایه‌ای از رئوس و یک آرایه دو بعدی از یال‌ها نشان دهیم. پیش از آن که به ادامه مطلب بپردازیم، ابتدا با برخی اصطلاح‌های مهم این حوزه آشنا می‌شویم:

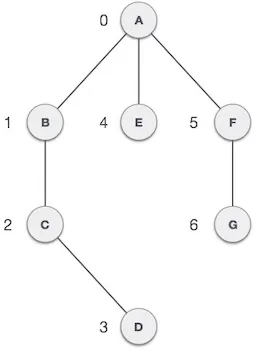
رأس – هر گره در گراف به شکل یک رأس نمایش می‌یابد. در شکل زیر دایره‌هایی که نوشته دارند رئوس هستند بدین ترتیب نقاطی که با حروف A تا G مشخص شده‌اند، رأس‌های گراف محسوب می‌شوند. آن‌ها را می‌توانیم با استفاده از یک آرایه که در تصویر زیر نمایش یافته است نشان دهیم. در این آرایه A در اندیس 0 قرار دارد، B در اندیس 1 است و همین طور تا آخر.
یال – به مسیر بین دو رأس یا خطی که بین رئوس برقرار می‌شود، یال می‌گوییم. در مثال زیر، خط از A تا B، از B تا C و همین طور تا آخر یال‌های گراف محسوب می‌شوند. می‌توان از آرایه‌ای دو بعدی مانند آنچه در تصویر زیر قرار دارد، برای نمایش یال‌های گراف استفاده کرد. در این آرایه AB به معنی یال بین رأس‌های A و B است که در ردیف 0، ستون 1 قرار دارد، یال BC در ردیف 1، ستون 2 و همین طور تا آخر همه یال‌ها مشخص شده‌اند. ترکیب‌هایی که یالی ندارند مقدار صفر دارند.
مجاورت – دو گره یا رأس در صورتی مجاور خوانده می‌شوند که از طریق یالی به هم وصل شده باشند. در مثال زیر رأس B با رئوس A و رأس C با B مجاور است.
مسیر – به یک توالی از یال‌ها بین دو رأس، مسیر گفته می‌شود. در مثال زیر ABCD نشان دهنده وجود مسیری از رأس A تا D است.

عملیات‌های پایه

در ادامه برخی از عملیات‌های مقدماتی گراف شرح داده شده‌اند:

فیلم آموزش گراف در ساختمان گسسته (رایگان) در فرادرس

کلیک کنید

افزودن رأس (Add Vertex): این عملیات یک رأس به گراف اضافه می‌کند.
افزودن یال (Add Edge): این عملیات بین دو رأس موجود در گراف یالی برقرار می‌سازد.
نمایش رأس (Display Vertex): یک رأس را در گراف نمایش می‌دهد.

پیمایش گراف

به حرکت بین رئوس مختلف از طریق یال‌ها، پیمایش گراف گفته می‌شود. پیمایش کلی یک گراف شامل همه رئوس آن است. در مواردی نیز ممکن است تنها به پیمایش جزء خاصی از یک گراف بین رئوس معین نیاز داشته باشیم. در هر حال برای پیمایش یک گراف روش‌های مختلفی وجود دارد که در ادامه بیشتر بررسی می‌کنیم.

پیمایش عمق-اول (Depth First)

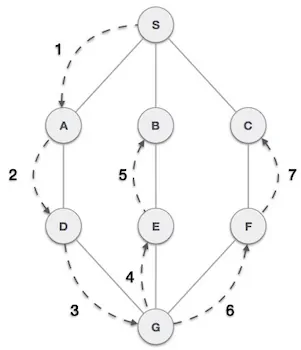
الگوریتم جستجوی عمق –اول طوری یک گراف را پیمایش می‌کند که اولویت آن با پیمایش عمقی گراف است و از یک پشته برای به‌خاطرسپاری رأس‌های بعدی جهت جستجو استفاده می‌کند و زمانی که وارد یک بن‌بست شود، از تکرار بهره می‌گیرد.

الگوریتم پیمایش عمق-اول همان طور که در شکل فوق مشخص است، ابتدا از S به A به D به G به E به B می‌رود، سپس به F و در نهایت به C می‌رود. قواعد این پیمایش چنین است:

قاعده 1: به رأس بازدید نشده مجاور برو. آن را به صورت بازدید شده علامت‌گذاری کن. آن را وارد پشته بکن.
قاعده 2: اگر رأس مجاوری نمانده باشد، یک رأس را از پشته pop کنید. (همه رئوسی که رأس‌های مجاور ندارند، از پشته pop می‌شوند).
قاعده 3: قاعده 1 و قاعده 2 را تا زمانی که پشته خالی شود، ادامه بده.

گام	پیمایش	توضیح
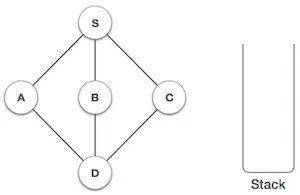
1		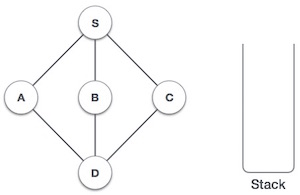مقدار دهی اولیه پشته.
2		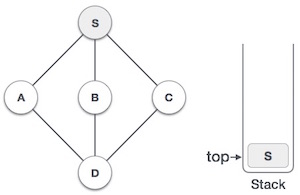رأس S به عنوان رأس بازدید شده نشانه‌گذاری می‌شود و در پشته قرار می‌گیرد. هر گونه گره‌های بازدید نشده مجاور گره S بررسی می‌شوند. سه گره داریم که می‌توانیم هر یک از آن‌ها را انتخاب کنیم. در این مثال، این گره را با ترتیب الفبایی انتخاب می‌کنیم.
3		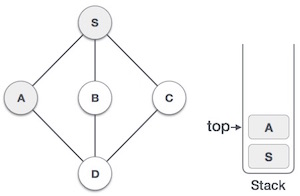رأس A را به عنوان بازدید شده نشانه‌گذاری می‌کنیم و آن را در پشته قرار می‌دهیم. همه گره‌های مجاور بازدید نشده را بررسی می‌کنیم. هر دو گره S و D مجاور A هستند؛ اما ما تنها به دنبال گره‌های بازدید نشده هستیم.
4		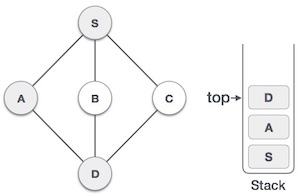رأس D را به عنوان بازدید شده نشانه‌گذاری می‌کنیم و آن را درون پشته قرار می‌دهیم. در این جا رأس B و C را داریم که مجاور D هستند و هر دو بازدید نشده هستند. با این حال باز هم می‌توانیم با ترتیب الفبایی انتخاب کنیم.
5		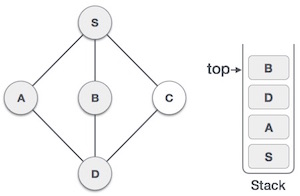رأس B را انتخاب می‌کنیم و آن را به عنوان بازدید شده نشانه‌گذاری کرده و در پشته قرار می‌دهیم. در این مرحله B هیچ رأس مجاوری ندارد. بنابراین رأس B را از پشته بر می‌داریم (pop).
6		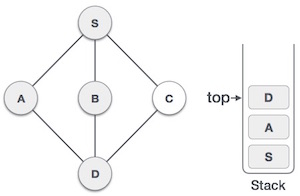آیتم top پشته را برای یافتن گره قبلی بررسی می‌کنیم و تست می‌کنیم که آیا گره‌های بازدید نشده دارد یا نه. در این مرحله، D را در بخش top پشته می‌یابیم.
7		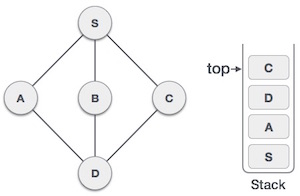تنها گره مجاور بازدید نشده رأس‌های D و C هستند. بنابراین از رأس C بازدید می‌کنیم و آن را به عنوان بازدید شده در پشته قرار می‌دهیم.

از آنجا که C هیچ گره مجاور بازدید نشده‌ای دارد، بنابراین مقادیر فوقانی پشته را بر می‌داریم تا جایی که گرهی را بیابیم که گره مجاور بازدید نشده داشته باشد. در این مثال چنین گرهی وجود ندارد و بنابراین تا زمانی که پشته خالی شود به pop کردن آن ادامه می‌دهیم.

پیاده‌سازی الگوریتم جستجوی عمق-اول در زبان C

مثالی که در بخش فوق را بررسی کردیم را در زبان C مدل‌سازی کرده‌ایم.

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 5

struct Vertex {
   char label;
   bool visited;
};

//stack variables

int stack[MAX]; 
int top = -1; 

//graph variables

//array of vertices
struct Vertex* lstVertices[MAX];

//adjacency matrix
int adjMatrix[MAX][MAX];

//vertex count
int vertexCount = 0;

//stack functions

void push(int item) { 
   stack[++top] = item; 
} 

int pop() { 
   return stack[top--]; 
} 

int peek() {
   return stack[top];
}

bool isStackEmpty() {
   return top == -1;
}

//graph functions

//add vertex to the vertex list
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

//add edge to edge array
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//display the vertex
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       

//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;

   for(i = 0; i < vertexCount; i++) {
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) {
         return i;
      }
   }

   return -1;
}

void depthFirstSearch() {
   int i;

   //mark first node as visited
   lstVertices[0]->visited = true;

   //display the vertex
   displayVertex(0);   

   //push vertex index in stack
   push(0);

   while(!isStackEmpty()) {
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());

      //no adjacent vertex found
      if(unvisitedVertex == -1) {
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }

   //stack is empty, search is complete, reset the visited flag        
   for(i = 0;i < vertexCount;i++) {
      lstVertices[i]->visited = false;
   }        
}

int main() {
   int i, j;

   for(i = 0; i < MAX; i++)    // set adjacency {
      for(j = 0; j < MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;
   }

   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4

   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D

   printf("Depth First Search: ")
   depthFirstSearch(); 

   return 0;   
}

اگر کد فوق را کامپایل و اجرا کنیم، نتیجه زیر به دست می‌آید.

خروجی

Depth First Search: S A D B C

پیمایش سطح-اول

الگوریتم جستجوی سطح-اول، گراف را با حرکت در سطح پیمایش می‌کند و از صف برای به‌خاطرسپاری رأس‌های بعدی که می‌خواهد جستجو کند استفاده می‌کند و هر زمان که وارد بن‌بست شود از چرخه استفاده می‌کند.

در مثال فوق الگوریتم سطح-اول ابتدا از رأس A به B به E و به F می‌رود و. سپس به C و در نهایت از G به D می‌رود. قواعد این پیمایش چنین هستند:

قاعده اول: از رأس بازدید نشده مجاور بازدید کن. آن را به صورت بازدید شده نشانه‌گذاری کن، آن را نمایش بده و در صف درج کن.
قاعده 2: اگر هیچ رأس مجاوری وجود ندارد، نخستین رأس را از صف خارج کن.
قاعده 3: قواعد 1 و 2 را تا زمانی که صف خالی شود ادامه بده.

گام	پیمایش	توضیح
1		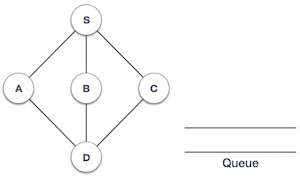مقداردهی اولیه صف
2		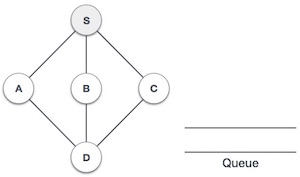کار خود را از رأس S (گره آغازین) شروع می‌کنیم و آن را بازدید شده نشانه‌گذاری می‌کنیم.
3		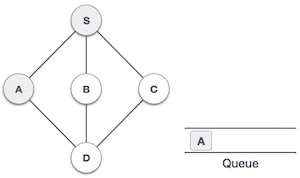سپس می‌بینیم که در S یک گره مجاور بازدید نشده وجود دارد. در این مثال، سه گره داریم؛ اما به صورت الفبایی رأس A را انتخاب می‌کنیم، آن را به صورت بازدید شده نشانه‌گذاری کرده وارد صف می‌کنیم.
4		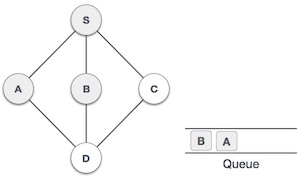سپس می‌بینیم که گره مجاور بازدید نشده از S، گره B است. آن را به عنوان بازدید شده نشانه گذرای کرده و در صف قرار می‌دهیم.
5		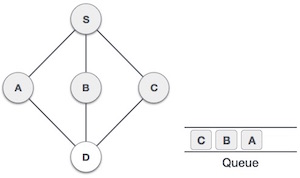سپس گره مجاور بازدید نشده از S گره C است. آن را به عنوان بازدید شده نشانه‌گذاری کرده و در صف قرار می‌دهیم.
6		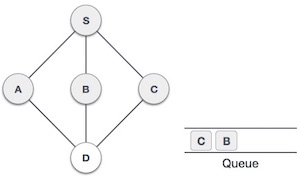اینک S گره مجاور بازدید نشده‌ای ندارد. بنابراین مقادیر آخر را از صف خارج کرده و رأس A را پیدا می‌کنیم.
7		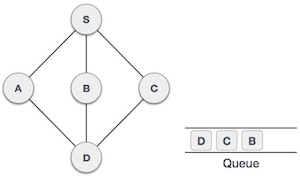از رأس A رأس D را به عنوان گره بازدید نشده مجاور داریم. آن را به صورت بازدید شده نشانه‌گذاری کرده و در صف قرار می‌دهیم.

در این مرحله هیچ گره بازدید نشده بدون نشانه‌گذاری نمانده است. اما بنا بر الگوریتم، باید همه مقادیر صف را خارج کنیم تا همه گره‌های بازدید نشده را پیدا کنیم. وقتی صف خالی شود، برنامه پایان یافته است.

پیاده‌سازی الگوریتم جستجوی سطح-اول در زبان C

در ادامه پیاده‌سازی کد C مثالی که در بخش قبلی بررسی کردیم را مشاهده می‌کنید.

#include 
#include 
#include 

#define MAX 5

struct Vertex {
   char label;
   bool visited;
};

//queue variables

int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;

//graph variables

//array of vertices
struct Vertex* lstVertices[MAX];

//adjacency matrix
int adjMatrix[MAX][MAX];

//vertex count
int vertexCount = 0;

//queue functions

void insert(int data) {
   queue[++rear] = data;
   queueItemCount++;
}

int removeData() {
   queueItemCount--;
   return queue[front++]; 
}

bool isQueueEmpty() {
   return queueItemCount == 0;
}

//graph functions

//add vertex to the vertex list
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

//add edge to edge array
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//display the vertex
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       

//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;
	
   for(i = 0; i<vertexCount; i++) { if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
         return i;
   }
	
   return -1;
}

void breadthFirstSearch() {
   int i;

   //mark first node as visited
   lstVertices[0]->visited = true;

   //display the vertex
   displayVertex(0);   

   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;

   while(!isQueueEmpty()) {
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();   

      //no adjacent vertex found
      while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
		
   }   

   //queue is empty, search is complete, reset the visited flag        
   for(i = 0;i<vertexCount;i++) { lstVertices[i]->visited = false;
   }    
}

int main() {
   int i, j;

   for(i = 0; i<MAX; i++) // set adjacency {
      for(j = 0; j<MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;
   }

   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4
 
   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D
	
   printf("\nBreadth First Search: ");
   
   breadthFirstSearch();

   return 0;
}

اگر کد فوق را کامپایل و اجرا کنیم، نتیجه زیر حاصل می‌آید:

خروجی

Breadth First Search: S A B C D

بدین ترتیب این راهنما با موضوع معرفی گراف به عنوان یک ساختار داده و الگوریتم‌های مربوطه به پایان می‌رسد. هر گونه دیدگاه یا پیشنهاد خود را می‌توانید در بخش نظرات، در ادامه با ما و دیگر خوانندگان فرادرس در میان بگذارید.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۱۶ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

tutorialspoint tutorialspoint tutorialspoint

میثم لطفی (+)

«میثم لطفی» در رشته‌های ریاضیات کاربردی و مهندسی کامپیوتر به تحصیل پرداخته و شیفته فناوری است. وی در حال حاضر علاوه بر پیگیری علاقه‌مندی‌هایش در رشته‌های برنامه‌نویسی، کپی‌رایتینگ و محتوای چندرسانه‌ای، در زمینه نگارش مقالاتی با محوریت نرم‌افزار با مجله فرادرس همکاری دارد.