برنامه تشخیص وجود دور در گراف جهت دار — راهنمای کاربردی

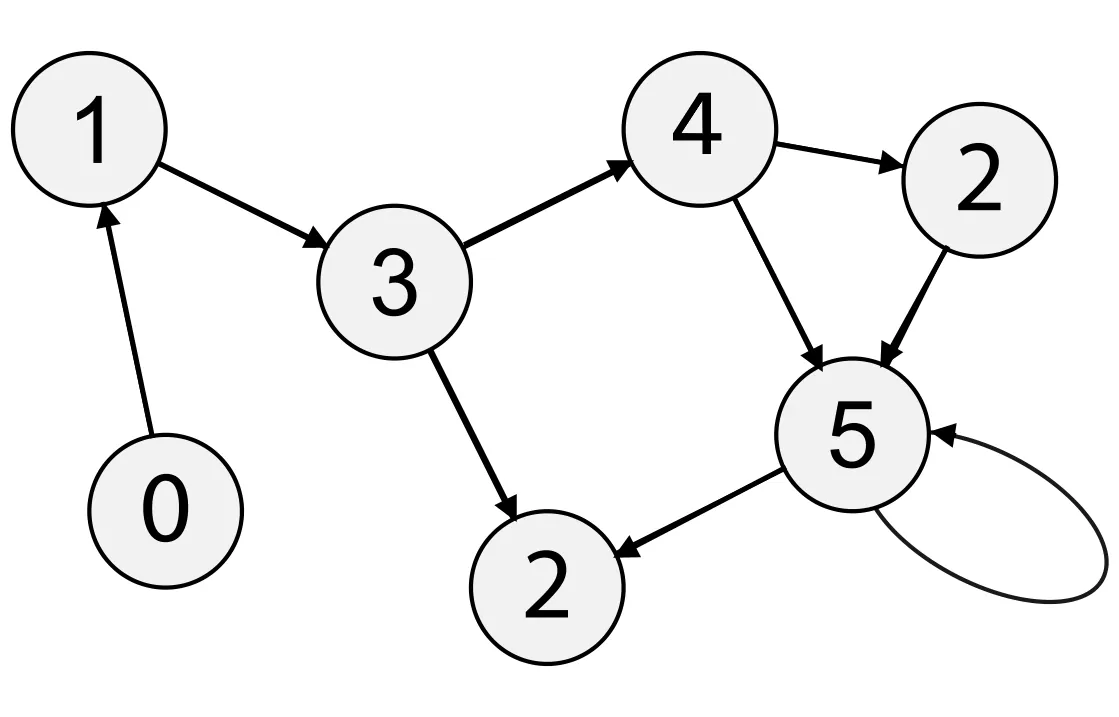
در این مطلب، برنامه تشخیص وجود دور در گراف جهت دار در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java) و «پایتون» (Python) ارائه شده است. همچنین، در مطلب «برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی» نیز به روش تشخیص دور در گراف‌های بدون جهت پرداخته شده است. در ادامه، مساله تشخیص دور در گراف جهت‌دار، همراه با مثالی تشریح می‌شود. یک گراف جهت‌دار (Directed Graph) داده شده است و هدف بررسی این است که آیا گراف دارای دور است یا خیر. تابع باید در صورتی که گراف داده شده حاوی دستکم یک دور باشد مقدار True و در غیر این صورت مقدار False را بازگرداند. برای مثال، گراف زیر دارای سه دور از 0->2->0، 0->1->2->0 و 3->3 است. بنابراین تابع باید مقدار true را باز گرداند. می‌توان از «پیمایش اول عمق» (Depth First Traversal | DFS) برای شناسایی دور در گراف استفاده کرد. DFS برای گراف هم‌بند یک درخت تولید می‌کند. در گراف در صورتی که یال پشتی وجود داشته باشد، دور ایجاد می‌شود. یال پشتی، یالی است که از یک گره به خودش (خود-حلقه‌ای) و یا به والدین خود در درخت تولید شده توسط DFS متصل است. در گرافی که در ادامه می‌آید، سه یال پشتی وجود دارد که با ضرب‌در علامت گذاری شده‌اند. می‌توان مشاهده کرد که ۳ یال پشتی نشانگر ۳ دور نمایش داده شده در گراف هستند.

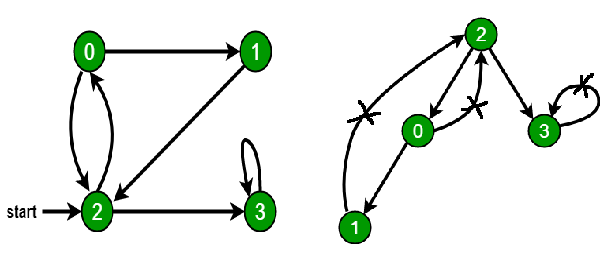
برای یک گراف غیر هم‌بند، جنگل DFS به عنوان خروجی گرفته می‌شود. برای شناسایی دور، می‌توان وجود یک چرخه در درخت‌های مجزا را با بررسی یال پشتی بررسی کرد. برای شناسایی یال پشتی، می‌توان راس‌های موجود در پشته بازگشتی تابع برای پیمایش DFS را دنبال کرد. اگر به راسی رسید که در حال حاضر در پشته بازگشتی قرار دارد، دور در درخت وجود دارد. یالی که راس کنونی را به راس موجود در پشته بازگشتی متصل می‌کند، یال پشتی است. در اینجا، از آرایه []recStack برای پیگیری راس‌ها در پشته بازگشتی استفاده می‌شود.

برنامه تشخیص وجود دور در گراف جهت دار در ++C

// A C++ Program to detect cycle in a graph 
#include<iostream> 
#include <list> 
#include <limits.h> 
  
using namespace std; 
  
class Graph 
{ 
    int V;    // No. of vertices 
    list<int> *adj;    // Pointer to an array containing adjacency lists 
    bool isCyclicUtil(int v, bool visited[], bool *rs);  // used by isCyclic() 
public: 
    Graph(int V);   // Constructor 
    void addEdge(int v, int w);   // to add an edge to graph 
    bool isCyclic();    // returns true if there is a cycle in this graph 
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
    adj = new list<int>[V]; 
} 
  
void Graph::addEdge(int v, int w) 
{ 
    adj[v].push_back(w); // Add w to v’s list. 
} 
  
// This function is a variation of DFSUytil() in https://www.geeksforgeeks.org/archives/18212 
bool Graph::isCyclicUtil(int v, bool visited[], bool *recStack) 
{ 
    if(visited[v] == false) 
    { 
        // Mark the current node as visited and part of recursion stack 
        visited[v] = true; 
        recStack[v] = true; 
  
        // Recur for all the vertices adjacent to this vertex 
        list<int>::iterator i; 
        for(i = adj[v].begin(); i != adj[v].end(); ++i) 
        { 
            if ( !visited[*i] && isCyclicUtil(*i, visited, recStack) ) 
                return true; 
            else if (recStack[*i]) 
                return true; 
        } 
  
    } 
    recStack[v] = false;  // remove the vertex from recursion stack 
    return false; 
} 
  
// Returns true if the graph contains a cycle, else false. 
// This function is a variation of DFS() in https://www.geeksforgeeks.org/archives/18212 
bool Graph::isCyclic() 
{ 
    // Mark all the vertices as not visited and not part of recursion 
    // stack 
    bool *visited = new bool[V]; 
    bool *recStack = new bool[V]; 
    for(int i = 0; i < V; i++) 
    { 
        visited[i] = false; 
        recStack[i] = false; 
    } 
  
    // Call the recursive helper function to detect cycle in different 
    // DFS trees 
    for(int i = 0; i < V; i++) 
        if (isCyclicUtil(i, visited, recStack)) 
            return true; 
  
    return false; 
} 
  
int main() 
{ 
    // Create a graph given in the above diagram 
    Graph g(4); 
    g.addEdge(0, 1); 
    g.addEdge(0, 2); 
    g.addEdge(1, 2); 
    g.addEdge(2, 0); 
    g.addEdge(2, 3); 
    g.addEdge(3, 3); 
  
    if(g.isCyclic()) 
        cout << "Graph contains cycle"; 
    else
        cout << "Graph doesn't contain cycle"; 
    return 0; 
}

برنامه تشخیص وجود دور در گراف جهت دار در جاوا

// A Java Program to detect cycle in a graph 
import java.util.ArrayList; 
import java.util.LinkedList; 
import java.util.List; 
  
class Graph { 
      
    private final int V; 
    private final List<List<Integer>> adj; 
  
    public Graph(int V)  
    { 
        this.V = V; 
        adj = new ArrayList<>(V); 
          
        for (int i = 0; i < V; i++) 
            adj.add(new LinkedList<>()); 
    } 
      
    // This function is a variation of DFSUytil() in  
    // https://www.geeksforgeeks.org/archives/18212 
    private boolean isCyclicUtil(int i, boolean[] visited, 
                                      boolean[] recStack)  
    { 
          
        // Mark the current node as visited and 
        // part of recursion stack 
        if (recStack[i]) 
            return true; 
  
        if (visited[i]) 
            return false; 
              
        visited[i] = true; 
  
        recStack[i] = true; 
        List<Integer> children = adj.get(i); 
          
        for (Integer c: children) 
            if (isCyclicUtil(c, visited, recStack)) 
                return true; 
                  
        recStack[i] = false; 
  
        return false; 
    } 
  
    private void addEdge(int source, int dest) { 
        adj.get(source).add(dest); 
    } 
  
    // Returns true if the graph contains a  
    // cycle, else false. 
    // This function is a variation of DFS() in  
    // https://www.geeksforgeeks.org/archives/18212 
    private boolean isCyclic()  
    { 
          
        // Mark all the vertices as not visited and 
        // not part of recursion stack 
        boolean[] visited = new boolean[V]; 
        boolean[] recStack = new boolean[V]; 
          
          
        // Call the recursive helper function to 
        // detect cycle in different DFS trees 
        for (int i = 0; i < V; i++) 
            if (isCyclicUtil(i, visited, recStack)) 
                return true; 
  
        return false; 
    } 
  
    // Driver code 
    public static void main(String[] args) 
    { 
        Graph graph = new Graph(4); 
        graph.addEdge(0, 1); 
        graph.addEdge(0, 2); 
        graph.addEdge(1, 2); 
        graph.addEdge(2, 0); 
        graph.addEdge(2, 3); 
        graph.addEdge(3, 3); 
          
        if(graph.isCyclic()) 
            System.out.println("Graph contains cycle"); 
        else
            System.out.println("Graph doesn't "
                                    + "contain cycle"); 
    } 
} 
  
// This code is contributed by Sagar Shah.

برنامه تشخیص وجود دور در گراف جهت دار در پایتون

# Python program to detect cycle  
# in a graph 
  
from collections import defaultdict 
  
class Graph(): 
    def __init__(self,vertices): 
        self.graph = defaultdict(list) 
        self.V = vertices 
  
    def addEdge(self,u,v): 
        self.graph[u].append(v) 
  
    def isCyclicUtil(self, v, visited, recStack): 
  
        # Mark current node as visited and  
        # adds to recursion stack 
        visited[v] = True
        recStack[v] = True
  
        # Recur for all neighbours 
        # if any neighbour is visited and in  
        # recStack then graph is cyclic 
        for neighbour in self.graph[v]: 
            if visited[neighbour] == False: 
                if self.isCyclicUtil(neighbour, visited, recStack) == True: 
                    return True
            elif recStack[neighbour] == True: 
                return True
  
        # The node needs to be poped from  
        # recursion stack before function ends 
        recStack[v] = False
        return False
  
    # Returns true if graph is cyclic else false 
    def isCyclic(self): 
        visited = [False] * self.V 
        recStack = [False] * self.V 
        for node in range(self.V): 
            if visited[node] == False: 
                if self.isCyclicUtil(node,visited,recStack) == True: 
                    return True
        return False
  
g = Graph(4) 
g.addEdge(0, 1) 
g.addEdge(0, 2) 
g.addEdge(1, 2) 
g.addEdge(2, 0) 
g.addEdge(2, 3) 
g.addEdge(3, 3) 
if g.isCyclic() == 1: 
    print "Graph has a cycle"
else: 
    print "Graph has no cycle"
  
# Thanks to Divyanshu Mehta for contributing this code

خروجی

Graph contains cycle

پیچیدگی زمانی این روش، مشابه با پیچیدیگی زمانی پیمایش DFS و برابر با (O(V+E است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^