جواب تکین معادلات دیفرانسیل — از صفر تا صد
در آموزشهای قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزشها، روشهای حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله دیفرانسیل چبیشف پرداختیم. در این آموزش، یکی از مباحث مربوط به معادلات دیفرانسیل، یعنی جواب تکین را معرفی و روش به دست آوردن آن را بیان میکنیم.
تعریف جواب تکین
تابع $$\varphi (x)$$ را «جواب تکین» (Singular Solution) معادله دیفرانسیل $$F(x,y,y^ \prime)=0$$ مینامیم، هرگاه یکتایی جواب در هر نقطه از دامنه معادله نقض شود. از نظر هندسی، این بدین معنی است که بیش از یک منحنی، با خط مماس مشترک از هر نقطهای مثل $$(x_0,y_0)$$ عبور میکند.
نکته: گاهی هنگامی که یکتایی جواب معادله دیفرانسیل ممکن است فقط در برخی نقاط نقض شود، از تعریف ضعیفتر جواب تکین استفاده میشود.
جواب تکین معادله دیفرانسیل توسط انتگرال عمومی (معمولی) توصیف نمیشود، یعنی نمیتوان به ازای هیچ مقدار خاصی از ثابت $$C$$ از جواب عمومی مشتق گرفت. این موضوع را با مثال زیر روشن میکنیم.
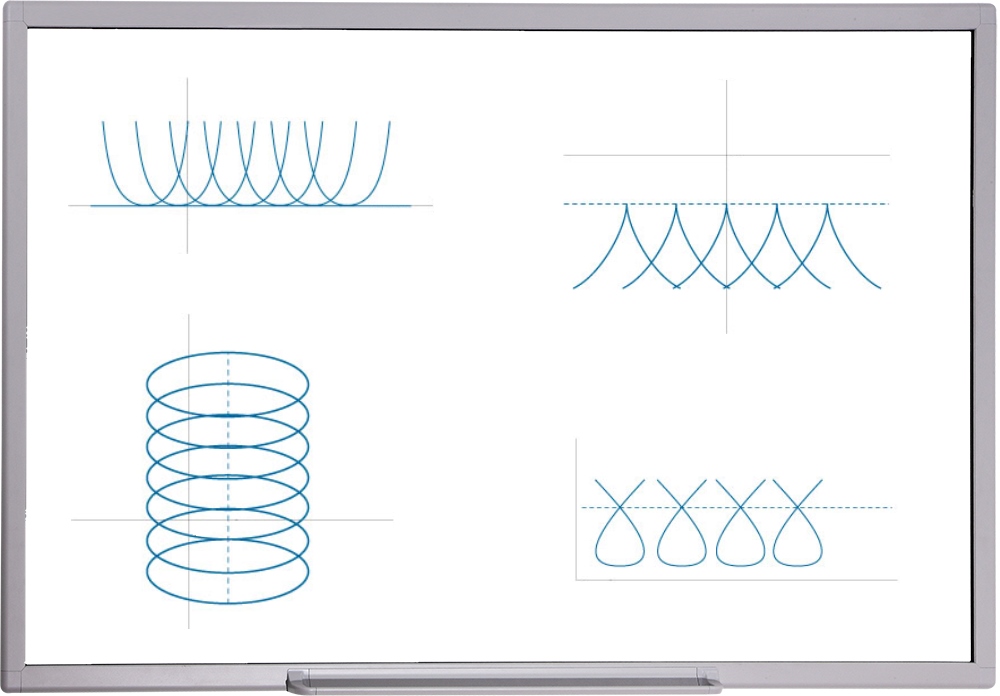
فرض کنید معادلهای به شکل $$ {\left( {y’} \right)^2} – 4y = 0 $$ را باید حل کنیم. این معادله را میتوان به راحتی حل کرد. جواب عمومی این معادله تابعی به صورت $$y=(x+C)^2$$ است. از نظر هندسی، این تابع توسط دستهای از سهمیها نمایش داده میشود (شکل 1).
علاوه بر این، تابع $$y=0$$ نیز در این معادله دیفرانسیل صدق میکند. اما، جواب عمومی شامل این تابع نیست. از آنجایی که بیش از یک منحنی کامل از هر نقطه از خط راست $$y=0$$ میگذرد، یکتایی جواب روی این خط نقض میشود و از این رو، جواب تکین این معادله دیفرانسیل است.
مبیّن $$\Large{p}$$
یکی از روشهای یافتن جواب تکین، بررسی مبیّن $$p$$ معادله دیفرانسیل است. اگر تابع $$ F\left( {x,y,y’} \right) $$ و مشتقات جزئی آن $$ {\large\frac{{\partial F}}{{\partial y}}\normalsize}, {\large\frac{{\partial F}}{{\partial y’}}\normalsize} $$ در دامنه معادله دیفرانسیل پیوسته باشند، جواب تکین را میتوان از مجموعه معادلات زیر به دست آورد:
$$ \large \left \{ \begin {array} {l}
F \left ( { x , y , y ’ } \right ) = 0 \\
\frac { { \partial F \left ( { x , y , y ’ } \right ) } } { { \partial y ’ } } = 0
\end {array} \right . . $$
با حل مجموعه معادلات بالا، معادلهای به صورت $$ \psi \left( {x,y} \right) = 0$$ به دست میآید که مبین $$p$$ این معادله دیفرانسیل نامیده میشود و منحنی متناظر با آن را منحنی مبین $$p$$ مینامند.
با به دست آوردن منحنی مبین $$p$$، باید آن را به صورت زیر بررسی کرد:
- آیا جواب به دست آمده، جواب معادله دیفرانسیل است؟
- آیا این جواب، یک جواب تکین است؛ یعنی آیا در اینجا منحنیهای کامل دیگری در این معادله دیفرانسیل وجود دارد که با منحنی مبین $$p$$ در هر نقطهای تماس پیدا کند؟
برای این کار، کافی است مراحل زیر را انجام دهید:
- جواب عمومی معادله دیفرانسیل را بیابید (آن را $$y_1$$ بنامید)؛
- شرطهای تماس جواب تکین (آن را با $$y_2$$ مشخص کنید) و جواب عمومی $$y_1$$ را در نقطه دلخواه $$x_0$$ بنویسید:
$$ \large \left \{ \begin {array} {l}
{ y _ 1 } \left ( { { x _ 0 } } \right ) = { y _ 2 } \left( { { x _ 0 } } \right ) \\
{ y ’ _ 1 } \left ( { { x _ 0 } } \right ) = { y ’ _ 2 } \left ( { { x _ 0 } } \right )
\end {array} \right . ; $$
اگر این شرطها در نقطه دلخواه $$x_0$$ یک جواب داشته باشند، تابع $$y_2$$ یک جواب تکین است. جواب تکین معمولاً متناظر با پوش دسته منحنیهای کامل جواب عمومی معادله دیفرانسیل است.
پوش دسته منحنیهای کامل و مبین $$\Large$$
روش دیگر به دست آوردن جواب تکین به عنوان پوش دسته منحنیهای کامل، استفاده از مبین $$C$$ است.
فرض کنید $$ \Phi \left( {x,y,C} \right) $$ جواب عمومی معادله دیفرانسیل $$ F\left( {x,y,y’} \right) = 0 $$ باشد. از لحاظ هندسی معادله $$ \Phi \left( {x,y,C} \right) = 0 $$ متناظر با دسته منحنیهای کامل در صفحه $$xy$$ است. اگر تابع $$ \Phi \left( {x,y,C} \right) $$ و مشتقات جزئی آن پیوسته باشند، پوش دسته منحنیهای کامل جواب عمومی توسط مجموعه معادلات زیر تعریف میشود:
$$ \large \left\{ \begin {array} {l}
\Phi \left ( { x , y , C } \right ) = 0 \\
\frac { { \partial \Phi \left ( { x , y , C } \right ) } } { { \partial C } } = 0
\end {array} \right . . $$
برای اینکه مطمئن شویم آیا جواب این مجموعه معادلات واقعاً پوش است، میتوانیم از روشی استفاده کنیم که در بخش قبلی گفته شد.
روش کلی یافتن نقاط تکین
یک روش رایجتر برای یافتن نقاط تکین یک معادله دیفرانسیل، استفاده همزمان از مبین $$p$$ و $$C$$ است.
در اینجا، ابتدا معادلات مبین $$p$$ و $$C$$ را به دست میآوریم:
- $$ {\psi_p}\left( {x,y} \right) = 0$$ معادله مبین $$p$$،
- و $$ {\psi_C}\left( {x,y} \right) = 0 $$ معادله مبین $$C$$ است.
این معادلات ساختار معینی دارند. در حالت کلی، معادله مبین $$p$$ را میتوان به صورت ضرب سه تابع نوشت:
$$ \large { { \psi _ p } \left ( { x , y } \right ) } = { E \times { T ^ 2 } \times C } = { 0 , } $$
که در آن، $$E$$ معادله پوش، $$T$$ معادله مکان هندسی نقاط غیرمتوالی و $$C$$ معادله مکان هندسی نقطه بازگشت است.
به طور مشابه، معادله مبین $$C$$ را نیز میتوان به صورت ضرب سه تابع نوشت:
$$ \large { { \psi _ C } \left ( { x , y } \right ) } = { E \times { N ^ 2 } \times { C ^ 3 } } = { 0 , } $$
در این معادله، $$E$$ معادله پوش، $$N$$ معادله مکان هندسی گره و $$C$$ معادله مکان هندسی نقطه بازگشت است.
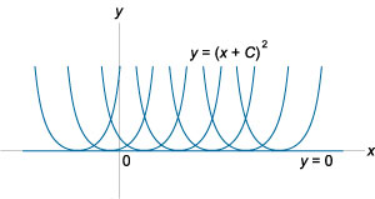
در اینجا با انواع جدیدی از نقاط تکین شامل مکان هندسی نقطه بازگشت ($$C$$)، مکان هندسی نقاط غیرمتوالی ($$T$$) و مکان هندسی گره ($$N$$) مواجه میشویم. در شکلهای ۲ تا ۴، این نقاط در صفحه $$xy$$ نشان داده شدهاند.
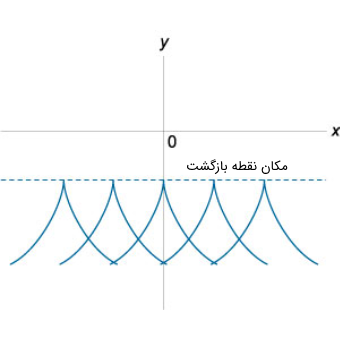
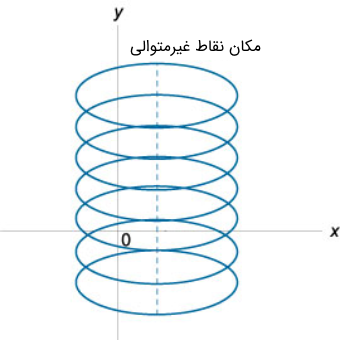
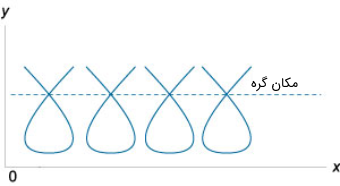
سه نوع از این چهار نقطه، یعنی مکان هندسی نقاط غیرمتوالی، نقطه بازگشت و گره، نقاط خارجی هستند؛ یعنی در معادله دیفرانسیل صدق نمیکنند و از این رو، جوابهای تکین معادله دیفرانسیل نیستند. فقط پوش نقاط مورد نظر جواب تکین است. از آنجایی که در معادلات مبین $$p$$ و $$C$$، پوش به عنوان عامل درجه اول معرفی شده است، به دست آوردن معادله پوش امکانپذیر خواهد بود.
مثالها
در ادامه، چند مثال را بررسی میکنیم.
مثال ۱
جوابهای تکین معادله $$ 1 + { \left ( { y ’ } \right ) ^ 2 }= {\frac{1}{{{y^2}}}\normalsize} $$ را بیابید.
حل: برای بررسی نقاط تکین، از مبین $$p$$ استفاده میکنیم. با مشتق گرفتن از معادله نسبت به $$y’ $$ داریم:
$$ \large 2 y ’ = 0 , \; \; \Rightarrow y ’ = 0 . $$
با قرار دادن این رابطه در معادله دیفرانسیل، معادله مبین $$p$$ به دست میآید:
$$ \large 1 + 0 = \frac { 1 } { { { y ^ 2 } } } . $$
از این رابطه نتیجه میگیریم که معادله مبین $$p$$، دو خط افقی $$ y = \pm 1 $$ را توصیف میکند. اکنون باید نشان دهیم که این جواب در معادله دیفرانسیل صدق میکند:
$$ \large { y = \pm 1 , \; \; } \Rightarrow { y ’ = 0 , \; \; } \Rightarrow
{ 1 + { 0 ^ 2 } = \frac { 1 } { { { 1 ^ 2 } } } , \; \; } \Rightarrow
{ 1 = 1 . } $$
جواب عمومی معادله دیفرانسیل را به صورت زیر به دست میآوریم:
$$ \large { { { \left ( { y ’ } \right ) ^ 2 } = \frac { 1 } { { { y ^ 2} } } – 1 } = { \frac { { 1 – { y ^ 2 } } }{ { { y ^ 2 } } } , \; \; } } \\ \large \Rightarrow
{ y ’ = \pm \frac { { \sqrt { 1 – { y ^ 2 } } } } { y } , \; \; } \Rightarrow
{ \frac { { y d y} } { { \sqrt { 1 – { y ^ 2 } } } } = \pm d x . } $$
با استفاده از تغییر متغیر داریم:
$$ \large { 1 – { y ^ 2 } = t , \; \; } \Rightarrow { – 2 y d y = d t , \; \; } \Rightarrow
{ y d y = – \frac { { d t } } { 2 } . } $$
در نتیجه، خواهیم داشت:
$$ \large \frac { { \left ( { – \frac { { d t } } { 2 } } \right ) } } { { \sqrt t } } = \pm d x . $$
پس از انتگرالگیری، جواب عمومی معادله دیفرانسیل به شکل زیر خواهد بود:
$$ \large { \int { \frac { { d t } } { { 2 \sqrt t } } } = \pm \int { d x } , \; \; } \Rightarrow
{ \sqrt t = \pm x + C , \; \; } \\ \large\Rightarrow
{ \sqrt { 1 – { y ^ 2 } } = \pm \left ( { x + C } \right ) , } $$
که در آن، $$C$$ یک ثابت اختیاری است.
جواب به دست آمده را میتوان اینگونه نوشت:
$$ \large { \left ( { x + C } \right ) ^ 2 } + { y ^ 2 } = 1 . $$
این معادله، دسته دایرههایی را با شعاع $$1$$ در بازه $$ -1 \le y \le 1 $$ توصیف میکند (شکل 5). همان گونه که در شکل دیده میشود، خطوط مبین $$p$$، $$ y = \pm 1$$ پوشهای دایرههای مفروض هستند. اما، باید صریحاً ثابت کنیم که یکتایی جواب روی این خطوط راست نقض میشود.
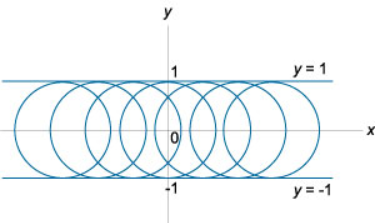
برای این کار ابتدا شرط تماس دو منحنی کامل را در نقطه دلخواه $$x_0$$ مینویسیم:
$$ \large \left\{ \begin {array} {l}
{ y _ 1 } \left ( { { x _ 0 } } \right ) = { y _ 2 } \left ( { { x _ 0 } } \right ) \\
{ y ’ _ 1 } \left ( { { x _ 0 } } \right ) = { y ’ _ 2 } \left ( { { x _ 0 } } \right )
\end {array} \right . . $$
اینجا $$y_1(x)$$ جواب عمومی معادله است که برای نیمدایره بالایی به این صورت است:
$$ \large { { y _ 1 } \left ( x \right ) } = { \sqrt { 1 – { { \left ( { x + C } \right ) } ^ 2 } } . } $$
تابع $$y_2(x)$$ متناظر با خط افقی $$y=1$$ است. برای اینکه هر دو خط در نقطه $$x_0$$ تماس پیدا کنند، باید روابط زیر برقرار باشد:
$$ \large \left\{ \begin {array} {l}
\sqrt { 1 – { { \left ( { { x _ 0 } + C } \right ) } ^ 2 } } = 1 \\
\frac { { – { x _ 0 } – C } } { { \sqrt { 1 – { x _ 0 } + C } } } = 0
\end {array} \right . . $$
از این معادلات میتوان نتیجه گرفت که شرط تماس هر دو خط در نقطه $$x_0$$ این است که $$C=x_0$$ باشد.
بنابراین، ثابت کردیم که در هر نقطه $$x_0$$ روی خط مستقیم $$y=1$$ به ازای $$C=-x_0$$ یک تماس دایرهای وجود دارد. از این رو، یکتایی جواب در هر نقطه از خط راست نقض میشود. بنابراین، خط $$y=1$$ جواب تکین معادله دیفرانسیل است. به طور مشابه، میتوانیم ثابت کنیم که خط $$y=-1$$ نیز یک جواب تکین است.
مثال ۲
جواب تکین معادله دیفرانسیل $$ y = { \left ( { y ’ } \right ) ^ 2 } $$ را به دست آورید. جواب عمومی معادله، تابعی به صورت $$ y = C x + { C ^ 2 } $$ است.
حل: برای تعیین جواب تکین از مبین $$C$$ استفاده میکنیم. از آنجایی که جواب عمومی معادله دیفرانسیل معلوم است، میتوان نوشت:
$$ \large { \Phi \left ( { x , y , C } \right ) \text { = } } \kern0pt{ y – C x – { C ^ 2 } – { x ^ 2 } . } $$
از این معادله نسبت به $$C$$ مشتق جزئی میگیریم:
$$ \large { \frac { { \partial \Phi \left ( { x , y , C } \right ) } }{ { \partial C } } } = { – x – 2 C . } $$
بنابراین، مجموعه معادلاتی به صورت زیر خواهیم داشت:
$$ \large \left\{ \begin {array} {l}
y = C x – { C ^ 2 } – { x ^ 2 } \\
– x – 2 C = 0
\end {array} \right . . $$
از معادله دوم نتیجه میگیریم که $$ C = – {\large\frac{x}{2}\normalsize} $$ است. با جایگذاری این مقدار در معادله اول، منحنی مبین $$C$$ به دست میآید که یک سهمی است:
$$ \large { y = \left ( { – \frac { x } { 2 } } \right ) \cdot x } - { { \left ( { – \frac { x } { 2 } } \right ) ^ 2 } } - { { x ^ 2 } }
= { \frac { 3 } { 4 } { x ^ 2 } . } $$
برای اینکه اطمینان پیدا کنیم این تابع جواب معادله دیفرانسیل اصلی است، کافی است آن را در معادله قرار دهیم:
$$ \large { y = \frac { 3 } { 4 } { x ^2 } , \; \; } \Rightarrow
{ y ’ = \frac { 3 } { 2 } x , \; \; } \\ \large \Rightarrow
{ { \frac { 3 } { 4 }{ x ^ 2 } = { \left ( { \frac { 3 } { 2 } x } \right ) ^ 2 } } - { 3 x \cdot \frac { 3 } { 2 } x + 3 { x ^ 2 } , \; \; } } \\ \large \Rightarrow
{ { \frac { 3 } { 4 } { x ^ 2 } = \frac { 9 } { 4 } { x ^ 2 } } - { \frac { 9 } { 2 } { x ^ 2 } + 3 { x ^ 2 } , \; \; } } \Rightarrow
{ \frac { 3 } { 4 } { x ^ 2 } = \frac { 3 } { 4 } { x ^ 2 } . } $$
اکنون بررسی میکنیم که یکتایی جواب روی این منحنی نقض میشود. ابتدا تابع $$y_1$$ را مشخص میکنیم:
$$ \large { { y _ 1 } = C x + { C ^ 2 } + { x ^ 2 } , \; \; } \kern-0.3pt { { y _ 2 } = \frac { 3 } { 4 } { x ^ 2 } . } $$
شرطهای تماس دو منحنی را در نقطه دلخواه $$x_0$$ مینویسیم:
$$ \large \left\{ \begin {array} {l}
{ y _ 1 } \left ( { { x _ 0 } } \right ) = { y _ 2 } \left ( { { x _ 0 } } \right) \\
{ y ’ _ 1 } \left ( { { x _ 0 } } \right ) = { y ’ _ 2 } \left ( { { x _ 0 } } \right )
\end {array} \right . . $$
داریم:
$$ \large \left\{ \begin {array} {l}
C { x _ 0 } + { C ^ 2 } + x _ 0 ^ 2 = \frac { 3 } { 4 } x _ 0 ^ 2 \\
C + 2 { x _ 0 } = \frac { 3 } { 2 } { x _ 0 }
\end {array} \right . . $$
اگر ثابت $$C$$ در هر نقطه $$x_0$$ برابر با $$C = – \frac{{{x_0}}}{2}$$ باشد، این معادلات سازگار هستند.
بنابراین، ثابت کردیم که منحنی مبین $$C$$، $$y = {\large\frac{3}{4}\normalsize}{x^2}$$، پوش (جواب تکین) دسته سهمیهای $$y = Cx+\,{C^2} + {x^2}$$ است.
مثال ۳
جوابهای تکین معادله دیفرانسیل $$ {\left( {y’} \right)^2}{\left( {1 – y} \right)^2}= 2 – y $$ را بررسی کنید.
حل: ابتدا مبین $$p$$ معادله را به دست میآوریم. از این معادله نسبت به $$x$$ مشتق میگیریم:
$$ \large 2 y ’ { \left( { 1 – y } \right) ^ 2 } = 0 . $$
عبارت $$ y’$$ را از مجموعه معادلات زیر حذف میکنیم:
$$ \large \left\{ \begin {array} {l}
{ \left( { y ’ } \right) ^ 2 } { \left( { 1 – y } \right) ^ 2 } = 2 – y \\
y ’ { \left( { 1 – y } \right) ^ 2 } = 0
\end {array} \right . . $$
بنابراین، داریم:
$$ \large {{\left( {y’} \right)^2} = \frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}},\;\;}\Rightarrow
{\frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}} \cdot {\left( {1 – y} \right)^4} = 0,\;\;}\Rightarrow
{{\left( {1 – y} \right)^2}\left( {2 – y} \right) = 0.} $$
اکنون مبین $$C$$ را تعیین میکنیم. برای پیدا کردن این مبین به حل معادله دیفرانسیل و به دست آوردن جواب عمومی آن نیاز داریم. معادله را به صورت زیر بازنویسی میکنیم:
$$ \large {{\left( {\frac{{dy}}{{dx}}} \right)^2} = \frac{{2 – y}}{{{{\left( {1 – y} \right)}^2}}},\;\;}\Rightarrow
{\frac{{dy}}{{dx}} = \pm \frac{{\sqrt {2 – y} }}{{1 – y}},\;\;}\\ \large \Rightarrow
{\frac{{\left( {1 – y} \right)dy}}{{\sqrt {2 – y} }} = \pm dx.} $$
با انتگرالگیری از طرفین داریم:
$$ \large {\int {\frac{{\left( {1 – y} \right)dy}}{{\sqrt {2 – y} }}} }={ \pm \int {dx} + C.} $$
برای حل انتگرال سمت چپ از تغییر متغیر استفاده میکنیم:
$$ \large {2 – y = t,\;\; }\Rightarrow {dy = – dt,\;\;}\Rightarrow {1 – y = t – 1.} $$
خواهیم داشت:
$$ \large {{\int {\frac{{\left( {t – 1} \right)\left( { – dt} \right)}}{{\sqrt t }}} }={ \pm x + C,\;\;}}\Rightarrow
{{\int {\left( {\sqrt t – \frac{1}{{\sqrt t }}} \right)dt} }={ \mp x – C,\;\;}}\\ \large \Rightarrow
{{\frac{{{t^{\large\frac{3}{2}\normalsize}}}}{{\frac{3}{2}}} – \frac{{{t^{\large\frac{1}{2}\normalsize}}}}{{\frac{1}{2}}} }={ \mp x – C,\;\;}}\Rightarrow
{{\frac{2}{3}{t^{\large\frac{3}{2}\normalsize}} – 2{t^{\large\frac{1}{2}\normalsize}} }={ \mp x – C,\;\;}} \\ \large \Rightarrow
{{\frac{2}{3}{\left( {2 – y} \right)^{\large\frac{3}{2}\normalsize}} }-{ 2{\left( {2 – y} \right)^{\large\frac{1}{2}\normalsize}} }={ \mp x – C,\;\;}}\Rightarrow
{{\frac{2}{3}\sqrt {2 – y} \left( {2 – y – 3} \right) }={ \mp x – C,\;\;}} \\ \large \Rightarrow
{{\frac{4}{9}\left( {2 – y} \right){\left( {y + 1} \right)^2} }={ {\left( {x + C} \right)^2},\;\;}}\Rightarrow
{{4\left( {2 – y} \right){\left( {y + 1} \right)^2} }={ 9{\left( {x + C} \right)^2}.}} $$
از جواب عمومی نسبت به $$C$$ مشتق میگیریم:
$$ \large 0 = 18\left( {x + C} \right). $$
با قرار دادن $$ x + C = 0 $$ در جواب عمومی، معادله مبین $$C$$ را به دست میآوریم:
$$ \large {\left( {y + 1} \right)^2}\left( {2 – y} \right) = 0. $$
اکنون میتوانیم معادلات مبین $$p$$ و $$C$$ را با هم بنویسیم:
$${{\psi _p}\left( y \right) }={ {\left( {1 – y} \right)^2}\left( {2 – y} \right) }={ 0,} \\ \large
{{\psi _C}\left( y \right) }={ {\left( {y + 1} \right)^2}\left( {2 – y} \right) }={ 0.} $$
از ساختار این معادلات نتیجه گرفته میشود که معادله $$2-y=0$$ معادله پوش است، زیرا در هر دو معادله، عامل درجه اول است. همچنین میتوانیم معادله مکان هندسی نقاط غیرمتوالی را از معادله مبین $$p$$ به دست آوریم:
$$ \large {{\left( {1 – y} \right)^2} = 0,\;\; }\Rightarrow {y = 1.} $$
و به طور مشابه، از معادله مبین $$C$$ نتیجه میگیریم که معادله مکان هندسی گره به صورت زیر است:
$$ \large {{\left( {y + 1} \right)^2} = 0,\;\; }\Rightarrow {y = – 1.} $$
در این مثال، فقط پوش $$y=2$$ جواب تکین معادله دیفرانسیل است.










