معادله دیفرانسیل چبیشف — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، درباره معادلات دیفرانسیل بحث و روش‌های حل معادلات دیفرانسیل مرتبه دوم را بررسی کردیم. «معادله دیفرانسیل چبیشف» (Chebyshev Differential Equation)‌ نوع خاصی از معادلات دیفرانسیل مرتبه دوم است که در این آموزش به آن می‌پردازیم.

معادله دیفرانسیل به‌فرم زیر را «معادله چبیشف» (Chebyshev equation) می‌نامند:

 $${\left( {1 – {x^2}} \right)y^{\prime\prime} – xy’ }+{ {n^2}y }={ 0}$$

که در آن، $$\left| x \right| \lt 1$$ و $$n$$ یک عدد حقیقی است. نام این معادله، از اسم ریاضی‌دان مشهور روسی «پافنوتی چبیشف» (Pafnuty Chebyshev) گرفته شده است.

معادله چبیشف را می‌توان با استفاده از تبدیل $$x = \cos t$$ به یک فرم ساده‌تر نوشت. با تبدیل مذکور داریم:

$${x = \cos t,\;\; }\Rightarrow {dx = – \sin tdt,\;\;}
\Rightarrow {\frac{{dt}}{{dx}} = – \frac{1}{{\sin t}}.}$$

بنابراین:

$${y’ = \frac{{dy}}{{dx}} = \frac{{dy}}{{dt}}\frac{{dt}}{{dx}} }={ – \frac{1}{{\sin t}}\frac{{dy}}{{dt}},}$$

$${y^{\prime\prime} = \frac{{{d^2}y}}{{d{x^2}}} = \frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) }
= {\frac{d}{{dt}}\frac{{dt}}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) } \\
= { – \frac{1}{{\sin t}}\frac{d}{{dt}}\left( { – \frac{1}{{\sin t}}\frac{{dy}}{{dt}}} \right) } \\
= {{\frac{1}{{\sin t}}\left[ {\frac{d}{{dt}}\left( {\frac{1}{{\sin t}}} \right)\frac{{dy}}{{dt}} }\right.}+{\left.{ \frac{1}{{\sin t}}\frac{{{d^2}y}}{{d{t^2}}}} \right] }} \\
= {{\frac{1}{{\sin t}}\left[ {\left( { – \frac{{\cos t}}{{{{\sin }^2}t}}} \right)\frac{{dy}}{{dt}} }\right.}+{\left.{ \frac{1}{{\sin t}}\frac{{{d^2}y}}{{d{t^2}}}} \right] }} \\
= {{\frac{1}{{{{\sin }^2}t}}\left[ {\left( { – \frac{{\cos t}}{{\sin t}}} \right)\frac{{dy}}{{dt}} }\right.}+{\left.{ \frac{{{d^2}y}}{{d{t^2}}}} \right].}}$$

با جایگذاری عبارات مشتق در معادله دیفرانسیل، می‌توان نوشت:

$$\require{cancel}
{\left( {1 – {{\cos }^2}t} \right)\frac{1}{{{{\sin }^2}t}} \cdot}\kern0pt{ \left[ {\left( { – \frac{{\cos t}}{{\sin t}}} \right)\frac{{dy}}{{dt}} + \frac{{{d^2}y}}{{d{t^2}}}} \right] }
– {\cos t\left[ { – \frac{1}{{\sin t}}\frac{{dy}}{{dt}}} \right] }+{ {n^2}y = 0,\;\;}\\
\Rightarrow
{{\frac{\cancel{{{\sin }^2}t}}{\cancel{{{\sin }^2}t}}\left[ { – \frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}} + \frac{{{d^2}y}}{{d{t^2}}}} \right] }+{ \frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}} + {n^2}y = 0,\;\;}}\\
\Rightarrow
{{ – \cancel{\frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}}} + \frac{{{d^2}y}}{{d{t^2}}} }+{ \cancel{\frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}}} + {n^2}y = 0.}}$$

در نتیجه، معادله دیفرانسیل چبیشف به فرم فشرده زیر در می‌آید:

$$\frac{{{d^2}y}}{{d{t^2}}} + {n^2}y = 0.$$

جواب عمومی معادله اخیر با فرمول زیر بیان می‌شود:

$${y\left( t \right) }={ {C_1}\cos \left( {nt} \right) + {C_2}\sin\left( {nt} \right)}$$

که می‌توان آن را به‌فرم زیر نوشت:

$$y\left( t \right) = C\cos \left( {nt + \alpha } \right).$$

در معادله بالا، $$C_1$$، $$C_2$$، $$C$$ و $$\alpha$$ اعداد حقیقی اختیاری هستند. برای سادگی، می‌توان $$\alpha =0$$ را در نظر گرفت. در نتیجه، جواب عمومی معادله چبیشف با فرمول زیر بیان می‌شود:

$$y\left( x \right) = C\cos \left( {n\arccos x} \right).$$

در عبارت بالا، $$n$$ ممکن است هر عدد حقیقی باشد. اما اگر $$n$$ یک عدد صحیح باشد، تابع فوق، چندجمله‌ای چبیشف نوع اول خواهد بود.

چندجمله‌ای چبیشف نوع اول

تابع زیر را چندجمله‌ای چبیشف نوع اول می‌نامند:

$${T_n}\left( x \right) = \cos \left( {n\arccos x} \right),$$

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد در فرادرس

کلیک کنید

که در آن، $$\left| x \right| \le 1$$ و $$n = 0,1,2,3, \ldots$$. در ادامه نشان می‌دهیم که این تابع واقعاً یک چندجمله‌ای جبری است. برای $$n=0$$ و $$n=1$$ داریم:

$${T_0}\left( x \right) = \cos 0 = 1,$$

$${{T_1}\left( x \right) = \cos \left( {\arccos x} \right) }={ x.}$$

با قرار دادن $$x = \cos t$$، می‌توانیم روابط زیر را بنویسیم:

$${{T_1}\left( t \right) }={ \cos \left( {\arccos \left( {\cos t} \right)} \right) }={ \cos t,}$$

$${{T_n}\left( t \right) }={ \cos \left( {n\arccos \left( {\cos t} \right)} \right) }={ \cos \left( {nt} \right),}$$

$${{T_{n – 1}}\left( t \right) }={ \cos \left( {\left( {n – 1} \right)\arccos \left( {\cos t} \right)} \right) }={ \cos \left( {\left( {n – 1} \right)t} \right),}$$

$${{T_{n + 1}}\left( t \right) }={ \cos \left( {\left( {n + 1} \right)\arccos \left( {\cos t} \right)} \right) }={ \cos \left( {\left( {n + 1} \right)t} \right).}$$

از آن‌جایی که

$${\cos \left( {\left( {n – 1} \right)t} \right) + \cos \left( {\left( {n + 1} \right)t} \right) } \\
= {2\cos \frac{{\left( {n – 1} \right)t + \left( {n + 1} \right)t}}{2} \cdot}\kern0pt{ \cos \frac{{\left( {n – 1} \right)t – \left( {n + 1} \right)t}}{2} } \\
= {2\cos \frac{{2nt}}{2}\cos \frac{{\left( { – 2t} \right)}}{2} } \\
= {2\cos \left( {nt} \right)\cos t}$$

می‌توانیم رابطه بازگشتی زیر را برای چندجمله‌ای چبیشف نوع اول به‌دست آوریم:

$${{T_{n – 1}} + {T_{n + 1}} = 2{T_n}{T_1},\;\;}\\
\Rightarrow {{T_{n + 1}} = 2{T_n}x – {T_{n – 1}}.}$$

اکنون، چندجمله‌ای‌های چبیشف مرتبه بالاتر نیز به‌سادگی قابل محاسبه است:

$${{T_2} = 2{T_1}\left( x \right)x – {T_0} }={ 2{x^2} – 1,}$$

$${{T_3} = 2{T_2}\left( x \right)x – {T_1} }
= {2\left( {2{x^2} – 1} \right)x – x }
= {4{x^3} – 3x,}$$

$${{T_4} = 2{T_3}\left( x \right)x – {T_2} }
= {2\left( {4{x^3} – 3x} \right)x }-{ \left( {2{x^2} – 1} \right) }
= {8{x^4} – 8{x^2} + 1,}$$

$${{T_5} = 2{T_4}\left( x \right)x – {T_3} }
= {2\left( {8{x^4} – 8{x^2} + 1} \right)x }-{ \left( {4{x^3} – 3x} \right) }
= {16{x^5} – 20{x^3} + 5x,}$$

$$\vdots$$

چندجمله‌ای چبیشف نوع دوم

چندجمله‌ای‌های چبیشف نوع دوم را می‌توان به شکل بازگشتی زیر نوشت:

$${{U_n}\left( x \right) \text{ = }}\kern0pt
{\begin{cases}
1, \text{ if }n = 0 \\
2x, \text{ if }n = 1 \\
{2x{U_{n – 1}}\left( x \right) – {U_{n – 2}}\left( x \right),}\kern0pt{ \text{ if }n \le 2}
\end{cases}}$$

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

چندجمله‌ای‌های چبیشف نوع دوم، جواب معادله دیفرانسیل چبیشف زیر هستند:

$${\left( {1 – {x^2}} \right)y^{\prime\prime} – 3xy’ }+{ n\left( {n + 2} \right)y }={ 0.}$$

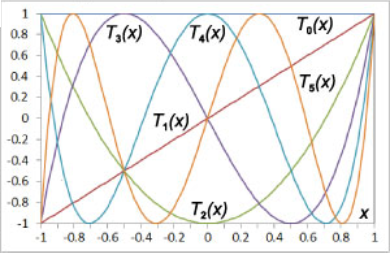
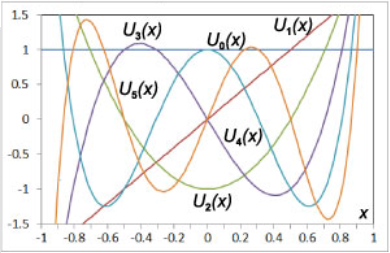
نمودار چندجمله‌ای‌های چبیشف نوع اول و دوم به‌ترتیب، در شکل‌های ۱ و ۲ نشان داده شده‌اند.

مثال ۱

جواب عمومی معادله دیفرانسیل زیر را برای $$\left| x \right| \lt 1$$ به‌دست آورید:

$$\left( {1 – {x^2}} \right)y^{\prime\prime} – xy’ + 2y= 0$$

حل: پارامتر معادله دیفرانسیل چبیشف، $$n = \sqrt 2$$ است. جواب عمومی را می‌توان به‌فرم مثلثاتی زیر نوشت:

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

$${y\left( x \right) }={ {C_1}\cos \left( {\sqrt 2 \arccos x} \right) }+{ {C_2}\sin\left( {\sqrt 2 \arccos x} \right)}$$

که در آن، $$C_1$$ و $$C_2$$ ثابت هستند. دقت کنید که در این حالت، به‌دلیل پارامتر $$\sqrt 2$$، جواب برحسب چندجمله‌های‌های چبیشف نیست.

مثال ۲

جواب عمومی معادله دیفرانسیل زیر را برای $$\left| x \right| \lt 1$$ به‌دست آورید:

$$\left( {1 – {x^2}} \right)y^{\prime\prime} – xy’ + 4y=0$$

حل: پارامتر معادله دیفرانسیل چبیشف، $$n = 2$$ است. بنابراین، می‌توان مستقیماً جواب عمومی را به‌شکل زیر نوشت:

$${y\left( x \right) }={ {C_1}\cos \left( {2\arccos x} \right) }+{ {C_2}\sin\left( {2\arccos x} \right)}$$

که در آن، $$C_1$$ و $$C_2$$ ثابت‌هایی اختیاری هستند.

جواب را می‌توان با چندجمله‌ای چبیشف نوع اول بیان کرد. از آن‌جایی که:

$${\cos \left( {2\arccos x} \right) = {T_2}\left( x \right) }={ 2{x^2} – 1}$$

جواب نهایی به‌صورت زیر خواهد بود:

$${y\left( x \right) }={ {C_1}\cos \left( {2\arccos x} \right) }+{ {C_2}\sqrt {1 – {\cos^2}\left( {2\arccos x} \right)} } \\
= {{C_1}{T_2}\left( x \right) + {C_2}\sqrt {1 – T_2^2\left( x \right)} } \\
= {{{C_1}\left( {2{x^2} – 1} \right) }+{ {C_2}\sqrt {1 – {{\left( {2{x^2} – 1} \right)}^2}} }} \\
= {{{C_1}\left( {2{x^2} – 1} \right) }+{ 2{C_2}x\sqrt {1 – {x^2}} .}}$$