جریان متغیر سریع در کانال باز – به زبان ساده

در مقاله جریان در کانال باز، جریان‌های غیریکنواخت یا متغیر را به دو دسته جریان متغیر تدریجی و جریان متغیر سریع تقسیم کردیم. در مقاله حاضر، جریان متغیر سریع را مورد بررسی قرار خواهیم داد که به اختصار $$\large \text {RVF}$$ نامیده می‌شود. اگر تغییرات عمق جریان در فاصله کوتاهی از مسیر جریان رخ دهد، جریان متغیر سریع خواهیم داشت. شماتیک نشان داده در شکل زیر را در نظر بگیرید. نمونه‌هایی از جریان متغیر سریع در دریچه‌های سد، سرریزهای تند و آبشارها تشکیل می‌شود. تغییر در سطح مقطع کانال، یکی از عوامل بروز جریان $$\large \text {RVF}$$ است.

تحلیل و بررسی جریان متغیر سریع

تحلیل جریان متغیر سریع به دلیل وجود اثرات چندبعدی و گذرا، جریان‌های برگشتی و همچنین جدایش جریان با پیچیدگی‌های زیادی همراه است. بنابراین، معمولاً این نوع جریان به صورت آزمایشگاهی و با روش‌های عددی بررسی می‌شود. ولی با وجود این پیچیدگی‌ها، برخی از انواع جریان را می‌توان با دقت خوبی به صورت جریان یک‌بعدی تحلیل کرد.

جریان در کانال‌هایی با شیب تند (Steep Slope) می‌تواند فوق‌بحرانی باشد. در ادامه به دلیل کاهش شیب کانال یا افزایش اثرات اصطکاکی، جریان قادر به حفظ حالت فوق‌بحرانی خود نیست و به زیر بحرانی تغییر می‌کند. هرگونه تغییر جریان از حالت فوق بحرانی به زیر بحرانی، از طریق یک پرش هیدرولیکی اتفاق می‌افتد. در پرش هیدرولیکی، آشفتگی و تلاطم بسیاری ایجاد شده و حجم زیادی از انرژی مکانیکی تلف می‌شود.

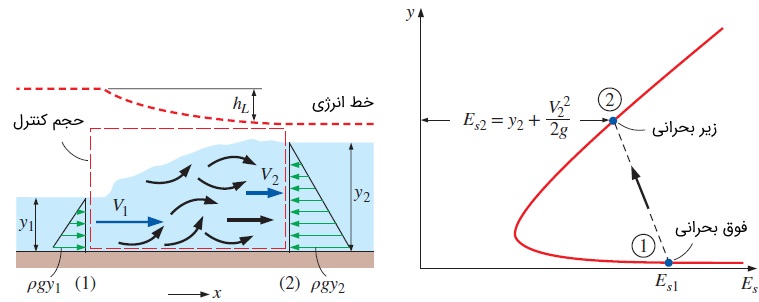
جریان پایدار عبوری از حجم کنترلی که اطراف پرش هیدرولیکی رسم شده را در نظر بگیرید. برای اینکه بتوانیم این پدیده را تحلیل کنیم، باید از فرض‌های زیر کمک بگیریم.

• سرعت در قسمت‌های ۱ و ۲ کانال تقریباً ثابت بوده و در نتیجه، ضرایب تصحیح شار-ممنتوم برابر $$\large \beta_1\:=\: \beta_2 \:\cong\:1$$ خواهند بود.
• فشار در مایع به صورت هیدرواستاتیکی تغییر می‌کند. از آنجایی که فشار اتمسفر به همه سطوح و در همه جهت‌ها وارد می‌شود و می‌توان آن را از طرفین ساده کرد، فقط از فشار نسبی استفاده می‌کنیم.
• تنش برشی دیواره و افت‌های مربوط به آن در مقایسه با افت‌های ناشی از شدت تلاطم در پرش هیدرولیکی، قابل صرف نظر کردن است.
• کانال، عریض است و در حالت افقی قرار دارد.
• هیچ‌گونه نیروی خارجی غیر از گرانش به حجم کنترل وارد نمی‌شود.

در کانالی با عرض $$\large b$$، رابطه پایستگی جرم ($$\large \dot {m} _1 \:=\: \dot {m} _2$$) به صورت عبارت‌های زیر بیان می‌شود.

$$\large \rho y_1 bV_1 \:=\: \rho y_2 bV_2 \\~\\ \large y_1 V_1 \:=\: y_2 V_2$$

(رابطه ۱)

تنها نیرویی که در جهت افقی و در راستای محور $$\large x$$ به حجم کنترل وارد می‌شود، نیروهای ناشی از فشار است. معادله ممنتوم را در جهت محور $$\large x$$ می‌نویسیم تا موازنه‌ای بین نیروهای ناشی از فشار هیدرواستاتیک و انتقال ممنتوم برقرار شود.

$$\large \sum _{} ^{} \overrightarrow{F} \:=\: \sum_ {out} ^{} \beta \dot{m} \overrightarrow{V} \:-\: \sum_ {in} ^{} \beta \dot{m} \overrightarrow{V} \\~\\ \large P_{1, \text {avg}} A_1 \:-\: P_{2, \text {avg}} A_2 \:=\: \dot{m} V_2 \:-\: \dot{m} V_1$$

در رابطه بالا، $$\large P_{1, \text {avg}}$$ و $$\large P_{2, \text {avg}}$$ به صورت زیر تعریف می‌شوند.

$$\large P_{1, \text {avg}} \:=\: \rho gy_1/2 \\~\\ \large P_{2, \text {avg}} \:=\: \rho gy_2/2$$

اگر عرض کانال برابر با $$\large b$$ باشد، روابط زیر نیز برقرار است.

$$\large A_1 \:=\: y_1b \\~\\ \large A_2 \:=\: y_2b \\~\\ \large \dot{m} \:=\: \dot{m}_2 \:=\: \dot{m}_2 \:=\: \rho A_1 V_1 \:=\: \rho y_1b V_1$$

با ادغام رابطه‌هایی که تا به اینجا نوشتیم، معادله ممنتوم برای این نوع جریان متغیر سریع به صورت زیر ساده می‌شود.

$$\large y_1^2 \:-\: y_2^2 \:=\: \frac {2y_1 V_1} {g} (V_2 \:-\: V_1)$$

(رابطه ۲)

با مقایسه رابطه‌های ۱ و ۲ می‌توانیم عبارت زیر را نتیجه بگیریم.

$$\large V_2 \:=\: (y_1/ y_2) V_1 \\~\\ \large \Rightarrow ~~~ y_1^2 \:-\: y_2^2 \:=\: \frac {2y_1 V_1^2} {gy_2} (y_1 \:-\: y_2) \\~\\ \large \Rightarrow ~~~ (\frac {y_2} {y_1})^2 \:+\: \frac {y_2} {y_1} \:-\: 2 \text {Fr} ^2_1 \:=\:0$$

در رابطه بالا، $$\large \text {Fr}$$ عدد فرود است و به صورت $$\large \text {Fr}_1 \:=\: V_1/ \sqrt {gy_1}$$ تعریف می‌شود. رابطه بالا، معادله‌ای درجه دوم برحسب متغیر $$\large y_2/ y_1$$ است و طبیعتاً دو ریشه (یکی منفی و دیگری مثبت) خواهد داشت. از آنجایی که هر دو پارامتر $$\large y_1$$ و $$\large y_2$$ مثبت هستند، پس مقدار $$\large y_2/ y_1$$ نمی‌تواند منفی باشد و جواب معادله درجه دوم بالا به شکل زیر است.

$$\large \frac {y_2} {y_1} \:=\: 0.5 (-1 \:+\: \sqrt {1 \:+\: 8 \text {Fr} _1^2})$$

(رابطه ۳)

از طرفی می‌دانیم که معادله انرژی برای این قسمت از جریان، برابر با رابطه زیر است.

$$\large y_1 \:+\: \frac {V_1^2} {2g} \:=\: y_2 \:+\: \frac {V_2^2} {2g} \:+\: h_L$$

با توجه به روابطی که در این مقاله ارائه شد، افت هد به صورت زیر نتیجه‌گیری می‌شود.

$$\large h_L \:=\: y_1 \:-\: y_2 \:+\: \frac {V_1^2 \:-\: V_2^2} {2g} \\~\\ \large \Rightarrow ~~~ h_L \:=\: y_1 \:-\: y_2 \:+\: \frac {y_1 \text {Fr}_1^2} {2} (1 \:-\: \frac {y_1^2} {y_2^2})$$

(رابطه ۴)

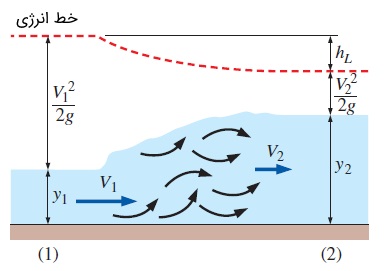
خط انرژی برای پرش هیدرولیکی در شکل قبل نشان داده شده است. قسمت نزولی این نمودار، نشان دهنده افت هد $$\large h_L$$ مربوط به پرش هیدرولیکی است. اگر مقادیر $$\large \text {Fr}_1$$ و $$\large y_1$$ مشخص باشد، عمق جریان پایین‌دست ($$\large y_2$$) و افت هد ($$\large h_L$$) را می‌توان با کمک رابطه‌های 3 و 4 محاسبه کرد. با رسم $$\large h_L$$ برحسب $$\large \text {Fr}$$ مشاهده می‌کنیم که در مقادیر $$\large \text {Fr} _1<1$$، افت هد $$\large h_L$$ منفی است. چنین چیزی غیرممکن است. زیرا در این حالت، آنتروپی منفی شده و قانون دوم نیوتن نقض خواهد شد. بنابراین، هنگامی که پرش هیدرولیکی رخ می‌دهد، جریان بالادست، فوق بحرانی ($$\large \text {Fr} _1>1$$) است. به عبارت دیگر، جریان زیر بحرانی هرگز به پرش هیدرولیکی ختم نمی‌شود. معادل این موضوع را می‌توان در جریان گازها نیز مشاهده کرد. در گازها، قبل از اینکه موج شوک رخ دهد، جریان به حالت فراصوت (عدد ماخ بزرگتر از یک) می‌رسد.

افت هد معیاری برای سنجش اتلاف انرژی مکانیکی به دلیل اصطکاک درونی سیال، فراهم می‌کند و همیشه قسمتی از انرژی مکانیکی را نشان می‌دهد که تلف می‌شود. اما در سوی دیگر، مواردی هم وجود دارد که هدف طراحی برخی از سازه‌ها، وقوع پرش هیدرولیکی است. در نتیجه، بخش زیادی از انرژی مکانیکی آب تلف شده و انرژی پتانسیل آن کاهش می‌یابد تا خسارات احتمالی به حداقل برسد. نمونه‌هایی از این نوع طراحی، حوضچه‌های آرامش (Stilling Basins) و سرریزهای سد (Spillways of dam) هستند. بدین منظور، ابتدا با تبدیل فشار بالا به سرعت خطیِ بالا، جریان فوق بحرانی تشکیل می‌شود. سپس با ایجاد تلاطم در جریان، بخشی از انرژی جنبشی تلف می‌شود. در نتیجه، برای سنجش عملکرد این جریان متغیر سریع باید نسبت انرژی تلف شده را بررسی کرد.

انرژی مخصوص سیال، پیش از پرش هیدرولیکی برابر $$\large E_{s1} \:=\: y_1 \:+\: V_1^2 /2g$$ است. از این رو، نسبت انرژی تلف شده به صورت زیر تعریف می‌شود.

$$\large \frac {h_L} {E_{s1}} \:=\: \frac {h_L} {y_1 \:+\: V_1^2 /2g} \:=\: \frac {h_L} {y_1 (1 \:+\: \text {Fr} _1^2 /2)}$$

اگر پرش هیدرولیکی ضعیف باشد ($$\large \text {Fr} _1<2$$)، نسبت انرژی تلف شده، در حدود چند درصد خواهد بود. همچنین در پرش‌های هیدرولیکی قوی ($$\large \text {Fr} _1>9$$)، این نسبت به $$\large 85$$ درصد نیز خواهد رسید. برخلاف شوک قائم در جریان گازها، که در مقطع عرضی رخ می‌دهد و می‌توان از ضخامت آن صرف نظر کرد، پرش هیدرولیکی در فاصله‌ای اتفاق می‌افتد که طول آن اندک نیست.

مثال: پرش هیدرولیکی در جریان متغیر سریع

سؤال: پس از یک دریچه سد، آب وارد یک کانال افقی شده و پرش هیدرولیکی در آن اتفاق می‌افتد. مقطع کانال، مستطیلی بوده و عرض آن برابر $$\large 10\:m$$ است. عمق جریان و سرعت آن، پیش از پرش، به ترتیب $$\large 0.8\:m$$ و $$\large 7\:m/s$$ اندازه‌گیری شده است. موارد زیر را تعیین کنید.

فیلم آموزش هیدرولیک پیشرفته (رایگان) در فرادرس

کلیک کنید

الف) عمق جریان و عدد فرود پس از پرش هیدرولیکی

ب) افت هد و نسبت انرژی تلف شده.

پ) توان بالقوه‌ای که به دلیل پرش هیدرولیکی هدر رفته است.

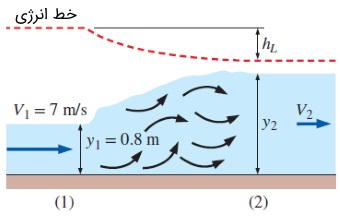
پاسخ: جریان را پایدار فرض می‌کنیم. الف) عدد فرود قبل از پرش به صورت زیر محاسبه می‌شود.

$$\large \text{Fr}_1 \:=\: \frac {V_1} {\sqrt {gy_1}} \:=\: \frac {7\: m/s} {\sqrt {(9.81\: m/s^2) (0.8 \:m)}} \:=\:2.50$$

عدد فرود از یک بزرگتر است. به همین دلیل، جریان قبل از پرش در حالت فوق بحرانی قرار دارد. عمق جریان، سرعت و عدد فرود پس از پرش هیدرولیکی به ترتیب زیر به دست می‌آید.

$$\large y_2 \:=\: 0.5y_1 (-1 \:+\: \sqrt {1\:+\: 8\text {Fr}_1 ^2}) \:=\: 0.5 (0.8\:m) (-1 \:+\: \sqrt {1\:+\: 8\times 2.50 ^2}) \\~\\ \large \Rightarrow ~~~ y_2 \:=\: 2.46\:m \\~\\ \large V_2\:=\: \frac {y_1} {y_2} V_1 \:=\: \frac {0.8\:m} {2.46\:m} (7\: m/s) \:=\: 2.28 \:m/s \\~\\ \large \text {Fr} _2\:=\: \frac {V_2} {\sqrt{gy_2}} \:=\: \frac {2.28\: m/s} {\sqrt {(9.81\: m/s^2) (2.46 \:m)}} \:=\:0.464$$

همان‌طور که می‌بینید، عمق جریان سه برابر شده و عدد فرود، به یک‌پنجم مقدار اولیه‌اش کاهش پیدا کرده است.

ب) برای تعیین افت هد در جریان متغیر سریع از معادله انرژی استفاده می‌کنیم.

$$\large h_L \:=\: y_1 \:-\: y_2 \:+\: \frac {V_1^2 \:-\: V_2^2} {2g} \\~\\ \large h_L \:=\: (0.8 \:m) \:-\: (2.46 \:m) \:+\: \frac {(7\: m/s)^2 \:-\: (2.28\: m/s)^2} {2(9.81\: m/s^2)} \\~\\ \large \Rightarrow ~~~ h_L \:=\: 0.572 \:m$$

اکنون، با کمک انرژی مخصوص آب، پیش از پرش هیدرولیکی، نسبت انرژی تلف شده محاسبه می‌کنیم.

$$\large E_{s1} \:=\: y_1 \:+\: \frac {V_1^2} {2g} \:=\: (0.8\:m) \:+\: \frac {(7\:m/s)^2} {2(9.81\: m/s^2)} \:=\: 3.30 \:m \\~\\ \large \frac {h_L} {E_{s1}} \:=\: \frac {0.572 \:m} {3.30 \:m} \:=\: 0.173$$

در واقع، $$\large 17.3$$ درصد از هد موجود (یا انرژی مکانیکی) تلف شده است (به انرژی گرمایی تبدیل شده است). دلیل این اتفاق هم چیزی جز اثرات اصطکاکی در حین پرش هیدرولیکی نیست.

پ) نرخ دبی جرمی آب به صورت زیر است.

$$\large \dot{m} \:=\: \rho \dot{V} \:=\: \rho by_1 V_1 \:=\: (1000\: kg/m^3) (0.8\:m) (10 \:m) (7\: m/s) \\~\\ \large \Rightarrow ~~~ \dot{m} \:=\: 56,000\: kg/s$$

اکنون می‌توانیم انرژی تلف شده ناشی از یک افت هد به میزان $$\large 0.572\:m$$ را تعیین کنیم.

$$\large \dot{E} _{dissipated} \:=\: \dot{m} gh_L \:=\: (56,000\: kg/s) (9.81\: m/s^2) (0.572 \:m) (\frac {1\:N} {1\:kg.m/s^2}) \\~\\ \large \Rightarrow ~~~ \dot{E} _{dissipated} \:=\: 314,000\: N.m/s \:=\: 314\:kW$$

نتیجه بالا نشان می‌دهد که در خلال جریان متغیر سریع نشان داده شده در این مثال، انرژی زیادی تلف می‌شود. در واقع، اگر به جای اینکه آب، روانه دریچه سد شود، آن را به سمت یک توربین هیدرولیکی هدایت کنیم، امکان تولید توان $$\large 314\:kW$$ وجود دارد. ولی این انرژی فقط صرف انرژی گرمایی شده که به صورت بی‌مصرف، وارد آب می‌شود. اختلاف دمایی که به دلیل این مقدار انرژی در آب رخ می‌دهد، به صورت زیر قابل محاسبه است.

$$\large \Delta T\:=\: \frac {\dot {E}} {\dot {m} c_p} \:=\: \frac {314 \:kJ/s} {(56,000 \:kg/s) (4.18\: kJ/kg .^\circ C)} \:=\: 0.0013 ^\circ C$$

توجه کنید که براساس اصل پایستگی انرژی، اگر برای این دبی آب از یک بخاری برقی با توان $$\large 314\:kW$$ استفاده شود، افزایش دمای آب، دقیقاً همین مقدار خواهد بود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
• جریان یکنواخت در کانال باز – به زبان ساده
• ورتکس (Vortex) چیست؟ — به زبان ساده
• جریان تراکم‌ پذیر (Compressible Flow) — اصول و مفاهیم

^^