جریان در کانال باز – از صفر تا صد

در مطالعه جریان در کانال باز همواره با مجرایی سر و کار داریم که سیال عبوری از آن، مایع است و سطح آزاد مایع، در معرض فشار اتمسفر قرار میگیرد. جریان در لوله، به دو دلیل گرانش یا اختلاف فشار برقرار میشود. ولی در کانالهای باز، سیال در حالت طبیعی و فقط به خاطر وجود گرانش، جاری میشود. مثلاً جریان رودخانه به دلیل اختلاف ارتفاع جریان در بالادست و پاییندست رخ میدهد. دبی جریان در کانال باز با استفاده از تعادل دینامیکی بین گرانش و اصطکاک قابل محاسبه است. در کاربردهای واقعی، مایع عبوری از کانال، معمولاً آب و جریان آن نیز متلاطم است. زیرا ویسکوزیته جنبشی، با اندازه کوچک و در مقیاس بزرگ وجود دارد. جریان، سهبعدی و در گاهی اوقات، ناپایدار است و به دلیل اثرات هندسی، پیچیدگیهایی دارد. در این مقاله، قاعدههای اساسی جریان در کانال باز و ارتباط آن با جریان یکبعدی پایدار در کانالهایی با سطح مقطعهای متداول را مورد بررسی قرار خواهیم داد.
انواع جریان در کانال باز
به جریان مایع در کانالهایی که در معرض اتمسفر هستند، جریان در کانال باز گفته میشود و با کمک سطح تماس گاز-مایع که سطح آزاد نام دارد، مشخص میشود. جریان آب در نهرها، رودخانهها و سیلابها، سیستمهای زهکشی آب در خیابانها و ناودان به کار رفته در ساختمانها، مثالهایی از جریان در کانال باز هستند. سیستمهای کانال باز ساخته شده به دست انسان، شامل سیستمهای آبیاری، خطوط فاضلاب، خندقهای زهکشی و جویهای آب میشود؛ که طراحی این سیستمها یکی از زمینههای کاربردی مهم در مهندسی مکانیک به شمار میرود.
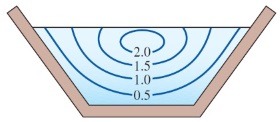
در یک کانال باز، سرعت جریان در سطوح کناری و پایین، صفر است. زیرا در این سطوح، لغزش وجود ندارد. در کانالهایی که هندسه متقارنی دارند، سرعت در صفحه میانی به بیشترین مقدار خود میرسد. مطابق شکل بالا، سرعت ماکسیمم در جایی پایینتر از سطح آزاد اتفاق میافتد. به دلیل اینکه جریانهای ثانویه، حتی در کانالهای مستقیم نیز وجود دارند، سرعت محوری، در نقطهای پایینتر از سطح آزاد، حدوداً در فاصله %$$\large 25$$ برابر عمق، به مقدار ماکسیمم میرسد. علاوه بر این، در بسیاری از موارد، سرعت سیال در جهت جریان نیز تغییر میکند. بنابراین، در حالت کلی، توزیع سرعت در کانالهای باز، سهبعدی است.
در کاربردهای مهندسی، معادلات برحسب سرعت متوسط در سطح مقطع کانال نوشته میشود. از آنجایی که سرعت متوسط فقط با فاصله طولی جریان ($$\large x$$) تغییر میکند، $$\large V$$ یک متغیر تکبعدی است. همین تکبعدی بودن جریان، به حل مسألههای واقعی با رویکردی ساده کمک میکند. برخلاف اینکه جریان تکبعدی ساده به نظر میرسد، در عمل، نتایج دقیقی را به همراه دارد.
جریان در کانال باز را میتوان به دو نوع پایدار (Steady) و غیر پایدار (Unsteady) دستهبندی کرد. در جریان پایدار، در یک نقطه مشخص، با گذشت زمان تغییری اتفاق نمیافتد. کمیت مورد نظری که تغییر آن بدین منظور بررسی میشود، ممکن است عمق جریان یا سرعت متوسط باشد. به عنوان مثال، اگر در هیچ نقطهای از کانال، عمق جریان با گذشت زمان تغییر نکند، جریان پایدار خواهد بود. در غیر این صورت، با یک جریان غیر پایدار مواجه هستیم.

انواع جریان در کانال باز -- یکنواخت و متغیر
همچنین میتوان جریان در کانال باز را با توجه به چگونگی تغییرات عمق جریان $$\large y$$ در طول کانال، به دو نوع یکنواخت و غیر یکنواخت (متغیر) تقسیم کرد. عمق جریان را میتوان با یکی از روشهای اندازهگیری سطح تعیین کرد. اگر عمق جریان (و در نتیجه، سرعت متوسط آن) در یک کانال ثابت بماند، جریان یکنواخت (Uniform) خواهد بود. در غیر این حالت، عمق جریان و سرعت متوسط در طول کانال، متغیر است. در این وضعیت، جریان از نوع غیر یکنواخت (Nonuniform) یا متغیر (Varied) خواهد بود. در قسمتهای مستقیم و طولانی کانالها که شیب، زبری (یا سختی) سطح و مساحت مقطع ثابت است، با جریان یکنواخت مواجه هستیم.
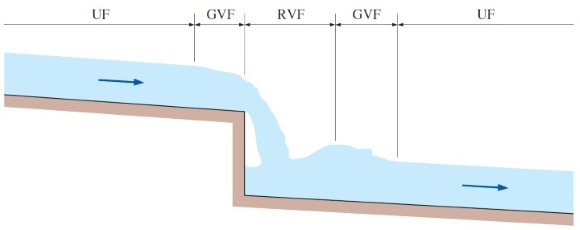
اگر در کانالهای باز، شیب و سطح مقطع ثابت بماند، سیال جاری در کانال، آنقدر شتاب میگیرد تا افت هد ناشی از اثرات اصطکاک با کاهش ارتفاع برابر شود. در این حالت، جریان یکنواخت است. عمق جریان در جریان یکنواخت، عمق قائم $$\large y_n$$ نام دارد و یکی از پارامترهای اصلی و مهم جریان در کانال باز محسوب میشود. وجود یک مانع در کانال، مانند یک دریچه، تغییر در شیب یا تغییر سطح مقطع، موجب تغییر در عمق جریان میشود. به چنین جریانی، جریان متغیر میگوییم. این جریان در هر دو نوع کانالهای باز طبیعی و مصنوعی (ساخته شده به دست انسان)، قابل مشاهده است. اگر در فاصله طولی کوتاهی در مسیر جریان، عمق جریان به میزان زیادی تغییر کند، جریان متغیر از نوع جریان متغیر سریع (Rapid Varied Flow) است. چنین جریانی را به اختصار با RVF نشان میدهیم. این اتفاق هنگام عبور جریان از دریچه نیمه باز یا آبشار مشهود است. اما اگر تغییر عمق جریان، آرام آرام و در مسافتی طولانی اتفاق بیافتد، جریان متغیر از نوع جریان متغیر تدریجی (Gradually Varied Flow) خواهد بود. جریان متغیر تدریجی را با GVF نمایش میدهیم. جریان GVF در فاصله بین جریان یکنواخت و جریان متغیر سریع رخ میدهد. به شکل بالا توجه کنید.
انواع جریان در کانال باز -- لایهای و متلاطم
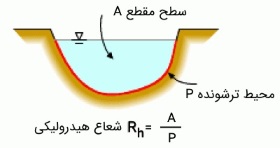
همانند جریان داخل لوله، جریان در کانال باز هم میتواند لایهای (Laminar)، انتقالی (Transitional) یا متلاطم (Turbulent) باشد. این جریانها براساس عدد رینولدز ($$\large Re \: = \: \frac { \:4 \: \rho \: V \: R_h \: } { \: \mu \: } \: = \: \frac { \: 4 \: V \: R_h \: } { \: \nu \: }$$) تعیین میشوند. در این رابطه $$\large V$$ سرعت متوسط مایع، $$\large \nu$$ ویسکوزیته سینماتیکی و $$\large R_h$$ هم شعاع هیدرولیکی (شکل زیر) است که به صورت نسبت سطح مقطع جریان به محیط تر شونده و به شکل زیر تعریف میشود.
$$\large R_h \: = \: \frac { \: A_c \: } { \: p \:}$$
همانطور که میدانید، قطر هیدرولیکی $$\large D_h$$ برای لوله به صورت $$\large D_h \: = \: \frac {4 \: A_c} {p}$$ تعریف میشود. در نتیجه، برای لوله دایرهای، قطر هیدرولیکی برابر با قطر لوله است. به طور کلی، قطر هیدرولیکی را میتوان برحسب شعاع هیدرولیکی نیز تعریف کرد.
$$\large D_h \: = \: \frac {4 \: A_c} {p} \: = \: 4 \: R_h$$
جریان لایهای هنگامی تشکیل میشود که یک لایه نازک از آب (مانند زهکشی آب باران در یک خیابان) با سرعت بسیار کمی جاری شود. ویسکوزیته سینماتیکی آب در دمای $$\large 20 \: ^ \circ C$$ برابر با $$\large 1.0 \: \times \: 10 ^{-6} \: ^ \circ C$$ و سرعت متوسط آن در کانالهای باز معمولاً برابر $$\large 0.5 \: m / s$$ است. از طرفی هم شعاع هیدرولیکی عموماً بیشتر از $$\large 0.1 \: m$$ است. در نتیجه، عدد رینولدز برای آب در جریان در کانال باز بیشتر از $$\large 200,000$$ خواهد بود. از همین رو، نوع جریان، در بیشتر مواقع، متلاطم است. توجه کنید که محیط تر شونده، شامل بخشهایی از دیوارهها و کف کانال میشود که با سیال جاری در تماس است. به عنوان مثال، محیط تر شونده و سطح مقطع جریان در یک کانال مستطیلی (مطابق شکل زیر) به ارتفاع $$\large h$$ و عرض $$\large b$$ که تا عمق $$\large y$$ پر از آب است، به ترتیب برابر با $$\large p \: = \: b \: + \: 2 \:y$$ و $$\large A_c \: = \: y b$$ محاسبه میشود. شعاع هیدرولیکی برای این کانال مطابق رابطه زیر به دست میآید.
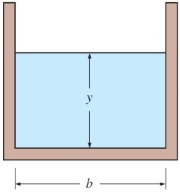
$$\large R_h \: = \: \frac {A_c} {p} = \frac {y b} {b \: + \: 2 y} \: = \: \frac {y} {1 \: + \: 2 y / b}$$
به عنوان مثالی دیگر، جریان یک فیلم مایع را روی سطحی بزرگ در نظر بگیرید. فیلم مایع را در شکل زیر مشاهده میکنید. از آنجایی که $$\large b \: \gg \: y$$، مطابق رابطه زیر، شعاع هیدرولیکی برابر با ضخامت لایه سیال است.
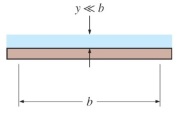
$$\large R_h \: = \: \frac {A_c} {p} = \frac {y b} {b \: + \: 2 y} \: \cong \: \frac {y b} {b} \: \cong \: y$$
در دو شکل زیر نیز، کانالهای ذوزنقهای و دایرهای را مشاهده میکنید که شعاع هیدرولیکی برای هر یک محاسبه شده است.
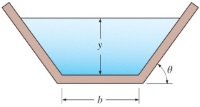
$$\large R_h \: = \: \frac {A_c} {p} \: = \: y \times \frac { b \: + \: \frac {y} {\tan \theta}} {b \: + \: \frac {2 y} {\sin \theta}}$$
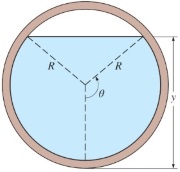
$$\large R_h \: = \: \frac {A_c} {p} \: = \: \frac { R ^ 2 \: (\theta \: - \: \sin \theta \: \cos \theta)} {2 R \: \theta} \: = \: R \: \times \: \frac {\theta \: - \: \sin \theta \: \cos \theta} {2 \: \theta}$$
عدد فرود و سرعت موج جریان در کانال باز
شیوه دیگر دستهبندی جریان در کانال باز با کمک عدد بیبُعد فرود (Froude Number) انجام میشود. براساس عدد فرود، میتوان جریان را به سه حالت زیر بحرانی (Subcritical)، بحرانی (Critical) و فوق بحرانی (Supercritical) تقسیم کرد. عدد فرود با کمک رابطه $$\large Fr \: = \: \frac {V} {\sqrt {g L_c}}$$ به دست میآید. در این رابطه، $$\large L_c$$ برابر با طول مشخصه است. طول مشخصه در کانالهای مستطیلی عریض، همان عمق جریان و برابر $$\large y$$ در نظر گرفته میشود. در حالتهایی که عدد فرود کوچکتر از یک، برابر یک و بزرگتر از یک باشد، به ترتیب با جریانهای زیر بحرانی، بحرانی و فوق بحرانی مواجه خواهیم بود.
این سه حالت، دقیقاً با عدد ماخ (Mach Number) در جریان تراکمپذیر، متناظر است. همچنین عدد فرود به صورت نسبت سرعت سیال به سرعت موج ($$\large Fr \: = \: \frac {V} {c_0}$$) هم تعریف میشود. از طرف دیگر، میتوان عدد فرود را به عنوان ریشه نسبت نیروی اینرسی (یا دینامیکی) به نیروی گرانشی (یا وزن) در نظر گرفت. برای نشان دادن این موضوع، مطابق رابطه زیر، صورت و مخرج کسر را در عبارت $$\large \rho \: A$$ ضرب کردهایم. عبارت سمت راست، با نسبت نیروی اینرسی به نیروی گرانشی متناسب است.
$$\large Fr ^ 2 \: = \: \frac {V ^ 2 \: \: \: \: \: \: \times \rho A} {g \: L_c \: \: \: \: \times \rho A} \: = \: \frac {2 (\frac {1} {2} \rho \: V^2 A)} {mg}$$
در نتیجه، هنگامی که عدد فرود بزرگ باشد، نیروهای اینرسی و هنگامی که عدد فرود کوچک باشد، نیروهای گرانشی غالب هستند. به عبارت دیگر، هنگامی که سرعت سیال پایین است ($$\large Fr \: < \: 1$$)، خبر یک اعوجاج کوچک، با سرعت $$\large c_0 \: - \: V$$ نسبت به ناظر ساکن، به بالادست منتقل میشود و روی شرایط بالادست اثر میگذارد. ولی هنگامی که سرعت سیال بالا باشد ($$\large Fr \: > \: 1$$)، خبر اعوجاجهای کوچک به بالادست منتقل نمیشود. در حقیقت، موج با سرعت $$\large V \: - \: c_0$$ نسبت به ناظر ساکن، به سمت پاییندست در حال حرکت است. در این حالت، اصطلاحاً موج به سمت پاییندست جارو میشود. بنابراین، شرایط بالادست جریان تغییر نمیکند. به عبارت دیگر، هنگامی که $$\large Fr \: < \: 1$$ باشد، موج به سمت بالادست حرکت میکند؛ هنگامی که $$\large Fr \: > \: 1$$ باشد، موج به طرف پاییندست منتشر میشود و زمانی که $$\large Fr \: = \: 1$$ برقرار باشد، موج روی سطح ساکن میماند. همچنین در نظر داشته باشید که سرعت انتشار موج در کانالهای عمیقتر در مقایسه با کانالهای کمعمق، بیشتر است.
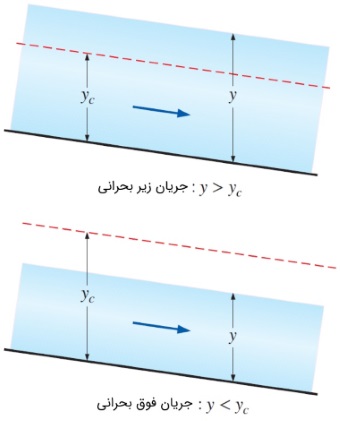
جریان سیال در یک کانال باز مستطیلی را مطابق شکل بالا در نظر بگیرید. سطح مقطع کانال و نرخ دبی حجمی را به ترتیب با $$\large A_c$$ و $$\large \dot{V}$$ نشان میدهیم. هنگامی که جریان در کانال باز بحرانی باشد، سرعت متوسط سیال برابر $$\large V \: = \: \sqrt{g \: y_c}$$ میشود. به $$\large y_c$$، عمق بحرانی گفته میشود. برای به دست آوردن عمق بحرانی در کانال مستطیلی، به ترتیب زیر عمل میکنیم.
$$\large \dot{V} \: = \: A_c \: V \: = \: A_c \: \sqrt{g \: y_c} \\~\\
\large \Rightarrow ~~~ y_c \: = \: \frac { \dot{ V } ^ 2 } { g \: A^2_c }$$
(رابطه ۱)
$$\large A_c \: = \: b \: y_c$$
(رابطه ۲)
با ادغام رابطههای ۱ و ۲، نتیجه زیر به دست میآید.
$$\large y_c \: = \: (\frac {\dot{V}^2} {g \: b ^ 2}) ^ {1/3}$$
همانطور که در شکل قبل نشان داده شد، عمق سیال در جریان زیر بحرانی و فوق بحرانی به ترتیب در نامساویهای $$\large y \: > \: y_c $$ و $$\large y \: < \: y_c $$ صدق میکند. همانند جریان تراکمپذیر، در اینجا هم سیال میتواند از حالت زیر بحرانی به جریان فوق بحرانی تبدیل شود. از سوی دیگر، این امکان وجود دارد که از شتاب جریان فوق بحرانی کاسته شده و به جریان زیر بحرانی تبدیل شود. چنین پدیدهای با بروز یک شوک اتفاق میافتد که پرش هیدرولیکی نام دارد.
سرعت امواج سطحی جریان در کانال باز
تشکیل موج روی سطح آزاد آب، پدیده آشنایی است که همه ما در دریا، رودخانه و حتی استخر آن را مشاهده کردهایم. دامنه این امواج، بسیار گسترده است. برخی از آنها به ارتفاع چندین متر میرسند و برخی دیگر به سختی دیده میشوند. برای درک بهتر برخی از جنبههای جریان در کانال باز، بهتر است خلاصهای از اساس حرکت موج را تشریح کنیم. یکی از پارامترهای اصلی در مطالعه جریان در کانال باز، سرعت موج است که آن را با $$\large c_0$$ نشان میدهیم. کانالی با عرض و طول زیاد را در نظر بگیرید که در ابتدا سیالی به ارتفاع $$\large y$$ و به حال سکون در آن قرار دارد. انتهای کانال، مطابق شکل زیر، با سرعت $$\large \delta V$$ شروع به حرکت میکند. در این حالت، موج سطحی با ارتفاع $$\large \delta y$$ و با سرعت $$\large c_0$$ به سمت مایع ساکن منتشر میشود.
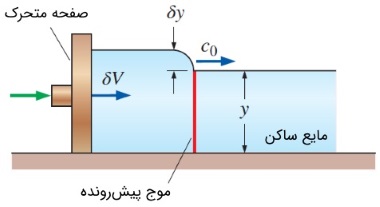
اکنون، حجم کنترلی را در نظر بگیرید که این موج را در برگرفته و همراه با آن حرکت میکند. همانگونه که در شکل زیر نشان داده شده است، از چشم ناظر سوار بر موج، قسمتی از سیال که در سمت راست حجم کنترل قرار دارد، با سرعت $$\large c_0$$ به سمت چپ حرکت میکند. از سوی دیگر، قسمتی از سیال که در سمت چپ موج قرار گرفته است، با سرعت $$\large c_0 \: - \: \delta V$$ حرکت میکند. در این حالت، از چشم ناظری که با موج حرکت میکند، این یک فرآیند جریان پایدار محسوب میشود. موازنه جرم ($$\large \dot{m}_1 \: = \: \dot{m}_2$$) برای حجم کنترل نشان داده شده در شکل را میتوان به صورت زیر نشان داد. عرض حجم کنترل برابر $$\large b$$ است.
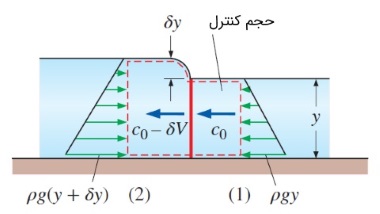
$$\large \rho c_0 y b \: = \: \rho ( c_0 \: - \: \delta V ) ( y \: + \: \delta y ) b \\~\\
\large \Rightarrow ~~~ \delta V \: = \: c_0 \: \frac {\delta y} {y \: + \: \delta y}$$
در ادامه، پنج فرض زیر را در نظر میگیریم:
- سرعت جریان در کانال باز تقریباً ثابت است. در نتیجه، ضرایب تصحیح شار ممنتوم (Momentum Flux) برابر واحد خواهد بود.
- از اصطکاک در سطح زیرین و نیروی درگ هوا در بالا، چشمپوشی میکنیم.
- اثرات دینامیکی ناچیز هستند. از این رو، فشار مایع به صورت هیدرواستاتیکی تغییر میکند. فشار نسبی در نقطه شماره ۱، $$\large P_{1, \: avg} \: = \: \rho g h_{1, \: avg} \: = \: \rho g (y/2)$$ و در نقطه شماره ۲، برابر $$\large P_{2, \: avg} \: = \: \rho g h_{2, \: avg} \: = \: \rho g (y \: + \: \delta y)/2$$ است.
- نرخ دبی جرمی، ثابت و برابر $$\large \dot{m}_1 \: = \: \dot{m}_2 \: = \: \rho c_0 y b$$ است.
- هیچ نیرویی از بیرون وارد نمیشود. بنابراین، تنها نیروهایی که در جهت محور $$\large x$$ به حجم کنترل وارد میشود، نیروهای حاصل از فشار است.
با این توضیحات، معادله ممنتوم $$\large \sum_{ } \overrightarrow{ F } \: = \: \sum_{ out } \beta \dot{ m } \overrightarrow{ V } \: - \: \sum_{ in } \beta \dot{ m } \overrightarrow{ V }$$ در جهت محور $$\large x$$ به موازنهای بین نیروهای حاصل از فشار هیدرواستاتیکی و انتقال ممنتوم بدل میشود.
$$\large P_{2, \: avg} \: \times \: A_2 \: - \: P_{1, \: avg} \: \times \: A_1 \: = \: \dot { m } \: (- \; V_2) \: - \: \dot { m } \: (- \; V_1)$$
توجه کنید که سرعتهای متوسط در ورودی و خروجی به حجم کنترل، در جهت محور منفی $$\large x$$ هستند و در نتیجه، مقدارشان منفی خواهد بود. اکنون رابطه قبلی به شکل زیر نوشته میشود.
$$\large \frac { \rho g (y \: + \: \delta y) ^2 b} {2} \: - \: \frac { \rho g y^2 b} {2} \: = \: \rho c_0 y b ( - \: c_0 \: + \: \delta V ) \: - \: \rho c_0 y b ( - \: c_0) \\~\\
\large \Rightarrow g ( 1 \: + \: \frac { \delta y } { 2 y } ) \delta y \: = \: c_0 \: \delta V$$
ادغام رابطههای ممنتوم و پایستگی و بازنویسی آن، نتیجه زیر را در پی خواهد داشت.
$$\large c^2_0 \: = \: g y ( 1 \: + \: \frac { \delta y } { 2 y } ) (1 \: + \: \frac { \delta y } { y } )$$
مطابق این رابطه، سرعت موج ($$\large c_0$$) با ارتفاع موج ($$\large \delta y$$) متناسب است. برای امواج سطحی بسیار کوچک، میتوانیم از فرض $$\large \delta y \: \ll \: y$$ استفاده کنیم تا سرعت موج برابر با رابطه $$\large c_0 \: = \: \sqrt { g \: y }$$ شود. اکنون میدانیم سرعت امواج سطحی بسیار کوچک، با ریشه دوم عمق مایع تناسب دارد. این موضوع را فراموش نکنید که این روابط فقط برای قسمتهای کمعمق مایع، مانند جریان در کانال باز معتبر است. در غیر این صورت و اگر عمق مایع زیاد باشد (مانند اقیانوس)، سرعت موج، مستقل از عمق مایع خواهد بود.
همچنین میتوان سرعت موج را به جای ادغام روابط ممنتوم و پایستگی جرم، با کمک موازنه انرژی محاسبه کرد. این نکته را نیز در نظر داشته باشید که امواج، در نهایت به دلیل وجود اثرات ویسکوز، متوقف میشوند؛ ولی در این مقاله از این اثرات چشمپوشی شده است. از سوی دیگر، در جریان در کانال باز با سطح مقطعی غیر از مستطیل، برای محاسبه عدد فرود، به جای عمق جریان ($$\large y$$) باید از عمق هیدرولیکی (Hydraulic Depth) استفاده کرد که به صورت $$\large y_h \: = \: \frac { A_c} { L_t }$$ تعریف میشود. در این رابطه، $$\large L_t$$ عرض بالایی در قطاع جریان است. به عنوان مثال، برای یک کانال دایرهای که نیمی از سطح آن از سیال پر شده باشد، عمق هیدرولیکی برابر رابطه $$\large y_h \: = \: \frac { \pi R^2 / 2} { 2 R} \: = \: \pi R / 4$$ به دست میآید.
احتمالاً این پدیده را مشاهده کردهاید که وقتی سنگی به داخل حوضچهای از آب پرتاب شود، امواجی هممرکز تشکیل میشود که در تمام جهات منتشر شده و پس از فاصلهای ناپدید میشوند. اما هنگامی که سنگی را به داخل رودخانه پرتاب کنیم، قسمت بالادست موج، با توجه به بحرانی بودن جریان، رفتار متفاوتی از خود نشان میدهد. اگر جریان سیال در شرایط زیر بحرانی ($$\large V \: < \: c_0$$) باشد، این قسمت به سمت بالادست حرکت میکند. اگر شرایط سیال، فوق بحرانی ($$\large V \: > \: c_0$$) باشد، قسمت بالادست جریان به سمت پاییندست حرکت میکند. اما اگر جریان سیال، بحرانی ($$\large V \: = \: c_0$$) باشد، در همان نقطه ساکن خواهد ماند.
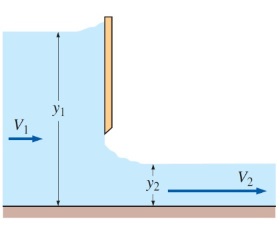
اهمیت زیر بحرانی یا فوق بحرانی بودن جریان را با مثالی نشان میدهیم. فرض کنید تکه سنگی در کف رودخانه افتاده باشد. در این حالت، زیر بحرانی یا فوق بحرانی بودن جریان تعیین میکند که سطح آب در آن نقطه بالا یا پایین برود. علاوه بر این، اگر جریان زیر بحرانی باشد، سطح آب در جهت جریان به صورت تدریجی کاهش مییابد. ولی اگر جریان از نوع فوق بحرانی باشد، جهشی ناگهانی در سطح آب رخ میدهد و جریان از حالت فوق بحرانی به حالت زیر بحرانی تغییر میکند. به این پدیده، پرش هیدرولیکی (Hydraulic Jump) گفته میشود که قبلاً در مجله فرادرس به طور مفصل به آن پرداخته شده است.
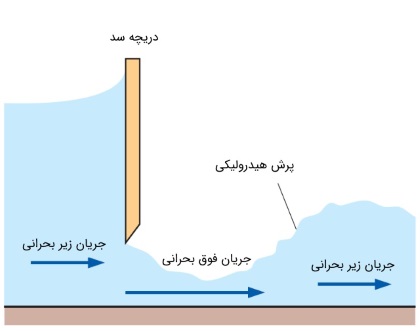
تصویر شماتیک پرش هیدرولیکی را در شکل بالا مشاهده میکنید. آب با سرعت زیر بحرانی به دریچه سد میرسد. سطح آب در بالادست به قدری زیاد است که بتواند آبِ در حال عبور از دریچه را به سطح فوق بحرانی برساند (مانند اتفاقی که برای گازها در نازل همگرا--واگرا میافتد). حال به دلیل اینکه قسمت پاییندست کانال به اندازه کافی شیبدار نیست، آب قادر به حفظ سرعت فوق بحرانیِ خود نیست و به ارتفاع بالاتری میرود که سطح مقطع بزرگتری داشته باشد. بدین ترتیب، سرعت آب به حالت زیر بحرانی برمیگردد.
انرژی مخصوص جریان در کانال باز
جریان سیال در یک کانال باز را در نظر بگیرید. عمق جریان و سرعت متوسط آن به ترتیب برابر $$\large y$$ و $$\large V$$ است. همچنین ارتفاع کف کانال را نسبت به یک مرجع بیرونی با $$\large z$$ دادهایم. شکل زیر را مشاهده کنید.
برای سادگی فرض میکنیم سرعت سیال در همه نقاط مقطع کانال برابر $$\large V$$ باشد. انرژی مکانیکی کل سیال در این کانال، برحسب هد به صورت زیر قابل تعریف است.
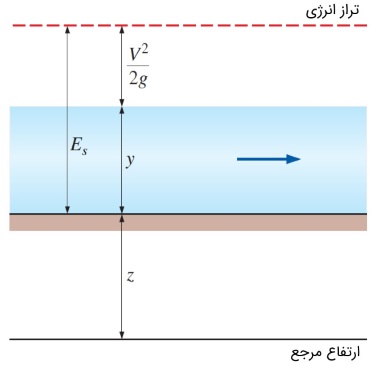
$$\large H \: = \: z \: + \: \frac {P} {\rho g} \: + \: \frac {V ^ 2} {2 g } \: = \: z \: + \: y \: + \: \frac { V ^ 2} {2 g }$$
پارامتر $$\large z$$، هد ارتفاع و $$\large y$$ هد فشار نسبی را نشان میدهد. هد سرعت یا هد دینامیکی هم با $$\large \frac { V ^2} {2 g }$$ تعریف شده است. انرژی کل بیان شده در رابطه بالا، نمیتواند ارائه درستی از انرژی سیال جاری باشد؛ زیرا مقدار هد ارتفاع و مرجع اندازهگیری آن دلخواه است. اگر هد ارتفاع نسبت به کف کانال محاسبه شود، مقدار $$\large z$$ برابر صفر خواهد بود و انرژی مکانیکی کل برای این سیال، مساوی با مجموع هدهای دینامیکی و فشار خواهد بود. مجموع هد فشار و هد دینامیکی جریان در کانال باز را با نماد $$\large E_s$$ نشان میدهیم و آن را انرژی مخصوص مینامیم. بنابراین، انرژی مخصوص به صورت زیر تعریف میشود.
$$\large E_s \: = \: y \: + \: \frac { V ^ 2} {2 g }$$
حال، فرض کنید سطح مقطع این کانال به شکل مستطیل و عرض آن برابر $$\large b$$ باشد. همانطور که میدانیم، نرخ دبی حجمی این جریان در کانال باز با کمک رابطه $$\large \dot {V} \: = \: A_c \:V \: = \: y \: b \: V$$ به دست میآید. از این رو، انرژی مخصوص را میتوانیم برای آن بازنویسی کنیم.
$$\large E_s \: = \: y \: + \: \frac { \dot{V} ^ 2} {2 \: g \: b^2 y^2 }$$
در رابطه بالا، تفاوت انرژی مخصوص با عمق جریان، مشهود است. در حین جریان پایدار سیال در یک کانال باز، نرخ دبی ثابت میماند. شکل زیر نمودار انرژی مخصوص را برحسب $$\large y$$ نشان میدهد. با توجه به این نمودار که در آن، $$\large \dot {V}$$ و $$\large b$$ ثابت هستند، میتوان موارد زیر را نتیجهگیری کرد:
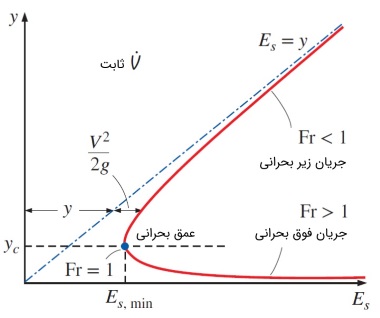
- فاصله هر نقطه روی محور عمودی $$\large y$$ تا منحنی، انرژی مخصوص آن نقطه را نشان میدهد. ناحیه بین خط $$\large E_s \: = \: y$$ منحنی، بیانکننده هد دینامیکی (یا هد انرژی جنبشی) مایع بوده و سایر نواحی مربوط به هد فشار (یا هد انرژی پتانسیل) است.
- هرچه $$\large y \: \rightarrow \: 0$$، انرژی مخصوص نیز به سمت بینهایت میل میکند. زیرا در این محدوده، سرعت به سمت بینهایت میرود. از سوی دیگر، هنگامی که عمق جریان ($$\large y$$) زیاد میشود، انرژی مخصوص با عمق جریان برابر است. زیرا در این ناحیه، سرعت و انرژی جنبشی بسیار کوچک خواهد بود. مقدار انرژی مخصوص در نقطهای بین این دو ناحیه، به کمترین میزان خود، یعنی $$\large E_{s, \: min}$$، میرسد. این نقطه را نقطه بحرانی (Critical Point) مینامیم. عمق بحرانی $$\large y_s$$ و سرعت بحرانی $$\large V_s$$، مشخصههای این نقطه هستند. مقدار انرژی در این نقطه به انرژی بحرانی نیز معروف است.
- هر خط افقی، منحنی انرژی مخصوص را فقط در یک نقطه قطع میکند. در نتیجه، بین عمق جریان در کانال باز و انرژی مخصوص، تناظر یک به یک برقرار است. از طرفی، اگر $$\large E_s \: > \: E_{s, \: min}$$، هر خط عمودی، منحنی را در دو نقطه قطع میکند. یعنی هر مقدار انرژی مخصوص میتواند با دو عمق جریان مختلف متناظر باشد. این دو عمق، عمقهای جایگزین نامیده میشوند. به عنوان مثال، در جریان عبوری از دریچه یک سد و با فرض افت اصطکاک ناچیز (یعنی در شرایطی که انرژی مخصوص ثابت بماند)، عمق بیشتر و کمتر، مطابق شکل زیر، به ترتیب با بالادست و پاییندست جریان متناظر هستند.
- تغییر کوچک انرژی مخصوص در نزدیکی نقطه بحرانی، تفاوت بین عمقهای جایگزین را به شدت زیاد میکنند. همین امر، موجب نوسان شدید در سطح آب خواهد شد. بنابراین، در طراحی کانالهای روباز، باید حتیالامکان از این ناحیه فاصله گرفت.
حداقل مقدار انرژی مخصوص و عمق بحرانی را میتوان با مشتقگیری از رابطهای که برای انرژی مخصوص تعریف کردیم، به دست آورد. با ثابت فرض کردن $$\large \dot {V }$$ و $$\large b$$، مشتقگیری نسبت به $$\large y$$ و قرار دادن آن برابر صفر، عمق بحرانی به شیوه زیر محاسبه میشود.
$$\large \frac {d E_s} {d y} \: = \: \frac {d} {d y} (y \: + \: \frac {\dot {V} ^2} {2 g b ^2 y ^2}) \: = \: 1 \: - \: \frac {\dot{V} ^2} {g b ^2 y^3} \: = \: 0 \\~\\
\large \Rightarrow ~~~ y_c \: = \: (\frac {\dot {V} ^2} {g b^2} ) ^ {1/3}$$
در این نقطه، سرعت جریان با سرعت موج برابر بوده و در نتیجه، عدد فرود برابر یک خواهد بود. میتوان این گونه نتیجه گرفت که وقتی انرژی مخصوص به کمترین مقدار خود برسد، جریان به حالت بحرانی در خواهد آمد. اکنون با علم به اینکه سرعت در نقطه بحرانی برابر $$\large V_c \; = \: \sqrt {g \: y_c}$$ است، حداقل انرژی مخصوص را میتوان با رابطه زیر نشان داد.
$$\large E_{s, \: min} \: = \: y_c \: + \: \frac {V^2_c} {2 g} \: = \: y_c \: + \: \frac {g \:y_c} {2 g} \: = \: \frac {3} {2} y_c$$
در جریان یکنواخت، عمق جریان، سرعت جریان و انرژی مخصوص ثابت میمانند؛ زیرا رابطه $$\large E_s \: = \: y \: + \: \frac {V^2} {2 g}$$ برقرار است. افت هد را میتوان با کاهش ارتفاع (از طریق شیبدار کردن کف کانال) جبران کرد. در جریان غیریکنواخت، انرژی مخصوص با توجه به شیب کانال و افتهای اصطکاکی، ممکن است کاهش یا افزایش یابد. اگر کاهش ارتفاع در قسمتی از جریان، بیشتر از افت هد در آن قسمت باشد، انرژی مخصوص به میزان اختلاف بین این دو هد، بیشتر خواهد شد.
مثال
سؤال: آب به صورت پایدار و با دبی $$\large 0.2 \: m^3 /s$$ در کانالی در جریان است. سطح مقطع کانال مستطیلی بوده و عرض آن برابر $$\large 0.4 \: m$$ است. شماتیک این جریان در کانال باز را در شکل زیر مشاهده میکنید. اگر عمق جریان $$\large 0.15 \: m$$ باشد، سرعت جریان و زیر بحرانی یا فوق بحرانی بودن آن را مشخص کنید. حال اگر حالت جریان تغییر کند، عمق جایگزین جریان را بیابید.
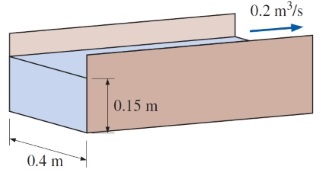
پاسخ: ابتدا سرعت متوسط جریان در کانال باز را به صورت زیر محاسبه میکنیم.
$$\large V \: = \: \frac {\dot { V}} {A_c } \: = \: \frac {\dot { V}} {y \: b } \: = \: \frac { 0.2 \: m^3 /s} {(0.15 \: m) \: (0.4 \: m)} \: = \: 3.33 \: m/s$$
اکنون، برای پیدا کردن عمق بحرانی به شیوه زیر عمل میکنیم.
$$\large y_c \: = \: (\frac {\dot{V} ^ 2} {g \: b^ 2}) ^ {1/3} \: = \: (\frac {(0.2 \: m^3 /s) ^2} {( 9.81 \: m /s ^2 ) \: ( 0.4 \: m) ^2}) ^ {1 /3} \: = \: 0.294 \: m$$
از آنجایی که عمق جریان در حالت طبیعی برابر $$\large y \: = \: 0.15 \: m$$ است و $$\large y \: < \: y_c$$، میتوان نتیجه گرفت که جریان در حالت فوق بحرانی قرار دارد. راه دیگر برای تعیین وضعیت جریان، محاسبه عدد فرود است.
$$\large Fr \: = \: \frac {V} {\sqrt {g \: y} } \: = \: \frac {3.33 \: m/s} {\sqrt { (9.81 \: m/s^2) (0.15 \: m)} } \: = \: 2.75$$
همانطور که میبینیم عدد فرود بیشتر از یک است. در نتیجه، با جریان فوق بحرانی مواجه هستیم. در این حالت، انرژی مخصوص به شیوه زیر قابل محاسبه است.
$$\large E_ {s 1} \: = \: y_1 \: + \: \frac {\dot {V} ^2} {2 g \: b ^2 y^2_1} \: = \: (0.15 \: m) \: + \: \frac {(0.2 \: m^3 / s ) ^2} {2 \: (9.81 \: m/ s ^2) \: (0.4 \: m) ^2 (0.15 \: m) ^2} \: = \: 0.7163 \: m$$
اکنون با کمک رابطه $$\large E_ {s 1} \: = \: E_ {s 2}$$، عمق جایگزین را به دست میآوریم.
$$\large E_ {s 2} \: = \: y_2 \: + \: \frac {\dot{V} ^2} {2 g \: b^2 y^2_2} \\~\\
\large \Rightarrow ~~~ 0.7163 \: m \: = \: y_2 \: + \: \frac {(0.2 \: m ^3 /s) ^2 } {2 \: (9.81 \: m/ s^2) \: (0.4 \: m) ^2 \: y^2 _2} \\~\\
\large \Rightarrow ~~~ y_2 \: = \: 0.69 \: m$$
بنابراین، در انتقال جریان از حالت فوق بحرانی تا زیر بحرانی، عمق جریان در کانال باز از $$\large 0.15 \: m$$ تا $$\large 0.69 \: m$$ تغییر میکند.
پایستگی جرم و انرژی جریان در کانال باز
چگالی جریان در کانال باز تقریباً ثابت است. از این رو، معادله پایستگی جرم برای حالت یکبعدی و پایدار جریان در کانال باز را میتوان به صورت زیر نوشت. بنا به این رابطه، حاصلضرب سطح مقطع در سرعت متوسط جریان ثابت است.
$$\large \dot {V} \: = \: A_c \: \times \: V$$
از رابطه بالا میتوانیم برای نوشتن پیوستگی جریان بین دو نقطه به صورت $$\large A_{c1} \: \times \: V_1 \: = \: A_{c2} \: \times \: V_2 \:$$ استفاده کنیم. این معادله، مشابه معادله پیوستگی جریان در لوله است. توجه کنید که سطح مقطع و سرعت متوسط جریان ممکن است در طول مسیر تغییر کنند ولی حاصلضرب آنها ثابت باقی میماند. برای تعیین انرژی کل جریان در کانال باز شکل زیر را در نظر بگیرید. نقطه $$\large A$$ در مایع، در فاصلهای برابر با $$\large a$$ از سطح آزاد قرار دارد. ارتفاع نقطه $$\large A$$ و سرعت جریان در آن به ترتیب برابر $$\large z_A \: = \: z \: + \: ( y \: - \: a)$$ و $$\large V_A \: = \: V$$ است. فشار هیدرواستاتیک در این نقطه را نسبت به سطح آزاد با $$\large P_A \: = \: \rho \: g \: a$$ نشان دادهایم. در نتیجه، انرژی کل مایع برحسب هد به صورت زیر تعریف میشود.
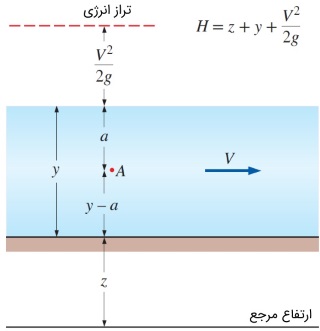
$$\large H_A \: = \: z_A \: + \: \frac {P_A} {\rho g} \: + \: \frac {V^2 _ A } {2 g} \: = \: z \: + (y \: - \: a) \: + \: \frac {\rho g a} {\rho g} \: + \: \frac {V ^2} {2 g} \\~\\
\large \Rightarrow ~~~ H_A \: = \: z \: + \: y \: + \: \frac {V ^2} {2 g}$$
همانطور که ملاحظه میکنید، رابطه به دست آمده، مستقل از مکان نقطه $$\large A$$ در سطح مقطع جریان است. به این ترتیب میتوانیم معادله انرژی را بین بالادست (قسمت شماره ۱) و پاییندست (قسمت شماره ۲) جریان در کانال باز به صورت زیر بیان کنیم.
$$\large z_1 \: + \: y_1 \: + \: \frac {V ^2_1} {2 g} \: = \: z_2 \: + \: y_2 \: + \: \frac {V ^2_2} {2 g} \: + \: h_L$$
عبارت $$\large h_L$$ نشاندهنده افت هد است که به دلیل اثرات اصطکاک اتفاق میافتد و مانند جریان در لوله و به شیوه زیر تعریف میشود.
$$\large h_L \: = \: f \: \times \: \frac {L} {D_h} \: \times \: \frac {V^2} {2 g} \: = \: f \: \times \: \frac {L} {R_h} \: \times \: \frac {V^2} {8 g}$$
در رابطه بالا، $$\large f$$ ضریب اصطکاک متوسط و $$\large L$$ نیز طول کانال بین دو نقطه شماره $$1$$ و $$2$$ است.
محرک جریان در کانال باز نیروی گرانش است. به همین دلیل، کانالها با شیبی به سمت پایین ساخته میشوند. این موضوع در شکل زیر نشان داده شده است. شیب کف کانال را با نماد $$\large S_0$$ نشان میدهیم.
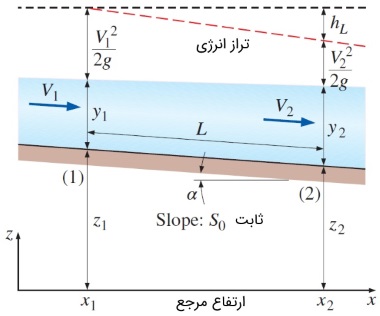
$$\large S_0 \: = \: \tan \alpha \: = \: \frac {z_1 \: - \: z_2} {x_2 \: - \: x_1} \: \cong \: \frac {z_1 \: - \: z_2} {L}$$
در این رابطه، $$\large \alpha$$ زاویهایست که کف کانال با خط افق میسازد. در حالت کلی، شیب کف کانال بسیار کوچک است و میتوان آن را تقریباً افقی در نظر گرفت. از این رو از تقریب $$\large L \: \cong \: x_2 \: - \: x_1$$ استفاده کردیم. مقدار $$\large x$$، فاصله در راستای افقی را نشان میدهد. از طرف دیگر، عمق جریان $$\large y$$ را که در جهت عمودی اندازهگیری میشود، میتوانیم با خطای ناچیزی، برابر عمق عمود به کف کانال تقریب بزنیم. اگر سطح زیرین کانال مستقیم باشد، شیب آن ثابت خواهد بود و کاهش فاصله عمودی بین قسمتهای $$1$$ و $$2$$ به صورت رابطه $$\large z_1 \: - \: z_2 \: = \: S_0 \: L$$ بیان میشود. به این ترتیب، میتوانیم معادله انرژی را به صورت زیر بازنویسی کنیم.
$$\large y_1 \: + \: \frac {V^2 _1} {2 g} \: + \: S_0 \: L \: = \: y_2 \: + \: \frac {V^2 _2} {2 g} \: + \: h_L$$
رابطه اخیر، مستقل از دانستن ارتفاع نقطه مرجع است. شیب کف کانال در طراحی سیستمهای جریان در کانال باز طوری انتخاب میشود تا کاهش ارتفاع مناسبی برای غلبه بر افت هد اصطکاکی داشته باشد. به این ترتیب، دبی جریان در اندازه دلخواه ثابت میماند. از این رو، ارتباط تنگاتنگی بین افت هد و شیب کف کانال برقرار است. پس هنگامی که میخواهیم معادله انرژی جریان در کانال باز را بنویسیم، افت هد را برحسب شیب کف کانال به کار میبریم. بدین منظور، ابتدا باید شیب اصطکاکی (Friction Slope) را به صورت $$\large S_f \: = \: \frac {h_L} {L}$$ تعریف کنیم. به این ترتیب میتوانیم معادله انرژی را به شکل زیر بنویسیم.
$$\large y_1 \: + \: \frac {V^2 _1} {2 g} \: = \: y_2 \: + \: \frac {V^2 _2} {2 g} \: + \: (S_f \: - \: S_0) L$$
همانطور که مشاهده میکنید اگر شیب اصطکاکی با شیب کف کانال برابر باشد، افت هد و کاهش ارتفاع با هم مساوی خواهند بود. به عبارت دیگر، هنگامی که $$\large S_f \: = \: S_0$$ باشد، رابطه $$\large h_L \: = \: z_1 \: - \: z_2$$ نیز برقرار است. در شکل قبل، خط انرژی هم نشان داده شده است. خط انرژی در فاصله $$\large z \: + \: y \: + \: \frac {V^2} {2 g}$$ در بالای خط افقی مرجع قرار دارد و انرژی مکانیکی کل مایع را برحسب هد بیان میکند. خط انرژی مانند کف کانال، دارای شیب است که از افتهای اصطکاکی، کاهش ارتفاع برابر با افت هد و شیب اصطکاکی نتیجه میشود. توجه کنید که اگر افت هد وجود نداشت، خط انرژی به صورت افقی درمیآمد؛ حتی اگر شیب کانال هم صفر نباشد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:
- تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
- فلومتر (Flowmeter) – از صفر تا صد
- ورتکس (Vortex) چیست؟ — به زبان ساده
- جریان تراکم پذیر (Compressible Flow) — اصول و مفاهیم
^^










عالی بود مطالب. ممنون از زحماتی که کشیدید
سلام
با تشکر
لازم به ذکر است که فورمول ها نمایش داده نمیشوند.
با سلام؛
اگر نوع دستگاه (موبایل، کامپیوتر و …) و نوع مرورگر را هم ذکر کنید، میتوانیم بررسی بهتری داشته باشیم.
با تشکر از همراهی شما با مجله فرادرس
دنبال محاسبه ضخامت لایه زیرین آرام در کانال بودم. ولی چیزی نیافتم
بسیار عالی