جریان متغیر تدریجی در کانال باز – از صفر تا صد

قبلاً در مقاله‌ای از مجله فرادرس، جریان در کانال باز را مورد بررسی قرار دادیم. همان‌طور که می‌دانید، جریان کانال باز را می‌توانیم به دو نوع یکنواخت (Uniform) و غیریکنواخت (Nonuniform) تقسیم کنیم. جریان غیریکنواخت که متغیر (Varied)‌ هم نامیده می‌شود، خودش در دو گروه جریان متغیر تدریجی (Gradually Varied Flow) و جریان متغیر سریع (Rapid Varied Flow) جای می‌گیرد. در این مقاله به بررسی جریان متغیر تدریجی و پروفایل سطح مایع در کانال‌های باز خواهیم پرداخت.

جریان متغیر تدریجی که به اختصار $$\large \text{GVF}$$ هم نامیده می‌شود، نوعی از جریان‌های غیر یکنواخت پایدار محسوب می‌شود که در آن، تغییرات سرعت و عمق به آهستگی و به صورت تدریجی انجام می‌شود. سطح آزاد جریان همیشه هموار است و هیچ‌گونه ناپیوستگی یا خطوط شکسته در آن دیده نمی‌شود. جریان‌هایی که در آنها، تغییرات عمق و سرعت، به تندی اتفاق می‌افتد را در دسته جریان‌های متغیر سریع قرار داده و به اختصار با $$\large \text{RVF}$$ نمایش می‌دهند.

وجود هرگونه تغییر در شیب کف کانال، عوض شدن سطح مقطع آن یا وجود مانع در سر راه جریان، موجب می‌شود جریان از حالت یکنواخت به جریان متغیر تدریجی یا سریع تبدیل شود. جریان‌های متغیر سریع، در قسمت کوتاهی از کانال تشکیل می‌شوند و سطح مقطع کوچکی هم دارند. به همین دلیل، افت‌های اصطکاکی ناشی از تنش برشی دیواره‌ها ناچیز است. افت‌های هد در RVF، موضعی بوده و به دلیل آشفتگی و تلاطم شدید رخ می‌دهند. اما در جریان متغیر تدریجی این افت‌ها اساساً به دلیل اثرات اصطکاکی در طول کانال رخ می‌دهند و می‌توان آنها را با کمک فرمول مانینگ تعیین کرد.

تغییرات سرعت و عمق در جریان متغیر تدریجی به کندی انجام می‌شود و سطح آزاد در شرایط پایدار است. همین موضوع کمک می‌کند بتوانیم تغییرات عمق را در طول کانال براساس اصل پایستگی جرم و انرژی فرمول‌بندی کرده و رابطه پروفایل سطح آزاد را استخراج کنیم. در جریان یکنواخت، شیب خط انرژی برابر با شیب سطح زیرین کانال (Bottom Slope) است. بنابراین، شیب اصطکاک با شیب کف کانال برابر بوده و رابطه $$\large S_f \:=\: S_0$$ برقرار است. اما در جریان‌های متغیر (غیریکنواخت) این خطوط شیب‌های متفاوتی دارند.

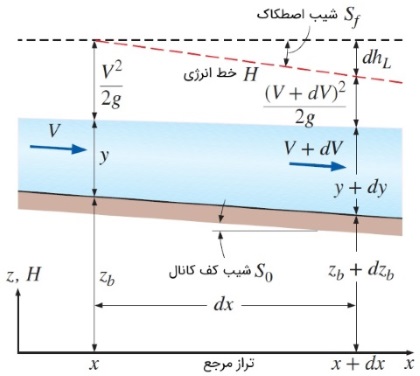
شکل بالا را در نظر بگیرید. جریانی پایدار در یک کانال باز با سطح مقطع مستطیلی برقرار است. عرض کانال برابر با $$\large b$$ بوده و تمام تغییرات در شیب کف کانال و عمق آب، به صورت تدریجی اتفاق می‌افتد. انرژی مکانیکی کل سیال برحسب هد به صورت رابطه زیر نوشته می‌شود.

$$\large H \:=\: z_b \:+\: y\:+ \:\frac {V^2} {2g}$$

در رابطه بالا، $$\large z_b$$ فاصله عمودی سطح زیرین تا تراز افقی مرجع است. توجه کنید که معادلات براساس سرعت متوسط $$\large V$$ نوشته شده و توزیع فشار به صورت هیدرواستاتیکی تقریب زده شده است. از $$\large H$$ نسبت به $$\large x$$ مشتق می‌گیریم.

$$\large \frac {\text {d} H}{ \text {d} x} \:=\: \frac {\text {d}}{ \text {d} x} (z_b \:+\: y\:+ \:\frac {V^2} {2g}) \:=\: \frac {\text {d} z_b}{ \text {d} x} \:+\: \frac {\text {d} y}{ \text {d} x} \:+\: \frac {V} {g} \frac {\text {d} V}{ \text {d} x}$$

همان‌طور که می‌دانیم، $$\large \frac {\text {d} H}{ \text {d} x}$$ برابر با شیب خط انرژی (با مقدار منفی) بوده و برابر با شیب اصطکاکی با علامت منفی است، که این موضوع را در شکل قبل مشاهده می‌کنید. همچنین مقدار $$\large \frac {\text {d} z_b}{ \text {d} x}$$ نیز با منفیِ شیب کف کانال برابر است.

$$\large \frac {\text {d} H}{ \text {d} x} \:=\: -\:\frac {\text {d} h_L} {\text {d} x}\: =\:- \:S_f \\~\\
\large \frac {\text {d} z_b} {\text {d} x}\: =\:-\: S_0$$

با ادغام سه رابطه اخیر، رابطه زیر حاصل می‌شود.

$$\large S_0 \:-\: S_f\: =\:\frac {\text {d} y}{ \text {d} x} \:+\:\frac {V} {g} \frac {\text {d} V}{ \text {d} x}$$

براساس اصل پایستگی جرم برای جریان پایدار در کانالی با سطح مقطع مربع، عبارت $$\large \dot{ V}\:=\: ybV$$ مقدار ثابتی دارد. از این رابطه، نسبت به $$\large x$$ مشتق می‌گیریم.

$$\large bV \frac {\text {d} y}{ \text {d} x}\: +\:yb\frac {\text {d} V}{ \text {d} x} \:=\:0 \\~\\
\large \Rightarrow ~~~ \frac {\text {d} V}{ \text {d} x}\:=\: -\:\frac {V} {y} \frac {\text {d} y}{ \text {d} x}$$

اکنو با دقت در دو رابطه آخر و استفاده از تعریف عدد فرود (Froude Number) که برابر با $$\large V/\sqrt {gy}$$ است، عبارت زیر را نتیجه می‌گیریم.

$$\large S_0 \:{-}\: S_f \:{=}\: \frac {\text {d} y}{ \text {d} x} \:{-}\: \frac {V^2} {gy} \frac {\text {d} y}{ \text {d} x}{} \:{=}\: \frac {\text {d} y}{ \text {d} x}{} \:{-}\: {Fr}^2 \frac {\text {d} y}{ \text {d} x}$$

ما به دنبال نرخ تغییرات عمق آب در طول کانال (یا پروفایل سطح آزاد) در جریان متغیر تدریجی هستیم. در نتیجه، معادله بالا را برحسب $$\large \frac {\text {d} y}{ \text {d} x}$$ مرتب می‌کنیم. معادله زیر به معادله جریان متغیر تدریجی یا معادله $$\large \text {GVF}$$ معروف است.

$$\large \frac {\text {d} y}{ \text {d} x}\: {=}\: \frac {S_0 \:{-}\: S_f} {1 \:{-}\: {Fr}^2}$$

(رابطه ۱)

معادله $$\large \text {GVF}$$ با تغییرات سطح مقطع جریان به عنوان تابعی از عدد ماخ در جریان تراکم پذیر قابل مقایسه است. این رابطه برای کانال باز با سطح مقطع مربعی استخراج شد ولی برای سایر کانال‌ها هم معتبر است. با این شرط که سطح مقطع کانال ثابت باشد و بتوان عدد فرود را در طول کانال تعریف کرد. با حل این معادله دیفرانسیل، می‌توانیم عمق جریان $$\large y$$ را به عنوان تابعی از $$\large x$$ استخراج کنیم. تابع $$\large y(x)$$، پروفایل سطح آزاد هم نامیده می‌شود.

روند تغییرات کلی عمق جریان (چه افزایشی باشد، چه کاهشی باشد و چه در طول کانال ثابت بماند) به علامت $$\large \frac {\text {d} y}{ \text {d} x}$$ بستگی دارد؛ که علامت $$\large \frac {\text {d} y}{ \text {d} x}$$ هم تحت تأثیر صورت و مخرج رابطه ۱ است. عدد فرود همیشه مثبت است. علاوه بر آن، شیب اصطکاک $$\large S_f$$ نیز هیچ‌گاه منفی نخواهد بود (در شرایط ایده‌آلی که بتوانیم از اصطکاک صرف نظر کنیم، $$\large h_L$$ و $$\large S_f$$ صفر هستند).

بنا به قرارداد، اگر شیب قسمتی از کانال رو به پایین باشد، آن را مثبت می‌نامیم. اگر سطح زیرین کانال افقی باشد، شیب آن قسمت صفر است. همچنین شیب منفی اشاره به قسمتی از کانال دارد که با شیب رو به بالا ساخته شده باشد. از طرف دیگر، هنگامی که عمق کانال افزایش یابد، مقدار $$\large \frac {\text {d} y}{ \text {d} x}$$ مثبت است و مقدار منفی $$\large \frac {\text {d} y}{ \text {d} x}$$ نشان می‌دهد که عمق کانال کاهش یافته است. زمانی هم که $$\large \frac {\text {d} y}{ \text {d} x}$$ ثابت باشد، عمق کانال بدون تغییر می‌ماند. در حالت سوم، سطح آزاد آب، مشابه جریان یکنواخت، موازی با تراز مرجع است.

اگر مقادیر $$\large S_0$$ و $$\large S_f$$ مشخص باشد، عبارت $$\large \frac {\text {d} y}{ \text {d} x}$$ ممکن است منفی یا مثبت شود. اینکه عدد فرود، کوچکتر یا بزرگتر از عدد یک باشد، در این مورد، تعیین کننده خواهد بود. بنابراین، رفتار جریان در حالت‌های زیر بحرانی و فوق بحرانی، متفاوت است. به عنوان مثال، در حالتی که $$\large S_0 \:{-}\: S_f \:{>}\: 0$$ باشد، عمق جریان در جهت جریان زیر بحرانی افزایش می‌یابد. حال آنکه اگر جریان فوق بحرانی باشد، عمق در جهت جریان کم می‌شود.

تعیین علامت مخرج کسر کار ساده‌ایست. اگر عدد فرود کوچکتر از یک باشد، مقدار $$\large 1\:-\: (Fr)^2$$ مثبت است. ولی اگر عدد فرود بزرگتر از یک باشد، مقدار این عبارت، منفی می‌شود. اما برای اینکه علامت صورت کسر مشخص شود، اندازه نسبی $$\large S_0$$ و $$\large S_f$$ باید معلوم باشد. مقدار شیب اصطکاک $$\large S_f$$ همیشه مثبت بوده و مقدار آن با مقدار شیب کانال $$\large S_0$$ در جریان یکنواخت $$\large y\:=\: y_n$$ برابر است. شیب اصطکاک، کمیتی است که اندازه آن با فاصله جریان عوض می‌شود. برای محاسبه آن باید از معادله مانینگ براساس عمق هر نقطه از جریان استفاده شود.

توجه کنید که افت هد با بالارفتن سرعت، افزایش می‌یابد و سرعت هم به صورت معکوس با عمق جریان متناسب است. در یک نرخ دبی مشخص، اگر $$\large y\:<\: y_n$$ باشد، آنگاه نامساوی $$\large S_f\:>\: S_0$$ برقرار است و اگر $$\large y\:>\: y_n$$ باشد، نامساوی به صورت $$\large S_f\:<\: S_0$$ خواهد بود. می‌توان این‌گونه نتیجه گرفت که برای کانال‌هایی با شیب صفر یا شیب مثبت، مقدار $$\large S_0\:-\: S_f$$ همیشه منفی است و اگر جریان مورد نظر، زیر بحرانی باشد، عمق در جهت جریان کاهش پیدا می‌کند.

پروفایل سطح مایع در جریان متغیر تدریجی

طراحی و ساخت سیستم‌های کانال باز، براساس عمق جریان تصویر شده در طول مسیر انجام می‌شود. بنابراین، توانایی پیش‌بینی عمق جریان از روی نرخ دبی حجمی و هندسه کانال، اهمیت بالایی دارد. نمودار عمق جریان برحسب فاصله پایین‌دست، به عنوان پروفایل سطح مایع شناخته می‌شود و آن را به صورت $$\large y(x)$$ نشان می‌دهیم. مشخصات کلی پروفایل‌های سطح در جریان متغیر تدریجی به شیب کف کانال و نسبت عمق جریان به عمق بحرانی و عمق قائم بستگی دارد.

یک کانال باز واقعی، از قسمت‌های مختلفی تشکیل شده که هر کدام شیب $$\large S_0$$ متفاوت و رژیم‌های جریان گوناگونی دارند. در نتیجه، پروفایل سطح در هر یک از قسمت‌ها با دیگری متفاوت است. به عنوان مثال، شکل کلی پروفایل سطح در قسمتی از کانال که شیب رو به پایین دارد، در مقایسه با قسمت دیگری که شیب آن به سمت بالاست، یکسان نیست. به همین ترتیب، پروفایل جریان زیر بحرانی هم با پروفایل جریان فوق بحرانی تفاوت دارد. برخلاف جریان یکنواخت که هیچ نیروی اینرسی در آن دخالت نمی‌کند، شتاب‌های مثبت و منفی بسیاری در جریان متغیر تدریجی مشاهده می‌شود. پروفایل سطح، تعادل دینامیکی بین وزن مایع، نیروی برشی و اثرات اینرسی را منعکس می‌کند.

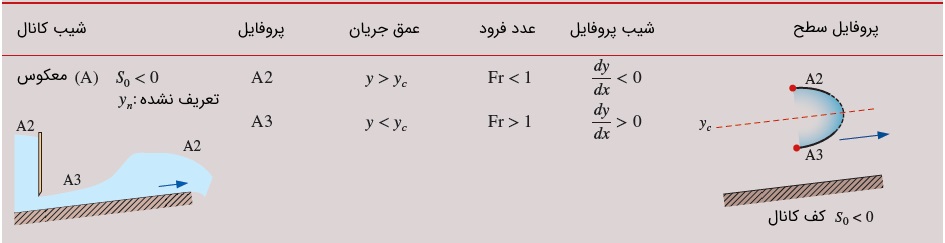
هر پروفایل سطح، با یک حرف انگلیسی و یک عدد نشان داده می‌شود. شیب کانال با کمک حرف انگلیسی و نسبت عمق جریان به عمق بحرانی $$\large y_c$$ و عمق قائم $$\large y_n$$ با عدد تعریف می‌شود. شیب کانال به پنج دسته تند (Steep)، بحرانی (Critical)، ملایم (Mild)، افقی (Horizontal) و معکوس (Adverse) تقسیم می‌شود. شکل زیر، این پنج دسته را نشان می‌دهد. اگر $$\large y_n \:>\: y_c$$ برقرار باشد، شیب کانال، ملایم و اگر $$\large y_n \:<\: y_c$$ باشد، شیب آن تند است. هنگامی که $$\large y_n \:=\: y_c$$ باشد، شیب کانال بحرانی خوانده می‌شود. در دو حالت شیب افقی و معکوس نیز به ترتیب رابطه‌های $$\large S_0 \:=\:0$$ و $$\large S_0 \:<\:0$$ (شیب منفی) برقرار هستند.

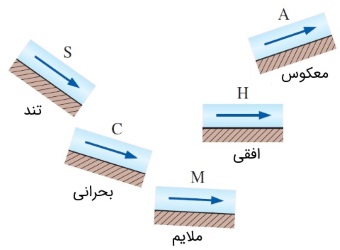
دسته‌بندی هر قسمت از کانال به نرخ دبی حجمی، سطح مقطع کانال و شیب کانل وابسته است. به عبارت دیگر، اگر قسمتی از کانال برای یک جریان خاص، در دسته شیب ملایم قرار بگیرد، ممکن است در جریان دیگری شیب تند داشته باشد و برای یک جریان سوم، شیب آن بحرانی شود. در واقع پیش از اینکه شیب کانال را بررسی کنیم، باید عمق بحرانی $$\large y_c$$ و عمق قائم $$\large y_n$$ محاسبه شود.

عددی که به هر پروفایل سطح اختصاص داده می‌شود، با فرض مشخص بودن شیب کانال مربوط به ارتفاع سطح در جریان‌های بحرانی و یکنواخت، موقعیت اولیه سطح مایع را مشخص می‌کند. شکل زیر را در نظر بگیرید. اگر عمق جریان، بالاتر از عمق بحرانی و عمق قائم ($$\large y\:>\: y_c$$ و $$\large y\:>\: y_n$$) باشد، شاخص پروفایل سطح، عدد یک خواهد بود. هرگاه عمق جریان بین دو عمق بحرانی و عمق قائم ($$\large y_n \:>\:y\:>\: y_c$$ و $$\large y_n \:<\:y\:<\: y_c$$) قرار بگیرد، شاخص پروفایل سطح، عدد دو است. در نهایت، هنگامی که عمق جریان، پایین‌تر از دو عمق بحرانی و قائم ($$\large y\:<\: y_c$$ و $$\large y\:<\: y_n$$) باشد، با شاخص سه نشان داده می‌شود.

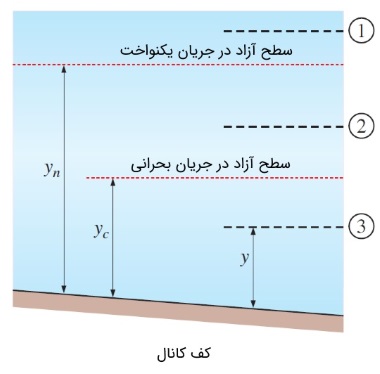
بنابراین، برای هر دسته از شیب کانال، سه پروفایل مختلف امکان‌پذیر است. توجه کنید که برای شیب‌های افقی و معکوس، نوع جریان شماره یک امکان‌پذیر نیست. زیرا جریان نمی‌تواند در کانال‌های افقی و رو به بالا، یکنواخت باشد. از این رو، عمق قائم در چنین حالتی تعریف ناپذیر است. از طرف دیگر در کانال‌هایی با عمق بحرانی، جریان شماره دو وجود ندارد. زیرا در این حالت، دو عمق بحرانی و قائم یکی هستند.

تا اینجا پنج دسته برای شیب و سه شاخص عددی برای موقعیت اولیه جریان برشمردیم. با حذف حالت‌های غیرممکن، در مجموع می‌توان دوازده حالت مختلف برای پروفایل سطح در جریان متغیر تدریجی در نظر گرفت. این حالت‌ها را در ادامه به اختصار بررسی می‌کنیم. توجه کنید که هرجا $$\large \frac {\text {d} y}{ \text {d} x}>0$$ باشد، عمق مایع در جهت جریان افزایش می‌یابد و در واقع هر دو عبارت $$\large S_0 \:-\:S_f$$ و $$\large 1\:-\: Fr^2$$ به طور همزمان مثبت یا منفی هستند. در جریان نوع یک، عمق در جهت جریان زیاد می‌شود و پروفایل سطح به صورت متناوب به صفحه افقی می‌رسد. در جریان نوع دو، عمق جریان کاهش می‌یابد و پروفایل سطح از بین عمق بحرانی و عمق قائم به هرکدام که کمتر باشد، می‌رسد. در جریان نوع سه، عمق جریان افزایش می‌یابد و پروفایل سطح از بین عمق بحرانی و عمق قائم به مقداری که کمتر است خواهد رسید. این الگو در پروفایل‌های سطح تا جایی که تغییری در شیب و زبری سطح رخ ندهد ادامه خواهد داشت.

شیب تند (Steep Slope)

جدول زیر، مشخصات جریانی را نشان می‌دهد که در دسته شیب تند قرار گرفته است. همان‌طور که می‌بینید در این دسته، هر سه نوع جریان امکان‌پذیر است و آنها را با $$\large S_1$$، $$\large S_2$$ و $$\large S_3$$ مشخص کرده‌ایم. هر سه پروفایل سطح، به صورت شماتیک رسم شده است.

شیب بحرانی (Critical Slope)

همان‌طور که گفتیم در این حالت، عمق بحرانی با عمق قائم برابر است. مشخصات جریانی که در آن شیب کانال، بحرانی است را در جدول زیر مشاهده می‌کنید. در این دسته، فقط دو نوع پروفایل سطح رخ می‌دهد که آنها را با $$\large C_1$$ و $$\large C_3$$ نشان داده‌ایم.

شیب ملایم (Mild Slope)

سومین دسته از شیب‌های کانال، شیب ملایم است. مشخصه‌های شیب ملایم در جدول زیر ارائه شده است. تشکیل هر سه پروفایل سطح در این دسته امکان پذیر است. این سه پروفایل عبارت از $$\large M_1$$، $$\large M_2$$ و $$\large M_3$$ هستند. نکته جالب توجه در این مورد، تقارن پروفایل‌های سطح $$\large M_2$$ و $$\large M_3$$ نسبت به عمق بحرانی است.

شیب افقی (Horizontal Slope)

جدول زیر، مشخصات جریانی را نشان می‌دهد که در دسته شیب افقی قرار گرفته است. همان‌طور که پیش از این گفتیم، در این دسته $$\large S_0 \:=\:0$$ و $$\large y_n \:\rightarrow \:\infty$$ برقرار است. در این دسته، فقط دو نوع جریان امکان‌پذیر است که آنها را با $$\large H_2$$ و $$\large H_3$$ مشخص کرده‌ایم. هر دو پروفایل سطح، به صورت شماتیک رسم شده است. در این حالت هم دو پروفایل سطح، نسبت به عمق بحرانی، متقارن هستند.

شیب معکوس (Adverse Slope)

بالاخره آخرین دسته از انواع شیب کانال، شیب معکوس است. به جدول زیر توجه کنید. در این حالت، عمق قائم تعریف نمی‌شود و دو پروفایل سطح ممکن را با $$\large A_2$$ و $$\large A_3$$ نشان می‌دهیم.

به عنوان مثالی از جدول‌های بالا، حالت $$\large M_1$$ را در نظر بگیرید. در این حالت، شیب کانال، ملایم است و عمق جریان در رابطه $$\large y\:>\: y_n \:>\: y_c$$ صدق می‌کند. از آنجایی که $$\large y\:>\: y_c$$ است، جریان زیر بحرانی به شمار می‌رود. در نتیجه، $$\large Fr <1$$ و همچنین $$\large 1- Fr^2 >0$$ برقرار هستند. از طرف دیگر، به دلیل اینکه $$\large y>y_n$$، رابطه‌های $$\large S_f< S_0$$ و $$\large S_0- S_f>0$$ نیز نتیجه گرفته می‌شوند. بنابراین، شیب پروفایل سطح به صورت زیر خواهد بود.

$$\large \frac {\text {d} y}{ \text {d} x}\:=\: (S_0\:-\: S_f)/ (1\:-\: Fr^2) \:>\:0$$

از این رو، عمق $$\large y$$ در جهت جریان افزایش می‌یابد. ولی با افزایش $$\large y$$، سرعت جریان کم می‌شود و مقادیر $$\large S_f$$ و عدد فرود به سمت صفر میل می‌کنند. در نهایت، $$\large \frac {\text {d} y}{ \text {d} x}$$ به $$\large S_0$$ میل کرده و نرخ افزایش عمق جریان با شیب کانال برابر خواهد شد. بدین منظور، پروفایل سطح باید در عمق زیاد $$\large y$$، افقی شود. این گونه نتیجه می‌گیریم که پروفایل سطح $$\large M_1$$ در جهت جریان بالا آمده و به یک خط مجانب افقی میل خواهد کرد.

در جریان زیر بحرانی، اگر $$\large y\:\rightarrow\: y_c$$ باشد (مانند آنچه در $$\large M_2$$، $$\large H_2$$ و $$\large A_2$$ وجود دارد)، عدد فرود به سمت عدد یک رفته و $$\large 1-Fr^2 \rightarrow 0$$ خواهد بود. در این حالت، شیب $$\large \frac {\text {d} y}{ \text {d} x}$$ به سمت منفی بینهایت میل می‌کند. اما اگر در جریان فوق بحرانی $$\large y\:\rightarrow\: y_c$$ باشد (مانند آنچه در $$\large M_3$$، $$\large H_3$$ و $$\large A_3$$ اتفاق می‌افتد)، عدد فرود به سمت یک و $$\large 1-Fr^2$$ به صفر میل می‌کند و در نتیجه، شیب $$\large \frac {\text {d} y}{ \text {d} x}$$ به سمت مثبت بینهایت میل خواهد کرد. به عبارت دیگر، سطح آزاد جریان تقریباً به صورت عمودی بالا می‌آید و عمق جریان به سرعت افزایش می‌یابد. از نظر فیزیکی احتمال وقوع چنین پدیده‌ای وجود ندارد. در نتیجه، سطح آزاد شکسته می‌شود و پرش هیدرولیکی رخ می‌دهد. در این وضعیت، دیگر فرض جریان تک‌بعدی اعتبار ندارد.

مروری بر چند پروفایل رایج سطح در جریان متغیر تدریجی

سیستم‌های کانال باز واقعی از چند قسمت با شیب‌های مختلف تشکیل می‌شوند. به محل اتصال این قسمت‌ها، ناحیه گذار یا انتقال می‌گویند. در نتیجه، پروفایل کلی سطح جریان، پروفایل پیوسته‌ایست که از کنار هم قرار گرفتن پروفایل‌های ساده‌ای که تا به اینجا توضیح دادیم، تشکیل می‌شود. در هر مرحله، به دلیل وجود تغییراتی در هندسه کانال، پروفایل سطح عوض می‌شود. هر نقطه روی پروفایل سطح، نشان دهنده عمق جریان در آن نقطه است.

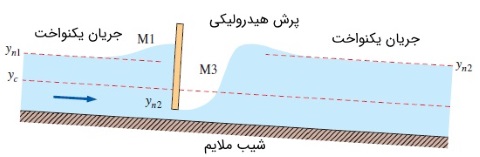
شکل زیر، پروفایل سطح را برای جریان متغیر تدریجی در یک کانال نشان می‌دهد. شیب کانال، ملایم است و جریان از یک دریچه سد عبور می‌کند. جریان بالادست در حالت زیر بحرانی قرار دارد و به محض رسیدن به دریچه، سرعتش کم و ارتفاعش زیاد می‌شود. به عنوان مثال می‌توانید رودخانه‌ای را در نظر بگیرید که به سد می‌رسد. جریان پس از عبور از دریچه، به حالت فوق بحرانی تبدیل می‌شود. زیرا ارتفاع ورودی سد کمتر از عمق بحرانی است. در نتیجه، پروفایل سطح، قبل از دریچه $$\large M1$$ و پس از دریچه $$\large M3$$ است. پس از $$\large M3$$ نیز پرش هیدرولیکی اتفاق می‌افتد.

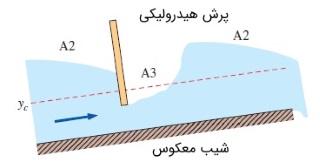
ممکن است در قسمتی از کانال، شیب منفی بوده و جهت حرکت جریان رو به بالا باشد. شکل زیر، جریان با شیب معکوس را نشان می‌دهد. شیب معکوس تنها در حالتی ادامه پیدا می‌کند که نیروهای اینرسی به گرانش و نیروهای ویسکوز غلبه کند. بنابراین، در ادامه قسمتی از کانال که رو به بالا است، باید بلافاصله، یک قسمت رو به پایین قرار بگیرد یا جریان به صورت آزاد خارج شود. اگر جریان زیر بحرانی در یک شیب معکوس به دریچه سد برسد، بلافاصله پس از رسیدن به دریچه، عمق جریان کاهش می‌یابد و پروفایل سطح در حالت $$\large A2$$ دسته‌بندی می‌شود. پس از دریچه، جریان فوق بحرانی می‌شود و پیش از پرش هیدرولیکی، پروفایل سطح $$\large A3$$ می‌شود.

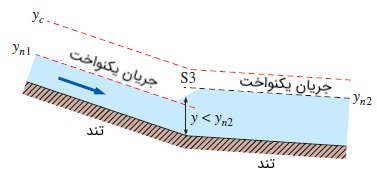
در بخشی از کانال که در شکل پایین نشان داده شده است، شیب هر دو قسمت تند است. در قسمتی که شیب کمتری دارد، سرعت جریان کمتر است و هنگامی که جریان دوباره یکنواخت می‌شود، عمق جریان بیشتر می‌شود. به این نکته توجه کنید که جریان یکنواخت در شیب تند، حتماً باید از نوع فوق بحرانی ($$\large y<y_c$$) باشد و عمق جریان بین دو حالت یکنواخت، در نقطه $$\large S3$$ و به صورت هموار، افزایش می‌یابد.

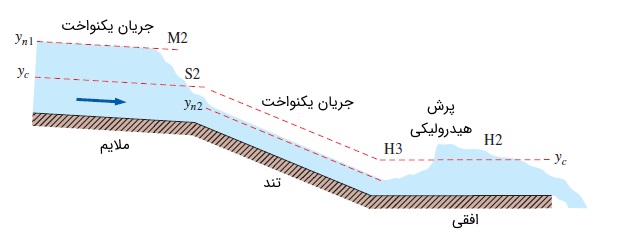
شکل بعدی، پروفایل سطح مرکبی را نشان می‌دهد. این کانال باز از سه قسمت مختلف ساخته شده است. شیب قسمت اول، ملایم بوده و جریان از نوع یکنواخت و زیر بحرانی است. سپس شیب ملایم به شیب تند تغییر می‌کند و با جریان یکنواخت و بحرانی مواجه می‌شویم. در قسمت افقی، عمق جریان در ابتدا آرام آرام به پروفایل $$\large H3$$ می‌رسد و پس از آن، به سرعت، پرش هیدرولیکی رخ می‌دهد. سپس با شتاب گرفتن جریان به سمت انتهای کانال، عمق جریان به صورت تدریجی کاهش پیدا می‌کند.

حل عددی پروفایل سطح در جریان متغیر تدریجی

پیش‌بینی پروفایل سطح $$\large y(x)$$، مرحله مهمی در طراحی سیستم‌های کانال باز است. اولین گام در تعیین پروفایل سطح، شناسایی نقاطی در طول کانال است که آنها را تحت عنوان نقاط کنترل تعریف می‌کنیم. در نقاط کنترل (Control Points) با داشتن نرخ دبی حجمی، می‌توان عمق جریان را محاسبه کرد. به عنوان مثال، در قسمتی از یک کانال با مقطع مستطیلی که در آن، جریان بحرانی رخ می‌دهد، نقطه بحرانی نامیده می‌شود. عمق جریان در نقطه بحرانی به صورت زیر محاسبه می‌شود.

$$\large y_c\: =\:(\frac {{\dot{V}}^2} {gb^2}) ^{1/3}$$

عمق قائم $$\large y_n$$، به عنوان نمونه دیگری از نقطه کنترل شناخته می‌شود. هنگامی که جریان یکنواخت می‌شود، جریان به عمق قائم می‌رسد. اگر عمق‌های جریان در نقاط کنترل مشخص باشند، پروفایل سطح در بالادست و پایین‌دست قابل محاسبه است. بدین منظور باید از معادله دیفرانسیل غیرخطی زیر، انتگرال معین گرفته شود.

$$\large \frac{ \text {d} y}{ \text {d} x}\:=\: \frac {S_0\:-\: S_f} {1\:-\: Fr^2}$$

برای تعیین شیب اصطکاکی $$\large S_f$$ از شرایط جریان در حالت یکنواخت کمک می‌گیریم و عدد فرود از معادلات مربوط به سطح مقطع کانال محاسبه می‌شود.

مثال ۱: جریان متغیر تدریجی با پروفایل سطح M1

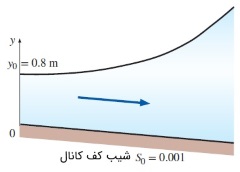
سؤال: آب به صورت یک جریان متغیر تدریجی در کانالی عریض در حرکت است. نرخ دبی حجمی در واحد عرض کانال و ضریب مانینگ به ترتیب برابر $$\large 1\: m^3/s.m$$ و $$\large n\:=\: 0.02$$ هستند. شکل زیر را در نظر بگیرید. شیب کانال $$\large n\:=\: 0.001$$ است و در نقطه $$\large x\:=\: 0$$، عمق جریان به $$\large 0.8\:m$$ می‌رسد.

الف) عمق قائم و عمق بحرانی جریان را مشخص و پروفایل سطح آب را تعیین کنید.

ب) با محاسبه انتگرال معین از معادله $$\large \text{ GVF}$$ در دامنه $$\large 0\:\leq \:x\:\leq \:1000\:m$$، عمق جریان $$\large y$$ را به دست آورید.

پ) مرحله ب را برای مقادیر مختلف $$\large x$$ محاسبه و نمودار پروفایل سطح را رسم کنید.

پاسخ: عرض کانال بسیار زیاد است. در نتیجه، عمق هیدرولیکی با عمق جریان برابر است ($$\large R_h\: \cong\:y$$). حال، با داشتن نرخ دبی حجمی در واحد عرض ($$\large b\:=\: 1\:m$$) عمق قائم را با کمک رابطه مانینگ به دست می‌آوریم.

$$\large \dot {V} \:=\:\frac {a} {n} A_c R_h^ {2/3} S_0^ {1/2} \:=\:\frac {a} {n} (yb) y^{2/3} S_0^ {1/2} \\~\\
\large \dot {V} \:=\:\frac {a} {n} by^ {5/3} S_0^ {1/2} \\~\\
\large \Rightarrow y_n\:=\: (\frac {(\dot {V}/b )n} {aS _0^{ 1/2}}) ^{3/5} \\~\\
\large y_n\:=\: (\frac {(1\:m ^2/s) (0.02)} {(1\: m^{1 /3}/s) (0.00 1)^{1 /2}}) ^{3/5} \:=\:0.7 6\:m$$

عمق بحرانی با استفاده از رابطه زیر محاسبه می‌شود.

$$\large y_c\:=\: \frac {{\dot {V}}^2} {gA_ c^2}\:=\: \frac {{\dot {V}}^2} {g(by _c)^2} \\~\\
\large y_c\:=\: (\frac {(\dot{V}/b)^2} {g}) ^{1/3}\:=\: (\frac {(1\:m^2/s)^2} {9.81 \:m/s^2}) ^{1/3} \\~\\
\large \Rightarrow ~~~ y_c\:=\:0.47\:m$$

همان‌طور که می‌بینید، در نقطه $$\large x\:=\:0$$، رابطه $$\large y_c<y_n<y$$ برقرار است. با دقت در جدول‌هایی که در این مقاله مشاهده کردید، نتیجه می‌گیریم پروفایل سطح آب در این جریان متغیر تدریجی از نوع $$\large \text {M1}$$ است.

ب) با استفاده از شرط اولیه $$\large y(0)\:=\: 0.8\:m$$، می‌توانیم با محاسبه انتگرال معین معادله جریان متغیر تدریجی عمق جریان $$\large y$$ را در هر نقطه $$\large x$$ تعیین کنیم.

$$\large \frac{\text {d} y}{ \text {d} x}\:=\: \frac {S_0\:-\: S_f} {1\:-\: Fr^2}$$

عدد فرود برای کانال عریض با سطح مقطع مستطیلی به شکل زیر محاسبه می‌شود.

$$\large Fr\:=\: \frac {V} {\sqrt{gy}}\:=\: \frac {\dot {V} /by} {\sqrt {gy}}\:=\: \frac {\dot {V}/b} {\sqrt {gy^3}}$$

در معادله جریان یکنواخت، با قرار دادن $$\large S_0=S_f$$، شیب اصطکاکی تعیین می‌شود.

$$\large \dot{V}\:=\: \frac {a} {n} by^ {5/3} S^{1/ 2}_f \\~\\
\large \Rightarrow ~~~ S_f\:=\: (\frac {(\dot {V}/b)n} {ay^ {5/3 }})^2 \:=\:\frac {(\dot{V}/b)^2 n^2} {a^2y^ {10/3}}$$

با جایگذاری این مقادیر، معادله جریان متغیر تدریجی را به صورت رابطه زیر می‌نویسیم.

$$\large \frac{ \text {d} y}{ \text {d} x}\:=\: \frac {S_0\:-\: (\dot {V} /b)^2 n^2/ (a^2y^ {10/3})} {1\:-\: (\dot {V} /b) ^2/ (gy ^3)}$$

درجه غیرخطی بودن رابطه بالا، بسیار زیاد است. به همین دلیل، نمی‌توانیم با روش‌های تحلیلی، انتگرال آن را محاسبه کنیم. ولی استفاده از نرم‌افزارهایی مانند متلب یا $$\large \text {EES}$$، امکان محاسبه انتگرال معادلات دیفرانسیل غیرخطی را به روش‌های عددی فراهم کرده است. به این ترتیب، پاسخ معادله دیفرانسیل غیرخطی مرتبه اول با شرط اولیه $$\large y(x_1)\: =\:y_1$$ به صورت زیر خواهد بود.

$$\large f(x,y)\:=\: \frac {S_0\:-\: (\dot{V}/b)^2 n^2/ (a^2 y^{10/3})} {1\:-\: (\dot{V}/b) ^2/ (gy^3)} \\~\\
\large y\:=\: y_1\:+\: \int_ {x_1} ^{x_2} f(x,y) \text {d}x $$

عمق آب در موقعیت $$\large x$$ با $$\large y= y(x)$$ نشان داده شده است. با حل عددی انتگرال بالا، عمق آب در نقطه $$\large 1000\:m$$ به دست می‌آید.

$$\large y(x_2)\:=\: y(1000\:m) \:=\:1.44\:m$$

با تکرار محاسبات در موقعیت‌های مختلف $$\large x_2$$، می‌توانیم عمق نقاط گوناگون را در طول کانال به دست آوریم. نمودار رسم شده با کمک این نقاط را در شکل زیر مشاهده می‌کنید.

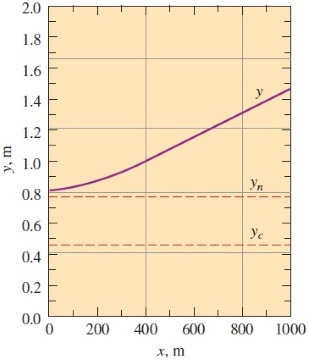
همان‌طور که در قسمت معرفی شیب ملایم (Mild Slope) گفته شد، عمق جریان پروفایل سطح $$\large M1$$ در جهت پایین‌دست، افزایش می‌یابد.

مثال ۲: دسته‌بندی شیب کانال در جریان متغیر تدریجی

سؤال: کانال باز با مقطع مستطیلی نشان داده شده در شکل زیر را در نظر بگیرید. سطوح این کانال، از جنس بتن و پرداخت‌نشده است و آب به صورت یکنواخت در آن جریان دارد. عرض کانال و عمق جریان را به ترتیب $$\large 6\:m$$ و $$\large 2\:m$$ فرض کنید. شیب کانال برابر $$\large 0.004$$ است. شیب این کانال، بین ملایم، بحرانی یا تند، در کدام دسته قرار می‌گیرد. ضریب مانینگ را برای این مسأله برابر با $$\large n=0.014$$ در نظر بگیرید.

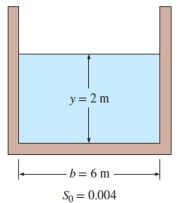
پاسخ: ابتدا مساحت مقطع، محیط و شعاع هیدرولیکی را محاسبه می‌کنیم.

$$\large A_c\: =\:yb\:=\: (2\:m) (6\:m) \:=\:12\: m^2 \\~\\
\large p\:=\: b\:+\: 2y\:=\: 6\:m\:+\: 2(2\:m) \:=\:10\:m \\~\\
\large R_h\:=\: \frac {A_c} {p}\:=\: \frac {12\: m^2} {10\:m} \:=\:1 .2\:m$$

با استفاده از معادله مانینگ، نرخ دبی حجمی به دست می‌آید.

$$\large \dot{V}\:=\: \frac {a} {n} A_c R_h ^{2/3} S_0 ^{1/2}\;=\: \frac {1\:m ^{1/ 3}/s} {0.014} (12\: m^2) (1.2 \:m)^ {2/3} (0.004) ^{1/2} \:=\:61 .2\:m^ 3/s$$

از آنجایی که جریان در حالت یکنواخت قرار دارد، عمق جریان با عمق بحرانی برابر است.

$$\large y\:=\: y_n \:=\:2\:m$$

عمق بحرانی در این جریان از رابطه زیر حاصل می‌شود.

$$\large y_c\:=\: \frac {{\dot {V}}^2} {gA_ c^2}\:=\: \frac {(61.2\: m^3/s) ^2}{(9 .81\:m /s^2) (12\:m ^2)^2} \:=\:2. 65\:m$$

همان‌طور که محاسبه کردیم، $$\large y_n<y_c$$ برقرار است. در نتیجه، شیب کانال در دسته شیب تند قرار می‌گیرد و جریان فوق بحرانی است. اگر عمق جریان بیش از $$\large 2. 65\:m$$ بود، شیب کانال در دسته ملایم قرار می‌گرفت. بنابراین، شیب سطح زیرین کانال به تنهایی برای تعیین ملایم، بحرانی یا تند بودن یک شیب کافی نیست.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
• جریان یکنواخت در کانال باز – به زبان ساده
• ورتکس (Vortex) چیست؟ — به زبان ساده
• جریان تراکم‌ پذیر (Compressible Flow) — اصول و مفاهیم

^^