ورتکس (Vortex) یا گردابه در مکانیک سیالات – به زبان ساده

در راستای ارائه مفاهیم مرتبط با مکانیک سیالات در این قسمت قصد داریم تا در مورد مفهومی صحبت کنیم که عاملی مهم در طراحی وسایل پرنده و دیگر لوازم مبتنی بر سیالات محسوب می‌‌شود. این مفهوم ورتکس یا گردابه نام دارد. همچنین جهت درک بهتر موضوع پیشنهاد می‌شود مطالب توربولانس، سینماتیک سیالات و ویسکوزیته را مطالعه فرمایید.

ورتکس چیست؟

ورتکس (Vortex) یا گردابه به چرخش دایر‌ه‌ای بخشی از سیال حول یک محور ثابت گفته می‌شود. این چرخش منجر به مکیدن اجزایی می‌شود که در اطراف سیالِ در حال چرخش قرار دارد. سرعت چرخش جریان در مرکز بیشترین مقدار بوده و با فاصله گرفتن از آن کاهش می‌یابد. توجه داشته باشید که در این متن از هر دو نام گردابه و ورتکس به منظور اشاره به این مفهوم استفاده شده است.

جریان آبی که به درون سینک ریخته می‌شود تا طوفان‌های عظیم و حتی چشم سرخ مشتری همگی نمونه‌هایی از ورتکس هستند.

مثال‌هایی از گردابه

همان‌طور که در بالا نیز بیان شد گردابه می‌تواند به صورت جریانی چرخشی از سیالی گازی یا مایع در نظر گرفته شود. امواج جزر و مد دریا نوعی گردابه محسوب می‌شوند؛ جریان آبی که به درون سینک ریخته می‌شود تا طوفان‌های عظیم و حتی چشم سرخ مشتری همگی نمونه‌هایی معروف از ورتکس هستند. در بیشتر موارد این جریان‌های توربولانس هستند که منجر به ایجاد ورتکس می‌شوند. بهترین مثال‌‌های بصریِ ورتکس، گردباد‌ها و طوفان‌های شدید هستند. معمولا شکل این گردباد‌ها به صورت ستونی، حلزونی یا مارپیچی است.

در فیزیک هواشناسی «میان‌گردابه» (Mesovortex) به گردابه‌هایی گفته می‌شود که اندازه آن‌ها از مرتبه مایل است. این گردابه‌ها از گردباد‌ها (Tornado)، بزرگ‌تر و از طوفان‌های عظیم (Hurricane) کوچک‌تر هستند. توجه داشته باشید که گردابه علاوه بر مکانیک سیالات در دیگر مفاهیم مهندسی نیز کاربرد دارد. معروف‌ترین نمونه‌های گردابه در ادامه بیان شده‌اند:

فیلم مجموعه آموزش مکانیک سیالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

• میدان‌های الکترومغناطیسی: در بیان هیدرودینامیکی میدان مغناطیسی، شتاب سیال الکتریکی در جهت پادساعتگرد، گردابه‌ای مغناطیسی را در جهت مثبت ایجاد می‌کند. اگر این شتاب در جهت عکس باشد، گردابه مغناطیسی نیز در جهت منفی خواهد بود.
• مغناطیس: شکل‌های مختلفی از امواج گردابی در مغناطیس‌ها نیز وجود دارند. این گردابه‌ها پاسخ‌های دقیق معادلاتِ کلاسیک غیر خطی‌ای همچون معادله «لاندو لیفشیتز» (Landau-Lifshitz)، مدل پیوسته هایزنبرگ و «معادله ایشیموری» (Ishimori Equation) هستند.
• حلقه‌های دود: یک حلقه دود که برای مدت زمانی اندک به صورت پایدار حرکت می‌کند، در حقیقت گردابه‌ای است که انرژی آن توسط ویسکوزیته سیال دفع می‌شود.
• گردباد: گردباد، ورتکسی قدرتمند محسوب شده که مشخصه‌ آن شکلی قیف گونه از توده‌ جویِ در حال چرخش است. به چنین گردبادی که روی سطح آب ایجاد می‌شود، «پیچند دریایی» (Waterspout) گفته می‌شود.
• طوفان: این نمونه از گردابه نسبت به گردباد بسیار قدرتمندتر بوده و هم‌چون گردباد به صورت قیفی شکل است. طوفان در نتیجه بخار شدن آب اقیانوس‌ها و چرخش زمین ایجاد می‌شود. در دیگر سیاره‌ها طوفان می‌تواند بسیار بزرگ‌تر نیز باشد. برای نمونه چشم سرخ قرار گرفته روی مشتری، طوفانی دائمی محسوب می‌شود که اندازه آن تقریبا به اندازه زمین است. البته در دیگر سیاره‌ها همچون نپتون نیز چنین چشمی وجود دارد.
• گردابه قطبی: در نزدیکی دو قطب زمین گردابه‌ای جوی و چرخان وجود دارد که در بالای تروپوسفر قرار گرفته است. این ناحیه کم فشار بوده و وجود آن به منظور ایجاد جریان همرفتی در زمین ضروری است. در زمستان، گردابه قطب شمال رشد کرده و منجر به فرستادن توده‌ای از جریان سرد به سمت جنوب می‌شود.
• لکه خورشیدی: ناحیه‌ای روی سطح خورشید که نسبت به اطرافش از دمای کمتری برخوردار بوده، بنابراین به رنگ مشکی دیده می‌شود. هم‌چنین این ناحیه به صورت دائم دارای میدان مغناطیسی شدیدی است.
• سیاهچاله: در سیاهچاله یا نواحی از کیهان که گرانش شدید باشد، اجرام موجود در فضا به صورتی شتاب دار و دایره‌ای به مرکز جرم نزدیک می‌شوند. این حرکت دیسکی چرخان را ایجاد می‌کند که نوعی گردابه محسوب می‌شود.

ویژگی‌های گردابه

گردابه‌ها ناحیه‌هایی خاص محسوب شده و تحت شرایطی ویژه تشکیل می‌شوند. از این رو ویژگی‌های این ناحیه نیز نسبت به دیگر نواحی متفاوت است.

• فشار سیال در مرکز یک گردابه کمترین مقدار را دارد. این در حالی است که سرعت در مرکز آن ماکزیمم است. در حالی که از مرکز فاصله می‌گیریم فشار افزایش یافته و سرعت کاهش می‌یابد. رابطه بین افزایش و کاهش این کمیت‌ها را می‌توان با استفاده از معادله برنولی توصیف کرد.
• معمولا می‌توان مرکز یک ورتکس را به صورت مجزا از دیگر نواحی جدا کرد. دلیل این امر وجود ناحیه کم‌فشار در مرکز است. در این ناحیه به علت فشار اندک، بخار آب جدا شده و تصویر آن مجزا می‌شود.
• مرکز هر گردابه را می‌توان با استفاده از خطی تحت عنوان خط ورتکس به صورت مجزا تشخیص داد. در حقیقت هر ذره‌ای در ورتکس حول خط ورتکس در حال دوران است. خط ورتکس می‌تواند از ابتدا تا انتهای سیال ادامه دار بوده یا تشکیل یک حلقه بسته را بدهد. توجه داشته باشید که گردابه‌ها همواره به نحوی منحرف می‌شوند که به سطح جامد متصل شوند. برای نمونه معمولا روی صفحات کمپرسور موتور‌های جت گردابه تشکیل می‌شود. هنگامی که هواپیما روی زمین در حال حرکت است یک سمت از گردابه به موتور متصل بوده و سمت دیگر آن به زمین اتصال دارد. گردابه ایجاد شده می‌تواند سنگ و یا دیگر اشیاء کوچک را به درون موتور هدایت کند.

• توجه داشته باشید که قدرت یک گردابه با استفاده از عددی تحت عنوان «گردش» (Circulation) اندازه‌گیری می‌شود. اگر دو یا چند ورتکس با گردش‌های متفاوت به صورت موازی با یکدیگر در حال چرخش باشند، در این صورت تمایل آن‌ها به منظور یکپارچه شدن و تشکیل یک گردابه واحد وجود دارد. در این حالت گردشِ گردابه تشکیل شده برابر با حاصل جمع گردشِ هریک از گردابه‌ها است. برای نمونه مجموعه‌ای از ورتکس‌های کوچک در لبه انتهایی ایرفویل یا پره هواپیما تشکیل می‌شوند. معمولا این ورتکس‌ها در هنگام تولید نیروی برا (لیفت) در ایرفویل یا تولید پیشرانش در پره‌ها ایجاد می‌شوند. در چنین شرایطی در فاصله‌ای کمتر از طول یک «کورد» (Chord) در پشت ایرفویل این مجموعه گردابه‌‌ها یکپارچه شده و تشکیل یک گردابه واحد را می‌دهند.
  اگر از پشت به یک هواپیما، در جهت پرواز نگاه کنیم، یک گردابه ساعتگرد روی بال سمت چپ و گردابه‌ای پادساعتگرد روی بال سمت راست ایجاد می‌شود. در تصویر زیر این گردابه نشان داده شده است. توجه داشته باشید که این دو ورتکس با هم یکپارچه نخواهند شد چرا که جهت دوران آن‌ها عکس یکدیگر است.

دینامیک گردابه

در مکانیک سیالات، قدرت دوران یک ورتکس را با استفاده از کمیتی تحت عنوان «چرخش» (Vorticity) اندازه‌گیری می‌کنند. به طور دقیق‌تر می‌توان گفت این کمیت متناسب با نسبت گردش به سطح، در یک نقطه خاص از گردابه در نظر گرفته می‌شود. چرخش کمیتی برداری بوده که جهت آن در جهت محور گردابه است.

در علم هواشناسی، ورتکس کمیتی است که معادل با چرخش توده‌های جرمی عظیم در نظر گرفته می‌شود. از آنجایی که چرخش توده‌های جوی تقریبا افقی هستند، بنابراین جهت بردار چرخش آن‌‌ها نیز به صورت عمودی است. از این رو در محاسبات می‌توان از یک عدد استفاده کرد. از نظر ریاضیاتی بردار چرخشِ $$\overrightarrow {\omega}$$ برابر است با:

$$\large \overrightarrow {\omega} = \nabla × \overrightarrow {u}$$

در رابطه فوق $$\large \overrightarrow {u}$$ نشان دهنده میدان سرعت است. بنابراین در ابتدا فرض کنید که میدان سرعت یک جریان به صورت زیر باشد.

$$\large \overrightarrow{ V } = v _ x \overrightarrow { i } + v _ y\overrightarrow { j } + v _ z \overrightarrow { k }$$

در این صورت چرخش برابر است با:

$$\large {\displaystyle {\begin{aligned}{\overrightarrow {\omega }}=\nabla \times {\overrightarrow {v } } &={\begin{pmatrix}{\frac {\partial }{\partial x} } , \large {\frac {\partial }{\partial y}} , {\frac {\partial } { \partial z } } \end {pmatrix} } \times {\begin{pmatrix} v _ { x }, v _ { y } , v _ { z } \end{pmatrix}} \\ \large &={\begin{pmatrix}{\frac { \partial v _ { z } } { \partial y } } - { \frac {\partial v _ { y } } { \partial z } } , { \frac { \partial v _ { x } } { \partial z } } – { \frac {\partial v_{z}}{\partial x } },{ \frac { \partial v _ { y } } { \partial x } } – { \frac {\partial v _ { x } } { \partial y } } \end {pmatrix} } \, \end{aligned} } }$$

همان‌طور که در رابطه فوق نیز می‌بینید بردار چرخش دارای سه مولفه است. بنابراین شکل کلی این بردار به صورت $$\overrightarrow {\omega} = (\omega _ x \ , \ \omega _ y \ , \omega _ z \ )$$ خواهد بود.

انواع ورتکس

البته مدل‌های مختلفی از ورتکس در طبیعت وجود دارد. با این حال دو نوع از معروف‌ترین آن‌ها که بیشتر مورد بررسی قرار می‌گیرند، ورتکس‌های چرخشی (Rotational) و غیرچرخشی (Irrotational) هستند.

ورتکس‌ غیرچرخشی

جریانی که به درون سینک ریخته می‌شود را می‌توان با دقت قابل قبولی به صورت غیرچرخشی در نظر گرفت. در این نوع از ورتکس سرعت مماسی متناسب با $$\frac { 1 } { r }$$ تغییر می‌کند. از این رو اندازه تکانه زاویه‌ای نیز ثابت است. ثابت بودن تکانه‌ زاویه‌ای به معنای آن است که چرخشِ ورتکس غیرچرخشی برابر با صفر است ($$\overrightarrow { \omega } =0$$). در این حالت سرعت مماسی برابر است با:

$$\large v _ { \theta } = \frac { \Gamma } { 2 \pi r } \,$$

فیلم مجموعه آموزش مهندسی مکانیک – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

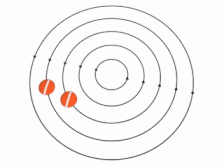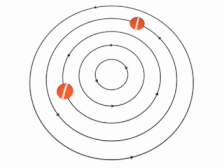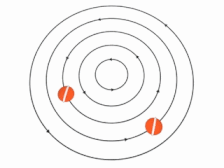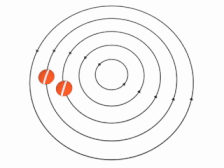
در رابطه فوق $$\Gamma$$ نشان دهنده گردش و $$r$$ نشان دهنده فاصله از مرکز دوران است. در انیمیشن زیر نحوه حرکت ذرات یک جریان غیرچرخشی نشان داده شده است.

توجه داشته باشید که واژه چرخشی یا غیرچرخشی به المان‌های سیال اشاره دارد. در انیمیشن زیر نحوه حرکت ذرات یک جریان غیرچرخشی نشان داده شده. همان‌طور که می‌بینید با چرخش کل سیال، المان‌های آن دوران نمی‌کنند. در حقیقت خط سفید‌رنگِ قرار گرفته وسط ذره با گذشت زمان دوران نمی‌کند.

جریان چرخشی (ورتکس اجباری)

در جریان چرخشی یا ورتکس اجباری، جریان همچون جسمی صلب دوران می‌کند. در این حالت اثرات ویسکوزیته و تنش برشی در جریان نیز در نظر گرفته می‌شود. اگر فرض بر این باشد که کل سیال همچون جسمی جامد با سرعت زاویه‌ای $$\omega$$ در حال دوران باشد، در این صورت اندازه چرخش سیال برابر با $$2 \omega$$ خواهد بود. به منظور شبیه‌سازی چنین ورتکسی می‌توانید ظرفی از آب را در نظر بگیرید که سرعت زاویه‌ای آن به آرامی افزایش یافته تا به مقدار $$\omega$$ برسد. در این صورت ظرف به همراه آب درون آن با سرعت $$\omega$$ دوران خواهد کرد. توجه داشته باشید که در این حالت سرعت خطی نیز همچون حرکت دایره‌ای به صورت زیر محاسبه می‌شود.

$$ \large v _ { \theta } = \omega r \ $$

انیمیشن زیر نحوه حرکت ذرات در یک جریان چرخشی را نشان می‌دهد.

بر خلاف جریان غیرچرخشی در این حالت ذرات با گذشت زمان حول محور خودشان نیز دوران می‌کنند. در ادامه نحوه حرکت این ذرات نشان داده شده است.

^^