معادله انرژی در ترمودینامیک – از صفر تا صد
پیش از این در مجله فرادرس، جنبههای مختلف علم ترمودینامیک را بررسی کردیم. فرآیندهای آیزنتروپیک و آدیاباتیک را معرفی کردیم. نقطه سهگانه و نمودار فازی را مورد مطالعه قرار دادیم و در مقالهای دیگر نیز به جمعبندی صفر تا صد این شاخه از مهندسی مکانیک پرداختیم. در مقاله حاضر، معادله انرژی را در ترمودینامیک تشریح خواهیم کرد. یکی از بنیادیترین قوانین طبیعت، قانون اول ترمودینامیک است که تحت عنوان قضیه پایستگی انرژی هم شناخته میشود. این قانون، روابط بین شکلهای مختلف انرژی و برهمکنش میان آنها را مطالعه میکند. براساس قانون اول ترمودینامیک، «در یک فرآیند، انرژی نه به وجود میآید و نه از بین میرود؛ تنها از حالتی به حالتی دیگر تبدیل میشود.»
مقدار انرژی در یک سیستم بسته را میتوان به دو روش تغییر داد: یکی انتقال گرما $$\large Q$$ و دیگری انجام کار $$\large W$$. در نتیجه، معادله انرژی برای چنین سیستمی، به صورت زیر نوشته میشود.
$$\large \dot{Q} - \dot{W} \: = \frac {dE_{sys}} {dt} , ~~~ \dot{Q} - \dot{W} \: = \frac {d} {dt} {\int_{sys}} \rho e \:d\nu \\ ~ \\
\large \dot{Q} = \dot {Q}_{net, \: in} \: =\dot{Q}_{in} \: - \dot {Q}_{out} \\ ~ \\
\large \dot{W} = \dot {W}_{net, \: out} \: =\dot{W}_{out} \: - \dot {W}_{in}$$
در رابطه بالا، $$\large \dot {Q}_{net, \: in}$$ نرخ انتقال خالص گرما به سیستم است. توان خالص خروجی را نیز با $$\large \dot {W}_{net, \: out}$$ نشان دادهایم و عبارت $$\large \frac {dE_{sys}} {dt}$$ بیان کننده نرخ تغییرات در انرژی کل سیستم است. برای سیستمهای تراکمپذیر ساده، انرژی کل، شامل انرژیهای درونی، جنبشی و پتانسیل میشود. انرژی کل را در جرم واحد و به شکل زیر تعریف میکنیم.
$$\large e = u + ke + pe = u + \frac {V^2} {2} + gz$$
مقدار انرژی کل فقط در صورتی تغییر میکند که حالت سیستم عوض شود. گرما، به شکلی از انرژی گفته میشود که نیروی محرکه آن، اختلاف دما است. کار نیز شکل دیگری از انرژی است که در هنگام اعمال نیرویی در حین یک جابجایی، تعریف میشود. کار میتواند به شکلهای مختلفی در یک سیستم ظاهر شود. در این صورت، کار کل برابر با مجموع این کارها خواهد بود.
$$\large W_ {total} = W_ {shaft} + W_ {pressure} + W_ {viscous} + W_ {other}$$
کار منتقل شده توسط محور چرخان، با $$W_ {shaft}$$ نشان داده میشود. $$W_ {pressure}$$ برابر با کار انجام شده توسط نیروهای فشار روی سطح کنترل است. کار انجام شده توسط مؤلفههای عمودی و برشی نیروهای ویسکوز را با $$W_ {viscous}$$ تعریف کردهایم و $$W_ {other}$$، کار انجام شده توسط سایر نیروها مانند تنشهای سطحی، نیروهای الکتریکی و نیروهای مغناطیسی را نشان میدهد. معمولاً در سیستمهای تراکمپذیر ساده، میتوان از این نیروها چشم پوشید. از طرف دیگر، معمولاً نمونه سؤالات امتحانی دانشگاهها طوری طراحی میشود که در آنها، کار نیروی ویسکوز در مقابل سایر مقادیر کار، به قدری کوچک است که نیازی به محاسبه آن وجود ندارد. البته باید به خاطر داشت که برای نوشتن معادله انرژی در مسائل توربوماشین، کار انجام شده توسط نیروهای برشی که پرههای توربین به سیال وارد میکنند، باید در نظر گرفته شود.
تأثیر فشار در معادله انرژی
شکل زیر را در نظر بگیرید. گاز داخل سیلندر، در حال فشرده شدن است. هنگامی که پیستون به اندازه $$\large ds$$ پایین میآید، کار مرزی انجام شده روی سیستم برابر $$\large \delta W _ {boundary} = PA \: d s$$ است. با تقسیم دو طرف این رابطه به $$\large dt$$، نرخ کار مرزی انجام شده (توان) به دست میآید.
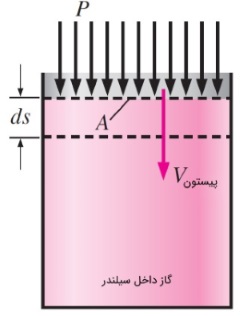
$$\large \delta \dot{W}_ {pressure} = \dot{W} _ {boundary} = PAV_{piston} $$
در رابطه بالا، $$\large V_{piston} = ds/dt$$ سرعت پیستون را نشان میدهد که در واقع همان سرعت جابجایی مرزی است. حال، بخش جدا شدهای از یک سیستم سیال را با شکل دلخواه در نظر بگیرید. همانطور که میبینید، این بخش با جریان سیال، حرکت میکند و میتواند تحت تأثیر فشار، آزادانه تغییر شکل دهد. فشار همیشه به سمت داخل و عمود بر سطح عمل میکند. نیروی حاصل از فشار روی سطح جزئی $$\large dA$$ را با $$\large PdA$$ نشان میدهیم. میدانیم که کار برابر با حاصل ضرب نیرو در جابجایی و سرعت نیز برابر جابجایی در واحد زمان است. نرخ زمانی کار انجام شده توسط نیروهای فشار روی این جزء دیفرانسیلی از سیستم، برابر با عبارت زیر نوشته میشود. زیرا مؤلفه عمودی سرعت در سطح دیفرانسیلی $$\large dA$$ برابر با $$\large V_n = V \: \cos \theta \: = \: \overrightarrow{V} . \overrightarrow{n}$$ است.
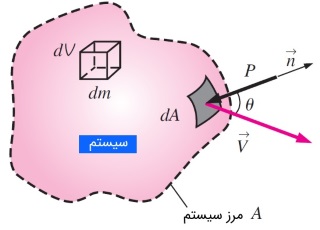
$$\large \delta \dot{W}_{pressure} = P \: dA \: V_n \: = \: P \: dA \: (\overrightarrow{V} . \overrightarrow{n})$$
با توجه به جهت بردار $$\large \overrightarrow{n}$$ بدیهی است که علامت $$\large \overrightarrow{V} . \overrightarrow{n}$$ در هنگام انبساط، مثبت و در هنگام تراکم، منفی است. توان خالص حاصل از نیروهای فشار را میتوان با محاسبه انتگرال از جزء $$\large \delta \dot{W} _ {pressure}$$ در کل سطح $$\large A$$ به دست آورد.
$$\large \dot{W} _ {pressure, \: net \: out} = \int _{A} P(\overrightarrow{V}.\overrightarrow{n}) \:dA = \int_{A} \frac {P}{\rho} \rho(\overrightarrow{V}.\overrightarrow{n}) dA$$
(رابطه ۱)
حال میتوانیم توان خالص خروجی را سادهتر از قبل بنویسیم.
$$\large \dot{W}_{net, \: out} = \dot{W} _ {shaft, \: net \: out} + \int _{A} P(\overrightarrow{V}.\overrightarrow{n}) \:dA $$
همچنین میتوانیم معادله انرژی را برای یک سیستم بسته به شکل زیر بیان کنیم.
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} - \dot{W} _ {pressure, \: net \: out} = \frac {dE_{sys}} {dt}$$
اکنون برای یافتن رابطهای برای پایستگی انرژی در یک حجم کنترل، از قضیه انتقال رینولدز استفاده میکنیم. این قضیه در کتابهای مکانیک سیالات برای حجمهای کنترل اثبات شده است. بازنویسی این قضیه برحسب مقادیر انرژی کل $$\large E$$ و انرژی واحد جرم $$\large e$$، به رابطه زیر منجر میشود.
$$\large \frac {dE_{sys}} {dt} = \frac {d} {dt} \int _{CV} e\rho \: d\nu + \int _ {CS} e \rho (\overrightarrow{V}_r . \overrightarrow{n}) \:dA$$
اکنون با مقایسه دو رابطه اخیر، معادله انرژی را به شکل زیر نتیجه میگیریم.
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} - \dot{W} _ {pressure, \: net \: out} = \frac {d} {dt} \int _{CV} e\rho \: d\nu + \int _ {CS} e \rho (\overrightarrow{V}_r . \overrightarrow{n}) \:dA$$
(رابطه ۲)
در واقع میتوان این رابطه را به این صورت تفسیر کرد؛ نرخ کل انرژیهایی که به شکل کار و گرما به حجم کنترل منتقل شدهاند با مجموع نرخ تغییرات انرژی در حجم کنترل و نرخ انتقال انرژی به بیرون از سطح کنترل برابر است. در اینجا، $$\large \overrightarrow{V}_r = \overrightarrow{V} - \overrightarrow{V}_{CS}$$ سرعت سیال را نسبت به سطح کنترل نشان میدهد و عبارت $$\large \rho (\overrightarrow{V}_r . \overrightarrow{n}) \:dA$$ نیز بیان کننده نرخ دبی جرمی از سطح دیفرانسیلی $$\large dA$$ به داخل یا خارج از حجم کنترل است. جهت بردار $$\large \overrightarrow{n}$$ به سمت بیرون $$\large dA$$ است. در نتیجه برای دبی جرمی خارج شونده، علامت $$\large \overrightarrow{V}_r . \overrightarrow{n}$$ مثبت و برای دبی جرمی وارد شونده، علامت آن منفی خواهد بود. حال با مقایسه رابطههای شماره ۱ و ۲، معادله انرژی به صورت رابطه زیر نوشته میشود.
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} = \frac {d} {dt} \int _{CV} e\rho \: d\nu + \int _ {CS} (\frac {P} {\rho} + e) \rho (\overrightarrow{V}_r . \overrightarrow{n}) \:dA$$
در رابطه بالا، کار ناشی از فشار با انرژی سیالی که از سطح کنترل عبور میکند ادغام شده و دیگر نیازی به محاسبه جداگانه کار ناشی از فشار نیست. عبارت $$\large P/ \rho = P \nu = w_{flow}$$ کار جریان نامیده میشود و برابر با کار ناشی از هُل دادن سیال به داخل یا بیرون از حجم کنترل در واحد جرم است. به این نکته دقت کنید که سرعت سیال در یک سطح صلب با سرعت آن سطح صلب برابر است. زیرا این حرکت بدون لغزش در نظر گرفته میشود و در سطوحی که حرکت ندارند، این سرعت مساوی صفر است. بنابراین، کار فشار در بخشی از سطح کنترل که با سطوح صلب ساکن در تماس است، صفر خواهد بود. در نتیجه، در یک حجم کنترل ساکن، فقط در قسمتی موهومی از سطح کنترل، که سیال وارد حجم کنترل شده و از آن خارج میشود، کار فشار وجود دارد.
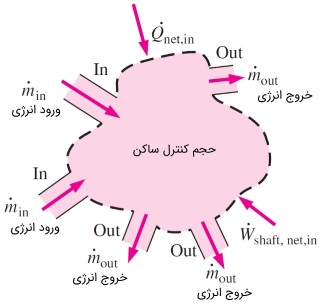
با این حال، معادلهای که به دست آوردیم، به دلیل داشتن انتگرال، هنوز برای حل مسائل واقعی مهندسی مناسب نیست. پس بهتر است با کمک مقادیر متوسط سرعت و دبی جرمی در ورودی و خروجی سطح کنترل، آن را بازنویسی کنیم. به شکل بالا توجه کنید. در مسائل مهندسی، حجم کنترل دارای تعداد زیادی ورودی و خروجی است. در این حالت، انرژی میتواند از هر ورودی داخل و از هر خروجی خارج شود. از طرف دیگر، انتقال حرارت و کار محوری هم راههای دیگری برای انتقال انرژی هستند. اگر عبارت $$\large P/ \rho + e$$ در ورودی و خروجی تقریباً یکنواخت باشد، میتوانیم آن را از زیر انتگرال خارج کنیم. همانطور که میدانیم، نرخ دبی جرمی در ورودی یا خروجی با استفاده از رابطه $$\large \dot{m} = \int _{A_c} \rho (\overrightarrow{V}_r . \overrightarrow{n}) \:dA_c$$ به دست میآید و نرخ ورود و خروج انرژی نیز تقریباً برابر $$\large \dot{m} (P / \rho \:+ e)$$ است. در این حالت، معادله انرژی به شکل زیر خواهد بود.
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} = \frac {d} {dt} \int _{CV} e\rho \: d\nu \: + \sum_{out} \dot{m} (\frac {P} {\rho} + e) \: - \sum_{in} \dot{m} (\frac {P} {\rho} + e)$$
در رابطه بالا، $$\large e$$ انرژی کل در واحد جرم است و برای حجم کنترل و جریان سیال به صورت $$\large e \: =u \: + \frac {V^2} {2} \: + gz$$ تعریف میشود. بنابراین، معادله انرژی را میتوانیم به یکی از دو شکل زیر بیان کنیم.
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} = \frac {d} {dt} \int _{CV} e\rho \: d\nu \: + \sum_{out} \dot{m} (\frac {P} {\rho} + u + \frac {V^2} {2} + gz) \\~\\
\large - \sum_{in} \dot{m} (\frac {P} {\rho} + u + \frac {V^2} {2} + gz)$$
(رابطه ۳)
$$\large \dot {Q} _ {net, \: in} - \dot{W} _ {shaft, \: net \: out} = \frac {d} {dt} \int _{CV} e\rho \: d\nu \: + \sum_{out} \dot{m} (h + \frac {V^2} {2} + gz) \\~\\
\large - \sum_{in} \dot{m} (h + \frac {V^2} {2} + gz)$$
(رابطه ۴)
در رابطههای بالا از تعریف آنتالپی $$\large h = u + P\nu = u + P/ \rho$$ استفاده شده است. دو رابطه آخر، بیان کلی قانون پایستگی انرژی هستند ولی استفاده از آنها محدود به جریان یکنواخت در ورودی و خروجی و ناچیز بودن نیروهای ویسکوز است.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مکانیک
- مجموعه آموزشهای دروس مهندسی مکانیک
- عدد ماخ — به زبان ساده
- ترمودینامیک — از صفر تا صد
- سرعت صوت — از صفر تا صد
- جریان تراکم پذیر (Compressible Flow) — اصول و مفاهیم
^^










سایتتون خرابه خداوکیلی حروف قاطی شده درست نمیشه درستش کنین خداوکیلی