تصاعد هندسی و فرمول آن — به زبان ساده و با مثال

دنباله و سری‌ها، شاید در اول به عنوان سرگرمی‌های ریاضی شناخته می‌شدند ولی یکی از ابزارهای مهم در توصیف پدیده‌ها نیز هستند. بسیاری از محاسبات بدون آگاهی نسبت به رفتار دنباله‌ها، میسر نبود. یکی از دنباله‌های پرکاربرد، تصاعد هندسی است. در این متن می‌خواهیم شما را با تصاعد هندسی و فرمول آن آشنا کنیم تا به این ترتیب بتوانید رابطه یا جمله عمومی چنین دنباله‌ای را بنویسید. پدیده‌های زیادی مانند تکثیر سلول‌ها، میزان افزایش اپیدمی و ... از الگوها یا تصاعدهای هندسی پیروی می‌کنند. در این بین از ذکر مثال‌هایی برای روشن‌تر شدن موضوع استفاده خواهیم کرد. رسم نمودارهای مرتبط با تصاعدها و همچنین مجموع آن‌ها در این نوشتار از مجله فرادرس مورد توجه قرار گرفته است.

در نوشتار دنباله هندسی و مجموع آن — به زبان ساده و سری همگرا و واگرا — از صفر تا صد با دنباله‌ها و شرط همگرایی آن‌ها آشنا شده‌اید. همچنین قواعد مربوط به سری توانی در مجله فرادرس به زبان ساده، شرح داده شده ولی در این متن قرار است دنباله هندسی و فرمول آن را مورد بررسی قرار داده و جمله عمومی و مجموع تصاعد هندسی یا سری هندسی را مشخص کنیم.

تصاعد هندسی

«دنباله» (Sequence) یا «تصاعد» (Progression) یک اصطلاح ریاضی است که برای نمایش ارتباط بین اعداد به کار می‌رود. اعدادی که در یک تصاعد یا دنباله ظاهر می‌شوند دارای ترتیب بوده و نظم خاصی دارند.

فیلم آموزش ریاضی پایه دانشگاهی در فرادرس

کلیک کنید

یک دنباله را به صورت پارامتری به شکل $$\{x_n\}_{n = 1}^N$$ نشان می‌دهند. البته در این جا فرض کرده‌ایم که دنباله متناهی است و اندیس آن نیز با $$n$$ مشخص شده. آخرین اندیس یا شماره جمله هم با $$N$$ در رابطه قبل دیده می‌شود.

برای مثال یک دنباله حسابی را که برای نمایش اعداد زوج به کار می‌رود، به صورت زیر نشان می‌دهیم.

$$\large {\displaystyle x_1 = 2, \ x_2 = 4, \ x_3 = 6, \ldots } $$

از آنجایی که بی‌نهایت عدد زوج وجود دارد، در انتهای اعداد این دنباله از $$\ldots$$ استفاده کردیم که به معنی «ادامه دارد» است. بیان ریاضی این دنباله به صورت زیر خواهد بود.

$$\large {\displaystyle \{ x_n \}_{n = 1 }^{ \infty} ,\ x_n = 2 \times n  , \ n \in ℕ} $$

که در آن $$\mathcal{ℕ}$$ همان مجموعه اعداد طبیعی است. البته می‌توانیم این دنباله را به صورت ارتباط بین جمله‌ها نیز بنویسیم.

$$\large {\displaystyle \{ x_n \}_{ n = 1 }^{ \infty} ,\ x_{ n + 1} = x_n + 2 } $$

همانطور که در فرمول بالا می‌بینید، هر جمله از تصاعد حسابی، با مقدار ثابتی جمع شده و جمله بعدی از تصاعد را ساخته است. ولی در تصاعد هندسی، به جای جمع از ضرب جملات در یک مقدار ثابت استفاده می‌شود. دنباله هندسی زیر را در نظر بگیرید.

6 , 30, 150, 750, 3750 , ...

هر جمله از این دنباله، مضربی از جمله اول یعنی ۶ هستند. بهتر است هر جمله را بر جمله اول یعنی شش تقسیم کنیم و نتیجه را مورد تحلیل قرار دهیم.

$$\large {\displaystyle \dfrac{ 30}{ 6} = 5, \ \dfrac{ 150}{ 6} = 25, \dfrac{ 750}{ 6} = 125 , \dfrac{ 3750}{ 6} = 625 } $$

اگر به نتیجه تقسیم‌ها توجه کنید، مشخص است که همه آن‌ها، توان‌هایی از ۵ هستند. بنابراین رابطه بالا را به صورت زیر بازنویسی می‌کنیم.

$$\large {\displaystyle \dfrac{ 30}{ 6} = 5, \ \dfrac{ 150}{ 6} = 5^2, \dfrac{ 750}{ 6} = 5^3, \dfrac{ 3750}{ 6} = 5^4} $$

طبق رابطه بالا، اگر هر جمله از تصاعد هندسی را بر جمله قبلی تقسیم کنیم، خارج قسمت برابر با ۵ خواهد شد.

$$\large {\displaystyle \dfrac{ 30}{ 6} = 5, \ \dfrac{ 150}{ 30} = 5, \dfrac{ 750}{ 150} = 5, \dfrac{ 3750}{ 750} = 5} $$

این خارج قسمت را در تصاعد هندسی، قدر نسبت یا نسبت مشترک می‌گویند.

تصاعد هندسی و فرمول آن

اگر در یک «تصاعد هندسی» (Geometric Progression)، جمله اول و مقدار قدر نسبت مشخص باشد، می‌توانیم همه جمله‌های این تصاعد را مشخص کنیم. رابطه‌ای که برای انجام این کار لازم است به صورت زیر نوشته می‌شود. فرض کنید جمله اول به صورت $$a$$ و مقدار قدر نسبت دنباله هندسی با حرف $$r$$، مشخص باشد.

$$ \large {\displaystyle a , \ a\ r, \ a\ r^2, \ a\ r^3, \ \ldots, \quad \quad r \neq 0 }$$

رابطه ۱: جملات یک دنباله یا تصاعد هندسی

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

بنابراین جمله عمومی یک تصاعد هندسی که با نماد $$x_n$$ به کار می‌رود، طبق رابطه زیر بدست می‌آید. البته توجه دارید که اندیس $$n$$ باید بزرگتر از ۱ باشد. در حقیقت $$n$$ مکان عدد مورد نظر در دنباله هندسی را مشخص می‌کند.

$$ \large {\displaystyle x_n = a \ r^{( n -1)} , \; n \geq 1} $$

رابطه ۲: جمله عمومی تصاعد هندسی

البته می‌توان جمله عمومی را برحسب جمله قبلی آن نیز نوشت. رابطه ۳ چنین حالتی را برای بیان تصاعد هندسی مشخص کرده است.

$$ \large {\displaystyle x_n = r \ x_{ n-1} , \; n \geq 1} $$

رابطه ۳: جمله عمومی تصاعد هندسی

مثال ۱: دنباله هندسی با جمله اول ۲ و قدر نسبت ۴ را تشکیل دهید و چهار جمله اول آن را مشخص کنید.

واضح است که در اینجا $$a = 2$$ و $$r = 4 $$ است. پس جمله عمومی برابر است با:

$$ \large {\displaystyle x_n = 2 \times 4^{(n -1)} , \; n \geq 1} $$

به این ترتیب چهار جمله اول آن به صورت زیر نوشته خواهد شد. البته مشخص است که این دنباله، نامتناهی است و تا بی‌نهایت ادامه خواهد داشت.

$$ \large {\displaystyle  2 , \ 8, \ 32, \  128, \ldots } $$

با توجه به ترتیبی که در دنباله یا تصاعد هندسی بالا وجود دارد، مشخص است که هر عدد از عدد قبلی خود، بزرگتر است. در چنین حالتی، تصاعد هندسی را صعودی می‌نامند. به نمودار مربوط به این تصاعد که در ادامه قابل مشاهده است، نگاه کنید. روند صعودی در این دنباله از اعداد به خوبی مشخص است.

مثال ۲: یک دنباله هندسی با جمله اول $$a = 5$$ و قدر نسبت $$r = \frac{1}{2}$$ تشکیل دهید.

با توجه به رابطه ۲، جمله عمومی را می‌نویسیم.

$$ \large {\displaystyle x_n = 5 \ (\dfrac{ 1}{ 2})r^{ (n -1)} , \; n \geq 1} $$

در نتیجه جمله‌های آن به صورت زیر در می‌آید.

$$ \large {\displaystyle  5 , \ \dfrac{ 5}{ 2}, \  \dfrac{ 5}{ 4}, \ \dfrac{5}{ 16} , \ldots } $$

به یاد داشته باشید که برای جمله اول، $$n = 1$$‌ است. همچنین برای جمله دوم و سوم و الی آخر، مقدار $$n$$ را یک واحد، یک واحد، افزایش می‌دهیم. همانطور که مشاهده می‌کنید، هر جمله این تصاعد از جمله قبلی خود کوچکتر است. چنین دنباله‌ای را نزولی می‌نامیم. در نمودار زیر، تغییرات این تصاعد را مشاهده می‌کنید. به راحتی می‌توانید چنین نموداری را با اکسل ترسیم کنید.

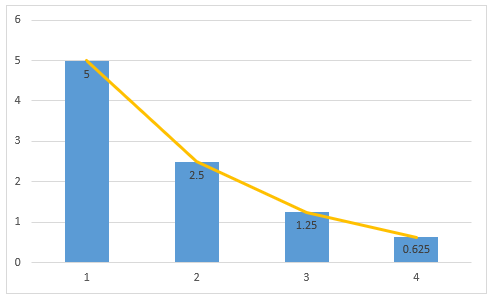
نکته: به کمک این مثال می‌توان نتیجه گرفت، اگر قدر نسبت یک تصاعد هندسی، در بازه $$(0,1)$$ قرار گیرد، دنباله نزولی خواهد بود. زیرا ضرب هر عدد در عددی کوچکتر از ۱ و مثبت، آن را کاهش می‌دهد. ولی اگر قدر نسبت، مقداری منفی باشد، چه اتفاقی خواهد افتاد.

مثال 3: دنباله هندسی با جمله اول ۱ و قدر نسبت 0٫5- را تشکیل دهید و چهار جمله اول آن را مشخص کنید.

باز هم مشخص است که $$a = 1$$ و $$r = -0.5 $$ است. پس جمله عمومی برابر است با:

$$ \large {\displaystyle x_n = 1 \times (- 0.5)^{(n -1)} , \; n \geq 1} $$

از آنجایی که قدر نسبت در این تصاعد، منفی است، جمله‌های یک در میان مثبت و منفی خواهند شد. به این ترتیب چهار جمله اول را به صورت زیر محاسبه می‌کنیم. البته مشخص است که این دنباله، نامتناهی است و تا بی‌نهایت ادامه خواهد داشت.

1, -0٫5, 0٫25, -0٫125, 0٫0625, ...

می‌بینید که قدر مطلق چنین دنباله‌ای، یک دنباله نزولی ساخته است. حاصل قدر مطلق این دنباله در زیر نوشته شده است.

1, |-0٫5|, 0٫25, |-0٫125|, 0٫0625, ... → 1, 0٫5, 0٫25, 0٫125, 0٫0625, ...

ولی اگر بدون تابع قدر مطلق، چنین تصاعدی را در نظر بگیریم، وضعیت نزولی و صعودی مشخصی ندارد و یک بر نزولی و بار بعدی صعودی خواهد بود. به تصویر زیر که دنباله مربوط به مثال اصلی را نمایش داده، توجه کنید.

به کمک مثال‌های بالا، به طور کلی در مورد قدر نسبت و همچنین نزولی یا صعودی بودن دنباله‌های هندسی می‌توان از گزاره‌های زیر استفاده کرد.

• اگر قدر نسبت یک تصاعد هندسی، مقداری مثبت باشد، همه جمله‌های تصاعد، هم علامت با جمله اول هستند.
• با منفی بودن مقدار قدر نسبت در یک تصاعد هندسی، جمله‌ها، یک در میان مثبت و منفی خواهند شد. به عبارت دیگر اگر جمله اول مثبت باشد، جمله دوم منفی، جمله سوم مثبت، جمله چهارم منفی و ... خواهد بود.
• مقدار قدر نسبت در تصاعد هندسی نباید برابر با ۱ باشد، در غیر اینصورت، تصاعدی به وجود نیامده و همه جمله‌ها، با یکدیگر برابر می‌شوند.
• مقدارهای بزرگتر از ۱ برای قدر نسبت در تصاعد هندسی، باعث بوجود آمدن دنباله صعودی شده و به مانند یک تابع نمایی رشد می‌کنند.
• مقدارهای بین صفر و ۱، باعث ایجاد یک دنباله یا تصاعد هندسی نزولی خواهند شد.
• مقدارهای منفی بین صفر و ۱-، دنباله‌ای متناوب با قدر مطلق نزولی خواهند ساخت.
• مقدارهای کوچکتر از ۱- برای قدر نسبت، یک دنباله متناوب ولی با قدر مطلق صعودی ایجاد می‌کنند.

همانطور که در این لیست خواندید، اگر قدر نسبت برابر با صفر، ۱ یا ۱- باشد، دنباله یا تصاعد هندسی شکل نخواهد گرفت. در تصویر زیر یک نمونه از تصاعد هندسی نزولی را مشاهده می‌کنید که با قدر نسبت ۱/۲ ساخته شده است. واضح است که جمله اول برای این تصاعد ۱ خواهد بود. شکل نمایش این تصاعد بسیار به شکل دنباله فیبوناچی شبیه است.

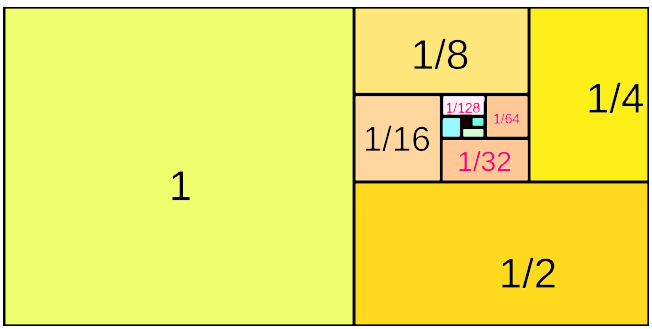
همانطور که در این تصویر می‌بینید، بزرگترین مربع، با مساحت ۱ در نظر گرفته شده، مربع یا مستطیل بعدی، نصف مربع اولی، مساحت دارد. به همین ترتیب هر بار مساحت شکل بعدی، نصف مساحت شکل قبلی است. با تکرار این تقسیم‌بندی، شکل‌ها و در نتیجه مساحتشان کوچکتر و کوچکتر می‌شود. به نظر می‌رسد که این دنباله یا تصاعد هندسی، به صفر همگرا است. یعنی جملات انتهایی دنباله، به مقدار صفر میل می‌کند.

واسطه هندسی و ویژگی جالب در تصاعد هندسی

فرض کنید که سه جمله متوالی از یک دنباله یا تصاعد هندسی در اختیار شما است. آن‌ها را به ترتیب $$a, b , c$$ می‌نامیم تا راحت‌تر محاسبات را دنبال کنیم. واضح است که اگر تصاعد، صعودی باشد رابطه $$a \leq b \leq c$$ برقرار است. در حالتی که تصاعد نزولی باشد، رابطه برعکس شده و به شکل $$c \leq b \leq a$$ نوشته می‌شود. در حالت متناوب نیز نمی‌توانیم رابطه ترتیبی قطعی مشخص کنیم. ولی به هر حال برای قدر مطلق آن یکی از دو حالت قبلی رخ خواهد داد.

فیلم آموزش ریاضی و آمار ۳ – پایه دوازدهم علوم انسانی در فرادرس

کلیک کنید

از طرفی براساس رابطه ۱ و ۲ می‌توانیم $$b$$ را برحسب $$a$$ و $$c$$ بنویسیم.

$$ \large {\displaystyle b = r a}$$

$$ \large {\displaystyle b = c / r }$$

حال طرف راست این تساوی‌ها را در هم و طرف چپ را هم در هم ضرب می‌کنیم. رابطه زیر بین سه جمله متوالی از تصاعد هندسی مشخص می‌شود که آن را واسطه هندسی می‌نامند.

$$ \large {\displaystyle b^2 = c \times a}$$

رابطه ۴: واسطه هندسی و رابطه بین جملات متوالی در تصاعد هندسی

مثال 4: فرض کنید سه جمله متوالی از یک تصاعد هندسی به صورت $$3 , x , 27$$ است. مقدار $$x$$ را تعیین می‌کنیم. به فرمول زیر توجه کنید که در آن از رابطه ۴ استفاده شده است.

$$ \large {\displaystyle b^2 = c \times a \xrightarrow{ a = 3 , \ x = b,\ c = 27} x^2 =  3 \times 27 = 81 \rightarrow x = \pm\ 9 }$$

از آنجایی که قدر نسبت دقیقا مشخص نیست، می‌توان هر دو مقدار ۹ و ۹- را به عنوان جمله وسط در نظر گرفت. می‌دانید که اگر قدر نسبت در این تصاعد، مثبت باشد، مقدار ۹ و اگر قدر نسبت منفی باشد، مقدار ۹- به عنوان جمله وسط تصاعد هندسی منظور می‌شود.

این بار همین مثال را به شکل دیگری در نظر می‌گیریم که در آن دنباله به صورت $$x , -9 , 27$$ است. باز هم از رابطه ۴ کمک می‌گیریم.

$$ \large {\displaystyle b^2 = c \times a \xrightarrow{ a = x , \ b = -9,\ c = 27} (-9)^2 = 81 =  x \times 27 \rightarrow x = \dfrac{ 81}{ 27}  \rightarrow x = 3 }$$

مجموع جملات تصاعد هندسی و فرمول آن

این بار، مجموع جمله‌های یک تصاعد که یک سری محسوب می‌شود، را مورد بررسی قرار می‌دهیم. به یاد داشته باشید، چون رابطه بین هر یک از جمله‌ها در تصاعد هندسی، ضربی است و مقدار ثابتی در هر جمله ضرب شده، تصاعد را هندسی می‌نامند. از این جهت، این مجموع نیز سری هندسی نامیده می‌شود.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال 5: دنباله‌ای حاصل از توان‌های عدد 2 را در نظر بگیرید. این اعداد و مجموعشان را در رابطه زیر مشاهده می‌کنید.

$$ \large {\displaystyle 2 + 4 + 8 + 16 + 32 + 64 = 126}$$

اگر بتوانیم برای مجموع چنین اعدادی، یک قاعده یا الگو مشخص کنیم، امکان جمع‌ کردن آن‌ها برای تعداد جمله‌های بیشتر نیز بوجود می‌آید و می‌توانیم به کمک آن الگو حتی جمع بی‌نهایت جمله از تصاعد هندسی را بدست آوریم.

مثال 6: به عنوان یک مثال دیگر مجموع اعداد کسری زیر را در نظر بگیرید.

$$ \large {\displaystyle \dfrac { 1}{ 2}} \, + \, { \dfrac { 1}{ 4}} \, + \,{ \dfrac { 1}{ 8}} \, + \,{ \dfrac { 1}{ 16}}$$

همانطور که می‌بینید، این جمله‌ها به ترتیب (از بزرگ به کوچک) نوشته شده و با یکدیگر جمع شده‌اند. به نظر شما رابطه بین این جمله‌ها چیست؟ بله درست است، هر جمله نصف جمله قبلی است.

اگر بخواهیم این جمله‌ها را با یکدیگر جمع کنیم، با استفاده از مخرج مشترک، کسرها را با مخرج یکسان نوشته و صورت‌ کسرهای جدید را با هم جمع می‌کنیم.

$$ \large {\displaystyle \dfrac { 1}{ 2}} \, + \, { \dfrac { 1}{ 4}} \, + \,{ \dfrac { 1}{ 8}} \, + \,{ \dfrac { 1}{ 16} = \dfrac { 8}{ 16}} \, + \, { \dfrac { 4}{ 16}} \, + \,{ \dfrac { 2}{ 16}} \, + \,{ \dfrac { 1}{ 16} = \dfrac{ 8 + 4 + 2 + 1 }{ 16} = \dfrac{ 15}{ 16} }$$

همانطور که می‌بینید، این کار ساده نبود و اگر تعداد جمله‌های این الگو بیشتر شوند، به سختی می‌توانیم مجموع اعداد آن که سری را مشخص می‌کنند، بدست آوریم. توجه داشته باشید، زمانی که از یک سری صحبت می‌کنیم، منظورمان مجموع مقادیر یک الگو یا دنباله است.

سری هندسی و جمع متناهی جملات دنباله هندسی

دنباله هندسی زیر را با جمله اول $$a$$ و قدر نسبت $$r$$ در نظر بگیرید.

$$ \large {\displaystyle a , \ a\ r, \ a\ r^2, \ a\ r^3, \ \ldots \quad \quad ; r \neq 0 }$$

در این صورت مجموع این جمله‌ها را تا جمله $$n$$ام، به صورت زیر نمایش می‌دهیم.

$$ \large {\displaystyle \sum _{i = 0}^{ n} a r^{ i} = a r^{ 0} + a r^{1} + a r^{ 2} + a r^{ 3} + \ldots + a r^{ n}\,} $$

می‌خواهیم برای این حاصل جمع، یک رابطه یا فرمول بدست آوریم تا بدون آنکه جمع را انجام دهیم، حاصل با بدانیم. چنین رابطه‌ای به صورت زیر است.

$$ \large {\displaystyle \sum_{i = 0}^{ n} a r^{ i}={ \dfrac {a ( 1 - r^{n + 1})}{ 1- r}}} $$

رابطه 5: مجموع جملات یک تصاعد هندسی و فرمول آن

مثال 7: با استفاده از فرمول گفته شده، مجموع جملات تصاعد هندسی مربوط به مثال 5 را بدست می‌آوریم. جمله اول برابر با ۲ و قدر نسبت هم برابر با ۲ است.

$$ \large {\displaystyle \sum_{i = 0}^{ n} 2 \times 2^{ i}={ \dfrac { 2 ( 1 - 2^{n + 1})}{ 1- 2}}= 2^{n + 2} - 2 } $$

که اگر مقدار $$n=5$$ در نظر گرفته شود،‌ حاصل جمع برابر است با $$2^ 7 - 2  = 128 - 2 = 126$$ که با مقدار محاسبه شده در مثال 5، مطابقت دارد.

مثال 8: این بار به سراغ مثال 6 می‌رویم و مجموع جملات آن تصاعد هندسی را پیدا می‌کنیم. توجه دارید که جمله اول $$\frac{ 1}{ 2}$$ و قدر نسبت هم $$\frac{ 1}{ 2}$$ است.

$$ \large {\displaystyle \sum_{i = 0}^{ n} \dfrac{ 1}{ 2} (\dfrac{ 1}{ 2})^{ i}={ \dfrac { \dfrac{ 1}{ 2} ( 1 - (\dfrac{ 1}{ 2})^{ n + 1})}{ 1- \dfrac{ 1}{ 2}}}} $$

که به شکل زیر ساده می‌شود.

$$ \large {\displaystyle \sum_{i = 0}^{ n} \dfrac{ 1}{ 2} (\dfrac{ 1}{ 2})^{ i }= 1- (\dfrac{ 1}{ 2})^{ n + 1 }} $$

به این ترتیب مجموع این دنباله برای چهار جمله اول ($$n = 3$$) به صورت زیر درخواهد آمد.

$$ \large {\displaystyle \sum_{i = 0}^{ 3} \dfrac{ 1}{ 2} (\dfrac{ 1}{ 2})^{ i} =1-  (\dfrac{ 1}{ 2})^{3 + 1}= 1- \dfrac{ 1}{ 2^4} = 1- \dfrac{ 1}{ 16} = \dfrac{ 15}{ 16} } $$

نکته: توجه دارید که در اینجا وقتی $$n=3$$ باشد و مقدار $$i$$ از صفر آغاز شود، چهار جمله پدید خواهد آمد. که در نتیجه فرمول هم برای جمع چهار جمله مشخص خواهد شد.  به همین علت برای جمع چهار جمله اول، مقدار $$n$$ را عدد ۳ در نظر گرفتیم.

جمع نامتناهی جملات دنباله هندسی

در این بخش به بررسی جمع در یک دنباله نامتناهی از تصاعد هندسی می‌پردازیم. به بیان دیگر، یک تصاعد هندسی در اختیار داریم که تعداد بی‌شمار جمله دارد و می‌خواهیم در صورت همگرایی دنباله، جمع آن را محاسبه کنیم. در صورتی که دنباله همگرا نباشد، جمع نامتناهی آن وجود ندارد.

در قسمت‌های قبلی مشخص کردیم که اگر مقدار قدر نسبت در یک تصاعد هندسی مثبت و بزرگتر از ۱ باشد، دنباله صعودی است. پس نمی‌توان همگرایی را برای چنین دنباله‌ای نشان داد. در اغلب موارد، زمانی که $$0<r <1$$، همگرایی وجود دارد. البته در زمانی که مقدار قدر نسبت، منفی باشد، باز هم می‌توان همگرایی را تحقیق کرد. ولی به دلیل سادگی، در ادامه این متن، فقط حالتی را مورد بررسی قرار می‌دهیم که در آن $$r$$ مثبت و بین صفر و یک قرار داشته باشد.

محاسبه جمع نامتناهی جملات دنباله هندسی طبق رابطه زیر صورت می‌گیرد.

$$ \large {\displaystyle \sum_{ i = 0}^{ \infty } a r^{i}= {\dfrac {a}{ 1 - r}} , \ 0 < r < 1 }$$

رابطه 6: جمع نامتناهی جملات دنباله هندسی

البته از رابطه بالا برای زمانی که مقدار قدر نسبت در بازه $$-1 < r <0$$ قرار داشته باشد نیز می‌توان استفاده کرد. با مقایسه رابطه ۶ و ۵ می‌بینیم که عبارت $$r^n$$ از بین رفته است. همانطور که می‌دانید، زمانی که عددی در بازه $$(0,1)$$ قرار داشته باشد، توان‌های صحیح مثبت آن، کوچک و کوچک‌تر می‌شوند و در نهایت به صفر میل خواهند کرد. به همین جهت اگر در رابطه ۵، مقدار $$r^n$$ را زمانی که $$n$$ خیلی بزرگ است، محاسبه کنیم، نزدیک به صفر خواهد بود و بهتر است از آن چشم پوشی کرده تا به رابطه ۶ برسیم.

مثال ۹: فرض کنید مجموع اعداد کسری مربوط به مثال ۶، تا بی‌نهایت ادامه داشته باشد. در حقیقت دنباله یا تصاعد هندسی مورد نظر به صورت زیر است.

$$\large {\displaystyle \dfrac { 1}{ 2}} \, , \, { \dfrac { 1}{ 4}} \, , \,{ \dfrac { 1}{ 8}} \, , \,{ \dfrac { 1}{ 16} \ , \ \ldots } $$

با توجه به این قدر نسبت در این تصاعد، برابر با $$\frac{1}{2}$$ است، می‌توان همگرایی را نتیجه گرفت و مجموع نامتناهی این جملات را بدست آورد. از فرمول یا رابطه 6 استفاده کرده و مقدار $$a = \frac{1}{2}$$ و $$r = \frac{1}{2}$$ را به کار می‌بریم.

$$ \large {\displaystyle \sum_{ i = 0}^{ \infty } \dfrac{ 1}{ 2} \times \dfrac{ 1}{ 2}^{i}= {\dfrac { 1}{ 2} \times \dfrac{ 1 }{ 1- \dfrac{ 1 }{ 2} }} = \dfrac{ 1}{ 2} \times 2 = 1 }$$

همانطور که مشاهده می‌کنید، طبق فرمول ارائه شده، این سری هندسی به مقدار ۱ همگرا است.

مثال ۱۰: این بار مقدار قدر نسبت را منفی ولی بزرگتر از ۱- در نظر گرفته و مجموع یک تصاعد هندسی را بدست می‌آوریم. مثال ۳ را در نظر بگیرید. قدر نسبت در این تصاعد هندسی برابر با ۰٫۵- یا $$\frac{ -1 }{ 2}$$ است و جمله اول هم برابر با ۱ است. به این ترتیب می‌توان نتیجه گرفت که مجموع نامتناهی آن یعنی سری هندسی حاصل، همگرا است و می‌توان نقطه همگرایی را مشخص کرد.

واضح است که این تصاعد، متناوب است، یعنی جمله‌های آن یک درمیان مثبت و منفی هستند ولی از طرفی همگرا محسوب می‌شود. مجموع نامتناهی از جملات این تصاعد به صورت زیر در خواهد آمد.

$$
\large {\displaystyle \sum_{ i = 0}^{ \infty } 1 \times (\dfrac{ -1}{ 2})^{ i}= { \dfrac{ 1 }{ 1 - ( - \frac{ 1 }{ 2} ) }}} = \frac { 2 } { 3 }
$$

پس مجموع این تصاعد هندسی منتاوب به سمت دو سوم میل می‌کند یا همگرا به دو سوم است.

خلاصه و جمع‌بندی

بسیاری از پدیده‌های فیزیکی یا شیمایی، از تصاعد یا دنباله‌ها پیروی می‌کنند. تصاعد حسابی و تصاعد هندسی و فرمول های مربوطه، برای شناخت چنین پدیده‌هایی که توسط دنباله‌ای از نشان داده می‌شوند، مهم و ضروری هستند زیرا در اکثر مواقع، با چنین تصاعدهایی سروکار داریم. به همین منظور در این متن به بررسی تصاعد هندسی پرداختیم و به کمک چند مثال و رسم نمودارهایی، درک بهتری نسبت به آن‌ها بدست آوردیم. واسطه هندسی یا رابطه بین سه جمله متوالی از تصاعد هندسی نیز از مواردی بود که این دنباله را جذاب می‌کند. با ذکر دو مثال، واسطه هندسی را هم به کار گرفته و رابطه بین جمله‌ها را مشخص کردیم.

البته در بخشی از متن به مجموع جملات تصاعد هندسی چه در حالت متناهی و چه نامتناهی پرداختیم و فرمول و رابطه‌های محاسبه این مجموع را بیان کردیم. همانطور که خواندید، شرط همگرایی یک دنباله یا تصاعد هندسی براساس قدر نسبت آن مشخص می‌شود که در صورت قرارگیری آن در بازه ۱- تا ۱ (به جز صفر)، سری هندسی، همگرا خواهد بود.