تبدیل فوریه گسسته — از صفر تا صد

در آموزشهای پیشین مجله فرادرس، با تبدیل فوریه و ویژگیهای آن آشنا شدیم. تبدیل فوریه گسسته یکی از ابزارهای قدرتمند در پردازش سیگنال دیجیتال است که با استفاده از آن میتوان طیف سیگنالی با طول متناهی را به دست آورد. در این آموزش، با تبدیل فوریه گسسته آشنا میشویم.
مواقع و شرایط زیادی وجود دارد که نیاز داریم محتوای فرکانسی یک سیگنال حوزه زمان را مشخص کنیم. برای مثال، ممکن است بخواهیم طیف خروجی یک نوسانساز LC را برای مشاهده مقدار نویز موجود در سیگنال سینوسی تولیدی تحلیل کنیم. این کار با استفاده از تبدیل فوریه گسسته (Discrete Fourier Transform) یا DFT میسر است. تبدیل فوریه گسسته، در کنار فیلترسازی دیجیتال، یکی از دو ابزار قوی پردازش سیگنال دیجیتال است.
تبدیل فوریه گسسته چیست؟
سیگنال پیوسته را در نظر بگیرید که در شکل ۱ نشان داده شده است.
میخواهیم این سیگنال را تحلیل کنیم.
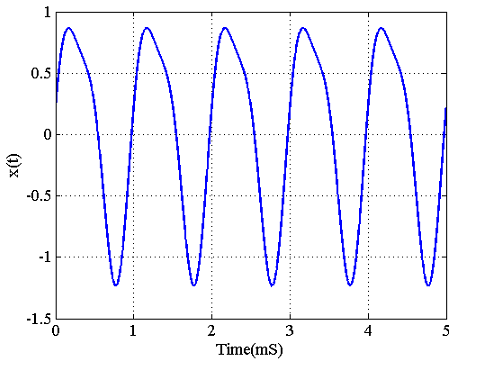
بدیهی است که یک کامپیوتر دیجیتال نمیتواند با یک سیگنال پیوسته کار کند و لازم است که تعدادی نمونه از بگیریم و به جای سیگنال اصلی، این نمونهها را تحلیل کنیم. علاوه بر این، علیرغم اینکه شکل ۱ تنها ۵ میلیثانیه از سیگنال را نشان میدهد، ممکن است ساعتها، سالها یا بیشتر از آن ادامه داشته باشد. از آنجایی که کامپیوتر دیجیتال توانایی فقط تعداد محدودی از نمونهها را دارد، باید از تقریب استفاده کرده و از تعداد محدودی نمونه بهره ببریم. بنابراین، عموماً، دنبالهای به طول محدود برای نمایش این سیگنال پیوسته آنالوگ به کار میرود که میتواند روی محور زمان به مثبت بینهایت میل کند. از سیگنال شکل ۱ با نرخ نمونهبرداری ۸۰۰۰ نمونه بر ثانیه، تعداد نمونه میگیریم. نتیجه این نمونهبرداری در شکل ۲ نشان داده شده است.
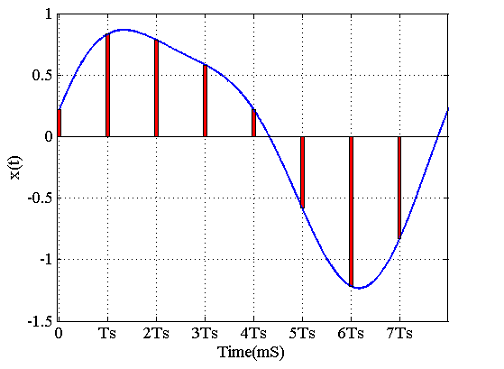
اگر محور زمان را به دوره نمونهبرداری بهنجار (نرمالیزه) کنیم، دنباله گسسته را به دست خواهیم آورد که در جدول زیر ارائه شده است:
تحلیل فوریه چندین ابزار ریاضی را برای تعیین محتوای فرکانسی یک سیگنال حوزه زمان ارائه میکند، اما کدامیک از این ابزارها برای تحلیل مناسبتر است؟ تنها دو روش از خانواده تحلیل فوریه وجود دارد که مختص سیگنالهای گسستهاند: تبدیل فوریه زمانگسسته (Discrete-time Fourier Transform) یا DTFT و تبدیل فوریه گسسته (Discrete Fourier Transform) یا DFT.
تبدیل فوریه زمانگسسته (DTFT) دنباله ورودی به صورت زیر بیان میشود:
معکوس DTFT نیز به شکل زیر است:
میتوانیم از معادله (۱) برای یافتن طیف سیگنال استفاده کنیم که دامنه زمانی آن متناهی است. در معادله بالا، تابعی پیوسته از است. بنابراین، یک کمپیوتر دیجیتال نمیتواند مستقیماً از معادله (۱) برای تحلیل استفاده کند. البته میتوانیم از نمونههای برای یافتن تقریبی از طیف استفاده کنیم. ایده نمونهبرداری در نقاط فرکانسی با فاصله برابر، در واقع، اساس روش دوم فوریه، یعنی DFT است که در بالا به آن اشاره کردیم. توجه کنید که این نمونهبرداری در حوزه فرکانس انجام میشود ( تابعی از فرکانس است).
ریاضیات تبدیل فوریه گسسته (DFT)
این بخش را با بررسی مثالی که در بخش قبل بیان کردیم معرفی میکنیم. دنبالهای به طول از سیگنال داریم که مربوط سیگنال پیوسته آنالوگ است. هدفی که به دنبال آن هستیم، یافتن مجموعهای از سینوسیها است که میتوان آنها را با هم جمع و را تولید کرد.
همانطور که در بخش قبلی گفتیم، DFT مبتنی بر نمونهبرداری در نقاط فرکانسی با فواصل برابر از DTFT است که در رابطه (۱) داده شد. یک تابع دورهای یا متناوب از با دوره تناوب است. اگر در هر دوره ، تعداد نمونه بگیریم، فاصله بین نقاط نمونهبردای خواهد بود. بنابراین، فرکانس مجموعه سینوسیهایی که به دنبال یافتن آنها هستیم، به فرم خواهد بود که در آن، . با استفاده از نماییهای مختلط مشابه با معادلات (۱) و (۲)، توابع پایه به صورت خواهند بود. میخواهیم یک مجموع وزندار از این توابع را پیدا کنیم که سیگنال اصلی را نتیجه دهند. در نتیجه، خواهیم داشت:
که در آن، وزن نمایی مختلط است. معادله (۳)، معادل با مجموعه معادلات زیر است:
برای یک و مشخص، مقادیر نماییهای مختلط معلوم بوده و با داشتن مقدار سیگنال حوزه زمان میتوانیم ضرایب را محاسبه کنیم. تعداد نمونههای حوزه زمان ()، تعداد معادلات را در مجموعه معادلات و تعداد نمونههای حوزه فرکانس ، تعداد مجهولات معادله (۴) را مشخص میکند. با قرار دادن ، تعداد معادله مستقل خطی برای یافتن مجهولِ خواهیم داشت.
با فرض ، میتوانیم فرم ماتریسی معادله (۴) را نوشته و با استفاده از متلب، مجهولات را به دست آوریم:
اما تفسیر این تحلیل چیست؟ ما دنباله را به صورت مجموع نماییهای مختلط معادله (۳) نوشتیم. اکنون نتایج را در معادله مذکور جایگذاری میکنیم. با و حذف نماییهایی که ضریبشان صفر است، طبق جدول بالا میتوان نوشت:
از آنجایی که این توابع نمایی دورهای با هستند، میتوانیم این معادله را سادهتر کنیم. برای مثال، برابر با است. بعد از سادهسازی و بازآرایی جملات معادله بالا، خواهیم داشت:
در نهایت، رابطه زیر را به دست خواهیم آورد:
رابطه بالا نشان میدهد که میتوانیم را با دو مؤلفه نشان دهیم: یکی در فرکانس نرمالیزه با دامنه و دیگری در با دامنه . این فرکانسها نرمالیزه هستند؛ اگر فرکانس نمونهبرداری نمونه بر ثانیه باشد، فرکانس این دو مؤلفه، به ترتیب، و خواهد بود.
اکنون خلاصهای را از آنچه که گفتیم بیان میکنیم. ما با یک سیگنال زمانپیوسته شروع کردیم و از تعداد محدودی نمونه برای تحلیل محتوای فرکانسی این سیگنال پیوسته استفاده کردیم. دیدیم که مسئله تجزیه این دنباله گسسته به حل مجموعهای از معادلات خطی میانجامد. در مثال سادهای که بررسی کردیم، معادله (۵) را نیز ساده کرده و یک معادله صریح برای به دست آوردیم.
این، نکتهای است که باید توجه ویژهای به آن داشته باشیم. تحلیل با دنبالهای به طول ۸ شروع میشود که در شکل ۳ نشان داده شده است. واضح است که مقدار را برای میدانیم، اما اطلاعی از مقدار آن در خارج از این محدوده نداریم.
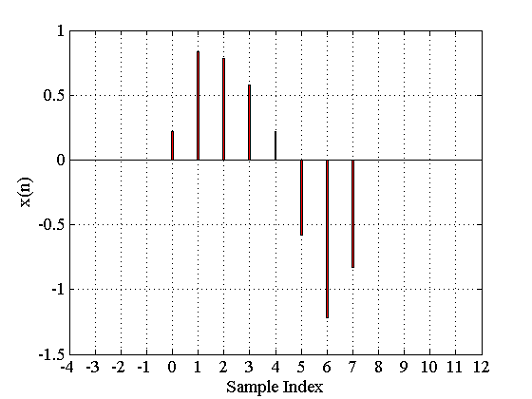
تحلیل بالا، در واقع، جستوجو برای مجموعی از نماییهای مختلط است که میتوانند مقادیر را برای بازتولید کنند. معادله (۵) را در خارج از این بازه آزمایش میکنیم. برای جلوگیری از ابهام، به دنباله بر میگردیم که در معادله (۵) داده شد. نمودار که یک تابع دورهای با است، در شکل ۴ نشان داده شده است. همانطور که در این شکل میبینیم، مقادیر اصلی هر ۸ نمونه یکبار تکرار میشوند. به عبارت دیگر، وقتی بتوانیم را با استفاده از تعدادی نمایی مختلط نشان دهیم، نمایشِ به دست آمده متناوب بوده و فقط در یک دوره تناوب برابر با است.
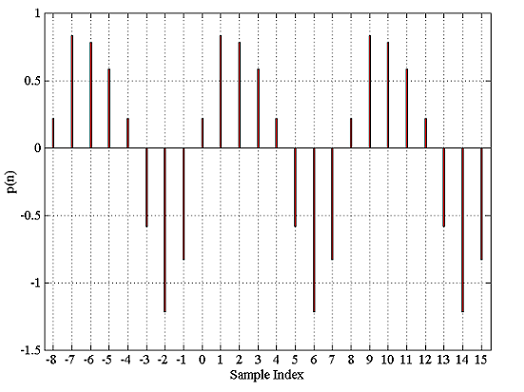 میشود که فرم متناوب است." width="524" height="392">
میشود که فرم متناوب است." width="524" height="392">توجه کنید که وقتی درباره تشکیل، تحلیل و اعمال DFT بحث میکنیم، منظورمان نمایشی از دنبالهای با طول متناهی با استفاده از یک دنباله متناوب است که در آن، مقادیرِ یک دوره تناوب از این دنباله دورهای برابر با مقادیر آن دنباله متناهی هستند.
همچنین دقت داشته باشید که رفتار دورهای را میتوان با یادآوری این نکته درک کرد که در حال نمونهبرداری از در حوزه فرکانس (تبدیل فوریه زمانگسسته ) هستیم. در واقع، نمونهبرداری از در حوزه فرکانس، به نسخه برابر در حوزه زمان میانجامد. فرم تناوبی در شکل ۳ و در شکل ۴ نشان داده شد.
استخراج معادلات DFT
روش بالا را که برای محاسبه طیف یک دنباله با طول متناهی بیان کردیم، ساده و قابل درک است و مبیّن رفتار تناوبی ذاتی نمایش DFT است. با وجود این، میتوانیم از مباحث بالا استفاده کرده و فرم بسته معادلات DFT را بدون نیاز به محاسبه معکوس یک ماتریس بزرگ به دست آوریم. برای این کار، تنها لازم است یک سیگنال تناوبی با نمونه از دنبالهای با طول متناهی بسازیم. پس از آن، با اعمال بسط سری فوریه زمانگسسته، میتوانیم نمایش حوزه فرکانس سیگنال تناوبی را به دست آوریم. ضرایب سری فوریه به دست آمده، جز برای یک عامل مقایسبندی، مشابه ضرایب DFT هستند.
فرض کنید دنباله متناهی که میخواهیم آن را تحلیل کنیم در شکل ۵ (الف) نشان داده شده است. برای محاسبه تبدیل فوریه گسسته Nنقطهای، لازم است از روی سیگنال با دوره تناوب ، سیگنال را بسازیم (شکل ۵ (ب)).
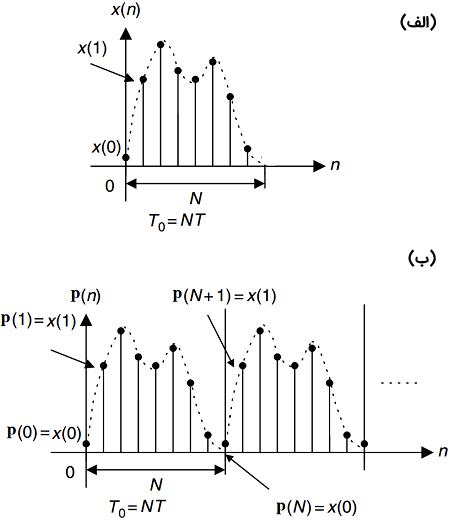 که میخواهیم آن را تحلیل کنیم. (ب) سیگنال متناوب به دست آمده از " width="449" height="523">
که میخواهیم آن را تحلیل کنیم. (ب) سیگنال متناوب به دست آمده از " width="449" height="523">با توجه به رابطه به ازای سری فوریه زمانگسسته این سیگنال متناوب به صورت زیر است:
که در آن، دوره تناوب سیگنال است. سیگنال حوزه زمان را میتوان به صورت زیر به دست آورد:
با ضرب ضرایب معادله (۶) در ، ضرایب تبدیل فوریه گسسته () به دست میآید:
تبدیل فوریه گسسته معکوس به صورت زیر خواهد بود:
توجه کنید که وقتی سری فوریه زمانگسسته یک سیگنال متناوب باشد، ضرایب DFT یک دنباله متناهی در هستند.
مثالها
در این بخش، دو مثال ساده را بررسی میکنیم.
مثال ۱
فرض کنید ، . تبدیل فوریه گسسته به صورت زیر است:
بنابراین، به صورت زیر خواهد بود:
توجه کنید که وقتی ، و وقتی ، داریم:
مثال ۲
تبدیل فوریه را به دست آورید.
حل: در این مثال، داریم:
بنابراین، میتوان گفت: ، ، و . در نتیجه، پاسخ است.
در نتیجه، به صورت زیر خواهد بود:
با تبدیل ضرایب مختلط به نماییهای مختلط، داریم:
این مثال، موردی از جابهجایی فاز است که اتفاق میافتد. با در نظر گرفتن بخشهای حقیقی هر دو سمت، مجموعی از موجهای کسینوسی خواهیم داشت:
که در آن، افزوده شدن ، و موجب جابهجایی شکل موجها به ترتیب، به اندازه ، و خواهد شد.
تعامد و تبدیل معکوس
چرا فرمول تبدیل معکوس درست است؟ را در فرمول جایگذاری میکنیم:
اگر ، مجموع داخلی طبق فرمول سری هندسی برابر با صفر است. وقتی ، مجموع داخلی برابر با خواهد بود. بنابراین، مجموع کلی برابر است با .
یک راه دیگر برای بررسی این استدلال، آن است که این امر نتیجه تعامد نسبت به ضرب نقطهای مختلط است. بردارهای مختلط زیر را در نظر بگیرید:
که در آنها، است. با استدلالی مشابه آنچه در بالا گفتیم، این بردارهای مختلط نسبت به ضرب نقطهای مختلط متعامد هستند: اگر و در غیر این صورت، برابر با صفر است.
فرمول DFT برای به سادگی به صورت بیان میشود، که در آن، بردار است. فرمول معکوس، را با نوشتن با استفاده از فرمول استاندارد برای بیان هر بردار به عنوان ترکیب خطی بردارهای پایه متعامد بر حسب بر میگرداند:
پیادهسازی تبدیل فوریه گسسته
در این بخش، مراحل پیادهسازی الگوریتم تبدیل فوریه گسسته را بیان کرده و آن را در زبانهای برنامهنویسی مختلف ارائه میکنیم.
در حالت کلی میتوان گفت که DFT تابعی است که برداری با عدد مختلط را به برداری با عدد مختلط دیگر مینگارد. با در نظر گرفتن مبداء ، فرض میکنیم نشان دهنده اُمین درایه بردار ورودی و نشان دهنده اُمین درایه بردار خروجی باشد. تبدیل فوریه گسسته پایه با فرمول زیر بیان میشود:
فرمول بالا مبیّن این موضوع است که بردار سطح یا اندازه سیگنال را در نقاط زمانی مختلف نشان میدهد و بردار مجموع اندازه را در فرکانسهای مختلف به نمایش میگذارد. آنچه این فرمول میگوید، این است که اندازه سیگنال در فرکانس برابر است با مجموع اندازههای سیگنال در هر زمان ضرب در یک نمایی مختلط.
با داشتن دانش کمی درباه نماد مجموع، اعداد مختلط و برنامهنویسی کامپیوتری میتوانیم به سادگی برنامه تبدیل فوریه گسسته را بنویسیم. در ادامه، این فرایند را گام به گام بررسی میکنیم. برای نمونه، این مراحل را در قالب زبان برنامهنویسی جاوا بیان خواهیم کرد.
ساختار برنامه
همانطور که گفتیم، سری فوریه گسسته یک بردار با عدد مختلط را به عنوان ورودی میگیرد و بردار خروجی را که شامل عدد مختلط است محاسبه میکند. از آنجایی که جاوا عدد مختلط ندارد، باید خودمان عدد مختلط را با استفاده از دو عدد حقیقی تعریف کنیم. بردار، دنبالهای از اعداد است که میتوان آن را با یک آرایه نمایش داد. به جای بازگرداندن آرایههای خروجی، آنها را به عنوان آرگومان در مرجع قرار خواهیم داد. ساختار آن به صورت زیر است:
1void dft(double[] inreal , double[] inimag,
2 double[] outreal, double[] outimag) {
3 // Assume all 4 arrays have the same length
4 int n = inreal.length;
5 // Incomplete: Method body
6}در ادامه حلقه بیرونی را برای اختصاص دادن یک مقدار به هر درایه خروجی مینویسیم:
1void dft(double[] inreal , double[] inimag,
2 double[] outreal, double[] outimag) {
3 int n = inreal.length;
4 for (int k = 0; k < n; k++) { // For each output element
5 outreal[k] = ?; // Incomplete
6 outimag[k] = ?; // Incomplete
7 }
8}مجموع
نوشتن مجموع یا همان سری شاید در ابتدا کمی پیچیده به نظر برسد، اما در واقع برعکس است. فرم کلی یک مجموع به صورت زیر ساده میشود:
در حقیقت، در سری بالا مقادیر را یک به یک جایگذاری میکنیم. به سادگی کد سری بالا را میتوان به صورت زیر نوشت:
1double sum = 0;
2for (int j = a; j <= b; j++) {
3 sum += f(j);
4}
5// The value of 'sum' now has the desired answerریاضیات عدد مختلط
جمغ دو عدد مختلط به سادگی انجام میشود:
ضرب دو عدد مختلط کمی سختتر است؛ با استفاده از قانون توزیع و اتحاد ، داریم:
طبق رابطه اویلر، برای هر عدد حقیقی ، میتوان تساوی را نوشت. علاوه بر این، کسینوس یک تابع زوج بوده و رابطه برقرار است. همچنین، از آنجایی که سینوس یک تابع فرد است، میتوان تساوی را نوشت. بنابراین، خواهیم داشت:
نماد را به عنوان بخش حقیقی و را به عنوان بخش موهومی آن در نظر میگیریم. طبق تعریف، . بنابراین:
با گسترش ضرب مختلط، داریم:
بنابراین، هر عبارت در مجموع کد زیر را برای بخشهای حقیقی و موهومی خواهد داشت:
1double angle = 2 * Math.PI * t * k / n;
2double real = inreal[t] * Math.cos(angle) + inimag[t] * Math.sin(angle);
3double imag = -inreal[t] * Math.sin(angle) + inimag[t] * Math.cos(angle);ترکیب همه بخشها با یکدیگر
اگر همه بخشها را که گفتیم، با هم ترکیب کنیم، برنامه زیر را برای محاسبه سری فوریه گسسته خواهیم داشت:
1static void dft(double[] inreal , double[] inimag,
2 double[] outreal, double[] outimag) {
3 int n = inreal.length;
4 for (int k = 0; k < n; k++) { // For each output element
5 double sumreal = 0;
6 double sumimag = 0;
7 for (int t = 0; t < n; t++) { // For each input element
8 double angle = 2 * Math.PI * t * k / n;
9 sumreal += inreal[t] * Math.cos(angle) + inimag[t] * Math.sin(angle);
10 sumimag += -inreal[t] * Math.sin(angle) + inimag[t] * Math.cos(angle);
11 }
12 outreal[k] = sumreal;
13 outimag[k] = sumimag;
14 }
15}در ادامه، کد DFT را برای چند زبان برنامهنویسی مختلف ارائه میکنیم. قبل از بررسی این کدها، نکات زیر را در نظر داشته باشید:
- زبانهای برنامهنویسی پایتون، سی، سیپلاسپلاس، سیشارپ، و متلب، اعداد مختلط را به صورت توکار دارند. این ویژگی کارمان را برای نوشتن برنامه DFT بسیار آسانتر میکند.
- هریک از برنامهها، نامگذاری قراردادی، سبک قالببندی و اصطلاحات کدنویسی مربوط به خود را دارند و لزوماً شبیه آن چیزی نیستند که برای جاوا بیان کردیم.
- تبدیل فوریه گسستهای که در این بخش بیان کردیم، برای سادگی، شامل نرمالیزه کردن/مقیاسبندی نیست. گزینههای متعددی برای چگونگی مقیاسبندی DFT وجود دارد. مثلاً مقیاسبندی فقط تبدیل مستقیم با ، مقیاسبندی تبدیلهای مستقیم و معکوس با ، مقیاسبندی جداول مثلثاتی از پیش محاسبه شده و... .
برنامه تبدیل فوریه گسسته در جاوا
1/*
2 * Discrete Fourier transform (Java)
3 * by Project Nayuki, 2017. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7
8public final class Dft {
9
10 /*
11 * Computes the discrete Fourier transform (DFT) of the given complex vector.
12 * All the array arguments must be non-null and have the same length.
13 */
14 public static void computeDft(double[] inreal, double[] inimag, double[] outreal, double[] outimag) {
15 int n = inreal.length;
16 for (int k = 0; k < n; k++) { // For each output element
17 double sumreal = 0;
18 double sumimag = 0;
19 for (int t = 0; t < n; t++) { // For each input element
20 double angle = 2 * Math.PI * t * k / n;
21 sumreal += inreal[t] * Math.cos(angle) + inimag[t] * Math.sin(angle);
22 sumimag += -inreal[t] * Math.sin(angle) + inimag[t] * Math.cos(angle);
23 }
24 outreal[k] = sumreal;
25 outimag[k] = sumimag;
26 }
27 }
28
29}برنامه تبدیل فوریه گسسته در C
1/*
2 * Discrete Fourier transform (C)
3 * by Project Nayuki, 2017. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7
8/*
9 * Computes the discrete Fourier transform (DFT) of the given complex vector.
10 * All the array arguments must be non-NULL and have a length equal to n.
11 */
12#include <complex.h>
13#include <math.h>
14void compute_dft_complex(const double complex input[], double complex output[], int n) {
15 for (int k = 0; k < n; k++) { // For each output element
16 complex double sum = 0.0;
17 for (int t = 0; t < n; t++) { // For each input element
18 double angle = 2 * M_PI * t * k / n;
19 sum += input[t] * cexp(-angle * I);
20 }
21 output[k] = sum;
22 }
23}
24
25
26/*
27 * (Alternate implementation using only real numbers.)
28 * Computes the discrete Fourier transform (DFT) of the given complex vector.
29 * All the array arguments must be non-NULL and have a length equal to n.
30 */
31#include <math.h>
32void compute_dft_real_pair(const double inreal[], const double inimag[],
33 double outreal[], double outimag[], int n) {
34
35 for (int k = 0; k < n; k++) { // For each output element
36 double sumreal = 0;
37 double sumimag = 0;
38 for (int t = 0; t < n; t++) { // For each input element
39 double angle = 2 * M_PI * t * k / n;
40 sumreal += inreal[t] * cos(angle) + inimag[t] * sin(angle);
41 sumimag += -inreal[t] * sin(angle) + inimag[t] * cos(angle);
42 }
43 outreal[k] = sumreal;
44 outimag[k] = sumimag;
45 }
46}برنامه تبدیل فوریه گسسته در C++
1/*
2 * Discrete Fourier transform (C++)
3 * by Project Nayuki, 2017. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7// Shared definitions
8#include <cmath>
9#include <vector>
10using std::size_t;
11using std::vector;
12
13
14/*
15 * Computes the discrete Fourier transform (DFT) of the given complex vector.
16 * All the array arguments must have the same length.
17 */
18#include <complex>
19using std::complex;
20using std::exp;
21vector<complex<double> > computeDft(const vector<complex<double> > &input) {
22 vector<complex<double> > output;
23 size_t n = input.size();
24 for (size_t k = 0; k < n; k++) { // For each output element
25 complex<double> sum(0.0, 0.0);
26 for (size_t t = 0; t < n; t++) { // For each input element
27 double angle = 2 * M_PI * t * k / n;
28 sum += input[t] * exp(-angle);
29 }
30 output.push_back(sum);
31 }
32 return output;
33}
34
35
36/*
37 * (Alternate implementation using only real numbers.)
38 * Computes the discrete Fourier transform (DFT) of the given complex vector.
39 * All the array arguments must have the same length.
40 */
41using std::cos;
42using std::sin;
43void computeDft(const vector<double> &inreal, const vector<double> &inimag,
44 vector<double> &outreal, vector<double> &outimag) {
45
46 size_t n = inreal.size();
47 for (size_t k = 0; k < n; k++) { // For each output element
48 double sumreal = 0;
49 double sumimag = 0;
50 for (size_t t = 0; t < n; t++) { // For each input element
51 double angle = 2 * M_PI * t * k / n;
52 sumreal += inreal[t] * cos(angle) + inimag[t] * sin(angle);
53 sumimag += -inreal[t] * sin(angle) + inimag[t] * cos(angle);
54 }
55 outreal[k] = sumreal;
56 outimag[k] = sumimag;
57 }
58}برنامه تبدیل فوریه گسسته در C#
1/*
2 * Discrete Fourier transform (C#)
3 * by Project Nayuki, 2017. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7using System;
8using System.Numerics; // For Complex
9
10
11public sealed class Dft {
12
13 /*
14 * Computes the discrete Fourier transform (DFT) of the given complex vector.
15 */
16 public static Complex[] computeDft(Complex[] input) {
17 int n = input.Length;
18 Complex[] output = new Complex[n];
19 for (int k = 0; k < n; k++) { // For each output element
20 Complex sum = 0;
21 for (int t = 0; t < n; t++) { // For each input element
22 double angle = 2 * Math.PI * t * k / n;
23 sum += input[t] * Complex.Exp(new Complex(0, -angle));
24 }
25 output[k] = sum;
26 }
27 return output;
28 }
29
30
31 /*
32 * Computes the discrete Fourier transform (DFT) of the given complex vector.
33 * All the array arguments must be non-null and have the same length.
34 */
35 public static void computeDft(double[] inreal, double[] inimag, double[] outreal, double[] outimag) {
36 int n = inreal.Length;
37 for (int k = 0; k < n; k++) { // For each output element
38 double sumreal = 0;
39 double sumimag = 0;
40 for (int t = 0; t < n; t++) { // For each input element
41 double angle = 2 * Math.PI * t * k / n;
42 sumreal += inreal[t] * Math.Cos(angle) + inimag[t] * Math.Sin(angle);
43 sumimag += -inreal[t] * Math.Sin(angle) + inimag[t] * Math.Cos(angle);
44 }
45 outreal[k] = sumreal;
46 outimag[k] = sumimag;
47 }
48 }
49
50}برنامه تبدیل فوریه گسسته در JavaScript
1/*
2 * Discrete Fourier transform (JavaScript)
3 * by Project Nayuki, 2018. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7"use strict";
8
9
10/*
11 * Computes the discrete Fourier transform (DFT) of the given complex vector.
12 * 'inreal' and 'inimag' are each an array of n floating-point numbers.
13 * Returns an array of two arrays - outreal and outimag, each of length n.
14 */
15function computeDft(inreal, inimag) {
16 var n = inreal.length;
17 var outreal = new Array(n);
18 var outimag = new Array(n);
19 for (var k = 0; k < n; k++) { // For each output element
20 var sumreal = 0;
21 var sumimag = 0;
22 for (var t = 0; t < n; t++) { // For each input element
23 var angle = 2 * Math.PI * t * k / n;
24 sumreal += inreal[t] * Math.cos(angle) + inimag[t] * Math.sin(angle);
25 sumimag += -inreal[t] * Math.sin(angle) + inimag[t] * Math.cos(angle);
26 }
27 outreal[k] = sumreal;
28 outimag[k] = sumimag;
29 }
30 return [outreal, outimag];
31}برنامه تبدیل فوریه گسسته در TypeScript
1/*
2 * Discrete Fourier transform (TypeScript)
3 * by Project Nayuki, 2018. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7"use strict";
8
9
10/*
11 * Computes the discrete Fourier transform (DFT) of the given complex vector.
12 * 'inreal' and 'inimag' are each an array of n floating-point numbers.
13 * Returns an array of two arrays - outreal and outimag, each of length n.
14 */
15function computeDft(inreal: Array<number>, inimag: Array<number>): [Array<number>,Array<number>] {
16 const n: number = inreal.length;
17 let outreal: Array<number> = new Array(n);
18 let outimag: Array<number> = new Array(n);
19 for (let k = 0; k < n; k++) { // For each output element
20 let sumreal: number = 0;
21 let sumimag: number = 0;
22 for (let t = 0; t < n; t++) { // For each input element
23 const angle: number = 2 * Math.PI * t * k / n;
24 sumreal += inreal[t] * Math.cos(angle) + inimag[t] * Math.sin(angle);
25 sumimag += -inreal[t] * Math.sin(angle) + inimag[t] * Math.cos(angle);
26 }
27 outreal[k] = sumreal;
28 outimag[k] = sumimag;
29 }
30 return [outreal, outimag];
31}برنامه تبدیل فوریه گسسته در Python
1#
2# Discrete Fourier transform (Python)
3# by Project Nayuki, 2017. Public domain.
4# https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5#
6
7
8#
9# Computes the discrete Fourier transform (DFT) of the given complex vector.
10# 'input' is a sequence of numbers (integer, float, or complex).
11# Returns a list of complex numbers as output, having the same length.
12#
13import cmath
14def compute_dft_complex(input):
15 n = len(input)
16 output = []
17 for k in range(n): # For each output element
18 s = complex(0)
19 for t in range(n): # For each input element
20 angle = 2j * cmath.pi * t * k / n
21 s += input[t] * cmath.exp(-angle)
22 output.append(s)
23 return output
24
25
26#
27# (Alternate implementation using only real numbers.)
28# Computes the discrete Fourier transform (DFT) of the given complex vector.
29# 'inreal' and 'inimag' are each a sequence of n floating-point numbers.
30# Returns a tuple of two lists of floats - outreal and outimag, each of length n.
31#
32import math
33def compute_dft_real_pair(inreal, inimag):
34 assert len(inreal) == len(inimag)
35 n = len(inreal)
36 outreal = []
37 outimag = []
38 for k in range(n): # For each output element
39 sumreal = 0.0
40 sumimag = 0.0
41 for t in range(n): # For each input element
42 angle = 2 * math.pi * t * k / n
43 sumreal += inreal[t] * math.cos(angle) + inimag[t] * math.sin(angle)
44 sumimag += -inreal[t] * math.sin(angle) + inimag[t] * math.cos(angle)
45 outreal.append(sumreal)
46 outimag.append(sumimag)
47 return (outreal, outimag)برنامه تبدیل فوریه گسسته در Rust
1/*
2 * Discrete Fourier transform (Rust)
3 * by Project Nayuki, 2017. Public domain.
4 * https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5 */
6
7
8fn compute_dft(inreal: &[f64], inimag: &[f64], outreal: &mut [f64], outimag: &mut [f64]) {
9 let n: usize = inreal.len();
10 for k in 0 .. n { // For each output element
11 let mut sumreal: f64 = 0.0;
12 let mut sumimag: f64 = 0.0;
13 for t in 0 .. n { // For each input element
14 let angle: f64 = 2.0 * std::f64::consts::PI
15 * (t as f64) * (k as f64) / (n as f64);
16 sumreal += inreal[t] * angle.cos() + inimag[t] * angle.sin();
17 sumimag += -inreal[t] * angle.sin() + inimag[t] * angle.cos();
18 }
19 outreal[k] = sumreal;
20 outimag[k] = sumimag;
21 }
22}برنامه تبدیل فوریه گسسته در MATLAB
1%
2% Discrete Fourier transform (MATLAB)
3% by Project Nayuki, 2017. Public domain.
4% https://www.nayuki.io/page/how-to-implement-the-discrete-fourier-transform
5%
6
7
8%
9% Computes the discrete Fourier transform (DFT) of the given complex vector.
10% 'input' can be a row vector or a column vector. The returned output has the same dimensions.
11%
12function output = compute_dft_scalarized(input)
13 assert(isvector(input));
14 n = numel(input);
15 output = NaN(size(input));
16 for k = 0 : n - 1 % For each output element
17 s = 0;
18 for t = 0 : n - 1 % For each input element
19 s = s + input(t + 1) * exp(-2i * pi * t * k / n);
20 end
21 output(k + 1) = s;
22 end
23end
24
25
26%
27% (Alternate implementation using matrix arithmetic.)
28% Computes the discrete Fourier transform (DFT) of the given complex vector.
29% 'input' can be a row vector or a column vector. The returned output has the same dimensions.
30%
31function output = compute_dft_vectorized(input)
32 assert(isvector(input));
33 n = numel(input);
34 matrix = exp(-2i * pi / n * (0 : n-1)' * (0 : n-1));
35 if size(input, 1) == 1 % Row vector
36 output = input * matrix;
37 elseif size(input, 2) == 1 % Column vector
38 output = matrix * input;
39 end
40endجمعبندی
- تبدیل فوریه گسسته یکی از قویترین ابزارهای پردازش سیگنال دیجیتال است که به ما این امکان را میدهد طیف سیگنال متناهی را پیدا کنیم.
- اساساً، محاسبه DFT معادل با حل مجموعهای از معادلات خطی است.
- تبدیل فوریه گسسته با استفاده از یک دنباله متناوب نمایشی از یک دنباله متناهی در اختیار ما قرار میدهد. یک دوره تناوب دنباله متناوب مشابه با دنباله متناهی است. در نتیجه، میتوانیم از سری فوریه زمانگسسته برای استخراج معادلات DFT استفاده کنیم.
اگر مطلب بالا برای شما مفید بوده و علاقهمند به موضوعات مرتبط با آن هستید، پیشنهاد میکنیم آموزشهای زیر را نیز ببینید:
- تبدیل فوریه سریع (fft) — به زبان ساده
- تابع تبدیل پالسی — از صفر تا صد
- سری فوریه مختلط — به زبان ساده
^^













با سلام
بسیار عالی
فقط یک باید بگم در ابتدای بحث، تعداد نمونه برداری شما 1600 نقطه بر ثانیه است یعنی 1600 هرتز است. که اشتباها تایپ شده 8000 هرتز.
زیرا کل شکل 1، 5 میلی ثانیه است و 8 نمونه گرفته شده
8 تقسیم بر 5 میلی ثانیه میشه.. 1600 هرتز
پریود تابع آنالوگ 1 میلی ثانیه هست که با نرخ نمونه برداری 8000 مورد بر ثانیه، زمان بین دو نمونه متوالی 1/8000 ثانیه خواهد بود که اگر 8 نمونه را لحاظ کنیم، به یک سیکل کامل میرسیم.
با سلام؛
متن بازبینی شد و صحیح است.
با تشکر از همراهی شما با مجله فرادرس
چقدر روان مثال زدید و توضیح دادید… یکی از مباحث مهم در پردازش سیگنال نحوه پیاده سازی تبدیل فوریه هست که به ساده ترین شکل اون رو انجام دادید. سپاسگزارم
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
شاد و پیروز باشید.
سلام
روز بخیر
عااالی بود کاملا متوجه شدم.
ممنون