توزیع تجمعی — به زبان ساده

در مطالب گذشته وبلاگ فرادرس توزیعهای آماری مختلفی را توضیح دادیم. مهمترین آنها، توزیعهای نرمال، پواسون، برنولی و هندسی بودند. در این مطلب نیز قصد داریم تا یکی از توزیعهای پرکاربرد تحت عنوان تابع توزیع تجمعی را معرفی کرده و مثالهایی نیز از آن ارائه دهیم.
توزیع تجمعی
یکی از راههای توصیف توزیع متغیرهای گسسته، استفاده از تابع جرم احتمال (PMF) است. بهطور دقیقتر میتوان گفت که تابع جرم احتمال را نمیتوان برای متغیرهای تصادفی پیوسته تعریف کرد. تابع توزیع تجمعی (CDF) مربوط به یک متغیر تصادفی، راه جایگزینی بهمنظور توصیف متغیرهای تصادفی است.
مزیت تابع توزیع تجمعی این است که میتوان آن را برای هر نوع از متغیر تصادفی تعریف کرد. تابع توزیع تجمعی برای متغیر تصادفی ، مطابق با گزاره زیر تعریف میشود.
اجازه دهید بهمنظور درک بهتر مثالی کمی را مطرح کنیم که در ادامه نحوه حل آن نیز ارائه شده است.
مثال ۱
سکهای را در نظر بگیرید که دوبار آن را پرتاب میکنیم. فرض کنید تعداد دفعاتی است که شیر میآید. در این صورت تابع توزیع تجمعی را بیابید. در اولین گام باید بگوییم که آزمایش برای دوبار انجام میشود. در هریک از این آزمایشها نیز احتمال شیر یا خط بودن برابر با ۵۰ درصد است. بنابراین میتوان گفت:
در حقیقت متغیر میتواند هریک از حالات زیر را داشته باشد ( نشاندهنده تعداد دفعاتی است که شیر یا خط ظاهر میشود).
احتمال هریک از حالات فوق نیز برابر است با:
بهمنظور یافتن تابع توزیع تجمعی به صورت زیر عمل میکنیم. بدیهی است که مقدار نمیتواند منفی باشد. از این رو این حالت را میتوان مطابق با گزاره زیر بیان کرد:
در حالتی که باشد نیز احتمال رخداد برابر با است. در نتیجه این حالت را میتوان بهصورت زیر بیان کرد:
حالت نهایی نیز زمانی است که در بازه قرار داشته باشد. در این حالت احتمال رخداد برابر است با:
در نتیجه نهایتا میتوان تابع توزیع احتمال مربوط به این دو پرتاب را در قالب تابع چندضابطهای زیر بیان کرد:
توجه داشته باشید هنگامی که از شما خواسته میشود که تابع توزیع تجمعی یک متغیر تصادفی را بیابید، شما باید تابع را به ازای تمامی خط حقیقی بیابید. همچنین در مورد متغیرهای تصادفی گسسته در هنگام استفاده از ">" و "<" باید دقت داشته باشید. شکل ارائه شده در زیر نشاندهنده تابع است.
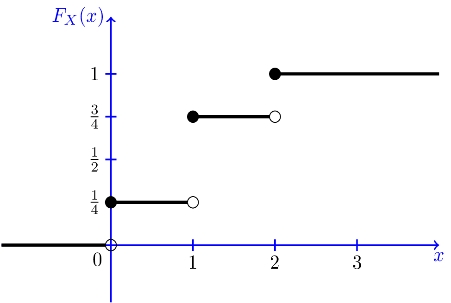
همانطور که در نمودار فوق نیز نشان داده شده مقدار تابع توزیع به ازای مقادیر صحیح بهصورت خط صاف بوده و تنها در مقادیر صحیح دارای ناپیوستگی است. نکته دیگر آن است که اندازه پرش در هر نقطه برابر با میزان احتمال در آن نقطه است. برای نمونه احتمال به ازای برابر با است (). از این رو در این نقطه اندازه پرش نیز به همین میزان است.
حال حالتی کلیتر را بررسی میکنیم. در این حالت فرض کنید متغیری تصادفی و گسسته باشد که بتواند هریک از مقادیر را اختیار کند. توجه داشته باشید که متغیرها بهترتیب از کوچک به بزرگ نوشته شدهاند.
همچنین بهمنظور سادگی بیشتر فرض بر این است که از پایین به مقدار محدود شده و این عدد کوچکترین مقدار در باشد. در شکل زیر تابع توزیع احتمال یا برای چنین توزیعی نشان داده شده است.
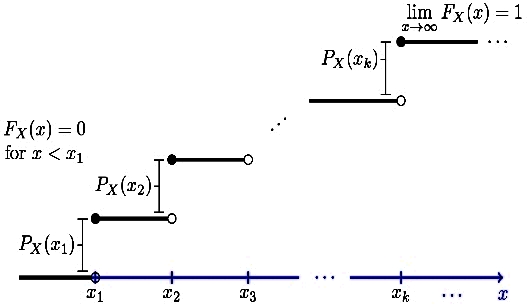
همانطور که مشاهده میکنید تابع توزیع در چنین حالتی بهصورت پلهای است. تابع پلهای در این حالت از صفر شروع شده و همانند مثال بین مقادیر صحیح بهصورت صاف است. از این رو میتوان تابع را بین دو مقدار و مطابق با رابطه زیر بیان کرد:
همانطور که در بالا نیز بیان شده اندازه پرش در برابر با احتمال رخداد در است. در نتیجه میتوان رابطه زیر را بیان کرد:
به اندازه کافی کوچک
بنابراین تابع توزیع احتمال همواره تابعی غیرکاهشی محسوب میشود. این جمله به معنای آن است که اگر بیشتر از باشد ()، در این صورت نیز بیشتر از است (). نهایتا و در حالتی حدی نیز میتوان گفت:
توجه داشته باشید که تابع توزیع تجمعی بهطور کامل نحوه توزیع متغیر تصادفی و گسسته را توصیف میکند. با استفاده از این نمودار، تابع جرم احتمال یا همان را نیز بهراحتی میتوان بدست آورد. همانند بالا اگر فضای را بهصورت در نظر بگیریم، میتوان رابطه بین دو توزیع را به شکل زیر بیان کرد:
حال میخواهیم رابطهای را اثبات کنیم که از آن در محاسبه توزیع تجمعی بسیار استفاده میشود. این رابطه با فرض ، بهصورت زیر است.
بهمنظور اثبات رابطه فوق در ابتدا باید بدانید که در حالت میتوان رابطه زیر را برای احتمال نوشت:
در نتیجه رابطه فوق را میتوان بر حسب تابع توزیع تجمعی، بهصورت زیر بازنویسی کرد:
در این حالت نیز باید به تفاوت دو علامت "" و " " توجه داشته باشید چراکه مفهوم آنها در موارد استفاده از متغیرهای تصادفی گسسته متفاوت است. در آینده نشان خواهیم داد که معادله ارائه شده در بالا برای انواع مختلف متغیرهای تصادفی درست خواهد بود. توجه داشته باشید که تابع توزیع تجمعی تنها به ما را میدهد. بهمنظور حذف کردن تساوی در نامساوی و یافتن ، برای یک متغیر تصادفی گسسته، کافی است از رابطه زیر استفاده کنید.
مثال ۲
فرض کنید متغیری گسسته و تصادفی با برد باشد. همچنین فرض کنید تابع جرم احتمالِ نیز مطابق با رابطه زیر محاسبه شود.
در این صورت موارد زیر را بیابید.
- تابع توزیع تجمعیِ ()
- تابع در بازه
- تابع در بازه
در ابتدا خوب است بدانید که رابطه ارائه شده بهراستی نشاندهنده تابع توزیع احتمال است. چراکه حاصل جمع مقادیر آن برابر است با:
جمع هندسی
مقادیر تابع توزیع احتمال در هریک از بازهها برابر است با:
در حالت کلی داریم:
شکل زیر نشاندهنده تابع توزیع بدست آمده است.
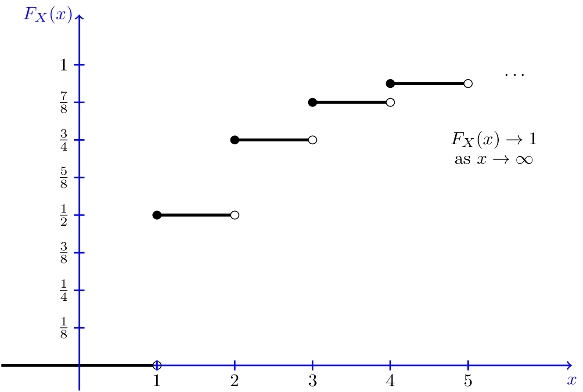
را میتوان بهصورت زیر بدست آورد.
البته مقدار فوق را میتوان با استفاده از مفهوم احتمال نیز بهصورت زیر بدست آورد.
همانطور که مشاهده میکنید این روش نیز همان پاسخ را به ما میدهد. نهایتا برای بدست آوردن نیز میتوان از مفهوم مجموع مقادیر احتمال بهره برد. با استفاده از این مفهوم داریم:
در مطالب آینده وبلاگ فرادرس در مورد دیگر توابع احتمال نیز بحث کرده و کابردهای تابع توزیع احتمال تجمعی را بیشتر معرفی خواهیم کرد.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی و آمار، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی
- مجموعه آموزشهای آمار و احتمالات
- توزیعهای آماری — مجموعه مقالات جامع وبلاگ فرادرس
- متغیر تصادفی و توزیع برنولی — به زبان ساده
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
^^












