انطباق امتیاز گرایش در آمار | به زبان ساده

در آمار و تحلیل داده‌ها، «انطباق امتیاز گرایش» (Propensity score matching) یک روش مطابقت آماری است که سعی دارد اثر تیمار‌ها را به کمک متغیرهای همبسته (Covariates) پیش‌بینی کند. در روش انطباق امتیاز گرایش، اریبی (Bias) نسبت به مقایسه‌های ساده‌ای که روی نتایج یا اثر تیمارها اجرا می‌شود، کاهش یافته و اثر متغیرهای همبسته و مزاحم در این میان از بین می‌رود.

به منظور آشنایی با روش‌های مطابقت براساس ماتریس همبستگی (Correlation Matrix) بهتر است نوشتارهای دیگر مجله فرادرس را با عناوین، ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده و کوواریانس و نحوه محاسبه آن — به زبان ساده بخوانید. همچنین خواندن مطلب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و نیز نوشتار وابستگی، کوواریانس و ضریب همبستگی در علم داده — راهنمای کاربردی نیز خالی از لطف نیست.

انطباق امتیاز گرایش

یکی از علت‌های ظهور «اریبی» (Bias) در تعیین اثر «تیمار» (Treatments)، استفاده از مقایسه نتایج حاصل از گروه‌های تیمار شده و تیمار نشده است که به کمک یک متغیر عامل تعیین می‌شود. در این حالت به جای اندازه‌گیری اثر تیمار، «پیش‌بینی اثر تیمار» (Predict Treatment) صورت می‌گیرد.

روش تطبیق امتیاز گرایش (PSM) توسط دو دانشمند و آمارشناس آمریکایی «روزن‌بام» (Paul Rosenbaum) و «روبین» (Donald Rubin) طی مقاله‌ای که در مجله «بایومتریکا» (Biometrica) در سال ۱۹۸۳ منتشر کردند، معرفی و به کار گرفته شد.

یکی از روش‌های از بین بردن اریبی در چنین حالتی استفاده از «طرح آزمایشات تصادفی شده» (Randomized Experiments) است. به این ترتیب برای هر «متغیر همبسته» (Covariate Variable)، تصادفی‌سازی به کار رفته که بین گروه‌های تیمار شده یک تعادل ایجاد می‌کند. این امر یکی از نتایج حاصل از قانون اعداد بزرگ (Law of Large Numbers) است.

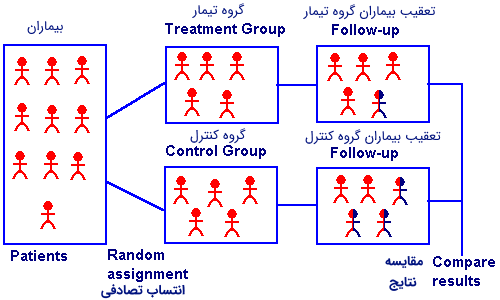
متاسفانه تحلیل براساس مشاهدات، به سادگی تصادفی‌سازی نمی‌شوند، به همین دلیل تطبیق دادن، سعی دارد که اریبی حاصل از نسبت دادن افراد به تیمارها را کاهش دهد. این کار بوسیله انجام عملیاتی شبه تصادفی صورت می‌گیرد. به این ترتیب نمونه‌ای از واحدهای مشاهده شده که تیمار را دریافت کرده‌اند و گروهی که تیمار رویشان اثر نکرده، تهیه شده و میزان همبستگی بین آن‌ها محاسبه می‌شود.

برای مثال فرض کنید محققی علاقه به تعیین اثر سیگار کشیدن روی سلامتی افراد دارد. مشخص است که یک «مطالعه مشاهده‌ای» یا «مطالعه بالینی» (Observational Study) نیاز است؛ زیرا نمی‌توان افراد را به زور سیگاری و غیرسیگاری کرد و از بین آن‌ها یک طرح کاملا تصادفی را اجرا نمود. در نتیجه انتخاب افراد سیگاری در گروه سیگاری‌ها و غیرسیگاری در گروه غیرسیگاری‌ها ضروری است.

به این ترتیب افرادی که سیگاری هستند به دسته سیگاری‌ها و کسانی که دخانیات استعمال نمی‌کنند در دسته غیرسیگاری طبقه‌بندی می‌شوند. بنابراین اثر سیگار بر سلامتی به سادگی با مقایسه افراد سیگاری و غیرسیگاری صورت می گیرد. این کار باعث می‌شود که عامل‌های دیگر (متغیرهای همبسته و مداخله‌گر) که روی پیش‌بینی سیگاری بودن اثر دارند، اریبی ایجاد کنند. مثلا سن و جنسیت از فاکتورهایی هستند که ممکن است روی سیگاری بودن افراد تاثیرگذار باشند.

تطبیق امتیاز گرایش (Propensity score matching) که گاهی به اختصار آن را PSM‌ نیز می‌نامند، باعث کنترل این عوامل شده و اثر تیمار را با مقایسه بین دو گروه تیمار و غیرتیمار با کنترل متغیرهای همبسته و مداخله‌گر، محاسبه می‌کند.

تکنیک‌های مورد نیاز در انطباق امتیاز گرایش

روش PSM یه عنوان یک تکنیک علت و معلولی شناخته می‌شود و برای مقایسه بین مشاهدات تیمار شده و غیر تیمار و اندازه‌گیری اثر تیمارها با کمترین میزان اریبی، مناسب است. زیرا، با انتخاب چند نمونه از گروه غیرتیماری با چند واحد از گروه تیمار، قابلیت مقایسه بوجود می‌آید. از طرفی انتخاب همه واحدهای گروه تیمار و غیر تیمار امکان‌پذیر نیست. این امر به این علت رخ می‌دهد که تعداد ترکیب‌ها در زمانی که ابعاد مشاهدات (متغیرهای مربوط به بررسی) بزرگ باشند، عملا بسیار زیاد شده و امکان بررسی همه موارد وجود ندارد.

در تطابق عادی (Normal Matching)، یک ویژگی خاص که گروه‌های تیمار و کنترل را از هم متمایز می‌کند، برای تشکیل گروه‌های همسان به کار می‌رود. اما اگر دو گروه، همپوشانی قابل توجهی نداشته باشند، ممکن است خطای اریبی در پیش‌بینی وارد شود. به عنوان مثال، اگر تنها بدترین موارد از گروه تیمار نشده فقط با بهترین موارد از گروه تیمار مقایسه شود، نتیجه ممکن است به سمت میانگین تمایل پیدا کند، که باعث شود گروه کنترل بهتر یا بدتر از حالت واقعیت به نظر برسد.

تکنیک PSM، احتمال عضویت در گروه (به عنوان مثال، گروه تیمار در مقابل گروه کنترل) را براساس مشاهدات پیش‌بینی می‌کند. این کار معمولا به کمک «رگرسیون لجستیک» (Logistic Regression) انجام شده و یگ گروه متناقض تولید می‌شود. امتیازات گرایش یا تمایل ممکن است بر اساس متغیر همبسته یا مداخله‌گر محاسبه شده و به عنوان ابزاری برای مطابقت به کار رود.

روند اجرای انطباق امتیاز گرایش

به منظور اجرای تکنیک تطبیق امتیاز گرایش (PSM)، گام‌ها و زیرگام‌هایی که در ادامه مشخص شده‌اند باید به صورت مرحله به مرحله و گام به گام، انجام شوند.

اجرای رگرسیون لجستیک

از آنجایی که بعضی از مشاهدات از نمونه اولیه برای تکنیک تطابق گرایش، جدا شده‌اند، رگرسیون لجستیک را برای مدل‌سازی متغیرهای مداخله‌گر، وابسته و مستقل به صورت زیر به کار می‌گیریم.

• تعیین متغیر وابسته به صورت $$Z=1$$ به شرطی که مشاهده خاص در PSM به کار رفته باشد و $$Z=0$$‌ در غیر اینصورت.
• تعیین متغیر همبسته (Covariate). فرض بر این است که متغیر همبسته (یا حتی متغیر مخدوش کننده) هم بر تیمار و هم بر نتایج (متغیر وابسته) تاثیر گذار است.
• برآورد امتیاز گرایش به کمک رگرسیون لجستیک و برآورد احتمال قرار گرفتن در گروه $$Z=1$$ که با نماد $$p$$‌ مشخص شده یا محاسبه $$\log(\frac{p}{1-p)}$$ که لگاریتم «بخت» (Odds Ratio) محسوب می‌شود.

بررسی متعادل بودن امتیاز گرایش

محاسبات مربوط به تعادل باید در بین هر دو گروه تیمار و کنترل صورت گیرد. به همین دلیل دسته‌بندی‌های زیر را برای انجام این امر معرفی کرده‌ایم.

• بررسی متعادل بودن امتیاز گرایش در بین گروه‌های تیمار و کنترل.
• بررسی تعادل مقدار متغیر همبسته در بین دو سطح گروه تیمار و گروه کنترل در بین کل مقادیر امتیازات گرایش.
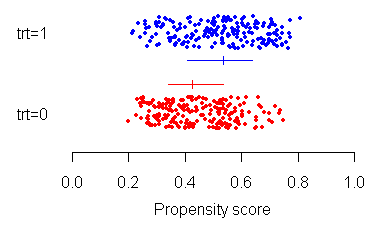
• استفاده از اختلاف امتیازات استاندارد شده برای نمایش توزیع مقادیر امتیاز گرایش یا رسم نمودار توزیع به منظور بررسی تعادل.

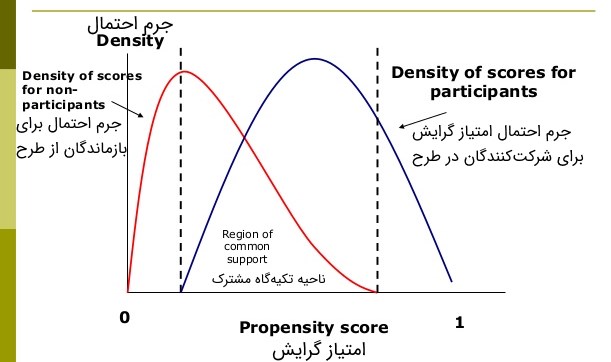
انطباق هر مشاهده خاص با مشاهدات با کد $$Z=0$$ و با یک روش خاص

برای انجام این کار می‌توان از روش‌های مطابقتی که در ادامه معرفی می‌شوند، استفاده کرد.

• استفاده از روش انطباق نزدیکترین همسایه (Nearest neighbor matching).
• انطباق کولیس (Caliper Matching): واحدهای مقایسه‌ای براساس فاصله مشخص از امتیاز گرایش با واحدهای تیمار شده که انطباق دارند. فاصله در اینجا می‌تواند نسبتی از انحراف استاندارد امتیاز گرایش باشد.
• محاسبه فاصله ماهالانوبیس (Mahalanobis Metric) مرتبط با امتیاز انطباق.
• انطباق طبقه‌ای (Stratification Matching).
• مطابقت اختلاف به اختلاف (با استفاده از هسته (Kernel) و «وزن‌های خطی محلی» (Local Linear Weights) برای وزن دادن به گروه‌ها).
• انطباق ساده (Exact Matching)، بطوری که درصد انطباق براساس تمامی متغیرها با مقادیر یکسان به کار می‌رود.

تعاریف ضروری در انطباق امتیاز گرایش

اصطلاحات و تعریفی در تحلیل انطباق امتیاز گرایش وجود دارد که در ادامه به بعضی از آن‌ها اشاره کرده و توضیحات کاملی در موردشان ارائه خواهیم داد. این اصطلاحات در بعضی از برنامه‌های کاربردی برای اجرای چنین تحلیلی، به کار برده می‌شوند. در نتیجه آگاهی از آن‌ها هنگام کار با این گونه نرم‌افزارها، ضروری است.

تنظیمات اولیه (Basic Settings)

هر مشاهده پایه (Basic Case) یا اصلی برای متغیر وابسته، به صورت دو مقدار صفر و یک با در نظر گرفتن وجود تیمار یا عدم آن در آن مشاهده، مشخص می‌شود. هر یک از مشاهدات، دارای متغیرهایی هم توزیع، و مستقل هستند. حجم نمونه در این حالت برابر با $$N$$ در نظر گرفته می‌شود. هر یک از مشاهدات با توجه به قرار گرفتن در تیمار به صورت $$r_{1i}$$ و در صورت حضور در گروه کنترل به شکل $$r_{0i}$$‌ مشخص خواهد شد. کمیتی که باید مورد محاسبه قرار گیرد، اختلاف بین میانگین گروه تیمار و کنترل است که بر حسب امید ریاضی به شکل $$E[r_1]- E[r_0]$$ نشان داده می‌شود.

متغیر نشانگر $$Z_i$$ بیانگر آن است که مشاهده در گروه تیمار است یا کنترل در این حالت $$Z=1$$ و $$Z=0$$ تعریف می‌شود. فرض کنید که $$X_i$$ بردار متغیرها برای مشاهده $$i$$ام، قبل از اجرای تیمار برای متغیرهای مورد بررسی (به همراه متغیرها مداخله‌گر- Covariate) باشد. البته توجه داشته باشید که متغیرهای موجود در $$X_i$$ ممکن است شامل همه متغیرهای مربوط به تیمارها نباشند. همچنین مشخص بودن شماره مشاهده ارتباطی با متغیرهای موجود در آن مشاهده ندارد. این امر به این معنی است که متغیرها مستقل از ترتیب مشاهدات هستند.

نکته: توجه داشته باشید که هدف اصلی در تکنیک انطباق امتیاز گرایش، از بین بردن ارتباط بین شماره مشاهدات و متغیرهای موجود در آن است. بطوری که بین انتخاب در گروه تیمار یا غیرتیمار ارتباطی وجود نداشته تا باعث کاهش اریبی در نتایج بررسی تیمار شود.

نادیده گرفتن نسبت دادن تیمار به مشاهدات

فرض کنید بعضی از مشاهدات دارای بردار متغیرهای همبسته $$X$$ (به شرط مداخله‌گر نبودن) باشند. نتایج حاصل از این متغیرها نیز تحت تیمار و گروه کنترل به صورت $$r_0$$ و $$r_1$$ مشخص شده است.

نسبت دادن تیمار به مشاهدات به صورت قوی، قابل نادیده گرفتن (Strongly Ignorable Treatment Assignment) است، اگر نتایج متغیر وابسته، مستقل از تیمار به شرط متغیرهای پس زمینه یا همبسته $$X$$ باشد. این امر را به صورت زبان آماری به شکل زیر نمایش می‌دهیم.

$$ \large r_0 , r_1\ \bot\ Z\ |\ X$$

توجه دارید که نماد $$\bot$$ نشانگر استقلال دو متغیر و نماد $$|$$‌ نیز توزیع احتمال شرطی را نشان می‌دهد.

امتیاز تعادل

تابعی از مشاهدات حاصل از متغیرهای همبسته (Covariates) که با نماد $$X$$‌ نشان دادیم، می‌تواند تابع امتیاز تعادل ($$b(X)$$) باشد. توزیع $$X$$ به شرط $$b(X)$$ باید برای $$Z=1$$ و $$Z=0$$ یکسان باشد. در حقیقت $$Z$$ و $$X$$ به شرط $$b(X)$$ باید مستقل از یکدیگر باشند. در این حالت شاید ساده‌ترین تابع «امتیاز تعادل» (Balancing Score) همان $$b(X)=X$$ باشد. در اینجا استقلال این دو متغیر را به صورت زیر نشان می‌دهیم.

$$ \large Z \ \bot \ X \ | \ b(X) $$

امتیاز گرایش

احتمال اینکه یک واحد از مورد تحقیق (فرد، کلاس درس، مدرسه) به یک تیمار اختصاص داده شود به شرط متغیر همبسته، «امتیاز گرایش» (Propensity Score) نامیده می‌شود. امتیاز گرایش، باعث کاهش اریبی در انتخاب مشاهدات می‌شود. این کار بوسیله یکسان سازی گروه‌ها براساس متغیرهای همبسته صورت می‌گیرد.

فرض کنید که متغیر نشانگر $$Z$$، متغیر پاسخ $$r$$ و متغیرهای همبسته دیگر که به صورت $$X$$‌ مشخص شده‌اند، در مدل حضور دارند. امتیاز گرایش به صورت احتمال شرطی تیمارها با مشخص بودن متغیرهای همبسته تعریف می‌شود. این تعریف در رابطه ریاضی زیر مشخص شده است.

$$ \large {\displaystyle e(x)\ {\stackrel {\mathrm {def} }{=}}\ \Pr(Z=1|X=x)} $$

قضیه اصلی در انطباق امتیاز گرایش

گزاره‌های زیر اولین بار توسط «روزن‌بام» (Rosenbaum) و «روبین» (Rubin) در سال ۱۹۸۳ معرفی و اثبات شدند.

• امتیاز گرایش $$e(X)$$ یک امتیاز تعادل است.
• هر تابعی از امتیاز گرایش، یک امتیاز تعادل است. این گزاره را به صورت $$e(X) = f(b(X)$$ نشان می‌دهیم. تابع $$f$$ می‌تواند هر تابعی در نظر گرفته شود.
• اگر انتساب تیمار به صورت قوی قابل نادیده گرفتن، برحسب $$X$$ باشد، آنگاه بر حسب هر تابع تعادل دیگر نیز قابل نادیده گرفتن است. بخصوص زمانی که این تابع تعادل همان امتیاز گرایش باشد. به بیان ریاضی خواهیم داشت:

$$ \large {\displaystyle (r_{0},r_{1})\perp Z\,|\,e(X)} $$

• با شرط نادیده گرفتن قوی با حضور $$X$$، برای هر امتیاز تعادل، اختلاف بین میانگین گروه تیمار و گروه کنترل ($$ \bar{r}_1 – \bar{r}_0 $$) براساس مشاهداتی که دارای امتیاز تعادل یکسانی هستند، می‌توان یک برآوردگر نااریب برای میانگین اثر تیمار ($$E(r_1) – E(r_0)$$) باشد.

مزایا و معایب انطباق امتیاز گرایش

می‌توان نشان داد که PSM باعث افزایش عدم تعادل، ناکارآمدی و همچنین وابستگی شدید پارامترها به مدل می‌شود. همچنین در بعضی از مواقع به جای کاهش اریبی، آن را افزایش نیز می‌دهد.

به همین دلیل در مقایسه با سایر روش‌های تطبیق توصیه نمی‌شود. به همین دلیل اغلب PSM را به همراه روش‌های دیگر تطبیق به کار می‌برند. هر چند وزن‌های تولید شده در تکنیک PSM باعث ایجاد برآوردگرهای استوار و قوی خواهد شد.

تکنیک PSM مانند سایر روش‌های تطبیق، متوسط اثر تیمار را براساس مشاهدات تخمین می‌زند. از مهمترین مزایای PSM در زمان معرفی آن، این بود كه با استفاده از ترکیبی خطی از متغیرهای مداخله‌گر برای یک امتیاز، باعث ایجاد تعادل در بین گروه‌های تیمار و كنترل شده و بدون از دست دادن تعداد زیادی از مشاهدات، این تعادل را برقرار می‌سازد.

اگر واحدهای موجود در تیمار و کنترل بر تعداد زیادی از متغیرهای همبستگی (مداخله‌گر) یک به یک دارای تعادل باشند، تعداد زیادی از مشاهدات برای غلبه بر مشکل ابعاد متغیرها لازم است. اضافه کردن یک متغیر همبسته، باعث رشد هندسی تعداد نمونه‌های خواهد شد.

یکی از مضرات PSM این است که فقط متغیرهای همبسته و مداخله‌گر با مقادیر مشاهده شده (و یا قابل مشاهده) را مورد بررسی قرار می‌دهد که به عنوان عوامل اثرگذار روی تیمارها و نتایج متغیر وابسته هستند. در حالیکه متغیرهای دیگری که از دید محقق دور مانده‌اند و به عنوان «متغیر پنهان» (Latent Variable) شناخته می‌شوند در این تکنیک جای نداشته و اریبی حاصل از آن‌ها حتی بعد از انطباق هم باقی می‌ماند.

پیاده سازی تحلیل مطابقت امتیاز گرایش در بسته های آماری

بسیاری از نرم‌افزارها و بسته‌های محاسبات آماری قادر به انجام تحلیل مطابقت امتیاز گرایش (PSM) هستند. در ادامه بعضی از آن‌ها را معرفی خواهیم کرد.

• در زبان محاسبات آماری R: انطباق امتیاز گرایش به عنوان بخشی از بسته MatchIt در زبان برنامه‌نویسی R در دسترس است. همچنین می‌توان آن را به راحتی به صورت دستی در این زبان برنامه‌نویسی پیاده سازی کرد.
• سیستم تحلیل آماری SAS: رویه یا تابع PSMatch و همچنین نسخه کلان داده آن به نام OneToManyMTCH نیز برای تجزیه و تحلیل انطباق امتیاز گرایش در نرم‌افزار آماری SAS وجود دارد.
• بسته نرم‌افزاری Stata: چندین فرمان انطباق امتیاز گرایش در Stata وجود دارد، از جمله psmatch2 نوشته شده توسط کاربر. نسخه ۱۳ نرم‌افزار Stata و همچنین نسخه‌های بعد از آن نیز دستورات داخلی برای اجرای این تحلیل را ارائه می‌دهد.
• بسته محاسبات آماری برای علوم اجتماعی SPSS: در نرم‌افزار SPSS، یک کادر محاوره‌ای برای تحلیل PSM دارد که براساس زبان برنامه‌نویسی پایتون پیاده سازی شده. در نتیجه باید به کمک افزونه‌های مورد نیاز آن را بارگذاری کرده و اجرا نمایید. افزونه FUZZY Python یکی از این گونه افزونه‌ها (Add-Ons) به حساب می‌آید. به منظور آشنایی با نحوه نصب افزونه‌های پایتون در SPSS بهتر است نوشتار افزونه های پایتون در SPSS – راهنمای کاربردی را مطالعه کنید.

خلاصه و جمع‌بندی

در این نوشتار با تحلیل انطباق امتیاز گرایش در آمار آشنا شدیم. مفاهیم اولیه و همچنین بعضی از اصطلاحات مربوط به این تحلیل و کاربردهای آن نیز مورد بررسی قرار گرفت. از آنجایی که محاسبات و عملیات مربوطه طولانی هستند در این متن به مثال عددی خاصی اشاره نکردیم و با داده‌های واقعی به PMS نپرداختیم. ولی در مورد نحوه اجرا و استفاده از این تحلیل در نرم‌افزار بسته آماری SPSS مطالبی در نوشتارهای بعدی مجله فرادرس، منتشر خواهیم کرد.