تشخیص داده پرت با فاصله ماهالانوبیس — پیاده سازی در پایتون
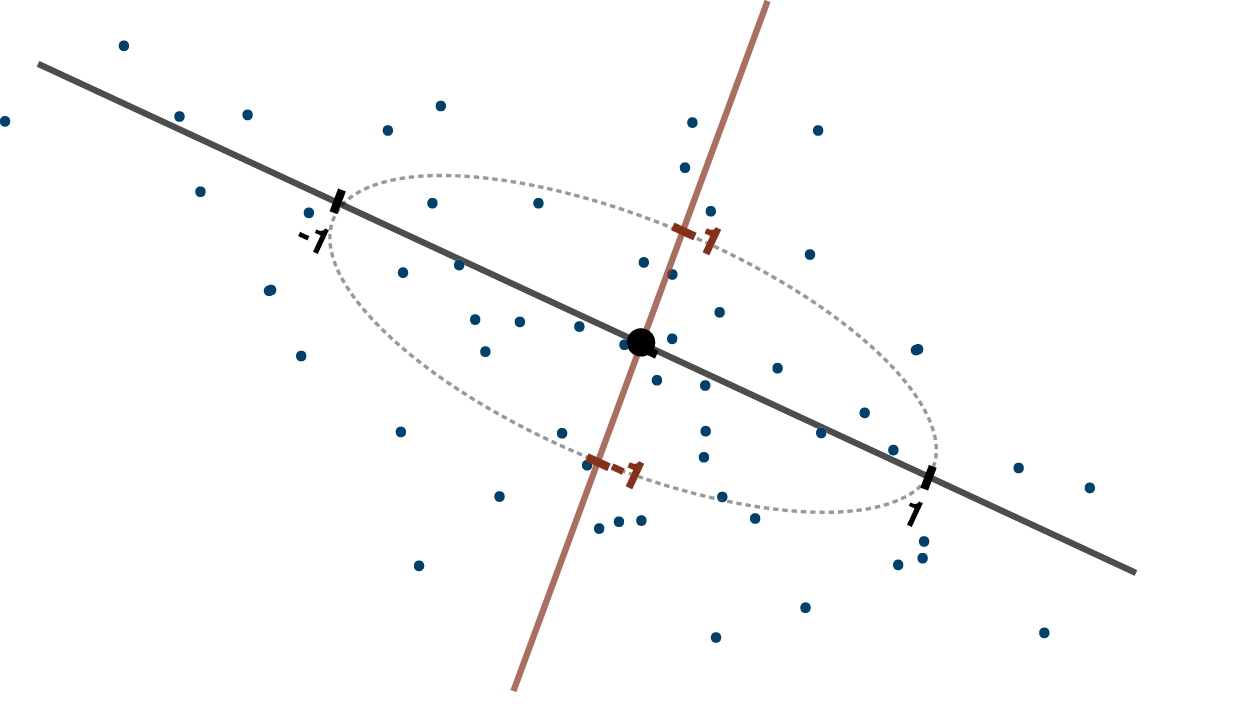
تشخیص «دادههای پرت و دورافتاده» (Outlier) در محاسبات و تجزیه و تحلیلهای دادهها، امری مهم محسوب میشود. از آنجایی که چنین دادههایی را از مدلهای آماری خارج میکنیم باید مطمئن باشیم که حذف آنها در پیشبینیهایی دنیای واقعی تاثیری نخواهد گذاشت و مدل ساخته شده به درستی عمل خواهد کرد. در این نوشتار به شناسایی داده پرت با فاصله ماهالانوبیس به کمک تکنیک PCA خواهیم پرداخت. برای انجام محاسبات نیز از زبان برنامهنویسی پایتون کمک خواهیم گرفت.
برای آشنایی با شیوههای دیگر تشخیص دادههای پرت بهتر است مطلب اعداد پرت (Outliers) – به زبان ساده و نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده را بخوانید. همچنین خواندن نوشتار تحلیل مولفه اساسی (PCA) در پایتون — راهنمای کاربردی و فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی نیز به عنوان پیشنیاز خالی از لطف نیست.
شناسایی داده پرت با فاصله ماهالانوبیس
با توجه به عنوانی که برای این نوشتار انتخاب شده، مشخص است که تابع فاصله ماهالانوبیس (Mahalanobis Distance) به عنوان روشی برای اندازهگیری فاصله مشاهدات از یکدیگر استفاده میشود. از طرفی برای کاهش بُعد دادهها و کم کردن تعداد متغیرها از تکنیک PCA یا «تحلیل مولفههای اصلی» (Principal Component Analysis) استفاده میکنیم. در این مرحله از دادههای مربوط به میزان تششع یک دستگاه اسپکترومتر استفاده کردهایم.
فرض کنید دادهها در فایلی به نام plum.csv ذخیره شدهاند. کد زیر به منظور ترسیم نموداری برای آشنایی بیشتر این دادهها نوشته شده است. متاسفانه دسترسی به فایل اطلاعاتی این دادهها امکان پذیر نبوده است. بنابراین امکان معرفی متغیرهای آن وجود ندارد به همین دلیل این فایل را فرضی نامیدیم.
1import pandas as pd
2import numpy as np
3import matplotlib.pyplot as plt
4
5# Absorbance data, collected in the matrix X
6X = np.log(1.0/pd.read_csv('./plums.csv').values)
7wl = np.arange(1100,2300,2)
8
9# Plot the data
10fig = plt.figure(figsize=(8,6))
11with plt.style.context(('ggplot')):
12 plt.plot(wl, X.T)
13 plt.xlabel('Wavelength (nm)')
14 plt.ylabel('Absorbance spectra')
15 plt.show()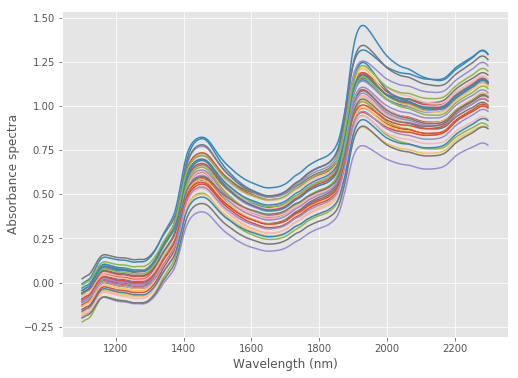
حال به کمک تفکیک یا تحلیل مولفههای اصلی (PCA)، مولفههای جدیدی را ایجاد میکنیم. همچنین به کمک نمودار score plot تشخیص میدهیم که ارتباط بین مولفه اول و دوم به چه شکل است. البته انتظار داریم که مولفههای تشکیل شده توسط PCA مستقل از یکدیگر باشند. این نمودار نیز چنین وضعیتی را به خوبی نشان میدهد.
1from sklearn.decomposition import PCA
2from sklearn.preprocessing import StandardScaler
3
4# Define the PCA object
5pca = PCA()
6
7# Run PCA on scaled data and obtain the scores array
8T = pca.fit_transform(StandardScaler().fit_transform(X))
9
10# Score plot of the first 2 PC
11fig = plt.figure(figsize=(8,6))
12with plt.style.context(('ggplot')):
13 plt.scatter(T[:, 0], T[:, 1], edgecolors='k', cmap='jet')
14 plt.xlabel('PC1')
15 plt.ylabel('PC2')
16 plt.title('Score Plot')
17plt.show()حاصل از اجرای این برنامه نمودار مولفهها است که در زیر میبینید.
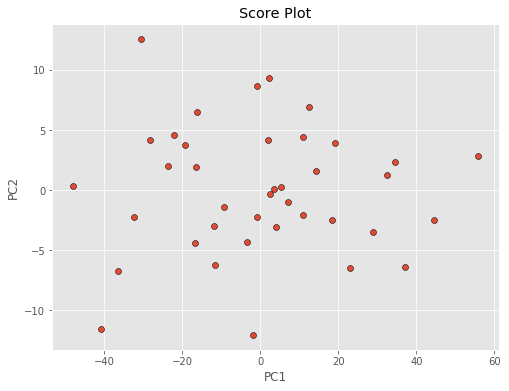
با توجه به نمودار ترسیم شده قبلی برای مولفهها، مشخص است که مولفه اول (PC1) دارای تغییرات در بازه 40- تا 60 است. در حالیکه میزان تغییرات (دامنه تغییرات) مولفه دوم (PC2) در فاصله ۱۲- تا ۱۲ قرار گرفته است.
حال اگر نمودار مولفههای را با یک مقیاس واحد ترسیم کنیم به نموداری مانند زیر خواهیم رسید.
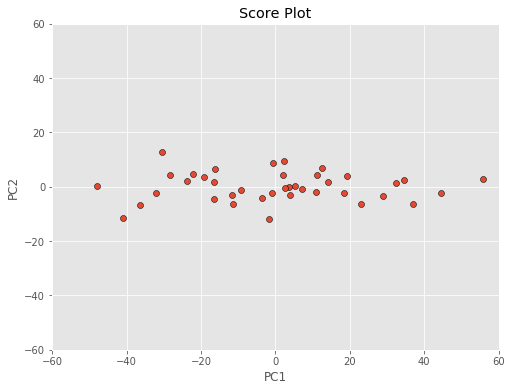
البته توجه داشته باشید که برای ترسیم این نمودار از کد زیر استفاده کردهایم.
1fig = plt.figure(figsize=(8,6))
2with plt.style.context(('ggplot')):
3 plt.scatter(T[:, 0], T[:, 1], edgecolors='k', cmap='jet')
4 plt.xlim((-60, 60))
5 plt.ylim((-60, 60))
6 plt.xlabel('PC1')
7 plt.ylabel('PC2')
8 plt.title('Score Plot')
9plt.show()مشخص است که تغییرات روی محور افقی بیشتر از محور عمودی است. بنابراین PC1 سهمی بیشتری در تفسیر تغییرات دادهها دارد. البته شاید این امر ناشی از واحد اندازهگیری متغیرهای مربوط به محور افقی یا مولفه اول باشد. با استفاده از چندین روش استاندارد یا نرمالسازی میتوان دادهها مقیاس دادهها را یکسان کرد. عمولا توزیع دادها (بخصوص داده با توزیع نرمال) را به کمک میانگین و واریانس (انحراف معیار) توزیع نشان میدهیم. به این ترتیب اگر Z را مقدار فاصله استاندارد شده نقطه x از توزیع در نظر بگیریم رابطه زیر را خواهیم داشت.
$$\large Z =\dfrac{(x-\mu)}{\sigma}$$
در این رابطه منظور از $$\mu$$ میانگین و $$\sigma$$ نیز انحراف معیار توزیع است. با استفاده از این کار میتوان مولفههای اصلی را استاندارد کرده و مقیاس محورها را یکسان کرد. به این ترتیب میزان تغییرات (واریانس یا انحراف معیار) روی هر دو محور برابر با ۱ خواهد بود.
در قسمت بعدی احتیاج به معیار یا اندازهای داریم که به کمک آن قادر به تشخیص نقاط پرت باشیم. در این نوشتار از «فاصله ماهالانوبیس» ( Mahalanobis Distance) استفاده میکنیم. البته قبل از استفاده از این تابع فاصله، محاسبات و تشخیص نقاط پرت را به کمک تابع فاصله اقلیدسی مرور کرده سپس به کمک فاصله ماهالانوبیس دادههای پرت را مورد بررسی قرار خواهیم داد.
فاصله اقلیدسی برای نمودار مولفههای اصلی
معمولا برای اندازهگیری فاصله، تابع فاصله اقلیدسی (Euclidean Distance) استفاده میشود. این تابع فاصله، تفسیر هندسی سادهای دارد. طول کوتاهترین خط مستقیم بین دو نقطه، همان فاصله اقلیدسی بین دو نقطه است. البته در حالت چند بعدی نیز همین خاصیت وجود دارد. در نمودار مولفهها (Score Plot) نیز کوتاهترین فاصله بین دو نقطه با فاصله اقلیدسی تعیین میشود.
بهتر است ابتدا یک تعریف از نقطه پرت ارائه دهیم. به نظر میرسد نقطه پرت، نقطهای است که از یک مقدارهای مربوط به یک توزیع خاص دور باشد. به این ترتیب احتیاج به اندازهگیری فاصله یک نقطه از یک توزیع داریم. معمولا توزیع دادها (بخصوص داده با توزیع نرمال) را به کمک میانگین و واریانس (انحراف معیار) توزیع نشان میدهیم. به این ترتیب اگر Z را مقدار فاصله استاندارد شده نقطه x از توزیع در نظر بگیریم، فاصله اقلیدسی بین نقطهها را براساس دادههای استاندارد شده ترسیم میکنیم. کدی که در زیر مشاهده میکنید به منظور محاسبه فاصله اقلیدسی براساس پنج مولفه اصلی نوشته شده است.
1# Compute the euclidean distance using the first 5 PC
2euclidean = np.zeros(X.shape[0])
3for i in range(5):
4 euclidean += (T[:,i] - np.mean(T[:,:5]))**2/np.var(T[:,:5])برای نمایش این فاصلهها روی نمودار ترسیم شده مولفهها از رنگهای مختلف استفاده کردهایم. هر چه نقطهها از مرکز دورتر باشند دارای تفکیک رنگ بیشتری خواهند شد. به این منظور کد زیر نوشته شده است.
1colors = [plt.cm.jet(float(i)/max(euclidean)) for i in euclidean]
2fig = plt.figure(figsize=(8,6))
3with plt.style.context(('ggplot')):
4 plt.scatter(T[:, 0], T[:, 1], c=colors, edgecolors='k', s=60)
5 plt.xlabel('PC1')
6 plt.ylabel('PC2')
7 plt.xlim((-60, 60))
8 plt.ylim((-60, 60))
9 plt.title('Score Plot')
10plt.show()پس از اجرای این کد نموداری به صورت زیر نمایش داده خواهد شد. مشخص است که نقطههایی که دور از مرکز هستند با رنگهای زرد و سبز و نارنجی و قرمز تیره مشخص شدهاند.
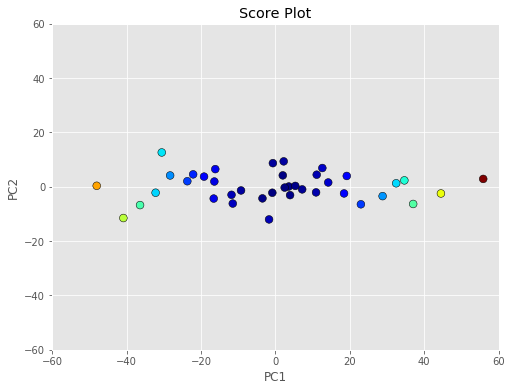
فاصله ماهالانوبیس برای نمودار مولفههای اصلی
دو مشکلی اساسی هنگام استفاده از فاصله اقلیدسی وجود دارد. مشکل اول ناشی از وجود رابطه یا همبستگی بین محورها است. اگر مقدارهای مربوط به محور افقی و عمودی با یکدیگر ارتباط یا همبستگی داشته باشند، فاصله اقلیدسی بزرگتر از حالتی است که مستقل باشند. به این ترتیب به نظر میرسد که فاصله اقلیدسی وزن بیشتری به مشاهدات مرتبط با هم میدهد. به این ترتیب اطلاع از مختصات یک نقطه میتواند در تعیین مختصات نقطه دیگر کمک کند و به این ترتیب آگاهی از مختصات یک نقطه میتواند برای جایگزین اطلاعات مربوط به نقطه دیگر باشد. در حالیکه در فاصله اقلیدسی درکی نسبت به این موضوع وجود ندارد و فاصلهها دوباره محاسبه شده و میتواند در مجموع، میانگین فاصلهها را تحت تاثیر قرار دهد. البته از آنجایی که متغیرها یا مولفههای مشخص شده در مولفههای اصلی مستقل از یکدیگر ایجاد میشوند، معمولا این مشکل در این حالت بروز نمیکند.
مشکل دوم و اساسی هنگام استفاده از فاصله اقلیدسی، محاسبه میانگین و انحراف استاندارد دادهها است. اگر واقعا مجموعه داده شامل نقاط پرت باشد، میانگین و انحراف استاندارد را تحت تاثیر خود قرار داده و محاسبات را دچار مشکل میکنند. توجه داشته باشید که دادههای پرت واقعا متعلق به توزیع اصلی دادهها نیستند. مقدارهای پرت ممکن است بر اثر خطای اندازهگیری یا موارد خاص بوجود آمده باشند که نمیتوانند گویای رفتار واقعی و دائمی پدیده تصادفی باشند. برای خروج از این بحران از فاصله ماهالانوبیس استفاده میکنیم. این تابع فاصله توسط چاندار ماهالانوبیس، دانشمند و آمار شناسی هندی در سال 1936 میلادی معرفی شد.

نحوه محاسبه فاصله ماهالانوبیس بسیار ساده است. اگر محورهای مربوط به مولفهها را با یک مقیاس واحد و واریانس ۱ ایجاد کنیم، فاصله اقلیدسی بین نقطهها، همان فاصله ماهالانوبیس خواهد بود. شیوه محاسبه آن برای برداری از نقطههای $${\displaystyle {x}=(x_{1},x_{2},x_{3},\dots ,x_{N})^{T}}$$ به صورت زیر است. در اینجا از نماد $$D_M$$ برای نمایش فاصله نقطه $$X$$ از توزیعی با بردار میانگین $$\mu$$ و ماتریس واریانس-کواریانس $$S^2$$ استفاده شده است.
$$\large {\displaystyle D_{M}({x})={\sqrt {({x}-{\mu })^{T}S^{-1}(x-{\mu })}}\,}$$
البته احتیاجی به دنبال کردن محاسبات نیست زیرا توابعی در کتابخانه scikit-learn محاسبه این تابع را در پایتون به عهده دارد. این کار به کمک برآوردگر پایدار ماتریس کوواریانس صورت میگیرد. کدی که در زیر مشاهده میکنید فاصله ماهالانوبیس برای مولفهها را محاسبه و نمودار را برحسب رنگهای مختلف که نشانگر فاصله است نشان میدهد.
1from sklearn.covariance import EmpiricalCovariance, MinCovDet
2
3# fit a Minimum Covariance Determinant (MCD) robust estimator to data
4robust_cov = MinCovDet().fit(T[:,:5])
5
6# Get the Mahalanobis distance
7m = robust_cov.mahalanobis(T[:,:5])همانطور که دیده میشود، نقاط پرت شناسایی شده توسط این روش، بیشتر از حالت قبل است.
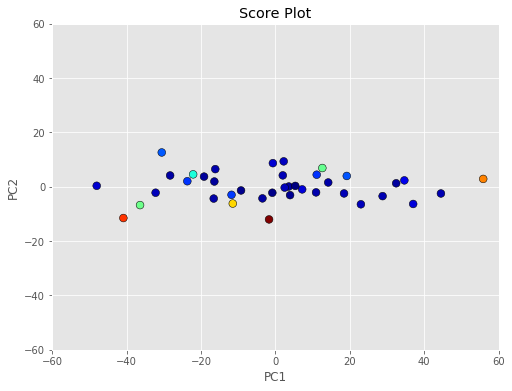
مشخص است که بعضی از نقاط که به نظر میرسد در مرکز قرار دارند، در این روش، نقطه پرت در نظر گرفته شدهاند.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزشهای آمار و احتمالات
- آموزش آماده سازی داده ها برای تحلیل آماری در SPSS
- مجموعه آموزشهای داده کاوی و یادگیری ماشین
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده
- تحلیل مولفه اساسی (PCA) در پایتون — راهنمای کاربردی
- استخراج (Extraction) و تبدیل (Transformation) داده ها در پایتون — راهنمای جامع











با سلام
وقت بخیر
مطلب برای من بسیار آموزنده بود
ما چنانچه از شما سوال داشته باشیم،چگونه میتوانیم مطرح کنیم؟
سلام وقت بخیر
میشه لطفاً فایل plum.csv را قرار دهید. ممنون
مسیر فایل csv
https://github.com/nevernervous78/nirpyresearch/blob/master/data/plums.csv
در ضمن برای رسم شکل آخر این کد رو اضافه کنید:
colors = [plt.cm.jet(float(i)/max(m)) for i in m]
fig = plt.figure(figsize=(8,6))
with plt.style.context((‘ggplot’)):
plt.scatter(T[:, 0], T[:, 1], c=colors, edgecolors=’k’, s=60)
plt.xlabel(‘PC1’)
plt.ylabel(‘PC2’)
plt.xlim((-60, 60))
plt.ylim((-60, 60))
plt.title(‘Score Plot’)
plt.show()
سلام و درود به شما خواننده مجله فرادرس.
متن مورد نظر شما ترجمهای از مجله علمی IDTOOLS است. در آن متن اشاره میکند که متاسفانه بنا به محرمانه بودن دادههای شرکت تولید کننده دستگاه، نمیتوانیم آنها را برای عموم ارائه کنیم. به همین دلیل ما هم به آن دادهها دسترسی نداریم و فقط با توجه به نمودارها و تشخیص روند تغییرات قادر به حدسهایی در مورد مقادیر واقعی هستیم.
از اینکه مطالب مجله فرادرس را دنبال میکنید بسیار خرسندیم.
شاد و تندرست و پیروز باشید.