انرژی فعالسازی (اکتیواسیون) — از صفر تا صد

در علوم شیمی و فیزیک، انرژی فعالسازی به انرژی میگویند که باید به یک سیستم شیمیایی یا هستهای شامل واکنشدهندههای بالقوه داده شود تا یک واکنش شیمیایی، هستهای یا پدیدههای مختلف فیزیکی رخ بدهند. انرژی فعالسازی را با $$E_a$$ نشان میدهند و واحد اندازهگیری آن، ژول $$(J)$$، کیلوژول بر مول $$(kJ/mol)$$ یا کیلوکالری بر مول $$(kcal/mol)$$ است.
مقدمه
تمامی مولکولها دارای یک مقدار حداقلی از انرژی هستند. این انرژی میتواند به صورت انرژی جنبشی یا پتانسیل باشد. زمانی که مولکولها با یکدیگر برخورد میکنند، انرژی جنبشی میتواند موجب کشش، خمش یا شکست پیوندها و به دنبال آن، انجام واکنش شیمیایی شود. اگر مولکولها با سرعت پایین و با انرژی جنبشی کمی حرکت کنند، یا اینکه با یکدیگر در جهتی مناسب برخورد نکنند، وارد واکنش نمیشوند و در اثر برخورد، تنها یکدیگر را دفع میکنند.
در هر صورت اگر مولکولها سرعت و جهت برخورد کافی داشته باشند، به گونهای که انرژی جنبشی به هنگام برخورد، بیش از حداقل انرژی مورد نیاز برای انجام واکنش باشد، در نهایت، واکنش مربوطه انجام خواهد شد. به این حداقل انرژی که برای انجام واکنش شیمیایی مورد نیاز است، انرژی فعالسازی (اکتیواسیون) میگویند.

توصیف ساده انرژی فعالسازی
در حقیقت، مسیری که یک واکنش شیمیایی طی میکند همانند تصویر بالا است. برای اینکه شئ به قله و بخش دیگر مسیر برسد باید سرعت مناسبی داشته باشد. هرقدر این سرعت بیشتر باشد، انرژی جنبشی بیشتری خواهیم داشت. اگر شئ با سرعت بسیار پایینی حرکت کند، انرژی جنبشی مناسبی برای رسیدن به قله نخواهد داشت و به قله نخواهد رسید. به همین شکل، یک مقدار حداقلی از انرژی باید وجود داشته باشد تا مولکولها بتوانند با شکستن پیوندهای خود، در یک واکنش شرکت کنند.
درصورتیکه انرژی جنبشی مولکولها در برخورد، بیش از حداقل انرژی مورد نیاز باشد، شکستن پیوندها و تشکیل پیوندهای جدید صورت میگیرد. البته این برخوردها باید جهت مناسبی نیز داشته باشند.
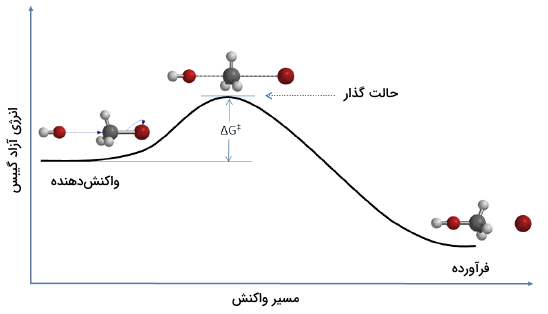
انرژی فعالسازی که در تصویر بالا با نماد $$\Delta{G^{\ddagger}}$$ نشان داده شده، اختلاف انرژی بین واکنشدهندهها و «کمپلکس فعال» (Activated Complex) است که این حالت را با نام «حالت گذار» (Transition State) نیز میشناسند. در یک واکنش شیمیایی، حالت گذار را به صورت بیشترین حالت انرژی در یک سیستم توصیف میکنند. اگر مولکولها در واکنشدهندهها با انرژی جنبشی مناسبی با یکدیگر برخورد کنند و این انرژی بیش از انرژی حالت گذار باشد، در نتیجه، واکنش انجام خواهد شد و فرآوردهها تشکیل میشوند. به عبارت دیگر، هرقدر انرژی فعالسازی بیشتر باشد، انجام یک واکنش، دشوارتر خواهد بود.
تاثیر آنزیم بر انرژی فعالسازی
درصورتیکه یک کاتالیست به واکنش اضافه شود، انرژی فعالسازی کاهش مییابد چراکه حالت گذار با انرژی پایینتری تشکیل خواهد شد. این آنزیمها، پروتئینها یا مولکولهای RNA هستند که مسیر جایگزینی با انرژی فعالسازی کمتر برای انجام واکنش فراهم میکنند. آنزیمها بر سرعت واکنش در هر دو مسیر رفت و برگشت تاثیرگذارند. سرعت این واکنشها به این دلیل افزایش مییابند زیرا مولکولها به هنگام برخورد، برای انجام واکنش به انرژی کمتری نیاز خواهند داشت. در نتیجه، ثابت سرعت $$(k)$$ افزایش خواهد یافت.
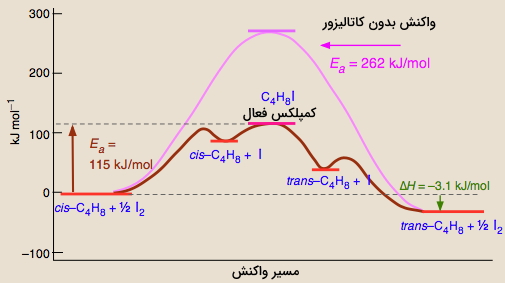
در واکنشهای بیولوژیکی، زمانی که یک آنزیم ( نوعی کاتالیزور) با یک سوبسترا پیوند تشکیل دهد، انرژی فعالسازی مورد نیاز کاهش پیدا میکند و به دنبال آن، سرعت واکنشهای رفت و برگشت افزایش مییابند. تصویر بالا، تاثیر کاتالیزور بر انرژی فعالسازی را نشان میدهد. لازم به ذکر است که کاتالیزورها فقط انرژی فعالسازی را کاهش نمیدهند بلکه مسیری به طور کامل متفاوت را برای انجام واکنش فراهم میکنند.
روابط بین آنتالپی، آنتروپی و انرژی آزاد گیبس
در ترمودینامیک، تغییرات انرژی آزاد گیبس $$(\Delta G )$$ را به صورت زیر تعریف میکنند:
رابطه (1): $$\Delta G = \Delta H - T \Delta S $$
$$\Delta G ^ o$$ را به صورت تغییر انرژی گیبس به هنگام انجام واکنش در شرایط استاندارد ذکر میکنند. برای محاسبه تغییرات انرژی آزاد گیبس در شرایطی به غیر از شرایط استاندارد، رابطه انرژی آزاد گیبس به صورت زیر خواهد بود:
رابطه (2): $$\Delta G = \Delta G ^ o + R T\ \ln K $$
- $$\Delta G$$: تغییرات انرژی گیبس واکنش
- $$\Delta G ^ o$$: انرژی آزاد گیبس استاندارد
- $$R$$: ثابت گازهای ایدهآل (ثابت جهانی گازها)
- $$K$$: ثابت تعادل
زمانی که واکنش در حال تعادل باشد، $$\Delta G = 0$$ و رابطه بالا به شکل زیر تبدیل میشود:
رابطه (۳): $$0 = \Delta G ^o + R T\ln K $$
رابطه (۴): $$\Delta G ^ o = -R T \ln K $$
به طور مشابه، در نظریه حالت گذار، انرژی فعالسازی گیبس را به صورت زیر تعریف میکنند:
رابطه (۵): $$\Delta G ^{\ddagger} = -RT \ln K^{\ddagger} $$
رابطه (۶): $$\Delta G ^{\ddagger} = \Delta H ^{\ddagger} - T \Delta S ^{\ddagger}$$
- $$\Delta G ^{\ddagger}$$: انرژی فعالسازی آزاد گیبس
- $$\Delta H ^{\ddagger}$$: آنتالپی فعالسازی
- $$\Delta S ^{\ddagger}$$: آنتروپی فعالسازی
با ترکیب معادلات ۵ و ۶ و حل آنها برای $$\ln K^{\ddagger}$$ به «رابطه ایرینگ» (Eyring Equation) خواهیم رسید:
رابطه (۷): $$\ln K^{\ddagger} = -\dfrac{\Delta H^{\ddagger}}{RT} + \dfrac{\Delta S^{\ddagger}}{R} $$
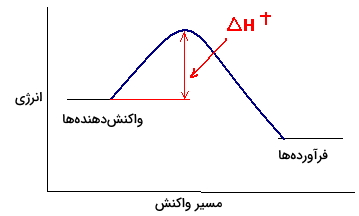
همانطور که در تصویر بالا دیده میشود، آنتالپی فعالسازی، بیانگر اختلاف انرژی بین حالت پایه و حالت گذار در یک واکنش شیمیایی است. توجه داشته باشید که مقدار آنتالپی فعالسازی، مشابه با مقدار انرژی فعالسازی $$E_a$$ است.
محاسبه انرژی فعالسازی به کمک معادله آرنیوس
بر اساس نظریه انرژی جنبشی گازها، با افزایش دما، سرعت مولکولهای گاز افزایش پیدا میکند. این مورد در خصوص مایعات و جامدات نیز صادق است.
انرژی جنبشی مولکولها با سرعت مولکولها طبق معادله زیر ارتباط دارد:
رابطه (۸): $$\mathrm{KE}=1 / 2 \mathrm{mv}^{2} $$
بنابراین، با افزایش دما، انرژی جنبشی نیز افزایش پیدا میکند. در نتیجه، کسری از مولکولها که انرژی جنبشی کافی برای غلبه بر حداقل انرژی دارند، افزایش مییابند. کسری از مولکولها که انرژی برابر یا بیشتر از $$E_a$$ دارند را با عبارت نمایی $$e^{\frac{- E _ a}{R T}}$$ در معادله زیر موسوم به معادله آرنیوس نشان میدهند:
رابطه (۹): $$k = A e^{\frac{-E _ a}{R T}} $$
- $$k$$: ثابت سرعت
- $$E_a$$: انرژی فعالسازی
- $$R$$: ثابت گازها
- $$T$$: دما بر حسب کلوین
- $$A$$: ثابت ضریب فرکانس که با نام «ضریب پیشنمایی» (Pre-exponential Factor) یا ضریب آرنیوس میشناسند. این عبارت سرعت برخورد و کسر برخوردهای موثر را نشان میدهد.
اگر از دو طرف رابطه بالا، لگاریتم طبیعی بگیریم، به رابطه زیر خواهیم رسید:
رابطه (10): $$\ln k = \ln A - \frac{E_a}{RT} $$
معادله بالا، شکلی خطی به صورت $$y = m x + b$$ دارد. رسم نمودار $$k$$ بر حسب $$1/T$$، خطی مستقیم با شیب $$- E _ a /R$$ و عرض از مبدا $$ln A$$ بدست میدهد. این نمودار در تصویر زیر نشان داده شده است:
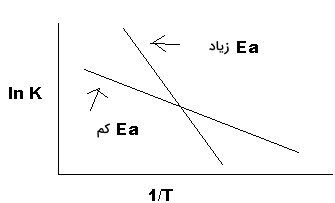
محاسبه انرژی فعالسازی به طور مستقیم
همانطور که در تصویر بالا دیده میشود، واکنشی با انرژی فعالسازی بیشتری، شیب تندی نیز دارد. در نتیجه، سرعت چنین واکنشی به تغییرات دما بسیار حساس است. در مقابل، واکنشی با انرژی فعالسازی کمتر، حساسیت کمتری نیز نسبت به دما دارد. از آنجایی که رادیکالها، به شدت واکنشپذیر هستند، انرژی فعالسازی برای این واکنشها برابر با صفر است.
همچنین، انرژی فعالسازی را میتوان به طور مستقیم با داشتن دما و ثابت سرعت در هر دما بدست آورد. با داشتن دماهای $$T_1$$ و $$T_2$$ و ثابتهای سرعت $$k_1$$ و $$k_2$$ خواهیم داشت:
رابطه (۱۱): $$\ln\; k_1 = - \frac{E_a}{RT_1} + \ln A $$
رابطه (۱۲): $$\ln\; k_2 = - \frac{E_a}{RT_2} + \ln A $$
اگر دو معادله بالا را از یکدیگر کم کنیم، به رابطه زیر میرسیم:
رابطه (۱۳): $$\ln\; k _ 1 - \ln\; k _ 2 = \left ( - \dfrac{E _ a}{R T _ 1} + \ln A \right ) - \left(- \dfrac{E _ a}{R T_ 2} + \ln A \right) $$
با بازآرایی رابطه، به معادلهای میرسیم که در آن، تنها با داشتن دو مقدار دما و ثابت سرعت، میتوانیم انرژی فعالسازی را محاسبه کنیم.
رابطه (۱۴): $$\ln \left (\dfrac{k_1}{k_2} \right ) = \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right)\dfrac{E_a}{R} $$
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای نرمافزارهای مهندسی شیمی
- آموزش الکتروشیمی کاربردی
- الکترون چیست؟ — به زبان ساده
- ساختار لوویس — به زبان ساده
^^