استنباط و آمار بیزی — به زبان ساده

معمولا در بین آماردانان دو سبک یا رویکرد برای «استنباط آماری» (Statistical Inference) وجود دارد که البته هر دو روش نیز امکان تجزیه و تحلیل دادهها را فراهم میآورد. در گروه اول که به گروه «فراوانیگراها» (Frequentists) مشهورند، پارامتر توزیع جامعه را مجهول ولی ثابت در نظر میگیرند در حالیکه در «رویکرد بیزی» (Bayesian Approach)، پارامتر نیز یک متغیر تصادفی در نظر گرفته شده که دارای توزیع خاص خود در فضای پارامتری است. در نتیجه استنباط آماری به دو دسته تقسیم میشود. دسته اول که با توجه به نظر فراوانیگراها پارامتر را مجهول ولی ثابت در نظر میگیرد. در نتیجه مفاهیمی مانند «تابع درستنمایی» (Likelihood Function)، «برآوردگر حداکثر درستنمایی» (Maximum Likelihood Estimator - MLE) و «آزمون نسبت درستنمایی» (Likelihood Ratio Test) که توسط دانشمند بزرگ آمار «رونالد فیشر» معرفی شد، مبنای استنباط آماری قرار میگیرد؛ از طرفی در دسته دوم که به دنبال استنباط و آمار بیزی هستند، مفاهیم توزیع پسین و پیشین با تابع درستنمایی ترکیب شده و برآوردگرها براساس «تابع زیان» (Loss Function) و محاسبه «تابع ریسک» (Risk Function) تعیین میشوند.
در این نوشتار به معرفی استنباط و آمار بیزی خواهیم پرداخت که البته بصورت مقدماتی بوده ولی میتوانید مباحث کامل و مفصل در این مورد را در ویدئو آموزش مقدماتی آمار بیزی مشاهده کنید. مباحث استنباط بیزی بیشتر با اصل یا قضیه بیز در ارتباط است. مطالب مربوط به این موضوع را در نوشتارهای قضیه بیز در احتمال شرطی و کاربردهای آن، احتمال شرطی و قضیه بیز در علم داده — راهنمای کاربردی و احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده میتوانید مطالعه کنید.
استنباط و آمار بیزی (Bayesian Inference)
اگر در مراحل انجام استنباط آماری، به اطلاعاتی که از قبل در مورد پارامتر مجهول جامعه داریم، توجه کرده و استنباط را، هم براساس نمونه تصادفی و هم اطلاعات پیشین پیریزی کنیم، استنباط بیزی انجام دادهایم. استنباط و آمار بیزی به کمک «قضیه بیز» (Bayesian Theorem) که روشی برای محاسبه احتمال شرطی است، عمل میکند.
به این ترتیب در استنباط بیزی، احتمال برای رخداد یک فرضیه را با توجه به شواهد و اطلاعات قبلی محاسبه کرده و سپس تصمیمسازی صورت میگیرد. امروزه از استنباط بیزی و قضیه بیز در بسیاری از رشتهها مانند علوم پزشکی و مهندسی استفاده میشود. برای مثال روش یا الگوریتم «دستهبند بیز ساده» (Naive Bayes Classifier) براساس قضیه بیز پایهریزی شده است.

استفاده از اطلاعات پیشین در استنباط آماری
همانطور که در قسمت قبل خواندید، مبنای استنباط و آمار بیزی، براساس «اطلاعات پیشین» (Prior Information) است که از پارامتر جامعه در اختیار داریم. به مجموعه این اطلاعات درباره پارامتر مجهول جامعه، «توزیع پیشین» (Prior Distribution) گفته میشود. در چنین مواقعی مجموعه مقادیری که پارامتر مجهول میتواند داشته باشد، فضای پارامتری میگویند و با نماد نشان میدهند. مشخص است که به این ترتیب پارامتر مجهول یکی از مقادیر خواهد بود.
از طرفی تصمیمهایی که قرار است به واسطه استنباط آماری یا تحلیل بیزی به آن دست بزنیم، «فضای عمل» (Action Space) نامیده میشود که آن را با نشان میدهند. برای اتخاذ تصمیم مناسب و ایجاد یک رابطه ترتیبی بین تصمیمها یا اعضای فضای عمل، برای هر عمل یک «مقدار زیان» (Loss Measure) در نظر میگیرند. به این ترتیب براساس میزان زیان، میتوان عملها را به ترتیب قرار داد و آنها را رتبهبندی کرد. به منظور درک بهتر این مفهومها و نحوه استفاده از اطلاعات پیشین در استنباط آماری به یک مثال میپردازیم.
مثال
فرض کنید سه کار یا عمل از مجموعه عملهای به صورت زیر موجود است.
فضای پارامتر یا نیز دارای دو عضو و است. میزان زیان برای هر یک از عملها با توجه به مقدار مختلف پارامتر، طبق جدول زیر دیده میشود.
| 3 | 6 | 2 | |
| 3 | 2 | 5 | |
همانطور که در جدول مشخص است براساس حداقل مقدار تابع زیان نمیتوان به عملی رسید که کمترین زیان را دارد. به نظر میرسد که عمل زمانی که پارامتر برابر با باشد بهتر ولی در زمانی که در وضعیت باشیم، عمل بهتر باشد. در نتیجه انتخاب عمل وابسته به مقدار است و نمیتوانیم تصمیم یا عملی را انتخاب کنیم که در همه حالات فضای پارامتری بهترین باشد.
در اینجا یکی از روشهای انتخاب مناسبترین (و البته نه بهترین) تصمیم میتواند تکیه به اطلاعات پیشین در میزان رخداد هر یک از مقدارهای مختلف فضای پارامتر و استفاده از استنباط و آمار بیزی باشد. روش دیگر انتخاب عملی است که از بین بیشترین میزان زیانها، کمترین باشد. به این قاعده تصمیمگیری، قاعده کمینهبیشینه (MiniMax) گفته میشود. بنابراین طبق مثال ما به نظر میرسد که عمل مناسبترین عمل با توجه به پارامترها باشد. به این روش تحلیل گاهی، «استنباط بدون داده» میگویند.
اصطلاحات اولیه در آمار و استنباط بیز
همانطور که در قبل اشاره شد، در استنباط و آمار بیزی برعکس استنباط کلاسیک (برمبنای فراوانی)، فضای پارامتر از متغیرهای تصادفی تشکیل شده است که خود دارای توزیع احتمالی هستند. در این میان علامتها و نمادهایی به کار گرفته میشوند که در زیر به صورت فهرستوار به آنها اشاره میکنیم.
- نقطه یا مشاهده که میتواند در حالت چند بُعدی به صورت یک بردار در نظر گرفته شود.
- پارامتر از توزیع آماری مورد نظر که یکی از نقاط فضای پارامتری یعنی است. بر این اساس مشخص است که است. ممکن است پارامتر توزیع به صورت برداری از پارامترها باشد. برای مثال در توزیع نرمال ممکن است میانگین و واریانس توزیع به عنوان بردار پارامتر توزیع در نظر گرفته شوند، یعنی باشد.
- «اَبَر پارامتر» (Hyperparameter) که پارامتر توزیع پارامتر مورد نظر است. در این حالت داریم . باز هم ممکن است که ابر پارامتر به صورت برداری باشد.
- مجموعه نمونه تصادفی که مقدارهای آن شامل مشاهده از است.
در ادامه به بررسی بعضی از اصطلاحات در زمینه استنباط و آمار بیزی خواهیم پرداخت.
توزیع پیشین
«توزیع پیشین» (Prior Distribution) در حقیقت همان توزیع پارامتر (پارامترهای) قبل از مشاهده نمونه تصادفی است. به این ترتیب میتوان آن را به صورت در نظر گرفت. انتخاب توزیع مناسب برای پارامتر توزیع، بستگی به نظر محقق و تجربه او و البته فضای پارامتر دارد.
مثال
فرض کنید که لازم است برای پارامتر واریانس توزیع نرمال ، برآوردی توسط استنباط بیزی تعیین شود، توزیع پیشین آن باید به شکلی باشد که تکیهگاه متغیر تصادفی توزیع پیشین، شامل مقدارهای منفی نباشد زیرا واریانس هرگز منفی نیست. بنابراین بهتر است مثلا از «توزیع کای ۲» (chi Square Distribution) یا «نرمال بریده شده» (Truncated Normal Distribution) استفاده کرد. حتی استفاده از یک توزیع یکنواخت (با دامنه مثبت) نیز میتواند مفید باشد.
مثال
برای یک توزیع دو جملهای با پارامتر معلوم و مجهول میخواهیم استنباط بیزی انجام دهیم. با توجه به فضای پارامتر که محدوده تغییرات آن در بازه است، انتخاب «توزیع بتا» (Beta Distribution) به عنوان توزیع پیشین مناسب به نظر میرسد.
نکته: اگر نتوان برای توزیع پیشین یک پارامتر، تابع توزیع خاصی را انتخاب کرد، بهتر است از توزیع بدون اطلاع یا توزیع «پیشین جفریز» (Jeffreys' Prior) که برحسب «اطلاع فیشر» (Fisher Information) محاسبه میشود، استفاده کرد.
توزیع نمونهای و تابع درستنمایی
«توزیع نمونهای» (Sampling Distribution) مربوط به توزیع نمونه تصادفی است که البته با شرط پارامتر نوشته میشود. به این ترتیب آن را به صورت نشان میدهیم تا نقش پارامتر مجهول را در محاسبه این تابع نشان دهیم. مشخص است که تابعی از پارامتر خواهد بود.
از آنجایی که این تابع چگالی برحسب متغیر دیده میشود، میتوان آن را همان تابع درستنمایی برای نمونه تصادفی در نظر گرفت. در این صورت میتوان رابطه زیر را برقرار دانست.
تابع درستنمایی حاشیهای
اگر نمونه تصادفی را به عنوان شواهد توزیع در نظر بگیریم میتوان تابع توزیع آن را به عنوان توزیع حاشیهای نسبت به پارامتر محاسبه کرد. در این حالت فرض کنید که متغیر تصادفی مربوط به نمونه تصادفی از توزیع مورد نظر باشد. در این صورت درستنمایی با توزیع حاشیهای برای به شکل زیر نوشته میشود.
به نظر میرسد که این توزیع به صورت امید ریاضی محاسبه شده است. البته توجه داشته باشید که در این محاسبه اَبَر پارامتر نیز حضور دارد.
توزیع پسین
«توزیع پسین» (Posterior Distribution)، توزیع پارامتر بعد از مشاهده نمونه تصادفی است. به این صورت به نظر میرسد که با توجه به شواهدی که از مشاهدات جمعآوری شده است، توزیع پیشین اصلاح شده و توزیع پسین بوجود خواهد آمد. رابطه بین توزیع پیشین و پسین به واسطه تابع درستنمایی و تابع درستنمایی حاشیهای حاصل میشود. طبق قضیه بیز این ارتباط به شکل زیر نوشته میشود.
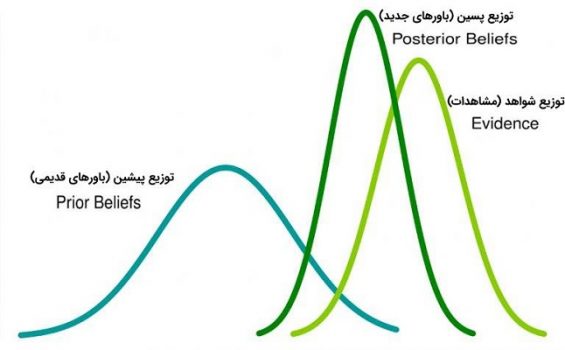
نکته: در انتهای رابطه مشخص است که از مخرج صرف نظر کردهایم، زیرا براساس مشاهده ثابت، مقدار آن تغییر نکرده و برای برآورد پارامتر و بیشینهسازی تابع پسین کافی است که صورت را حداکثر کنیم. از طرفی تابع احتمال برای اَبَر پارامتر نیز از صورت و مخرج ساده شده است و تاثیری در نتیجه نهایی ندارد.
خلاصه و جمعبندی
در بسیاری از شاخههای مهندسی و پزشکی، از استنباط و آمار بیزی استفاده میشود. برای مثال الگوریتمهای دستهبندی در «یادگیری ماشین نظارت شده» (Supervised Machine Learning) در هوش مصنوعی یا تخمین و محاسبه احتمال «منفی کاذب» (False Negative) در نتایج آزمایشهای پزشکی از کاربردهای آمار بیز و قضیه بیز محسوب میشوند. هر چند حوزه کاری در استنباط بیزی بسیار گسترده است، سعی کردیم در این متن کوتاه، خوانندگان را با مفاهیم اولیه و البته ضرورت استفاده از استنباط و آمار بیزی آشنا کنیم. برای آشنایی بیشتر و عمیقتر در این حوزه بهتر است به آموزش ویدئویی فرادرس با نام «آموزش مقدماتی آمار بیزی» مراجعه کنید.
اگر مطلب بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش مقدماتی آمار بیزی
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- قضیه بیز در احتمال شرطی و کاربردهای آن
- آموزش آمار و احتمال مهندسی
- احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
- تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
^^













سلام، متن خلاصه زیبایی بود ومن بعداز 44 سال فارغ التحصیل شدن در رشته آمارشناسی آن را فهمیده .لذت بسیار بردم، حال آنکه کمتر در رشته خود فعالیت داشته و بیشتر شغلم در زمینه مسئولیت شبکه های رایانه ای بوده است
با آرزوی بهروزی جهت همه پویندگان دانش