معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد

در مطالب قبلی وبلاگ فرادرس، مفاهیم پایه‌ای مکانیک سیالات مانند قوانین بقای جرم، معادلات پیوستگی و مومنتوم مورد بررسی قرار گرفتند. همانطور که اشاره شد در اکثر کاربردهای علم مکانیک سیالات مانند آیرودینامیک و توربوماشین‌ها، برای تحلیل میدان سرعتِ جریان سیال از معادلات ناویر-استوکس استفاده می‌شود. معادلات ناویر استوکس اولین بار در سال ۱۸۲۲ توسط «ناویر» (Claude-Louis Navier) بیان و بعدها توسط «استوکس» (George Gabriel Stokes) در حالات خاصی تکمیل شدند. البته روش‌هایی همچون تابع جریان نیز در سیالات وجود دارد که با استفاده از آن می‌توان به صورت تحلیلی یک جریان را تحلیل کرد.

ترکیب معادلات ناویر استوکس و معادله بقای جرم، مسئله مکانیک سیالات را خوش‌‌وضع می‌کند؛ یعنی تعداد مجهولات با تعداد معادلات برابر و حل مسئله به صورت تئوری امکان‌پذیر است. به صورت کلی می‌توان بیان کرد که معادلات ناویر استوکس یکی از مهم‌ترین معادلات مکانیک سیالات است که کاربرد زیادی در حل مسائل در علم دینامیک سیالات محاسباتی دارد. در این مطلب، مفاهیم و شیوه استخراج معادلات ناویر-استوکس به صورت قدم به قدم مورد مطالعه قرار می‌گیرند.

بقای مومنتوم خطی

برای توسعه فرم دیفرانسیلی معادلات مومنتوم ابتدا از معادله مومنتوم خطی شروع می‌کنیم که در بخش‌های قبل وبلاگ فرادرس به صورت کامل مورد بررسی قرار گرفت.

فیلم آموزش جریان لزج یا ویسکوز در فرادرس

کلیک کنید

این معادله را می‌توان به صورت زیر نمایش داد:

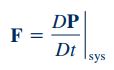
در رابطه بالا عبارت D()/Dt، عملگر مشتق مادی و F، نیروی وارد به جرم سیال را نمایش می‌دهند؛ همچنین P نشان‌دهنده مومنتوم خطی است که فرم انتگرالی آن برای یک سیستم به شکل زیر بیان می‌شود.

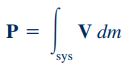
در مطلب مومنتوم خطی وبلاگ فرادرس، فرم انتگرالی معادله بالا برای یک حجم کنترل، به شکل زیر نشان داده شد.

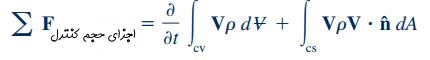
این معادله را می‌توان در یک حجم کنترل با اندازه محدود و برای حل بسیاری از مسائل مکانیک سیالات مورد استفاده قرار داد. برای به دست آوردن فرم دیفرانسیلی معادله مومنتوم خطی می‌توان روابط بالا را برای یک سیستم با جرم $$\delta m$$ بیان کرد. در این صورت رابطه ۳ به شکل زیر بازنویسی می‌شود.

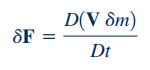
در معادله بالا $$\delta F$$، نیروی وارد بر جرم $$\delta m$$ را نشان می‌دهد. در این روش مقدار $$\delta m$$ را می‌توان به عنوان یک ثابت در نظر گرفت و رابطه ۴ را به فرم زیر بازنویسی کرد.

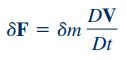
نکته دیگر این است که مشتق مادی سرعت (DV/Dt)، شتاب «المان» (Element) مورد نظر را نشان می‌دهد که با a نمایش داده می‌شود. بنابراین رابطه ۵ را به می‌توان به شکل زیر نشان داد.

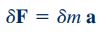
در واقع رابطه بالا به سادگی قانون دوم نیوتن را برای جرم $$\delta m$$ نشان می‌دهد. در واقع این معادله و معادله انتگرالی که در حجم کنترل نوشته می‌شود (رابطه ۳) نتایج یکسانی را در حل مسائل مکانیک سیالات تولید می‌کنند. یکی از مهمترین نکات در استفاده از معادله ۶، مشخص کردن $$\delta F$$ است. بنابراین در ادامه مطلب به بررسی روش‌های مختلف اعمال نیرو به جزئی دیفرانسیلی از یک سیستم پرداخته می‌شود. جز کوچک در این سیستم‌ها را اصطلاحا المان سیستم نیز می‌نامند.

توصیف نیروهای وارد بر جز دیفرانسیلی سیستم

برای استفاده از قانون دوم نیوتن برای یک سیستم به شکلی که در بالا نشان داده شد، به صورت کلی دو نوع مختلف نیرو را می‌توان در نظر گرفت. بخش اول نیروهای سطحی هستند که بر سطح یک المان دیفرانسیلی اعمال می‌شوند و بخش دوم نیروهای حجمی هستند که به صورت توزیعی از نیروها بر این المان وارد می‌شوند.

فیلم آموزش فراخوانی نرم افزار EES از متلب در فرادرس

کلیک کنید

نیروهای حجمی را با نماد $$\delta F_b$$ نشان می‌دهند. همچنین یکی از نیروهای حجمی که به جز کوچک سیال وارد می‌شود، وزن آن جز است که می‌توان رابطه آن را به شکل زیر نمایش داد.

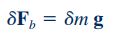
در این رابطه g بردار شتاب گرانش است. به منظور استفاده از یک بردار، در ابتدا بایستی آن را به اجزای سازنده‌اش تجزیه کرد. بنابراین شکل تجزیه‌شده رابطه ۷ به صورت زیر قابل بازنویسی است.

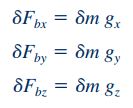
در سه رابطه بالا، $$g_y$$، $$g_x$$ و $$g_z$$ به ترتیب اجزای بردار شتاب گرانش در راستای x، y و z را نشان می‌دهند.

همانطور که بیان شد نیروهای دیگری نیز به نام نیروهای سطحی به یک جز دیفرانسیلی سیستم (المان سیستم) وارد می‌شوند. بر هم‌کنش این المانِ سیستم با محیط اطراف، نیروهای سطحی را تولید می‌کند.

نیروی سطحی وارد بر یک المان سیال با مساحت سطح $$\delta {A}$$ که در مکان دلخواهی از سیال قرار دارد، با علامت δF_s و مطابق با شکل زیر نشان داده می‌شود.

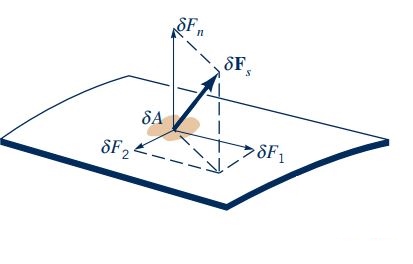
همانطور که در شکل بالا نشان داده شده، $$\delta {F_s}$$ از سه قسمت تشکیل می‌شود. قسمت اول $$\delta {F_n}$$ است که به صورت عمود بر سطح $$\delta {A}$$ وارد می‌شود. قسمت دوم و سوم یعنی $$\delta {F_1}$$ و $$\delta {F_2}$$ اجزایی از این نیرو هستند که به صورت موازی با سطح $$\delta {A}$$ قرار دارند و بر یکدیگر عمودند. بنابراین می‌توان «تنش عمودی» (Normal Stress) که بر این سطح وارد می‌شود را با استفاده از رابطه زیر محاسبه کرد.

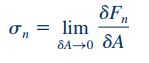
همچنین مشابه رابطه بالا می‌توان «تنش‌های برشی» (Shear Stresses) که در نتیجه اعمال نیروهای $$\delta {F_1}$$ و $$\delta {F_2}$$ بر سطح، تولید می‌شوند را به فرم زیر بیان کرد.

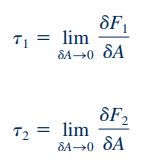
همانطور که در روابط بالا مشاهده می‌شود، عبارت $$\sigma$$ و $$\tau$$ به ترتیب برای نمایش تنش نرمال و تنش برشی استفاده شده‌اند. بنابراین در صورتی که مساحت و جهت یک جز سیستم مشخص باشد می‌توان نیرو بر واحد سطح را در این جز سیستم با استفاده از ترم‌های تنش برشی و تنش عمودی مشخص کرد. برای مثال یک سیستم مختصات را مشابه شکل زیر در نظر بگیرید.

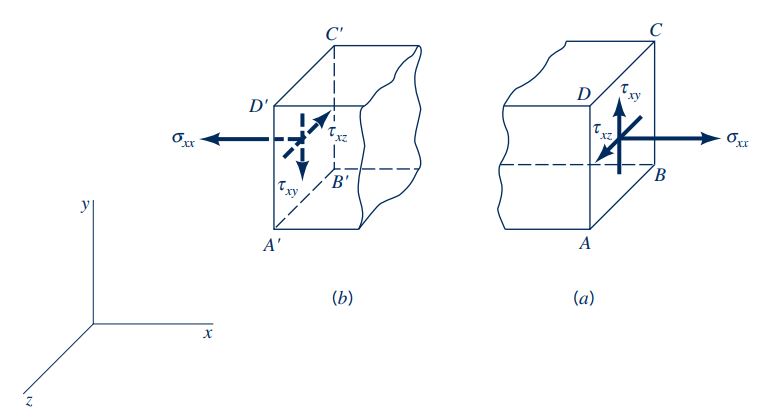
در این سیستم، تنش‌های عمودی و برشی در مختصات نمایش داده شده، نوشته می‌شوند. صفحه موازی با صفحه y-z (صفحه ABCD) را در نظر بگیرید. در این صفحه تنش عمودی با نماد $$\sigma_{xx}$$ و تنش‌های برشی با نمادهای $$\tau_{xy}$$ و $$\tau_{xz}$$ نشان داده شده‌اند.

مشابه مثال بالا در تمامی مسائل مکانیک سیالات برای مشخص کردن اجزای تنش از یک زیروند شامل دو حرف استفاده می‌شود. حرف اول، جهت بردار نرمال صفحه‌ای را نشان می‌دهد که تنش روی آن وارد شده است و حرف دوم جهت تنش را بیان می‌کند. نکته دیگر این است که زیروند تنش عمودی شامل دو حرف مشابه است در حالی که زیروند تنش برشی همواره شامل دو حرف متفاوت است.

علاوه بر نکته‌ای که در بالا برای نام‌گذاری تنش بیان شد، در اکثر مسائل مکانیک سیالات نیاز به تعریف یک قرارداد برای علامت این تنش داریم. در این مسائل مطابق شکل 1، در صورتی که بردار نرمال عمود بر سطح در جهت مثبت محورهای مختصات باشد، تنشی مثبت است که جهت آن در جهت مثبت محورهای مختصات باشد. این مورد در شکل بالا و قسمت (a) آن نشان داده شده است. در صورتی که جهت بردار عمود بر سطح به سمت منفی محورهای مختصات باشد، تنشی مثبت است که جهت بردار آن در خلاف جهت محورهای مختصات قرار داشته باشد. این موضوع در قسمت (b) شکل بالا به تصویر کشیده شده است. توجه کنید که مقدار مثبت تنش عمودی به حالتی گفته می‌شود که در آن، تنش به صورت کششی بر سیستم اعمال می‌گردد.

در ادامه به بررسی نیروهای سطحی می‌پردازیم که بر یک المان مکعبی از سیال وارد می‌شوند. این نیروها بر حسب تنش‌های وارد شده بر دیواره‌های المان، مطابق روابط موجود در شکل زیر قابل بیان هستند.

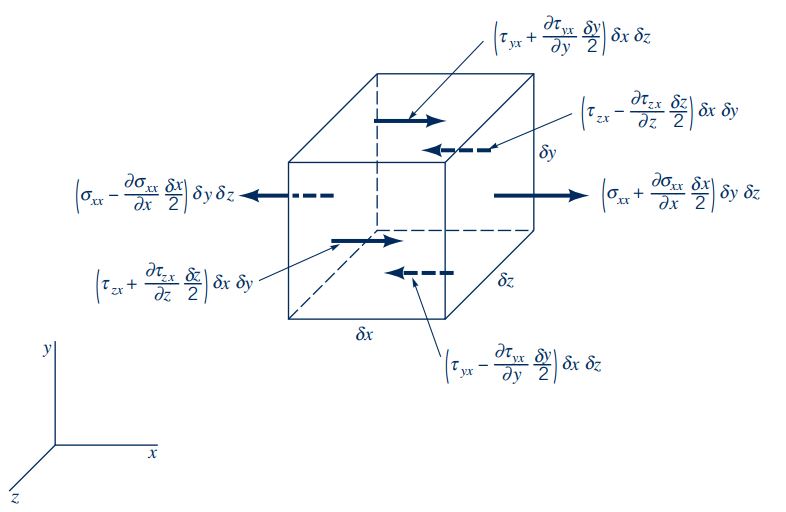
در مکانیک سیالات به صورت کلی می‌توان نشان داد که اندازه و جهت تنش‌ها در میدان جریان از نقطه‌ای به نقطه‌ دیگر متفاوت هستند. بنابراین برای استفاده از سری تیلور در این روابط، تنش‌های هر کدام از سطوح المان را بر حسب تنش موجود در مرکز المان شکل بالا و گرادیان آن در جهت محورهای مختصات بیان می‌کنیم. توجه شود که برای محاسبه نیرو باید تنش‌ها را در مساحت سطح ضرب کنیم. این موضوع در شکل بالا به خوبی نشان داده شده است.

برای محاسبه نیرو در راستای x باید تمام نیروهایی که در شکل بالا در راستای x نشان داده شده‌اند را با یکدیگر جمع کنیم. در نهایت نیروی سطحی وارد بر این المان در راستای x به شکل زیر در می‌آید.

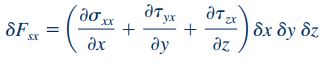
به طور مشابه برای محاسبه نیرو در راستای y و z نیز مانند رابطه بالا عمل می‌کنیم و حاصل جمع تمام نیروهای نشان داده شده در المان مکعبی در راستاهای مورد نظر را به دست می‌آوریم. در نهایت نیروهای سطحی در راستای y و z به شکل زیر در می‌آیند.

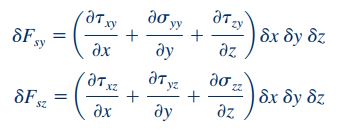
نیروی سطحی کلی که به المان سیستم وارد می‌شود ($$\delta {F_s}$$)، برابر با حاصل جمع برداری نیروی سطحی در سه راستای y، x و z است که در رابطه زیر به بررسی این موضوع پرداخته می‌شود.

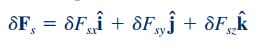
در نهایت برای استفاده از قانون مومنتوم خطی به محاسبه نیروی کلی وارد بر المان سیستم نیاز داریم. برای محاسبه نیروی کلی که با نماد $$\delta F$$ نشان داده می‌شود، باید رابطه بالا که نشان دهنده نیروی سطحی است با رابطه نیروی حجمی ($$\delta {F_b}$$) به صورت زیر جمع شوند.

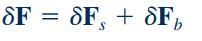
معادلات حرکت

در ادامه برای به دست آوردن معادلات حرکت، نیروهای سطحی و حجمی را در رابطه قانون دوم نیوتن وارد می‌کنیم. قانون دوم نیوتن برای یک المان سیال به جرم $$\delta {m}$$ به شکل زیر نمایش داده می‌شود.

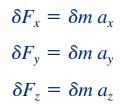
همچنین شتاب در مطلب سینماتیک سیالات با استفاده از رابطه زیر نمایش داده شد.

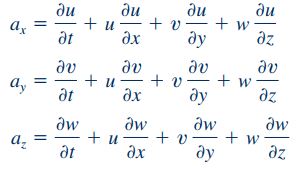
جرم المان سیال در این رابطه را می‌توان با استفاده از چگالی و حجم المان به شکل زیر محاسبه کرد.

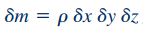
در نهایت با جایگذاری رابطه جرم و نیروها در قانون دوم نیوتن، فرم کلی معادله دیفرانسیلی حرکت در سیالات به شکل زیر در می‌آید.

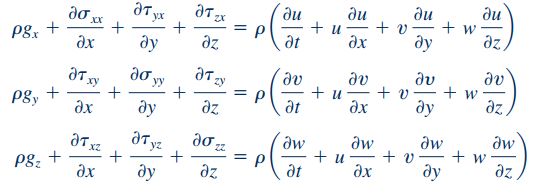
جریان لزج و معادلات ناویر استوکس

با بررسی دقیق معادله‌‌های دیفرانسیلی حرکت که در قسمت قبل بیان شد، به این نتیجه می‌رسیم که تعداد مجهولات موجود در این معادلات بیشتر از تعداد خود معادلات هستند. بنابراین به کمک این سه معادله نمی‌توان مجهولات مسئله را محاسبه کرد و برای برطرف کردن این موضوع باید رابطه‌ای بین سرعت سیال و تنش وارد بر آن نوشته شود.

فیلم آموزش مکانیک سیالات ۱ در فرادرس

کلیک کنید

رابطه بین تنش و سرعت

برای سیالات نیوتنی و غیر قابل تراکم، تنش را می‌توان به صورت خطی بر حسب مشتق سرعت نوشت. رابطه بین تنش عمودی و مشتق‌های سرعت در مختصات کارتزین به شکل زیر نمایش داده می‌شود.

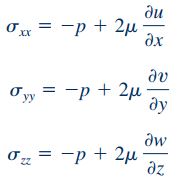
همچنین رابطه بین تنش‌های برشی و مشتق‌های سرعت در مختصات کارتزین به صورت زیر است.

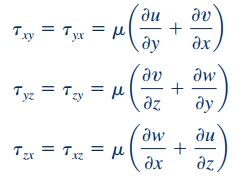
در این رابطه P فشار است که می‌توان آن را با استفاده از رابطه موجود در شکل زیر تعریف کرد.

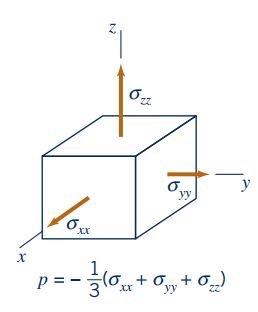
برای سیالات لزج، تنش عمودی در سه راستای y، x و z ضرورتاً یکسان نیستند؛ بنابراین نیاز هست که فشار را به صورت میانگین تنش عمودی در سه راستای مختلف به شکل بالا بیان کنیم. برای سیالات غیر لزج تنش عمودی در سه راستا با یکدیگر برابر هستند که روابط آن در بخش استاتیک سیالات بیان شد.

معادلات ناویر-استوکس

رابطه‌ بین تنش‌های مختلف و مشتق‌های سرعت در بخش قبلی بیان شد. در ادامه این رابطه را در معادله کلی حرکت بیان شده در قسمت قبل، جایگذاری می‌کنیم. فرم نهایی این معادلات به ترتیب در سه راستای y، x و z به شکل زیر نشان داده می‌شود.

در این روابط v، u و w به ترتیب سرعت در راستای y، x و z را مطابق شکل زیر نشان می‌دهند.

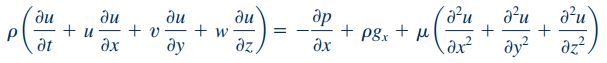
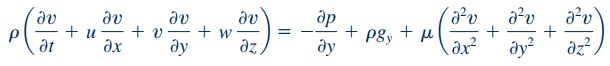
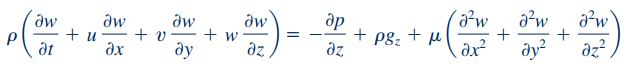
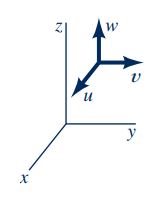
معادلات بالا به گونه‌ای نوشته شده‌اند که شتاب در سمت چپ و نیروهای وارده در سمت راست معادله موجود باشند. این معادلات تحت عنوان معادلات «ناویر-استوکس» (Navier-Stokes) شناخته می‌شوند.

در صورتی که این سه معادله با معادله بقای جرم ترکیب شوند، توصیف کاملی از ویژگی‌های مختلف میدان جریان یک سیال نیوتنی و غیر قابل تراکم را می‌توانند در اختیار ما قرار دهند. در واقع در اینجا ما ۴ معادله (۳ رابطه ناویر-استوکس و ۱ رابطه بقای جرم) و ۴ مجهول (سرعت در راستای y، x و z و فشار P) داریم؛ بنابراین به این مسئله اصطلاحاً «خوش وضع» (well-posed) گفته می‌شود. در مسائل خوش وضع تعداد معادلات و مجهولات با یکدیگر برابر هستند.

این معادلات با توجه به حضور ترم‌های غیر خطی در آن، به غیر از چند حالت خاص دارای حل ریاضی دقیق نیستند و برای حل آن‌ها از روش‌های عددی موجود در علم دینامیک سیالات محاسباتی مانند روش تفاضل محدود و روش حجم محدود استفاده می‌شود. نتایج این معادلات در حالات مختلف با نتایج آزمایش‌های تجربی مقایسه شدند و تطابق خوبی بین نتایج آزمایش‌های تجربی و معادلات ناویر-استوکس نشان داده شده است. بنابراین معادلات ناویر استوکس به شکل بالا را می‌توان به عنوان معادلات دیفرانسیلی حاکم بر سیال‌های نیوتنی غیر قابل تراکم بیان کرد.

در این مطلب ابتدا به صورت جامع به شیوه محاسبه معادلات حرکت در مکانیک سیالات پرداخته شد و در نهایت با استفاده از رابطه تنش و سرعت در سیالات لزج، معادلات ناویر استوکس به دست آمدند. این معادلات در حالات خاص مانند «جریان کوئت» (Couette Flow)، «جریان پوازی» (Poiseuille Flow)، جریان پایا و لایه‌ای بین دو صفحه موازی یا لوله‌های دایروی، دارای حل دقیق ریاضی هستند. معادلات ناویر استوکس نقش اساسی در علم دینامیک سیالات محاسباتی برای تحلیل عددی جریان سیال بازی می‌کند و کاربرد آن در علوم آیرودینامیک و توربوماشین مشهود است.

در صورتی که به مطلب ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• دینامیک سیالات محاسباتی (CFD) — از صفر تا صد
• آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
• تابع جریان در سیالات -- به زبان ساده
• سیال غیر نیوتنی (Non Newtonian Fluid) — از صفر تا صد
• ممنتوم زاویه‌ای (Moment of Momentum) در سیالات — آموزش سریع و ساده
• توربوماشین (Turbomachinery) — به زبان ساده

^^