جریان پوازی (Poiseuille Flow) — به زبان ساده

همانطور که در مطالب قبلی وبلاگ فرادرس بیان شد، معادلات ناویر استوکس، در برخی از حالات خاص، مانند جریان کوئت، جریان پوازی و ... جواب دقیق دارند. مفاهیم و روابط حاکم بر جریان کوئت در مطالب قبلی به صورت دقیق مورد بررسی قرار گرفتند. حالت دیگری که معادلات ناویر استوکس در آن جواب دقیق دارند، حالتی است که سیال درون یک لوله‌ دایروی مستقیم با سطح مقطع یکنواخت، به صورت پایا، غیر قابل تراکم و لایه‌ای، جریان دارد. این نوع خاص از جریان را «جریان هاگن-پوازی»‌ (Hagen–Poiseuille Flow) و یا به صورت ساده شده، «جریان پوازی» (Poiseuille Flow) می‌نامند.

علت نام گذاری جریان هاگن پوازی به این نام، تحقیقات فراوان دانشمند فرانسوی به نام لئونارد پوازی با نام کامل Jean Léonard Marie Poiseuille و دانشمند آلمانی به نام هنریش هاگن و با نام کامل Gotthilf Heinrich Ludwig Hagen در زمینه جریان درون لوله‌ها است. این مطلب در ابتدا به بررسی مفهوم جریان هاگن پوازی و روابط حاکم بر آن می‌پردازد و در انتهای مطلب نیز، کاربرد این رابطه برای محاسبه ویسکوزیته سیالات مورد بررسی قرار می‌گیرد.

جریان هاگن-پوازی

پوازی به جریان خون درون مویرگ‌ها، علاقه بسیار زیادی داشت و موفق شد به صورت آزمایشگاهی، مقاومت سیال در جریان لایه‌ای گذرنده از لوله دایروی را مشاهده کند. هاگن نیز به صورت آزمایشگاهی به مطالعه جریان در لوله‌ها پرداخت. در واقع نتایج تئوری که در این مطلب به بیان آن‌ها پرداخته می‌شود، بعد از مطالعات هاگن و پوازی به دست آمده‌اند، با این حال این جریان خاص، به صورت رایج به نام این دو دانشمند شهرت دارد.

فیلم آموزش مکانیک سیالات ۱ در فرادرس

کلیک کنید

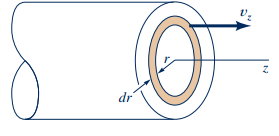
سیالی را در نظر بگیرید که مطابق شکل زیر، درون یک لوله دایروی افقی با سطح مقطع یکنواخت به شعاع R، در حال عبور است و جریان سیال در آن به صورت پایا، غیر قابل تراکم و لایه‌ای، فرض می‌شود. در ادامه، پاسخ معادلات ناویر-استوکس در این جریان خاص، مورد بررسی قرار گرفته‌ است.

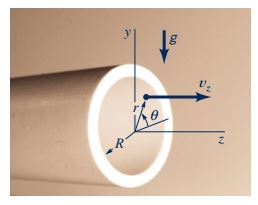
از آنجایی که هندسه نشان داده شده، به صورت یک لوله استوانه‌ای است، از دستگاه مختصات استوانه‌ای نیز برای تحلیل جریان درون آن استفاده می‌شود. در این حالت، جریان به صورت موازی با سطوح جانبی استوانه در نظر گرفته می‌شود بنابراین می‌توان فرض کرد که مطابق روابط زیر، سرعت در راستای r و θ برابر با صفر هستند.

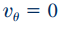
در ادامه، معادله پیوستگی را برای این سیال به شکل زیر در مختصات استوانه‌ای می‌نویسیم.

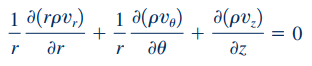
در صورتی که روابط ۱ و ۲ در رابطه ۳ جایگذاری شوند، عبارت زیر برای سرعت در راستای محور لوله محاسبه می‌شود.

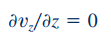
نکته دیگری که باید به آن اشاره کرد، این است که، سرعت محوری یک نقطه از سیال در جریان متقارن پایا، تابعی از t و θ نیست. بنابراین با توجه به نکات ذکر شده و رابطه ۴، می‌توان نتیجه گرفت که سرعت محوری در این نقطه (v_z) تنها تابعی از فاصله این نقطه از مرکز لوله است.

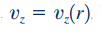
معادلات ناویر-استوکس برای این جریان خاص، به شکل زیر قابل بازنویسی هستند.

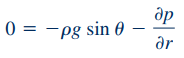
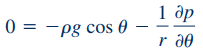
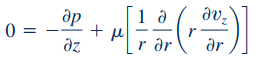
برای محاسبه روابط بالا، شتاب گرانش در راستای r و θ در معادلات اصلی ناویر-استوکس، به شکل زیر جایگذاری شده‌اند.

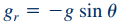
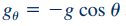
همانطور که در شکل ۱ نشان داده شده، زاویه θ نسبت به سطح افقی محاسبه می‌شود. در ادامه با ترکیب معادلات ۶ و ۷ رابطه زیر برای فشار به دست می‌آید.

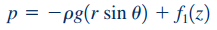
این رابطه را می‌توان به فرم زیر نمایش داد.

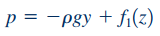
رابطه ۱۲ نشان می‌دهد که فشار در یک مقطع خاص از این لوله، به صورت هیدرواستاتیک توزیع شده است. نکته دیگر این است که گرادیان فشار در راستای z تابعی از r و θ نیست. بر این اساس، معادله حرکت در راستای z (رابطه 8) را می‌توان به شکل زیر بازنویسی کرد.

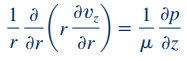
در ادامه، از طرفین رابطه بالا انتگرال می‌گیریم. نکته‌ای که باید به آن توجه کرد این است که گرادیان فشار در راستای z، تابعی از r و θ نیست. بنابراین در این انتگرال‌گیری، سمت راست معادله به فرم یک ثابت در نظر گرفته می‌شود.

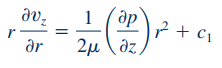
از طرفین معادله بالا یک بار دیگر به شکل زیر انتگرال می‌گیریم.

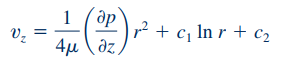
همانطور که در رابطه بالا مشاهده می‌شود، شکل پروفیل سرعت به مقادیر پارامترهای c₁ و c₂ بستگی دارد. این موضوع در شکل زیر به تصویر کشیده شده است.

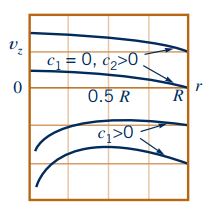
در جریان مورد مطالعه، انتظار داریم که اندازه سرعت در راستای z و در مرکز لوله، مقداری محدود داشته باشد. همچنین می‌دانیم که لگاریتم صفر برابر با منفی بینهایت می‌شود. بنابراین ضریب عبارت لگاریتمی در رابطه 15 یعنی c₁ برابر با صفر است.

ضریب c₂ نیز با توجه به این نکته محاسبه می‌شود که سرعت در دیواره (r = R) برابر با صفر است.

بنابراین رابطه 15 که سرعت محوری را نشان می‌دهد به شکل زیر بازنویسی می‌شود.

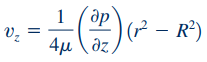
همانطور که مشاهده می‌شود، توزیع سرعت در تمام سطح مقطع‌ها، به فرم سهموی است. در ادامه به محاسبه دبی حجمی سیال (Q) عبوری از لوله و گرادیان فشار پرداخته می‌شود. برای این منظور، یک مقطع دیفرانسیلی مورد نیاز است که می‌توان آن را مطابق با شکل ۲ به صورت یک واشر در نظر گرفت.

همانطور که در قسمت قبل نیز نشان داده شد، سرعت محوری سیال در این لوله، تنها به شعاع مقطع بستگی دارد. بنابراین سرعت محوری در تمام نقاط این مقطع دیفرانسیلی که در شکل ۲ نشان داده شده، یکسان در نظر گرفته می‌شود. همچنین می‌توان دبی حجمی سیال عبوری از این سطح مقطع دیفرانسیلی را با استفاده از رابطه زیر محاسبه کرد.

بنابراین همانطور که توضیح داده شد، با انتگرال‌گیری از رابطه فوق، دبی حجمی کلی سیال عبوری از این مقطع لوله به شکل زیر محاسبه می‌شود.

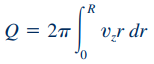
در ادامه، ابتدا رابطه ۱۷ را در معادله فوق، جایگذاری می‌کنیم و سپس انتگرال‌گیری را روی شعاع مقاطع دیفرانسیلی مختلف انجام می‌دهیم. در نهایت این رابطه به شکل زیر در می‌آید.

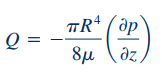
معادله بالا را می‌توان بر حسب افت فشار لوله (ΔP) نیز بازنویسی کرد. این افت فشار در طول لوله رخ می‌دهد و به صورت آزمایشگاهی قابل اندازه‌گیری است. رابطه افت فشار در طول لوله با گرادیان فشار در راستای z، به شکل زیر بیان می‌شود.

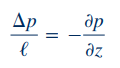
بنابراین رابطه 20 برای دبی حجمی کلی سیال، به شکل زیر بازنویسی می‌شود.

فیلم آموزش مقدماتی مکانیک سیالات ۲ در فرادرس

کلیک کنید

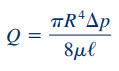
همانطور که مشاهده می‌شود برای یک لوله با افت فشار مشخص در طول آن، مقدار دبی حجمی با ویسکوزیته سیال رابطه عکس و با توان چهارم شعاع لوله رابطه مستقیم دارد. بنابراین می‌توان نتیجه گرفت که با دو برابر کردن شعاع لوله، دبی عبوری از آن 16 برابر می‌شود. رابطه ۲۲ به صورت رایج با نام «قانون پوازی» (Poiseuille’s Law) شناخته می‌شود.

با استفاده از رابطه بالا، سرعت متوسط سیال در این لوله به شکل زیر قابل محاسبه است.

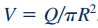
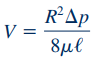
نکته دیگر این است که با توجه به رابطه 17، ماکزیمم سرعت در مرکز لوله رخ می‌دهد و مقدار این سرعت ماکزیمم با استفاده از رابطه زیر قابل محاسبه است.

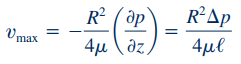
همانطور که مشاهده می‌شود مقدار سرعت ماکزیمم دو برابر مقدار سرعت میانگین سیال در این لوله است و رابطه زیر را می‌توان بین سرعت میانگین و سرعت ماکزیمم نمایش داد.

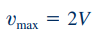
توزیع سرعت در این لوله را می‌توان به کمک رابطه‌ای بر حسب سرعت ماکزیمم به شکل زیر بازنویسی کرد.

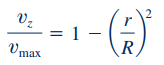
همانطور که مشاهده می‌شود سرعت در مرکز لوله، ماکزیمم است و در دیواره‌ها مقداری برابر با صفر دارد. این موضوع در شکل زیر به تصویر کشیده شده است.

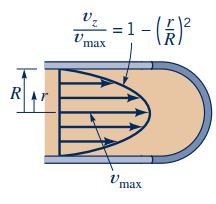
در مطالعات مختلف، نتایج آزمایشگاهی جریان درون لوله با نتایج تئوری مقایسه شده و درستی این روابط برای جریان لایه‌ای درون یک لوله به اثبات رسیده است. توجه کنید که این روابط برای جریان لایه‌ای بیان شده‌اند. می‌دانیم که جریان، در اعداد رینولدز کمتر از 2100 به صورت لایه‌ای باقی می‌ماند و عدد رینولدز در این مسائل به شکل زیر محاسبه می‌شود.

همانطور که در مطلب ویسکوزیته در وبلاگ فرادرس اشاره شد، یکی از کاربردهای معادله پوازی محاسبه ویسکوزیته سیال است. بنابراین در صورتی که ویسکوزیته سیال، مجهول باشد می‌توان آن را در یک لوله با شرایطی که در بالا توضیح داده شد به جریان دراورد و در نهایت ویسکوزیته این سیال را با استفاده از رابطه زیر محاسبه کرد. این رابطه از قانون پوازی‌ (رابطه ۲۲) استخراج شده است.

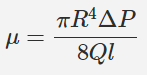
بنابراین در صورتی که شعاع و طول لوله معلوم باشد و بتوانیم افت فشار و دبی حجمی سیال عبوری از لوله را محاسبه کنیم، ویسکوزیته سیال طبق رابطه بالا قابل محاسبه است.

همانطور که اشاره شد، جریان پوازی به حالتی گفته می‌شود که در آن، سیال درون یک لوله‌ دایروی مستقیم با سطح مقطع یکنواخت به صورت پایا، غیر قابل تراکم و لایه‌ای، جریان دارد. این مطلب ابتدا به بررسی مفهوم جریان هاگن پوازی و روابط حاکم بر آن پرداخت و در ادامه کاربرد این رابطه برای محاسبه ویسکوزیته سیالات مختلف مورد بررسی قرار گرفت.

در صورتی که قصد یادگیری بیشتر در زمینه‌ مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• ویسکوزیته (Viscosity) — به زبان ساده
• جریان توسعه یافته (Fully Developed Flow) — به زبان ساده
• جریان کوئت (Couette Flow) در مکانیک سیالات — از صفر تا صد
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد

^^