مومنتوم زاویه ای (Moment of Momentum) در سیالات – آموزش سریع و ساده

همانطور که در مطالب قبلی وبلاگ فرادرس اشاره شد، قانون بقای جرم، معادله پیوستگی، مومنتوم خطی و مومنتوم زاویه‌ای، کاربرد بسیار زیادی در مکانیک سیالات و محاسبه میدان سرعت جریان دارند. معادلات مومنتوم خطی و مومنتوم زاویه‌ای به صورت کلی با توجه به قانون دوم نیوتن به دست می‌آیند. در مطالب قبلی، مومنتوم خطی و روابط حاکم بر آن بررسی شدند و شیوه کاربرد مفهوم مومنتوم خطی در مسائل مکانیک سیالات مورد بحث قرار گرفت. در این مطلب ابتدا مفهوم مومنتوم زاویه‌ای و روابط حاکم بر آن به صورت دقیق مورد بررسی قرار می‌گیرند و در انتهای مطلب به کمک یک مثال، کاربرد معادله مومنتوم زاویه‌ای در حل مسائل مکانیک سیالات نشان داده می‌شود.

معادله مومنتوم زاویه‌ای

در بسیاری از مسائل مهندسی، «گشتاور» (Torque) حول یک محور، مفهوم بسیار مهمی است که با استفاده از رابطه $$T=\overrightarrow {r} \times \overrightarrow {F}$$ محاسبه می‌شود. در این رابطه $$\overrightarrow {r}$$ بردار فاصله نیرو تا محور و $$\overrightarrow {F}$$ بردار نیرو را نشان می‌دهند. در مطلب «مومنتوم خطی در سیالات» برای محاسبه معادله مومنتوم خطی از قانون دوم نیوتن استفاده کردیم و به روابط قابل استفاده برای مسائل مکانیک سیالات دست یافتیم.

در این مطلب، هدف تعیین معادله مومنتوم زاویه‌ای است. این معادله را می‌توان با ضرب طرفین معادله مومنتوم خطی در فاصله نیرو از محور دوران محاسبه کرد. بنابراین برای شروع،‌ قانون دوم نیوتن برای یک ذره سیال را به فرم زیر می‌نویسم:

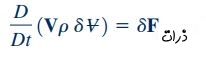
در این رابطه، V سرعت ذره سیال است که در یک سیستم مختصات لَخت محاسبه می‌شود. عبارت سمت راست رابطه بالا، نیروی خارجی که بر این ذره وارد می‌شود را نشان می‌دهد. در ادامه و برای محاسبه مومنتوم زاویه‌ای، گشتاور دو سمت رابطه فوق را نسبت به محور با فاصله r از آن، محاسبه می‌کنیم. برای این منظور، معادله بالا را به صورت ضرب خارجی r در دو طرف رابطه و به شکل زیر بازنویسی می‌کنیم.

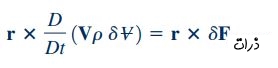
برای ساده‌سازی رابطه بالا نیاز به استفاده از روابط ریاضی و مفهوم ضرب خارجی داریم. یکی از ویژگی‌های ضرب خارجی در ریاضیات، در رابطه زیر نشان داده شده است.

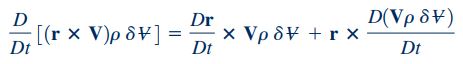
برای ساده‌سازی رابطه بالا از این نکته استفاده می‌کنیم که حاصل مشتق مادی r برابر با V می‌شود. بنابراین عبارت اول سمت راست رابطه فوق به صورت حاصل ضرب خارجی عبارت V در خودش در می‌آید که می‌توان آن را به فرم زیر نمایش داد.

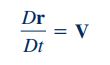
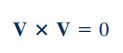
بنابراین در صورتی که روابط 3، 4 و 5 در رابطه 2 قرار داده شوند، معادله مومنتوم زاویه‌ای به فرم زیر بازنویسی می‌شود.

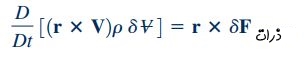
رابطه فوق برای تمام ذراتی که در یک سیستم حضور دارند، صادق است. بنابراین این رابطه را می‌توان برای کل سیستم بازنویسی کرد. برای این منظور باید مومنتوم زاویه‌ای سیستم، به صورت مجموع مومنتوم زاویه‌ای تک تک ذرات تشکیل دهنده آن سیستم نوشته شود که این کار با استفاده از رابطه انتگرالی زیر انجام می‌شود.

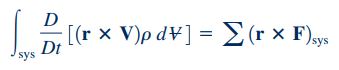
در مکانیک سیالات با توجه به تعاریف سیستم و مشتق مادی، روابط زیر برای ذرات یک سیستم و مشتق مادی آن سیستم برقرار هستند.

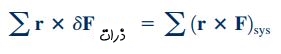
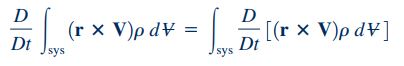
بنابراین با استفاده از روابط ۸ و ۹، در نهایت رابطه 7 به شکل زیر بازنویسی خواهد شد:

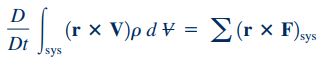
سمت چپ این معادله، نرخ زمانی تغییرات مومنتوم زاویه‌ای سیستم را نمایش می‌دهد و عبارت سمت راست این معادله نشان‌دهنده مجموع گشتاور نیروهای خارجی است که به سیستم وارد می‌شود. نکته مهم دیگر این است که، گشتاور وارد بر یک حجم کنترل که به سیستم چسبیده است با گشتاور وارد بر آن سیستم برابر است. رابطه ۱۱ به خوبی این موضوع را نشان می‌دهد. همچنین روش محاسبه گشتاور به صورت شماتیک در شکل زیر نمایش داده شده است.

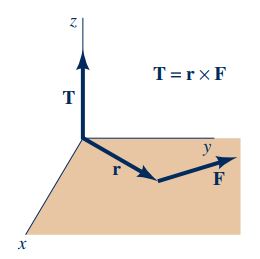
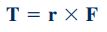
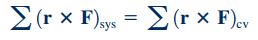
قدم بعدی برای به دست آوردن رابطه مومنتوم زاویه‌ای، محاسبه معادله انتقال رینولدز است. در سیستم نشان داده شده، حجم کنترل به صورت ثابت و چسبیده به سیستم انتخاب شده است و این حجم کنترل قابلیت تغییر شکل ندارد. برای چنین حجم کنترل و سیستمی رابطه انتقال رینولدز را می‌توان به شکل زیر نوشت.

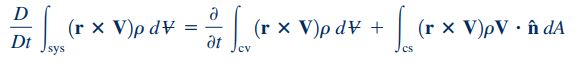
ترم سمت چپ معادله انتقال رینولدز نشان دهنده نرخ زمانی تغییرات مومنتوم زاویه‌ای یک سیستم است و به صورت مشتق مادی نمایش داده می‌شود. عبارت اول در سمت راست معادله بالا، نشان دهنده نرخ زمانی تغییرات مومنتوم زاویه‌ای برای حجم کنترل است و عبارت دوم سمت راست معادله فوق، نرخ مومنتوم زاویه‌ای خالص عبوری از مرزهای حجم کنترل است.

در ادامه برای این حجم کنترل که ساکن است و تغییر شکلی در آن رخ نمی‌دهد، روابط 10، 11 و 12 را با یکدیگر ترکیب می‌کنیم و در نهایت معادله مومنتوم زاویه‌ای را به شکل زیر می‌نویسیم.

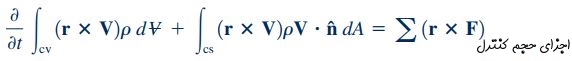
کاربرد معادله مومنتوم زاویه‌ای در حل مسائل

معادله مومنتوم زاویه‌ای که در این بخش به بررسی آن پرداخته شد، در حل مسائل مربوط به ماشین‌های چرخان مانند توربوماشین‌ها، پره‌های توربین و کمپرسور و آب‌پاش‌های چمن به صورت رایج مورد استفاده قرار می‌گیرد. در هرکدام از مسائل با توجه به شرایط خاص آن مسئله، معادله مومنتوم زاویه‌ای به شکل‌های مختلف اصلاح می‌شود.

در برخی از مسائل برای ساده‌سازی حل، جریان به صورت یک بعدی در نظر گرفته می‌شود. در این حالت توزیع یکنواختی از سرعت متوسط در هر بخش جریان موجود است و ضرب خارجی موجود در رابطه مومنتوم زاویه‌ای (رابطه 13) به صورت ساده قابل محاسبه است.

در گروهی دیگر از مسائل مکانیک سیالات برای ساده‌سازی معادله مومنتوم زاویه‌ای، جریان به صورت پایا در نظر گرفته می‌شود. در این حالت عبارت اول سمت چپ معادله مومنتوم زاویه‌ای به شکل زیر نوشته می‌شود و برابر با صفر است.

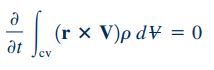
برای بررسی بیشتر کاربرد معادله مومنتوم زاویه‌ای در مسائل مکانیک سیالات، یک آب‌پاش چرخان را مطابق شکل زیر در نظر بگیرید.

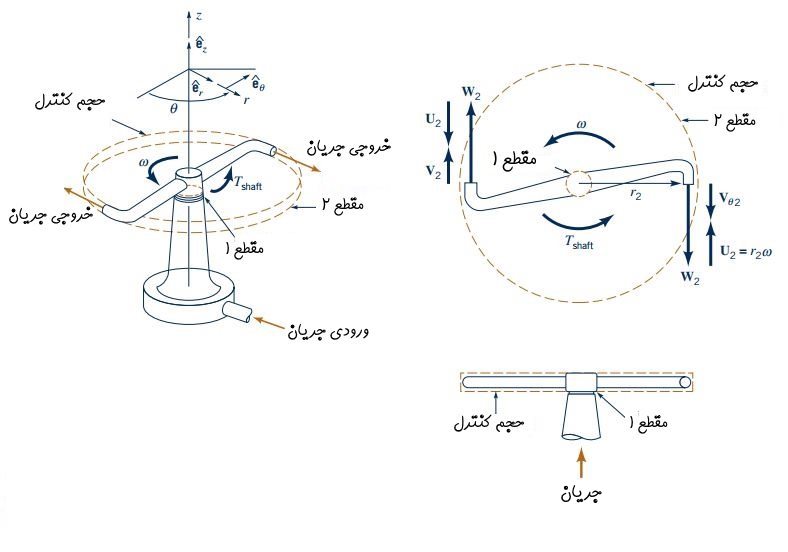
در این آب‌پاش، اندازه و جهت جریان سیال در ورودی (مقطع ۱) با خروجی (مقطع ۲) متفاوت است بنابراین جریان آب، یک گشتاور در قسمت بالای آب‌پاش ایجاد می‌کند و باعث چرخش این مجموعه در جهت نشان داده شده در شکل بالا، می‌شود. این موضوع مشابه فرآیندی است که به صورت رایج در پره‌های توربین مشاهده می‌شود.

برای اعمال رابطه مومنتوم زاویه‌ای (رابطه ۱۳) در این سیستم، حجم کنترل را به صورت ثابت و بدون تغییر شکل در نظر می‌گیریم. این حجم کنترل در شکل بالا به صورت خط‌چین و به کمک یک دیسک نشان داده شده است و شامل مرز‌هایی است که از یکسو قسمت خروجی آب از بخش فوقانی آب‌پاش و از سوی دیگر، بخش ورودی آب از پایین این دیسک را در بر می‌گیرد. این موضوع در شکل بالا به تصویر کشیده شده است.

همانند روشی که در محاسبه روابط مومنتوم خطی، پیوستگی و بقای جرم در قسمت‌های قبلی وبلاگ فرادرس بررسی شدند، رابطه‌ی سرعت‌های نسبی را در این مجموعه می‌توان به شکل زیر نمایش داد.

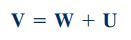
V سرعت سیالی را نشان می‌دهد که نسبت به سطح کنترل ثابت، محاسبه می‌شود. سرعت سیال در خروجی نازل که نسبت به خود نازل محاسبه می‌شود، با W نشان داده شده است. این سرعت را سرعت نسبی سیال می‌نامند. در این رابطه U سرعت نازل است که نسبت به سطح کنترل ثابت، اندازه‌گیری می‌شود.

عبارت دوم سمت چپ معادله مومنتوم زاویه‌ای (رابطه ۱۳)، مطابق شکل زیر است. عبارات ضرب خارجی و داخلی در این رابطه، جریان مومنتوم زاویه‌ای از مرز‌های سطح کنترل را نشان می‌دهند.

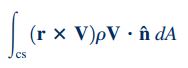
در این رابطه که بخشی از معادله مومنتوم زاویه‌ای است، زمانی که حاصل عبارت ضرب داخلی نشان داده شده ($$V.\hat{n}$$) مثبت باشد، جریان به سمت خارج از مرزهای حجم کنترل است و زمانی که جریان به سمت داخل مرزهای حجم کنترل باشد، عبارت $$V.\hat{n}$$ مقداری منفی دارد. شناسایی جهت مناسب در عبارت ضرب خارجی با استفاده از قانون دست راست، انجام می‌شود (برای دریافت اطلاعات بیشتر در زمینه ضرب خارجی به مطلب «ضرب خارجی بردارها — به زبان ساده» در وبلاگ فرادرس مراجعه کنید). در اینجا تمامی عبارات، حول محور دوران مشخصی، نوشته می‌شوند و در نهایت عبارت دوم سمت چپ معادله مومنتوم زاویه‌ای برای آب‌پاش نشان داده شده، به صورت زیر نوشته می‌شود.

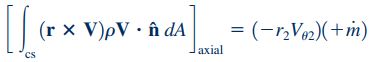
در این رابطه $$\dot{m}$$ برابر با نرخ جریان جرمی عبوری از هر دو نازل آب‌پاش است. نکته مهم دیگر در به کارگیری معادله مومنتوم زاویه‌ای، شیوه محاسبه ترم سمت راست معادله 13 است. این عبارت نمایانگر مجموع گشتاورهای خارجی‌ است که به سیستم وارد می‌شوند. همانطور که اشاره شد، برای محاسبه عبارت گشتاور در معادله مومنتوم زاویه‌ای در سیستم آب‌پاش، تنها گشتاورهایی را در نظر می‌گیریم که در راستای محور دوران بر سیستم اعمال می‌شوند. این عبارت به شکل زیر نمایش داده می‌شود.

در رابطه بالا فرض شده است که جهت T_shaft و چرخش آب‌پاش یکسان هستند. بنابراین رابطه مومنتوم زاویه‌ای برای آب‌پاشی که در شکل بالا نشان داده شده به فرم زیر است.

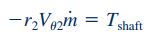
با توجه به رابطه‌ی بالا متوجه می‌شویم که T_shaft مقداری منفی دارد و بنابراین فرض یکسان بودن جهت T_shaft و چرخش آب‌پاش اشتباه است و گشتاور «شفت» (Shaft) عموما جهتی خلاف با جهت چرخش آب‌پاش دارد. این موضوع در حالت کلی در تجهیزات دوار مانند توربین‌ها صادق است.

نکته دیگری که در برخی از مسائل مورد استفاده قرار می‌گیرد، مفهوم «توان شفت» (Shaft Power) است. این مفهوم به صورت حاصل ضرب داخلی گشتاور شفت در سرعت دوران آن تعریف می‌شود و می‌توان آن را به فرم زیر نمایش داد.

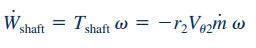
برای ساده‌سازی این رابطه در یک آب‌پاش توجه کنید که مقدار $$r_{2} \omega$$ برابر با سرعت هرکدام از نازل‌های خروجی آب‌پاش است که می‌توان آن را با U نشان داد. بنابراین رابطه توان شفت برای این آب‌پاش به صورت زیر قابل بازنویسی است.

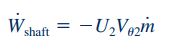
منفی بودن عبارت توان شفت در رابطه بالا نشان دهنده آن است که در این مثال، کار توسط سیال روی روتور و شفت انجام شده است.

اصولی که تا به اینجا برای محاسبه مومنتوم زاویه‌ای آب‌پاش توضیح داده شد را می‌توان در بسیاری از مسائل توربوماشین نیز مورد استفاده قرار داد. در حالت کلی، زمانی که معادله مومنتوم زاویه‌ای را در یک ماشین دوار بنویسیم که به صورت یک بعدی جریان دارد، در نهایت رابطه گشتاور و توان شفت به فرم زیر در می‌آید.

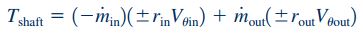
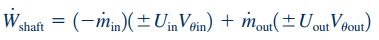
روابط بالا در حالت کلی نوشته شده‌اند و برای تعیین مقدار دقیق آن در هر مسئله نیاز به تعیین علامت‌های مثبت و منفی است که در این رابطه مشاهده می‌شوند. برای مثال علامت مثبت قبل از عبارت $$\dot{m}$$ زمانی استفاده می‌شود که جریان جرمی سیال مورد نظر به سمت خارج از حجم کنترل باشد و علامت منفی قبل از $$\dot{m}$$ برای حالتی است که جریان جرمی به سمت داخل حجم کنترل داشته باشیم. علامت مثبت و منفی دیگری نیز قبل از عبارت $$r v_{\theta}$$ وجود دارد و برای تعیین این علامت مثبت و منفی به شکل زیر عمل می‌شود:

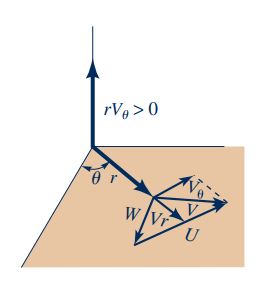
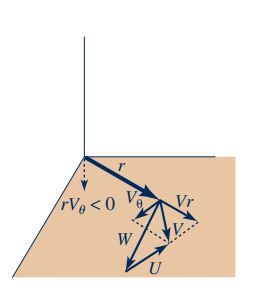
با توجه به شکل‌های بالا، زمانی که عبارت $$v_{\theta}$$ و U در یک جهت باشند، علامت $$r v_{\theta}$$ مثبت است و زمانی که عبارت $$v_{\theta}$$ و U خلاف جهت یکدیگر باشند علامت $$r v_{\theta}$$ منفی است. در ادامه در قالب مثالی، شیوه محاسبه اجزای مختلف رابطه مومنتوم زاویه‌ای را به طور دقیق مورد مطالعه قرار می‌دهیم.

مثال

آب‌پاشی را مطابق شکل زیر در نظر بگیرید. آب به قسمت چرخان این آب‌پاش از قسمت زیرین آن و با دبی حجمی 1000ml/s وارد می‌شود. قسمت خروجی این آب‌پاش از دو نازل تشکیل شده که سطح مقطع هرکدام از آن‌ها برابر با $$30mm^2$$ است و جریان سیال، مطابق شکل به صورت افقی و در جهت مماسی از این دو نازل خارج می‌شود. همچنین شعاع بین محور دوران و هرکدام از نازل‌ها برابر با 200mm است.

1. گشتاور لازم برای ثابت نگه داشتن قسمت بالای آب‌پاش را محاسبه کنید. دقت کنید که در این مثال سرعت خروج سیال از نازل برابر با 16.7m/s است.
2. گشتاور قسمت فوقانی آب‌پاش را در حالتی به دست آورید که در آن آب‌پاش با سرعت دورانی 500rev/min حول محور دوران در حال چرخش است.
3. سرعت آب‌پاش را در حالتی بیابید که هیچ گشتاوری به سیستم وارد نمی‌شود.

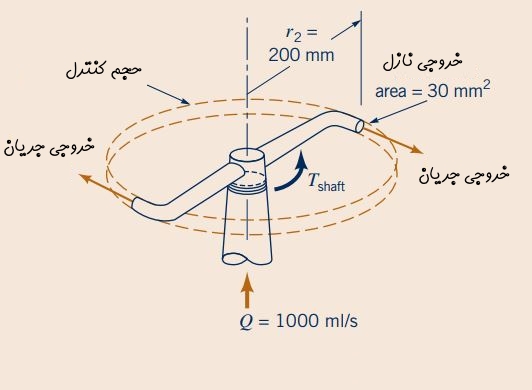
اولین گام در حل اکثر مسائل مکانیک سیالات تعیین مناسب حجم کنترل است. در این مثال و در هر سه بخش آن، حجم کنترل به صورت یک دیسک ساکن و بدون تغییر شکل در نظر گرفته می‌شود. این حجم کنترل در شکل بالا با خط‌چین نشان داده شده است. علاوه بر این، همانطور که در شکل بالا نیز مشاهده می‌شود، گشتاور محوری در این مسئله فقط گشتاوری است که در مقابل حرکت مقاومت می‌کند. این گشتاور با عبارت T_shaft در شکل به تصویر کشیده شده است.

در قسمت 1 این سوال، قسمت فوقانی آب‌پاش ساکن و رابطه بین سرعت‌ها در این قسمت را می‌توان مطابق شکل زیر نمایش داد.

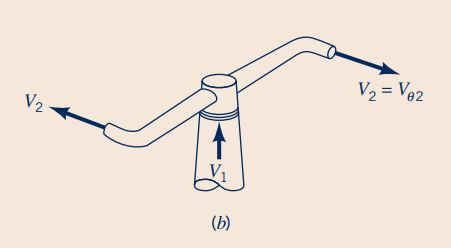
رابطه گشتاور شفت که در درسنامه برای آب‌پاش و در حالت کلی نوشته شده بود را می‌توان برای این مسئله خاص به صورت زیر نمایش داد.

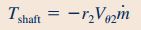
در این مثال همانطور که اشاره شد، حجم کنترل ساکن است و قابلیت تغییر شکل ندارد و سیال از هرکدام از نازل‌ها به صورت مماسی خارج می‌شود. بنابراین رابطه سرعت مماسی و گشتاور شفت را می‌توان به شکل زیر اصلاح کرد.

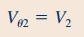
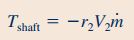
دبی جرمی در معادله بالا را می‌توان با استفاده از رابطه زیر محاسبه کرد.

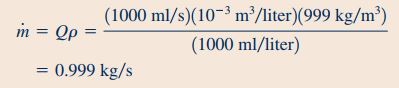
بنابراین با قرار دادن مقادیر شعاع، سرعت مماسی و دبی جرمی در رابطه گشتاور شفت، در نهایت گشتاور لازم برای ثابت نگه داشتن قسمت بالای آب‌پاش به شکل زیر محاسبه می‌شود.

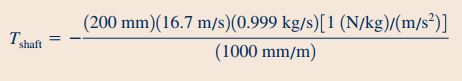
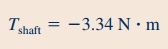
در قسمت ۲ این سوال و در حالتی که آب‌پاش با سرعت زاویه‌ای ثابت 500rpm می‌چرخد، جریان ذاتا ناپایا است ولی با توجه به اینکه سرعت زاویه‌ای ثابت و جهت خروج سیال همواره مماس بر دایره است، می‌توان جریان را به صورت پایا در نظر گرفت. بنابراین در اولین گام نیاز به تعیین رابطه بین سرعت‌ها داریم. در این قسمت، سرعت سیال در ورودی و خروجی حجم کنترل همانند شکل زیر در نظر گرفته می‌شود.

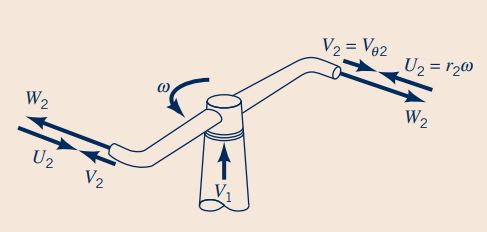
V₂، سرعت مطلق سیالی که از نازل خارج می‌شود را نشان می‌دهد و W₂ سرعت نسبی این سیال را بیان می‌کند و برابر با سرعت سیال خروجی از نازل در قسمت 1 است. اندازه این سرعت در صورت سوال برابر با 16.7m/s داده شده است. در ادامه رابطه بین سرعت‌های مختلف این قسمت از سوال به شکل زیر نوشته می‌شود.

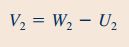
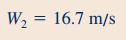
در معادله بالا U₂ سرعت نازل است که با استفاده از رابطه زیر محاسبه می‌شود.

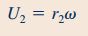
بنابراین با توجه به روابط بالا، سرعت مطلق سیال خروجی از نازل (V₂) قابل محاسبه است و برای به دست آوردن آن به شکل زیر عمل می‌کنیم.

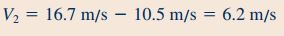
در نهایت با توجه به رابطه گشتاور و جریان جرمی که در قسمت ۱ سوال به دست آمدند، اندزه گشتاور شفت به صورت زیر محاسبه می‌شود.

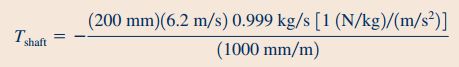
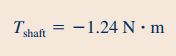
در قسمت ۳ سوال، هیچ گشتاوری به سیستم وارد نمی‌شود. در این حالت سرعت دورانی آب‌پاش تا مقدار ماکزیمم پیش می‌رود و در نهایت ثابت باقی می‌ماند. بنابراین رابطه گشتاور شفت که در دو قسمت قبلی سوال به دست آمد را می‌توان در این قسمت نیز به شکل زیر مورد استفاده قرار داد.

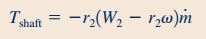
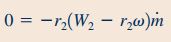
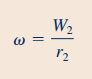
در نهایت باید پارامترهای سرعت و شعاع که اندازه آن‌ها معلوم هستند، در رابطه فوق جایگذاری شوند. در این حالت سرعت زاویه‌ای آب‌پاش برای سیستم بدون گشتاور، به شکل زیر محاسبه می‌شود.

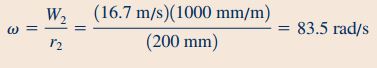
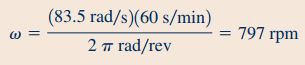
دقت کنید که در قسمت ۳ این سوال که گشتاور برابر با صفر است (0=T_shaft)، آب با مومنتوم زاویه‌ای صفر به حجم کنترل وارد و با همین مقدار مومنتوم زاویه‌ای از حجم کنترل خارج می‌شود.

در این مطلب مفهوم مومنتوم زاویه‌ای و روابط حاکم بر آن به صورت دقیق و کامل شرح داده شدند و نحوه استفاده از این روابط در قالب یک مثال مورد بررسی قرار گرفت. همانطور که اشاره شد بررسی مفاهیم پیوستگی، مومنتوم خطی، مومنتوم زاویه‌ای و قوانین بقا به عنوان پیش نیاز اساسی برای فهم معادلات ناویر استوکس معرفی می‌شوند. این موضوع را می‌توانید در مطلب معادلات ناویر استوکس به صورت دقیق مورد مطالعه قرار دهید.

در صورتی که به مباحث ارائه شده در این مطلب، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در علم مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• مجموعه آموزش‌های دروس مهندسی شیمی
• توربوماشین (Turbomachinery) — به زبان ساده
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
• دینامیک سیالات محاسباتی (CFD) — از صفر تا صد

^^