روش حجم محدود (Finite Volume Method) — از صفر تا صد

در مطالب قبلی وبلاگ فرادرس، بیان شد که برای انجام محاسبات عددی در علم دینامیک سیالات محاسباتی، روش‌های مختلفی مانند روش تفاضل محدود، روش حجم محدود و روش المان محدود وجود دارد.

همانطور که اشاره شد، برای توسعه و مطالعه روش تفاضل محدود از فرم دیفرانسیلی قوانین بقا مانند قانون بقای جرم (معادله پیوستگی) و قانون بقای مومنتوم (معادلات ناویر استوکس) استفاده می‌کنیم و با استفاده از تقریب تفاضل محدود، تقریبی برای محاسبه مشتقات جزئی به دست می‌آوریم.

این مطلب به صورت دقیق به بررسی یکی دیگر از روش‌های عددی برای انجام محاسبات در علم دینامیک سیالات محاسباتی می‌پردازد. این روش به نام روش حجم محدود معروف است که به صورت مستقیم با فرم انتگرالی معادلات بقا سر و کار دارد. بنابراین در ابتدا دانستن معادلات بقای مومنتوم خطی، پیوستگی و ناویر استوکس اهمیت بسیار زیادی دارد.

بعد از خواندن این مطلب شما به صورت دقیق تفاوت دو روش حجم محدود و تفاضل محدود را متوجه خواهید شد و قادر خواهید بود تا از روش حجم محدود برای انجام محاسبات عددی در مسائل مکانیک سیالات استفاده کنید.

روش حجم محدود در یک بعد

همانطور که اشاره شد، پیش نیاز و اساس روش حجم محدود، فرم انتگرالی معادلات بقا هستند. ایده اصلی این روش این است که ناحیه‌ای که محاسبات در آن انجام می‌شود را به چندین حجم محدود یا سلول تقسیم کنیم و انتگرال معادلات مربوط به قوانین بقا را در هرکدام از حجم کنترل‌ها تقریب بزنیم.

فیلم آموزش دینامیک سیالات محاسباتی CFD 1 در فرادرس

کلیک کنید

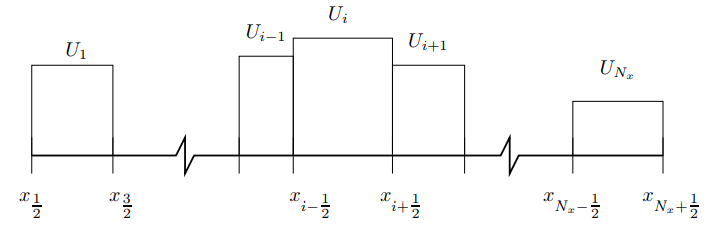
شکل زیر مثالی از شیوه تقسیم یک ناحیه محاسباتی در حالت یک بعدی به چندین سلول را به صورت دقیق ارائه کرده است. همانطور که مشاهده می‌شود، سلول شماره i بین دو نقطه $$x _ {i - {1 \over 2}}$$ و $$x _ {i + {1 \over 2}}$$ قرار گرفته است.

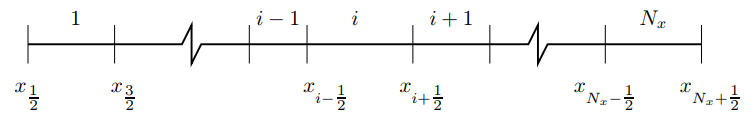
توجه شود که در حالت کلی ممکن است اندازه سلول‌ها با یکدیگر برابر نباشند و باید اشاره کرد که در شرایطی که سلول‌ها اندازه متفاوتی داشته باشند نیز معادلات موجود در روش حجم محدود قابل بیان هستند. برای مثال در دیواره‌ها و نقاطی که تغییرات در میدان زیاد است، شبکه حل باید ریز باشد و در نقاطی که تغییرات کمی در میدان جریان حضور دارد، مانند نقاط دور از دیواره، شبکه می‌تواند اندازه بزرگ‌تری را اختیار کند. انتخاب شبکه و بررسی اندازه آن در مطلب دینامیک سیالات محاسباتی به صورت دقیق مورد بررسی قرار گرفته است.

فرم انتگرالی معادله بقا را می‌توان در حالت کلی به شکل زیر بیان کرد.

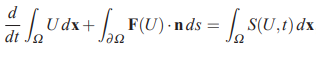
این معادله را می‌توان برای حالت یک بعدی به شکل زیر بازنویسی کرد.

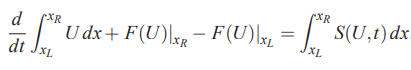
در ادامه ترم سمت راست معادله بالا را برابر با صفر (S=0) در نظر می‌گیریم. همچنین در صورتی که این معادله را به حجم کنترل i اعمال کنیم، رابطه زیر را داریم:

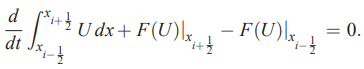
همانطور که مشاهده می‌شود برای محاسبه انتگرال از سطوح اطراف حجم کنترل استفاده شده که این سطوح در حالت یک بعدی با نمادهای $$x _ {i - {1 \over 2}}$$ و $$x _ {i + {1 \over 2}}$$ در شکل بالا نمایش داده شده‌اند.

در مرحله بعد ما می‌توانیم میانگین سرعت U در یک حجم کنترل i را با استفاده از رابطه زیر محاسبه کنیم.

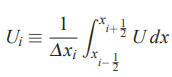
در این رابطه $$\Delta x _ i$$ با استفاده از رابطه زیر محاسبه می‌شود.

$$\Delta x _ i = x _ {i + {1 \over 2}} - x _ {i - {1 \over 2}} $$

در ادامه، رابطه 3 را می‌توان به شکل زیر بازنویسی کرد.

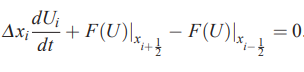
توجه کنید که تا به اینجای کار، هیچ تقریبی استفاده نشده و رابطه فوق یک رابطه دقیق به حساب می‌آید. در ادامه اولین فرض و تقریب را بر معادلات خود اعمال می‌کنیم. بر این اساس، می‌توانیم فرض کنیم که حل ما در هریک از حجم کنترل‌ها ثابت است. این موضوع را می‌توان با استفاده از رابطه زیر بیان کرد.

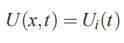
این رابطه و تقریب نشان می‌دهد که پاسخ حل در طول یک حجم کنترل مقدار ثابتی دارد و مقدار آن برابر با مقدار پاسخ در مرکز حجم کنترل قرار داده می‌شود. توجه کنید که رابطه و تقریب فوق، در محدوده بین $$x _ {i - {1 \over 2}}$$ و $$x _ {i + {1 \over 2}}$$ که مرزهای حجم کنترل را نشان می‌دهند، صادق است. این محدوده را می‌توان به شکل زیر بیان کرد.

$$x _ {i + {1 \over 2}} < x < x _ {i - {1 \over 2}} $$

بنابراین با توجه به توضیحاتی که در بالا داده شد، تقریب حجم محدود در حالت یک بعدی، به شکل زیر قابل نمایش است.

قدم بعدی در کنار فرضی که در بالا معرفی شد، این است که «فلاکس» (Flux) در مکان $$x _ {i - {1 \over 2}}$$ و $$x _ {i + {1 \over 2}}$$ در زمان t محاسبه شود.

نکته بسیار مهمی که باید در این قسمت توجه کنید این است که فرض حجم محدود در سطح مشترک بین دو سلول، نواحی را به صورت ناپیوسته تولید می‌کند. به عبارت دیگر، زمانی که به مکان $$x _ {i + {1 \over 2}}$$ از سمت چپ نزدیک می‌شویم، حل عددی ما برابر با مقدار در مکان i است که می‌توان رابطه آن را به شکل زیر نمایش داد.

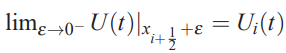
اما زمانی که از سمت راست به همین سلول نزدیک شویم، حل عددی ما برابر با مقدار موجود در سلول سمت راست، یعنی سلول i+1 می‌شود.

در ادامه و برای آنکه الگوریتم عددی ما موفق باشد، باید مطمئن شویم که فلاکس عددی استفاده شده، با خواص مسئله PDE سازگار است. در این قسمت به صورت خاص هدف ما این است که F را دقیقا برابر با فلاکس لحظه‌ای نظر بگیریم که این فلاکس لحظه‌ای با استفاده از قوانین بقا محاسبه شده است و شرایط اولیه آن در زمان t به تقریب عددی ما بستگی دارد.

بنابراین با توجه به توضیحات و روند بالا، روش حجم محدود را برای یک معادله جابه‌جایی یک بعدی مورد مطالعه قرار می‌دهیم. بر این اساس گام اول این است که یک معادله جابه‌جایی یک بعدی را به شکل زیر بنویسیم.

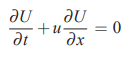
حل این معادله در زمان t با سرعت $$u (t)$$ جابه‌جا می‌شود. این موضوع را با استفاده از خطوط مشخصه و حل معادله مشخصه به راحتی می‌توان نمایش داد. بنابراین پاسخ این مسئله برای اولین لحظه بعد از زمان t که با استفاده از نماد $$t ^ + = t + \epsilon$$ نشان داده می‌شود، به شکل زیر خواهد بود.

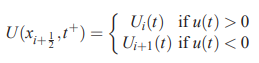
توجه کنید که $$ \epsilon$$ مقادیر بسیار کوچک را نمایش می‌دهد. در ادامه و با توجه به رابطه بالا می‌توان فلاکس را به صورت مستقیم با استفاده از مقادیر U به شکل زیر محاسبه کرد.

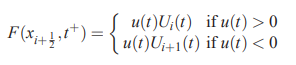
این رابطه را می‌توان به شکل زیر و بدون در نظر گرفتن علامت $$u (t)$$ نیز نمایش داد.

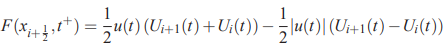
این فلاکس به آپویند یا «بادسو» (Upwind) معروف است. دلیل این نام گذاری این است که این فلاکس از مقدار بالادست U برای تعیین فلاکس استفاده می‌کند.

گام نهایی برای به دست آوردن تقریب گسسته کامل برای معادله یک بعدی جاله‌جایی این است که گسسته سازی معادله 5 را انجام دهیم. این کار با استفاده از یک روش انتگرالی در «معادلات دیفرانسیل معمولی» (Ordinary Differential Equation) امکان پذیر است. توجه کنید که معادلات دیفرانسیل معمولی را به صورت خلاصه با نماد ODE نیز نمایش می‌دهند. در این قسمت برای سادگی، از روش اویلر پیشرو استفاده می‌شود. بنابراین فرم نهایی و به صورت کامل گسسته شده روش حجم محدود به شکل زیر نوشته می‌شود.

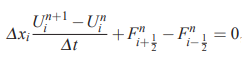
توجه کنید که این رابطه را به شکل زیر هم می‌توان نمایش داد.

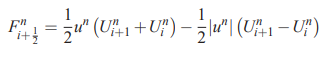
مثال 1

این مثال به بررسی دقیق اعمال روش حجم محدود در یک مسئله جابه‌جایی یک بعدی می‌پردازد.

کد متلبی که در ادامه آورده شده، معادله یک بعدی جابه‌جایی را با استفاده از روش حجم محدود مورد مطالعه قرار می‌دهد. این روش با استفاده از معادلات ۱۳ و ۱۴ در درسنامه فوق معرفی شده است.

نکته مهم دیگری که در این مثال و کد باید به آن دقت کنید این است که مسئله به صورت پریودیک در نظر گرفته شده و بنابراین هر آنچه که ناحیه محاسبات را در مکان $$ x = x _ R$$ ترک می‌کند باید در مکان $$ x = x _ L$$ به میدان حل وارد شود. کد متلب مربوط به این مثال در ادامه آورده شده است.

1 % This Matlab script solves the one-dimensional convection
2 % equation using a finite volume algorithm. The
3 % discretization forward Euler in time.
4
5 clear all;
6 close all;
7
8 % Number of points
9 Nx = 50;
10 x = linspace(0,1,Nx+1);
11 dx = 1/Nx;
12
13 % Calculate midpoint values of x in each control volume
14 xmid = 0.5*(x(1:Nx) + x(2:Nx+1));
15
16 % Set velocity
17 u = 1;
18
19 % Set final time
20 tfinal = 1;
21
22 % Set timestep
23 CFL = 0.5;
24 dt = CFL*dx/abs(u);
25
26 % Set initial condition to U0 = exp(-xˆ2)
27 % Note: technically, we should average the initial
28 % distribution in each cell but I chose to just set
29 % the value of U in each control volume to the midpoi
30 % value of U0.
31 U = 0.75*exp(-((xmid-0.5)/0.1).ˆ2)';
322 t = 0;
33
34 % Loop until t > tfinal
35 while (t < tfinal
36
37Ubc = [U(Nx); U; U(1)]; % This enforces the periodic bc
38
39 % Calculate the flux at each interface
40 F = 0.5* u *( Ubc(2:Nx+2) + Ubc(1:Nx+1)) ...
41 - 0.5*abs(u)*( Ubc(2:Nx+2) - Ubc(1:Nx+1));
42
43 % Calculate residual in each cell
44 R = F(2:Nx+1) - F(1:Nx);
45
46 % Forward Euler step
47 U = U - (dt/dx)*R;
48
49 % Increment time
50 t = t + dt;
51
52 % Plot current solution
53 stairs(x,[U; U(Nx)]);
54 axis([0, 1, -0.5, 1.5]);
55 grid on;
56 drawnow;
57
58 end
59
60 % overlay exact solution
61 U = 0.75*exp(-((xmid-0.5)/0.1).ˆ2)';
62 hold on;
63 stairs(x,[U; U(Nx)], 'r-');

روش حجم محدود در حالت دو بعدی

در بخش قبل به بررسی روش حجم محدود و گسسته سازی معادلات موجود در دینامیک سیالات محاسباتی در حالت یک بعدی پرداخته شد.

فیلم آموزش شبیه سازی مسائل جریان سیال و انتقال حرارت با فرترن Fortran در فرادرس

کلیک کنید

گسسته سازی حجم محدود را می‌توانیم به مسائلی با ابعاد بالاتر نیز تعمیم دهیم. بنابراین در ادامه فرض کنید که ناحیه حل فیزیکی ما به چندین حجم کنترل مثلثی تقسیم شده باشد. این موضوع در شکل زیر به خوبی نشان داده شده است.

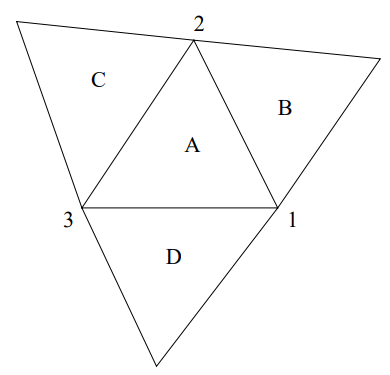
برای حجم کنترل نشان داده شده، رابطه ۱ را می‌توان به شکل زیر بیان کرد.

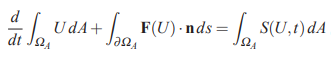
در این رابطه، $$\Omega _ A$$ نشان دهنده فضای داخلی حجم کنترل A است و $$\partial \Omega _ A$$ مرز حجم کنترل A را نشان می‌دهد. در ادامه و مشابه با حالت یک بعدی، میانگین سلول با استفاده از رابطه زیر قابل محاسبه است.

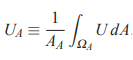
در رابطه بالا، A مساحت حجم کنترل را نشان می‌دهد. بنابراین می‌توان رابطه 15 را به شکل زیر بازنویسی کرد.

در مسئله جابه‌جایی می‌توان مشابه بخش‌های قبل مقدار S را برابر با صفر (S=0) در نظر گرفت. علاوه بر این موضوع، باید انتگرال سطح موجود در رابطه بالا را به سه سطح مثلث (حجم کنترل انتخاب شده به شکل مثلث در نظر گرفته شده است) تقسیم کنیم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

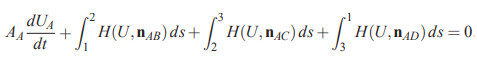
در معادله بالا، رابطه $$H(U,n)=F(U).n$$ برقرار است. نکته مهم دیگری که باید به آن اشاره کرد این است که پارامتر $$n _ {AB}$$ بردار نرمال بین سلول A و B را نشان می‌دهد. این موضوع و مفهوم را می‌توان برای پارامترهای $$n _ {AC}$$ و $$n _ {AD}$$ نیز تعمیم داد و این دو پارامتر را به همین صورت تعریف کرد.

در ادامه و مشابه با حالت یک بعدی، فرض می‌شود که پاسخ مورد نظر ما در تمام نقاط حجم کنترل برابر با مقدار میانگین در سلول است. نکته مهم دیگر این است که فلاکس در هر سطح مشترک را می‌توان با روش بادسو یا «آپویند» (Upwind) محاسبه کرد. برای مثال برای سطح مشترک بین دو سلول A و B رابطه زیر قابل بیان است.

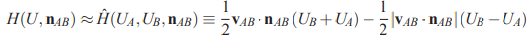
عبارت $$v _ {AB}$$ سرعت بین حجم‌های کنترل را نشان می‌دهد. بنابراین زمانی که $$v _ {AB}.n _ {AB}>0$$ باشد، فلاکس با توجه به حالت سلول A اندازه‌گیری شده و به عبارت دیگر برابر با $$U _ {A}$$ است و در سمت مقابل اگر $$v _ {AB}.n _ {AB}<0$$ باشد، فلاکس با توجه به حالت سلول B اندازه‌گیری شده و به عبارت دیگر برابر با $$U _ {B}$$ است.

توجه کنید که سرعت $$v _ {AB}$$ معمولا تقریب مناسبی از سرعت در نقطه میانی خط بین دو سطح A و B است. نکته مهم دیگری که باید به آن اشاره کرد این است که در حالت دو بعدی v تابعی از x است و برای حالت جریان غیرقابل تراکم نیز رابطه زیر بین سرعت‌ها برقرار است.

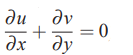
نکته دیگری که باید به آن توجه کرد این است که علامت $$\hat {H}$$ نشان می‌دهد که وقتی v ثابت نیست، فلاکس محاسبه شده، یک تقریب از فلاکس واقعی را بیان می‌کند. بنابراین با توجه به توضیحات بالا رابطه 18 را می‌توان به شکل زیر بازنویسی کرد.

در نهایت قدم نهایی این است که انتگرال گیری روی زمان انجام شود. همانطور که در قسمت قبل نشان داده شد، برای انتگرال گیری روی زمان می‌توان از الگوریتم پیشرو اویلر استفاده کرد و در نهایت حالت نهایی گسسته شده روش حجم محدود به شکل زیر قابل بیان است.

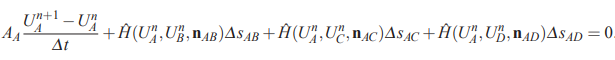
مثال 2

در این مثال از روش حجم محدود برای حل مسئله دو بعدی جابه‌جایی در یک مش مستطیلی استفاده می شود. برای این منظور از یک کد متلب که معادلات دو بعدی جابه‌جایی را با استفاده از روش حجم محدود دو بعدی حل می‌کند استفاده شده است.

همانطور که اشاره شد، مش این حل به صورت مستطیلی فرض شده است. بنابراین رابطه 22 که برای سلول مثلثی نوشته شده را باید برای سلول‌های مستطیلی بازنویسی کرد. نکته دیگری که باید به آن اشاره کرد این است که در این مسئله، شرط مرزی به صورت پریودیک فرض شده و سرعت مقداری ثابت دارد. کد متلب این مسئله در ادامه آورده شده است.

1% This Matlab script solves the one-dimensional convection
2 % equation using a finite volume algorithm. The
3 % discretization forward Euler in time.
4
5 clear all;
6 close all;
7
8 % Number of points
9 Nx = 50;
10 x = linspace(0,1,Nx+1);
11 dx = 1/Nx;
12
13 % Calculate midpoint values of x in each control volume
14 xmid = 0.5*(x(1:Nx) + x(2:Nx+1));
15
16 % Set velocity
17 u = 1;
18
19 % Set final time
20 tfinal = 1;
21
22 % Set timestep
23 CFL = 0.5;
24 dt = CFL*dx/abs(u);
25
26 % Set initial condition to U0 = exp(-xˆ2)
27 % Note: technically, we should average the initial
28 % distribution in each cell but I chose to just set
29 % the value of U in each control volume to the midpoint
30 % value of U0.
31 U = 0.75*exp(-((xmid-0.5)/0.1).ˆ2)';
32 t = 0;
33
34 % Loop until t > tfinal
35 while (t < tfinal),
36
37 Ubc = [U(Nx); U; U(1)]; % This enforces the periodic bc
38
39 % Calculate the flux at each interface
40 F = 0.5* u *( Ubc(2:Nx+2) + Ubc(1:Nx+1)) ...
41 - 0.5*abs(u)*( Ubc(2:Nx+2) - Ubc(1:Nx+1));
42
43 % Calculate residual in each cell
44 R = F(2:Nx+1) - F(1:Nx);
45
46 % Forward Euler step
47 U = U - (dt/dx)*R;
48
49 % Increment time
50 t = t + dt;
51
52 % Plot current solution
53 stairs(x,[U; U(Nx)]);
54 axis([0, 1, -0.5, 1.5]);
55 grid on;
56 drawnow;
57
58 end
59
60 % overlay exact solution
61 U = 0.75*exp(-((xmid-0.5)/0.1).ˆ2)';
62 hold on;
63 stairs(x,[U; U(Nx)], 'r-');

روش حجم محدود برای سیستم‌های غیر خطی

روش حجم محدود پایه که در بالا معرفی شد را می‌توان برای سیستم معادلات غیر خطی نیز تعمیم داد. این سیستم معادلات اویلر را شامل شود. مسئله اصلی در این شرایط، محاسبه فلاکس است.

فیلم آموزش شبیه سازی مسائل جریان سیال و انتقال حرارت با فرترن Fortran در فرادرس

کلیک کنید

در حالت یک بعدی، گسسته سازی در روش حجم محدود پایه، تغییری نمی‌کند و به شکل معادله ۱۴ باقی می‌ماند. این معادله را می‌توان به شکل زیر بیان کرد.

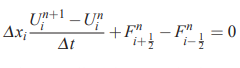
در ادامه می‌توان با استفاده از رابطه معروف فلاکس «لکس فردریش» (Lax-Friedrichs) روابط بالا را بازنویسی کرد. بنابراین داریم:

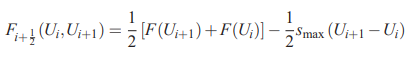
در این رابطه S_max ماکزیمم سرعت انتشار اغتشاشات کوچک را برای حالات $$U _ i$$ و $$U _ {i+1}$$ نشان می‌دهد.

این مطلب به صورت دقیق به مطالعه روش حجم محدود پرداخته است. بدین منظور ابتدا روش یک بعدی حجم محدود به همراه مثال مورد بررسی قرار گرفت و در ادامه به مطالعه روش حجم محدود در حالت دو بعدی پرداخته شد و در انتهای مطلب نیز روش حجم محدود برای سیستم‌های غیر خطی مورد مطالعه قرار گرفت.

همانطور که بیان شد روش حجم محدود در کنار روش‌های المان محدود و تفاضل محدود از جمله روش‌های عددی پرکاربرد برای حل معادلات ناویر استوکس و پیوستگی هستند و کاربرد زیادی در علم دینامیک سیالات محاسباتی دارند. همچنین پایداری این روش‌های عددی نیز یکی از موارد بسیار مهم در علم مکانیک سیالات محسوب می‌شود. به عنوان مثال بررسی پایداری روش تفاضل محدود در وبلاگ فرادرس به صورت دقیق مورد بررسی قرار گرفته است.

در صورتی که به مباحث ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در علم مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
• ویسکوزیته (Viscosity) — به زبان ساده
• پایداری روش تفاضل محدود — به زبان ساده
• روش تفاضل محدود (Finite Difference Method) — از صفر تا صد

^^