بهینه سازی (ریاضیاتی) چیست؟ — راهنمای جامع

«بهینه سازی ریاضیاتی» (Mathematical Optimization) که به آن «برنامهنویسی ریاضیاتی» (Mathematical Programming) نیز گفته میشود، فرایندی است که در آن بهترین جواب (با توجه به مجموعهای از معیارها) از میان مجموعهای از جوابهای ممکن، برای یک مسأله خاص انتخاب میشود. امروزه مسائل بهینه سازی در تمامی رشتههای علمی کَمی (Quantitative Disciplines) نظیر «علوم کامپیوتر» (Computer Science)، مهندسی (Engineering)، «تحقیق در عملیات» (Operations Research)، «اقتصاد» (Economics) و سایر موارد مورد استفاده قرار میگیرند. در طول قرنهای متمادی، توسعه روشهای تولید جواب و حل مسأله، یکی از حوزههای مهم تحقیقاتی در علم «ریاضیات» (Mathematics) بوده است و اهمیت آنها در طی چند سال گذشته چند برابر شده است.
جهت درک بهتر و اصولیتر حوزه بهینه سازی (ریاضیاتی)، ابتدا لازم است تا شناخت کافی در مورد مسائل بهینه سازی ایجاد شود. به بیان ساده، در یک «مسأله بهینه سازی» (Optimization Problems)، هدف «کمینهسازی» (Minimizing) یا «بیشینهسازی» (Maximizing) یک «تابع حقیقی» (Real Function) است؛ برای چنین کاری سیستم بهینه سازی ریاضیاتی، به طور سیستماتیک، مقادیر ورودی را از یک مجموعه مجاز از مقادیر انتخاب و پس از آن، مقدار تابع حقیقی را محاسبه میکند.
تعمیم نظریه بهینه سازی (Optimization Theory) و تکنیکهای آن به دیگر حوزههای علمی و تحقیقاتی مرتبط، در حیطه کاربردهای مهم رشته «ریاضیات کاربردی» (Applied Mathematics) محسوب میشود. به طور کلی، اصطلاح بهینه سازی به فرایندی اطلاق میشود که هدف آن پیدا کردن بهترین مقادیر یک (یا چند) «تابع هدف» (Objective Functions) در یک دامنه تعریف شده است.

مؤلفههای یک مدل بهینه سازی
بهینه سازی ابزار مهمی در «تصمیمگیری» (Decision Making) و تحلیل سیستمهای فیزیکی محسوب میشود.
از نظر ریاضی، یک مسأله بهینه سازی، مسأله پیدا کردن بهترین جواب از میان مجموعهای از جوابهای کاندید (Candidate) یا امکانپذیر (Feasible) است.

ساختن یک مدل بهینه سازی
اولین گام در فرایند بهینه سازی، ساختن یک مدل مناسب برای بهینه سازی است؛ مدلسازی (Modelling)، به فرایند شناسایی و نمایش ریاضی «هدف» (Objective)، «متغیرها» (Variables) و «قیدهای» (Constraints) مسأله گفته میشود:
- هدف (Objective)، معیار کمی عملکرد سیستم است که قرار است کمینه یا بیشینه شود. به عنوان نمونه، در «تولید» (Manufacturing) هدف کمینهسازی هزینههای تولید و یا بیشینهسازی سود است. در حالی که در برازش دادهها (Data Fitting) روی یک مدل، هدف کمینهسازی انحراف کل دادههای مشاهده شده (Observed Data) از دادههای پیشبینی شده (Predicted Data) است.
- متغیرها (Variables) یا به عبارت دیگر «ناشناختهها» (Unknowns)، مؤلفههایی از مدل بهینه سازی محسوب میشوند که قرار است مقادیر مناسبی برای آنها یافت شود. به عنوان نمونه در فرایند تولید، متغیرها میتوانند پارامترهایی نظیر مقدار منابع مصرف شده و یا زمان صرف شده در هر فعالیت باشد. در حالی که در برازش دادهها، متغیرها همان پارامترهای مدل خواهند بود.
- قیدها (Constraints) توابعی هستند که روابط میان متغیرها (Variables) را نشان میدهد و از این طریق، مقادیر مجاز برای متغیرها مشخص میشود. به عنوان نمونه در فرایند تولید، مقدار منابع مصرف شده نمیتواند از مقدار منابع در دسترس فراتر برود.
مشخص کردن نوع مسأله بهینه سازی
گام دوم در فرایند بهینه سازی، مشخص کردن نوع و یا طبقهبندی مسألهای است که قرار است بهینهسازی شود. در ادامه و در بخشهای بعدی، طبقهبندی مسائل بهینه سازی ارائه خواهد شد. پس از این مرحله و مشخص شدن نوع مسأله بهینهسازی، نیاز است تا بسته به دامنه و نیازهای مسأله، از میان ابزارهای بهینهسازی موجود (تجاری و آکادمیک) برای بهینهسازی توابع و پیدا کردن جوابهای بهینه (یا تقریبی از آنها)، ابزاری که بیشترین تطابق را با نیازهای مسأله دارد، انتخاب کرد و آن را در دامنه مورد نظر مورد استفاده قرار داد.
مسائل بهینه سازی (Optimization Problems)
مسائل بهینه سازی را میتوان به شکل زیر نمایش داد:
با داشتن: یک تابع به فرم $$f : A \rightarrow R$$ که مقادیر را از مجموعهای نظیر $$A$$ (دامنه مسأله) به اعداد حقیقی (Real Numbers) نگاشت میکند.
هدف: پیدا کردن عنصری مثل $$X _ { 0 } \in A$$ است، به طوری که شرط $$f ( X _ { 0 }) \leq f ( X) \;\;\; f o r \; a l l\;\;\ \; X \in A$$ (برای مسائل کمینهسازی) یا شرط $$f ( X _ { 0 }) \geq f ( X) \;\;\; f o r \; a l l\;\;\ \; X \in A$$ (برای مسائل بیشینهسازی) برقرار باشد.
به فرمولبندی مسائل به شکل نشان داده شده، نمایش مسأله بهینه سازی یا نمایش مسأله برنامهنویسی ریاضی (Mathematical Programming Problem) گفته میشود. نکته بسیار مهم در مورد مسائل بهینهسازی این است که بسیاری از مسائل «جهان واقعی» (Real-World) و مسائل تئوری را میتوان از طریق چارچوب عمومی نمایش داده شده مدلسازی کرد. به فرمول بندی مسائل بهینه سازی در قالب زیر توجه کنید:
$$f ( X _ { 0 } ) \geq f ( X ) \;\;\; \Leftrightarrow \;\;\; \widetilde { f } ( X _ { 0 } ) \leq \widetilde { f } ( X )$$
$$\widetilde { f } ( X ) :=- f ( X ) , \;\;\;\;\; \widetilde { f }:A \rightarrow R$$
با توجه به این که فرمولبندی مسائل بهینه سازی در قالب مسائل کمینهسازی (فرمولبندی بالا)، معتبر (Valid) است، در چنین حالتی حل کردن مسائل کمینه سازی (با استفاده از فرمولبندی نمایش داده شده) سادهتر خواهد بود. با این حال، فرمولبندی مسائل بهینه سازی در قالب مسائل بیشینهسازی نیز معتبر خواهد بود.
مفاهیم اولیه در بهینه سازی (ریاضیاتی)
روشهای بهینه سازی، یکی از معتبرترین و قابل قبولترین روشهای حل مسأله در حوزههای مختلف علمی محسوب میشوند. به عنوان نمونه، در رشته فیزیک، به مسائلی که از طریق چارچوب بالا فرمولبندی شوند، تکنیکهای «کمینهسازی انرژی» (Energy Minimization) گفته میشود.
به عبارت دیگر در اصل، مقدار تابع $$f$$ انرژی سیستمی که مدلسازی شده است را نشان میدهد. از جمله سیستمهای بهینه سازی که از مفاهیم موجود در حوزه فیزیک («فیزیک آماری» (Statistical Physics)) استفاده میکنند، میتواند به الگوریتم «بهینه سازی اکسترمال» (Extremal Optimization) اشاره کرد. در ادامه، کدهای پیادهسازی الگوریتم بهینه سازی اکسترمال در زبان Ruby نمایش داده شده است:
1def euc_2d(c1, c2)
2 Math.sqrt((c1[0] - c2[0])**2.0 + (c1[1] - c2[1])**2.0).round
3end
4
5def cost(permutation, cities)
6 distance =0
7 permutation.each_with_index do |c1, i|
8 c2 = (i==permutation.size-1) ? permutation[0] : permutation[i+1]
9 distance += euc_2d(cities[c1], cities[c2])
10 end
11 return distance
12end
13
14def random_permutation(cities)
15 perm = Array.new(cities.size){|i| i}
16 perm.each_index do |i|
17 r = rand(perm.size-i) + i
18 perm[r], perm[i] = perm[i], perm[r]
19 end
20 return perm
21end
22
23def calculate_neighbor_rank(city_number, cities, ignore=[])
24 neighbors = []
25 cities.each_with_index do |city, i|
26 next if i==city_number or ignore.include?(i)
27 neighbor = {:number=>i}
28 neighbor[:distance] = euc_2d(cities[city_number], city)
29 neighbors << neighbor
30 end
31 return neighbors.sort!{|x,y| x[:distance] <=> y[:distance]}
32end
33
34def get_edges_for_city(city_number, permutation)
35 c1, c2 = nil, nil
36 permutation.each_with_index do |c, i|
37 if c == city_number
38 c1 = (i==0) ? permutation.last : permutation[i-1]
39 c2 = (i==permutation.size-1) ? permutation.first : permutation[i+1]
40 break
41 end
42 end
43 return [c1, c2]
44end
45
46def calculate_city_fitness(permutation, city_number, cities)
47 c1, c2 = get_edges_for_city(city_number, permutation)
48 neighbors = calculate_neighbor_rank(city_number, cities)
49 n1, n2 = -1, -1
50 neighbors.each_with_index do |neighbor,i|
51 n1 = i+1 if neighbor[:number] == c1
52 n2 = i+1 if neighbor[:number] == c2
53 break if n1!=-1 and n2!=-1
54 end
55 return 3.0 / (n1.to_f + n2.to_f)
56end
57
58def calculate_city_fitnesses(cities, permutation)
59 city_fitnesses = []
60 cities.each_with_index do |city, i|
61 city_fitness = {:number=>i}
62 city_fitness[:fitness] = calculate_city_fitness(permutation, i, cities)
63 city_fitnesses << city_fitness
64 end
65 return city_fitnesses.sort!{|x,y| y[:fitness] <=> x[:fitness]}
66end
67
68def calculate_component_probabilities(ordered_components, tau)
69 sum = 0.0
70 ordered_components.each_with_index do |component, i|
71 component[:prob] = (i+1.0)**(-tau)
72 sum += component[:prob]
73 end
74 return sum
75end
76
77def make_selection(components, sum_probability)
78 selection = rand()
79 components.each_with_index do |component, i|
80 selection -= (component[:prob] / sum_probability)
81 return component[:number] if selection <= 0.0
82 end
83 return components.last[:number]
84end
85
86def probabilistic_selection(ordered_components, tau, exclude=[])
87 sum = calculate_component_probabilities(ordered_components, tau)
88 selected_city = nil
89 begin
90 selected_city = make_selection(ordered_components, sum)
91 end while exclude.include?(selected_city)
92 return selected_city
93end
94
95def vary_permutation(permutation, selected, new, long_edge)
96 perm = Array.new(permutation)
97 c1, c2 = perm.rindex(selected), perm.rindex(new)
98 p1,p2 = (c1<c2) ? [c1,c2] : [c2,c1]
99 right = (c1==perm.size-1) ? 0 : c1+1
100 if perm[right] == long_edge
101 perm[p1+1..p2] = perm[p1+1..p2].reverse
102 else
103 perm[p1...p2] = perm[p1...p2].reverse
104 end
105 return perm
106end
107
108def get_long_edge(edges, neighbor_distances)
109 n1 = neighbor_distances.find {|x| x[:number]==edges[0]}
110 n2 = neighbor_distances.find {|x| x[:number]==edges[1]}
111 return (n1[:distance] > n2[:distance]) ? n1[:number] : n2[:number]
112end
113
114def create_new_perm(cities, tau, perm)
115 city_fitnesses = calculate_city_fitnesses(cities, perm)
116 selected_city = probabilistic_selection(city_fitnesses.reverse, tau)
117 edges = get_edges_for_city(selected_city, perm)
118 neighbors = calculate_neighbor_rank(selected_city, cities)
119 new_neighbor = probabilistic_selection(neighbors, tau, edges)
120 long_edge = get_long_edge(edges, neighbors)
121 return vary_permutation(perm, selected_city, new_neighbor, long_edge)
122end
123
124def search(cities, max_iterations, tau)
125 current = {:vector=>random_permutation(cities)}
126 current[:cost] = cost(current[:vector], cities)
127 best = current
128 max_iterations.times do |iter|
129 candidate = {}
130 candidate[:vector] = create_new_perm(cities, tau, current[:vector])
131 candidate[:cost] = cost(candidate[:vector], cities)
132 current = candidate
133 best = candidate if candidate[:cost] < best[:cost]
134 puts " > iter #{(iter+1)}, curr=#{current[:cost]}, best=#{best[:cost]}"
135 end
136 return best
137end
138
139if __FILE__ == $0
140 # problem configuration
141 berlin52 = [[565,575],[25,185],[345,750],[945,685],[845,655],
142 [880,660],[25,230],[525,1000],[580,1175],[650,1130],[1605,620],
143 [1220,580],[1465,200],[1530,5],[845,680],[725,370],[145,665],
144 [415,635],[510,875],[560,365],[300,465],[520,585],[480,415],
145 [835,625],[975,580],[1215,245],[1320,315],[1250,400],[660,180],
146 [410,250],[420,555],[575,665],[1150,1160],[700,580],[685,595],
147 [685,610],[770,610],[795,645],[720,635],[760,650],[475,960],
148 [95,260],[875,920],[700,500],[555,815],[830,485],[1170,65],
149 [830,610],[605,625],[595,360],[1340,725],[1740,245]]
150 # algorithm configuration
151 max_iterations = 250
152 tau = 1.8
153 # execute the algorithm
154 best = search(berlin52, max_iterations, tau)
155 puts "Done. Best Solution: c=#{best[:cost]}, v=#{best[:vector].inspect}"
156endهمچنین در حوزه «هوش مصنوعی» (Artificial Intelligence) و «یادگیری ماشین» (Machine Learning) نیز بسیار حیاتی است که کیفیت «مدل داده» (Data Model)، به طور پیوسته و توسط یک «تابع هزینه» (Cost Function) ارزیابی شود؛ در این حالت، منظور از کمینهسازی تابع هزینه، پیدا کردن مجموعهای از «پارامترهای بهینه» (Optimal Parameters) است که سبب تولید مقدار بهینه خطا (کمترین خطای ممکن) در سیستم میشوند.
از جمله الگوریتمهای بهینه سازی که در دسته «الگوریتمهای تخمین توزیع» (Estimation of Distribution Algorithms) قرار میگیرد، میتوان به الگوریتم «بهینه سازی بیزی» (Bayesian Optimization) اشاره کرد. در ادامه، کدهای پیادهسازی الگوریتم بهینه سازی بیزی در زبان Ruby نمایش داده شده است:
1def onemax(vector)
2 return vector.inject(0){|sum, value| sum + value}
3end
4
5def random_bitstring(size)
6 return Array.new(size){ ((rand()<0.5) ? 1 : 0) }
7end
8
9def path_exists?(i, j, graph)
10 visited, stack = [], [i]
11 while !stack.empty?
12 return true if stack.include?(j)
13 k = stack.shift
14 next if visited.include?(k)
15 visited << k
16 graph[k][:out].each {|m| stack.unshift(m) if !visited.include?(m)}
17 end
18 return false
19end
20
21def can_add_edge?(i, j, graph)
22 return !graph[i][:out].include?(j) && !path_exists?(j, i, graph)
23end
24
25def get_viable_parents(node, graph)
26 viable = []
27 graph.size.times do |i|
28 if node!=i and can_add_edge?(node, i, graph)
29 viable << i
30 end
31 end
32 return viable
33end
34
35def compute_count_for_edges(pop, indexes)
36 counts = Array.new(2**(indexes.size)){0}
37 pop.each do |p|
38 index = 0
39 indexes.reverse.each_with_index do |v,i|
40 index += ((p[:bitstring][v] == 1) ? 1 : 0) * (2**i)
41 end
42 counts[index] += 1
43 end
44 return counts
45end
46
47def fact(v)
48 return v <= 1 ? 1 : v*fact(v-1)
49end
50
51def k2equation(node, candidates, pop)
52 counts = compute_count_for_edges(pop, [node]+candidates)
53 total = nil
54 (counts.size/2).times do |i|
55 a1, a2 = counts[i*2], counts[(i*2)+1]
56 rs = (1.0/fact((a1+a2)+1).to_f) * fact(a1).to_f * fact(a2).to_f
57 total = (total.nil? ? rs : total*rs)
58 end
59 return total
60end
61
62def compute_gains(node, graph, pop, max=2)
63 viable = get_viable_parents(node[:num], graph)
64 gains = Array.new(graph.size) {-1.0}
65 gains.each_index do |i|
66 if graph[i][:in].size < max and viable.include?(i)
67 gains[i] = k2equation(node[:num], node[:in]+[i], pop)
68 end
69 end
70 return gains
71end
72
73def construct_network(pop, prob_size, max_edges=3*pop.size)
74 graph = Array.new(prob_size) {|i| {:out=>[], :in=>[], :num=>i} }
75 gains = Array.new(prob_size)
76 max_edges.times do
77 max, from, to = -1, nil, nil
78 graph.each_with_index do |node, i|
79 gains[i] = compute_gains(node, graph, pop)
80 gains[i].each_with_index {|v,j| from,to,max = i,j,v if v>max}
81 end
82 break if max <= 0.0
83 graph[from][:out] << to
84 graph[to][:in] << from
85 end
86 return graph
87end
88
89def topological_ordering(graph)
90 graph.each {|n| n[:count] = n[:in].size}
91 ordered,stack = [], graph.select {|n| n[:count]==0}
92 while ordered.size < graph.size
93 current = stack.shift
94 current[:out].each do |edge|
95 node = graph.find {|n| n[:num]==edge}
96 node[:count] -= 1
97 stack << node if node[:count] <= 0
98 end
99 ordered << current
100 end
101 return ordered
102end
103
104def marginal_probability(i, pop)
105 return pop.inject(0.0){|s,x| s + x[:bitstring][i]} / pop.size.to_f
106end
107
108def calculate_probability(node, bitstring, graph, pop)
109 return marginal_probability(node[:num], pop) if node[:in].empty?
110 counts = compute_count_for_edges(pop, [node[:num]]+node[:in])
111 index = 0
112 node[:in].reverse.each_with_index do |v,i|
113 index += ((bitstring[v] == 1) ? 1 : 0) * (2**i)
114 end
115 i1 = index + (1*2**(node[:in].size))
116 i2 = index + (0*2**(node[:in].size))
117 a1, a2 = counts[i1].to_f, counts[i2].to_f
118 return a1/(a1+a2)
119end
120
121def probabilistic_logic_sample(graph, pop)
122 bitstring = Array.new(graph.size)
123 graph.each do |node|
124 prob = calculate_probability(node, bitstring, graph, pop)
125 bitstring[node[:num]] = ((rand() < prob) ? 1 : 0)
126 end
127 return {:bitstring=>bitstring}
128end
129
130def sample_from_network(pop, graph, num_samples)
131 ordered = topological_ordering(graph)
132 samples = Array.new(num_samples) do
133 probabilistic_logic_sample(ordered, pop)
134 end
135 return samples
136end
137
138def search(num_bits, max_iter, pop_size, select_size, num_children)
139 pop = Array.new(pop_size) { {:bitstring=>random_bitstring(num_bits)} }
140 pop.each{|c| c[:cost] = onemax(c[:bitstring])}
141 best = pop.sort!{|x,y| y[:cost] <=> x[:cost]}.first
142 max_iter.times do |it|
143 selected = pop.first(select_size)
144 network = construct_network(selected, num_bits)
145 arcs = network.inject(0){|s,x| s+x[:out].size}
146 children = sample_from_network(selected, network, num_children)
147 children.each{|c| c[:cost] = onemax(c[:bitstring])}
148 children.each {|c| puts " >>sample, f=#{c[:cost]} #{c[:bitstring]}"}
149 pop = pop[0...(pop_size-select_size)] + children
150 pop.sort! {|x,y| y[:cost] <=> x[:cost]}
151 best = pop.first if pop.first[:cost] >= best[:cost]
152 puts " >it=#{it}, arcs=#{arcs}, f=#{best[:cost]}, [#{best[:bitstring]}]"
153 converged = pop.select {|x| x[:bitstring]!=pop.first[:bitstring]}.empty?
154 break if converged or best[:cost]==num_bits
155 end
156 return best
157end
158
159if __FILE__ == $0
160 # problem configuration
161 num_bits = 20
162 # algorithm configuration
163 max_iter = 100
164 pop_size = 50
165 select_size = 15
166 num_children = 25
167 # execute the algorithm
168 best = search(num_bits, max_iter, pop_size, select_size, num_children)
169 puts "done! Solution: f=#{best[:cost]}/#{num_bits}, s=#{best[:bitstring]}"
170endدر فرمولبندی مسائل بهینه سازی (Optimization Problems)، مجموعه $$A$$ زیر مجموعهای از «فضای اقلیدسی» (Euclidean Space) یا $$R ^ { n }$$ است. معمولا در مسائل بهینه سازی، برای $$A$$ مجموعهای از «قیود» (Constraints) تعریف میشوند؛ قیود، «برابریها» (Equalities) یا «نابرابریهایی» (Inequalities) هستند که تمامی اعضای مجموعه $$A$$ باید آنها را ارضا کنند. همچنین، به مجموعه $$A$$ یا همان دامنه یک تابع بهینهسازی مانند $$f$$ (به عبارت دیگر، دامنه تابع هدف مسأله بهینهسازی)، «فضای جستجو» (Search Space) یا «مجموعه انتخاب» (Choice Set) نیز گفته میشود.
با توجه به تعاریف انجام شده، هر یک از اعضای مجموعه $$A$$، یک جواب کاندید یا جواب امکانپذیر برای تابع بهینهسازی $$f$$ محسوب میشوند. تابع بهینهسازی $$f$$ با نامهای دیگری نظیر «تابع هدف» (Object Function)، «تابع زیان» (Loss Function) یا «تابع هزینه» (Loss Function)، «تابع برازندگی» (Fitness Function) و در برخی رشتههای خاص، «تابع انرژی» (Energy Function) شناخته میشود. تابع زیان و تابع هزینه برای مسائل کمینهسازی و تابع هدف، برای مسائل بیشینهسازی مورد استفاده قرار میگیرند.
به یک جواب کاندید یا امکانپذیر، که تابع هدف مسأله بهینه سازی را بیشینه یا کمینه کند، «جواب بهینه» (Optimal Solution) گفته میشود. همانطور که پیش از این نیز اشاره شد، مسائل بهینه سازی در ریاضیات، معمولا در قالب مسائل «کمینهسازی» (Minimization) نمایش داده میشوند.
کمینه محلی (Local Minimum)، بیشینه محلی (Local Maximum) و بهینه سراسری (Global Optimum)
یک کمینه محلی $$X^{\star}$$ تابع $$f$$، عنصری است که به ازاء آن پارامتری مانند $$\delta > 0$$ وجود دارد، به طوری که:
,$$\forall X \in A \; w h e r e \parallel X - X ^ { \star }\parallel \leq \delta$$
و به ازاء تمامی مقادیر $$X$$ که قید (Constraint) بالا را ارضا میکنند، عبارت $$f ( X ^ { \star } ) \leq f ( X )$$ برقرار است. به عبارت دیگر در برخی نواحی اطراف $$X^{\star}$$، تمامی مقادیر تابع $$f$$، بزرگتر یا برابر با مقدار عنصر کمینه محلی هستند. همچنین، بیشینه محلی به صورت مشابه و به شکل زیر تعریف میشود:
یک بیشینه محلی $$X^{\star}$$ تابع $$f$$، عنصری است که به ازاء آن پارامتری مانند $$\delta > 0$$ وجود دارد، به طوری که:
,$$\forall X \in A \; w h e r e \parallel X - X ^ { \star }\parallel \leq \delta$$
و به ازاء تمامی مقادیر $$X$$ که قید (Constraint) بالا را ارضا میکنند، عبارت $$f ( X ^ { \star } ) \geq f ( X )$$ برقرار است. به عبارت دیگر در برخی نواحی اطراف $$X^{\star}$$، تمامی مقادیر تابع $$f$$، کوچکتر یا برابر با مقدار عنصر بیشینه محلی هستند.
بهینه سازی محدب و غیر محدب
اگرچه عناصر کمینه یا بیشینه محلی بهتر از (یا حداقل برابر با) عناصر همسایگی اطرافشان هستند، ولی یک عنصر بیشینه یا کمینه سراسری (یا همان مقدار بهینه سراسری (Global Optimum)) از تمامی جوابهای کاندید یا امکانپذیر برای یک مسأله بهینه سازی بهتر خواهد بود. به طور کلی، تنها در صورتی که تابع هدف مسأله بهینه سازی «محدب» (Convex) نباشد، ممکن است بیش از یک «کمینه محلی» (Local Minimum) یا «بیشینه محلی» (Local maximum) در مسأله وجود داشته باشد.
در مسائل «بهینه سازی محدب» (Convex Optimization)، در صورتی که یک جواب بیشینه محلی یا کمینه محلی برای مسأله وجود داشته باشد، این جواب، بهینه سراسری مسأله مورد نظر نیز خواهد بود. با این حال، در یک مسأله بهینه سازی «غیر محدب» (Non-Convex) ممکن است بیش از یک جواب بیشینه محلی یا کمینه محلی وجود داشته باشد که لزوما همه آنها بهینه سراسری مسأله مورد نظر نخواهند بود.
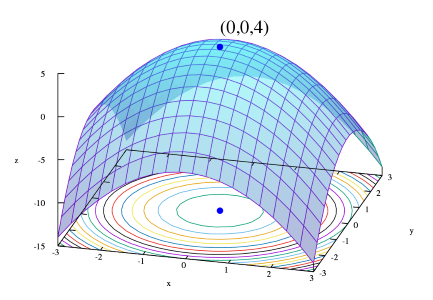
بسیاری از الگوریتمهایی که برای حل مسائل بهینه سازی غیر محدب پیشنهاد شدهاند (از جمله بسیاری از الگوریتمهای تجاری تولید شده برای حل مسائل بهینه سازی غیر محدب)، به خوبی قادر نیستند میان جوابهای بهینه محلی (بیشینه محلی یا کمینه محلی) و جوابهای بهینه سراسری (بیشینه سراسری یا کمینه سراسری) تمایز قائل شوند و تمامی جوابهای بهینه محلی یافت شده را به عنوان جواب واقعی مسأله بهینه سازی مورد نظر به شمار میآورند.
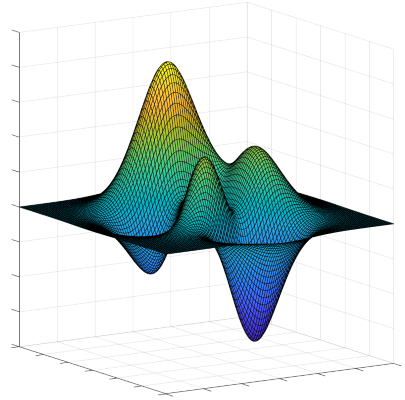
برای غلبه بر چنین معضلی در روشهای بهینه سازی، زیر شاخهای به نام «بهینه سازی سراسری» (Global Optimization) در حوزههای ریاضیات کاربردی و «آنالیز عددی» (Numerical Analysis) پدید آمده است. هدف روشهای بهینه سازی سراسری، پیادهسازی «الگوریتمهای قطعی» (Deterministic Algorithms) است که قادر هستند «همگرایی» (Convergence) به جواب بهینه سراسری واقعی یک مسئله بهینه سازی محدب را در زمان محدود تضمین کنند.
نمادگذاریها در بهینه سازی ریاضیاتی
در ادامه، مهمترین نمادگذاریها در بهینه سازی ریاضیاتی مورد بررسی قرار میگیرند.
مقدار کمینه یا بیشینه یک تابع
نمادگذاری زیر را در نظر بگیرید:
$$m i n _ { x \in R } ( x ^ { 2 } + 1 )$$
نمادگذاری نمایش داده شده، مقدار کمینه تابع هدف $$ x ^ { 2 } + 1$$ را، وقتی که مقدار $$x$$ از مجموعه اعداد حقیقی $$R$$ انتخاب شده باشد، نمایش میدهد. مقدار کمینه این تابع برابر با 1 (یک) است و در نقطه $$x=0$$ رخ میدهد. به طور مشابه، نمادگذاری زیر:
$$m a x _ { x \in R } \; (2 x)$$
مقدار بیشینه تابع هدف $$(2 x)$$ را نمایش میدهد. در این تابع، پارامتر $$x$$ میتواند هر مقدار حقیقی به خود بگیرد. در این حالت، از آنجایی که تابع هدف «بیکران» (Unbounded) است، هیچ مقدار بیشینهای برای آن وجود نخواهد داشت. به عبارت دیگر، جواب این مسأله «بینهایت» (Infinity) یا «تعریف نشده» (Undefined) است.
آرگومانهای ورودی بهینه (Optimal Input Argument)
نمادگذاری زیر را در نظر بگیرید:
$$ a r g \;m i n _ { x \in \left ( -\infty , -1 \right] } ( x ^ { 2 } + 1 )$$
نمادگذاری که در ادامه مشاهده خواهید کرد، هیچ تفاوتی با نمادگذاری بالا ندارد:
$$ a r g \;m i n _ { x } ( x ^ { 2 } + 1 ), \; s u b j e c t \; to: { x \in \left ( -\infty , -1 \right] }$$
نمادگذاریهای نمایش داده شده، مقدار (یا مقادیر) آرگومان $$x$$ در بازه $$x \in \left ( -\infty , -1 \right]$$ را نشان میدهد؛ مقادیری که تابع هدف $$x ^ { 2 } + 1$$ را کمینهسازی میکنند. نکته مهم در مورد نمادگذاری تعریف شده برای مسأله بهینهسازی بالا این است که در این نمادگذاری، مقادیر کمینه تابع هدف مشخص نشدهاند و تنها قید مرتبط با مقادیر ممکن برای آرگومان $$x$$ نمایش داده شده است. در این مورد، از آنجایی که مقدار صفر در مجموعه مقادیر امکانپذیر آرگومان $$x$$ وجود ندارد، مقدار کمینه این تابع در نقطه $$x=-1$$ حاصل میشود.
به طور مشابه، برای نمایش آرگومانهای ورودی بهینه یک مسأله بیشینهسازی، نمادگذاری زیر را در نظر بگیرید:
$$ a r g \;m a x _ { x \in \left [ -5 , 5 \right],\; y\in R } ( x \;cos \;y )$$
مانند حالت قبل، نمادگذاری که در ادامه مشاهده خواهید کرد، هیچ تفاوتی با نمادگذاری بالا ندارد:
$$ a r g \;m a x _ { x , \;y} ( x \; cos \;y), \; s u b j e c t\; t o : x \in \left [ -5 , 5 \right],\; y\in R$$
نمادگذاریهای نمایش داده شده، جفت مقادیر $$(x,y)$$ را نشان میدهند که مقدار تابع هدف $$x \; cos \;y$$ را بیشینه میکنند؛ در این تابع هدف، قید خاصی روی آرگومان $$x$$ تعریف شده است که بر اساس آن، تنها مقادیر موجود در بازه $$\left [ -5 , 5 \right]$$ قابل قبول هستند. مانند مورد قبلی، در نمادگذاری تعریف شده برای مسأله بیشینهسازی بالا، مقادیر بیشینه تابع هدف مشخص نشدهاند و تنها قیدهای مرتبط با مقادیر ممکن برای آرگومان $$x$$ و $$y$$ نمایش داده شدهاند. در این مورد، جفت مقادیر $$(x,y)$$ که به فرم $$ (5 , \; 2k\pi)$$ و $$ (-5 , \; (2 k + 1 ) \pi)$$ هستند، جوابهای این مسأله بهینهسازی هستند؛ پارامتر $$k$$ میتواند هر مقدار صحیحی را به خود بگیرد.
بنابراین، عملگرهای $$ a r g \;m i n$$ و $$ a r g \;m a x$$، به ترتیب بیانگر «آرگومان کمینه تابع هدف» (Argument of Minimum) و «آرگومان بیشینه تابع هدف» (Argument of Maximum) هستند و مشخص میکنند که مسأله مورد نظر، یک مسأله کمینهسازی است یا یک مسأله بیشینهسازی.
انواع مسائل بهینه سازی
همانطور که پیش از این نیز اشاره شد، گام دوم در فرایند بهینه سازی، مشخص کردن نوع و یا طبقهبندی مسألهای است که قرار است بهینهسازی شود. از آنجایی که هر یک از الگوریتمهای حل مسائل بهینه سازی (Optimization)، جهت یافتن مقادیر بهینه انواع خاصی از مسائل پیادهسازی میشوند، مشخص کردن «دستهبندی» (Classification) مدلهای بهینه سازی نقش مهمی در این فرایند ایفا خواهد کرد. در ادامه، برخی از مهمترین دستهبندیهای ارائه شده از مدلهای بهینه سازی نمایش داده خواهد شد.
مسائل بهینه سازی «پیوسته» (Continuous) و بهینه سازی «گسسته» (Discrete)
برخی از مدلهای بهینه سازی، جهت بهینه سازی توابعی طراحی شدهاند که متغیرهای آنها، مقادیر مجاز خود را از یک «مجموعه گسسته» (Discrete Set) اتخاذ میکنند (زیر مجموعهای از مقادیر صحیح)، در حالی که مدلهای دیگر، برای بهینه سازی توابعی پیادهسازی شدهاند که متغیرهای آنها میتوانند مقادیر حقیقی (Real Values) به خود بگیرند. به مدلهایی که از متغیرهای گسسته استفاده میکنند، مدلهای مسائل بهینه سازی گسسته (Discrete Optimization Problems) و به مدلهایی که برای بهینه سازی متغیرهای پیوسته مورد استفاده قرار میگیرند، مدلهای مسائل بهینه سازی پیوسته (Continuous Optimization Problems) گفته میشود.
حل کردن مسائل بهینه سازی پیوسته معمولا سختتر از حل مسائل بهینهسازی گسسته است؛ از آنجایی که سطح توابع پیوسته هموار (Smooth) هستند، این امکان وجود دارد که از توابع هدف و قیدهای تعریف شده برای مقادیر متغیرها در نقطه $$X$$، جهت استنتاج اطلاعات مرتبط با نقاط موجود در همسایگی این نقطه استفاده کرد و از این طریق، مقادیر بهینه مسأله بهینه سازی پیوسته را پیدا کرد.
با این حال، پیشرفتهای حاصل شده در توسعه الگوریتمهای بهینه سازی گسسته و افزایش قابل توجه قدرت محاسباتی سیستمهای کامپیوتری در چند سال اخیر سبب شده است تا الگوریتمهایی توسعه یابند که قادر هستند مسائل بهینه سازی گسسته بزرگ و پیچیده را به شکل بسیار کارآمدی حل کنند.
نکته مهم در مورد این دسته از مدلهای بهینه سازی این است که مدلهای پیوسته نقش مهمی در پیادهسازی مدلهای بهینه سازی گسسته دارند. زیرا، بسیاری از مدلهای بهینهسازی گسسته، مسائل بهینه سازی را به دنبالهای از زیر مسائل پیوسته (Continuous Subproblems) تقسیمبندی میکنند و برای حل کردن هر یک از این زیر مسائل، از مدل های بهینه سازی پیوسته استفاده میشود. بنابراین، یکی از مؤلفههای اساسی مدلهای بهینه سازی گسسته، روشهای حل مسائل بهینهسازی پیوسته هستند.
یکی از الگوریتمهایی که برای بهینه سازی مسائل پیوسته مورد استفاده قرار میگیرد، «الگوریتم بهینهسازی فاخته» (Cuckoo Optimization Algorithm) نام دارد. در ادامه، کدهای پیاده سازم این الگوریتم در زبان متلب نمایش داده شده است.
1clc, clear, close all
2%% Set problem parameters
3% select your cost function:
4costFunction = 'rastrigin'; % F6 +/-5.12
5npar = 100; % number of optimization variables
6varLo = -5; % Lower band of parameter
7varHi = 5; % Higher band of parameter
8%% Set COA parameters
9numCuckooS = 5; % number of initial population
10minNumberOfEggs = 2; % minimum number of eggs for each cuckoo
11maxNumberOfEggs = 4; % maximum number of eggs for each cuckoo
12maxIter = 100; % maximum iterations of the Cuckoo Algorithm
13knnClusterNum = 1; % number of clusters that we want to make
14motionCoeff = 9; % Lambda variable in COA paper, default=2
15accuracy = -inf; % How much accuracy in answer is needed
16maxNumOfCuckoos = 10; % maximum number of cuckoos that can live at the same time
17radiusCoeff = 5; % Control parameter of egg laying
18cuckooPopVariance = 1e-13; % population variance that cuts the optimization
19%% initialize population:
20cuckooPop = cell(numCuckooS,1);
21% initialize egg laying center for each cuckoo
22for cuckooNumber = 1:numCuckooS
23 cuckooPop{cuckooNumber}.center = ( varHi-varLo )*rand(1,npar) + varLo;
24end
25%% initialize COA cost minimization plot
26figure(1)
27hold on
28xlabel 'Cuckoo iteration'
29ylabel 'Cost Value'
30%% Start Cuckoo Optimization Algorithm
31iteration = 0;
32maxProfit = -1e20; % Let initial value be negative number
33goalPoint = (varHi - varLo)*rand(1,npar) + varLo; % a random goalpoint to start COA
34globalBestCuckoo = goalPoint;
35globalMaxProfit = maxProfit;
36profitVector = [];
37while ( (iteration <= maxIter) && (-maxProfit > accuracy) )
38
39 iteration = iteration + 1
40
41 % initialize number of eggs for each cuckoo
42 for cuckooNumber = 1:numCuckooS
43 cuckooPop{cuckooNumber}.numberOfEggs = floor( (maxNumberOfEggs - minNumberOfEggs) * rand + minNumberOfEggs );
44 end
45 % get total number of available eggs between all cuckooS
46 summ = 0;
47 for cuckooNumber = 1:numCuckooS
48 summ = summ + cuckooPop{cuckooNumber}.numberOfEggs;
49 end
50 % calculate egg laying radius for each Cuckoo, considering problem
51 % limitations and ratio of each cuckoo's eggs
52 for cuckooNumber = 1:numCuckooS
53 cuckooPop{cuckooNumber}.eggLayingRadius = cuckooPop{cuckooNumber}.numberOfEggs/summ * ( radiusCoeff * (varHi-varLo) );
54 end
55 % To lay eggs, we produced some radius values less than egg laying
56 % radius of each cuckoo
57 for cuckooNumber = 1:numCuckooS
58 cuckooPop{cuckooNumber}.eggLayingRadiuses = cuckooPop{cuckooNumber}.eggLayingRadius * rand(cuckooPop{cuckooNumber}.numberOfEggs,1);
59 end
60
61 for cuckooNumber = 1:numCuckooS
62 params = cuckooPop{cuckooNumber}.center; % get center values
63 tmpRadiuses = cuckooPop{cuckooNumber}.eggLayingRadiuses;
64 numRadiuses = numel(tmpRadiuses);
65 % divide a (hyper)circle to 'numRadiuses' segments
66 % This is to search all over the current habitat
67 angles = linspace(0,2*pi,numRadiuses); % in Radians
68 newParams = [];
69 for cnt = 1:numRadiuses
70 addingValue = zeros(1,npar);
71 for iii = 1:npar
72 randNum = floor(2*rand)+1;
73 addingValue(iii) = (-1)^randNum * tmpRadiuses(cnt)*cos(angles(cnt)) + tmpRadiuses(cnt)*sin(angles(cnt));
74 end
75 newParams = [newParams; params + addingValue ];
76 end
77
78
79 % check for variable limits
80 newParams(find(newParams>varHi)) = varHi;
81 newParams(find(newParams<varLo)) = varLo;
82 cuckooPop{cuckooNumber}.newPosition4Egg = newParams;
83 end
84
85 % Now egg laying is done
86
87 % Now that egg positions are found, they are laid, and so its time to
88 % remove the eggs on the same positions (because each egg only can go to one nest)
89 for cuckooNumber = 1:numCuckooS
90 tmpPopulation = cuckooPop{cuckooNumber}.newPosition4Egg;
91 tmpPopulation = floor(tmpPopulation * 1e20)/1e20;
92 ii = 2;
93 cntt = 1;
94 while ii <= size(tmpPopulation,1) || cntt <= size(tmpPopulation,1)
95 if all((tmpPopulation(cntt,:) == tmpPopulation(ii,:)))
96 tmpPopulation(ii,:) = [];
97 end
98 ii = ii + 1;
99 if ii > size(tmpPopulation,1) && cntt <= size(tmpPopulation,1)
100 cntt = cntt + 1;
101 ii = cntt + 1;
102 if ii > size(tmpPopulation,1)
103 break
104 end
105 end
106 end
107 cuckooPop{cuckooNumber}.newPosition4Egg = tmpPopulation;
108 end
109
110
111 % Now we evalute egg positions
112 for cuckooNumber = 1:numCuckooS
113 cuckooPop{cuckooNumber}.profitValues = -feval(costFunction,[cuckooPop{cuckooNumber}.center ; cuckooPop{cuckooNumber}.newPosition4Egg]);
114 end
115
116 % Now we check to see if cuckoo population is more than maxNumOfCuckoos
117 % this case we should keep 1st maxNumOfCuckoos cuckoos and kill the others
118 allPositions = [];
119 whichCuckooPopTheEggBelongs = [];
120 tmpProfits = [];
121 if numCuckooS > maxNumOfCuckoos
122 for cuckooNumber = 1:numCuckooS
123 tmpProfits = [tmpProfits; cuckooPop{cuckooNumber}.profitValues];
124 allPositions = [allPositions; [cuckooPop{cuckooNumber}.center; cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar)]];
125 whichCuckooPopTheEggBelongs = [whichCuckooPopTheEggBelongs; cuckooNumber*ones(size(cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar),1),1) ];
126 end
127 % now we sort cuckoo profits
128 [sortedProfits, sortingIndex] = sort(tmpProfits,'descend');
129 % Get best cuckoo to be copied to next generation
130 bestCuckooCenter = allPositions(sortingIndex(1),1:npar);
131
132 sortedProfits = sortedProfits(1:maxNumOfCuckoos);
133 allPositions = allPositions(sortingIndex(1:maxNumOfCuckoos),:);
134 clear cuckooPop
135 for ii = 1:maxNumOfCuckoos
136 cuckooPop{ii}.newPosition4Egg = allPositions(ii,:);
137 cuckooPop{ii}.center = allPositions(ii,:);
138 cuckooPop{ii}.profitValues = sortedProfits(ii);
139 end
140 numCuckooS = maxNumOfCuckoos;
141 else
142 for cuckooNumber = 1:numCuckooS
143 tmpProfits = [tmpProfits; cuckooPop{cuckooNumber}.profitValues];
144 allPositions = [allPositions; [cuckooPop{cuckooNumber}.center; cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar)] ];
145 whichCuckooPopTheEggBelongs = [whichCuckooPopTheEggBelongs; cuckooNumber*ones(size(cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar),1),1) ];
146 end
147 [sortedProfits, sortingIndex] = sort(tmpProfits,'descend');
148 % Get best cuckoo to be copied to next generation
149 bestCuckooCenter = allPositions(sortingIndex(1),1:npar);
150 end
151
152 maxProfit = sortedProfits(1);
153 currentBestCuckoo = bestCuckooCenter;
154 currentMaxProfit = -feval(costFunction,currentBestCuckoo);
155 if currentMaxProfit > globalMaxProfit
156 globalBestCuckoo = currentBestCuckoo;
157 globalMaxProfit = currentMaxProfit;
158 end
159
160 % Update cost minimization plot
161 plot(iteration, -globalMaxProfit,'ks','linewidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',10)
162 title([ 'Curent Cost = ' num2str(-globalMaxProfit) ' , at Iteration = ' num2str(iteration) ])
163 pause(0.01)
164
165 profitVector = [profitVector globalMaxProfit];
166
167 % ======== now we have some eggs that are safe and will grow up ==========
168 %========= mating: =============
169 % first we put all egg positions under each other
170 allPositions = [];
171 whichCuckooPopTheEggBelongs = [];
172 for cuckooNumber = 1:numCuckooS
173 allPositions = [allPositions; cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar)];
174 whichCuckooPopTheEggBelongs = [whichCuckooPopTheEggBelongs; cuckooNumber*ones(size(cuckooPop{cuckooNumber}.newPosition4Egg(:,1:npar),1),1) ];
175 end
176 if sum(var(allPositions)) < cuckooPopVariance
177 break
178 else
179 [clusterNumbers, clusterCenters] = kmeans(allPositions,knnClusterNum);
180 end
181 % make newly made clusters
182 cluster = cell(knnClusterNum,1);
183 for ii = 1:knnClusterNum
184 cluster{ii}.positions = [];
185 cluster{ii}.profits = [];
186 end
187
188 pointer = zeros(numel(cuckooPop),1);
189 for tmpCounter = 1:numel(cuckooPop)
190 nEggs = size(cuckooPop{tmpCounter}.newPosition4Egg,1);
191 pointer(tmpCounter) = nEggs;
192 end
193 for cnt = 1:length(clusterNumbers)
194 cluster{clusterNumbers(cnt)}.positions = [cluster{clusterNumbers(cnt)}.positions; cuckooPop{whichCuckooPopTheEggBelongs(cnt)}.newPosition4Egg(end-pointer(whichCuckooPopTheEggBelongs(cnt))+1,1:npar)];
195 cluster{clusterNumbers(cnt)}.profits = [cluster{clusterNumbers(cnt)}.profits; cuckooPop{whichCuckooPopTheEggBelongs(cnt)}.profitValues(end-pointer(whichCuckooPopTheEggBelongs(cnt))+1)];
196 pointer(whichCuckooPopTheEggBelongs(cnt)) = pointer(whichCuckooPopTheEggBelongs(cnt)) - 1;
197 end
198
199 % Determine the best cluster
200 f_mean = zeros(knnClusterNum,1);
201 for cnt = 1:knnClusterNum
202 f_mean(cnt) = mean(cluster{cnt}.profits);
203 end
204 [sorted_f_mean, sortingIndex_f_mean] = sort(f_mean,'descend');
205 maxFmean = sorted_f_mean(1); indexOfBestCluster = sortingIndex_f_mean(1);
206
207 % now that we know group with number 'indexOfBestCluster' is the best we
208 % should select their best point az Goal Point of other groups
209 [maxProfitInBestCluster, indexOfBestEggPosition] = max(cluster{indexOfBestCluster}.profits);
210 goalPoint = cluster{indexOfBestCluster}.positions(indexOfBestEggPosition,1:npar);
211
212 % now all other mature Cuckoos must go toward this goal point for laying
213 % their eggs
214 numNewCuckooS = 0;
215 for cntClstr = 1:size(cluster,1)
216 tmpCluster = cluster{cntClstr};
217 tmpPositions = tmpCluster.positions;
218 for cntPosition = 1:size(tmpPositions,1)
219 tmpPositions(cntPosition,:) = tmpPositions(cntPosition,:) + ...
220 motionCoeff * rand(1,npar) .* (goalPoint - tmpPositions(cntPosition,:));
221 end
222 % check if variables are in range
223 tmpPositions(find( tmpPositions>varHi )) = varHi;
224 tmpPositions(find( tmpPositions<varLo )) = varLo;
225 % update cluster positions
226 cluster{cntClstr}.positions = tmpPositions;
227 cluster{cntClstr}.center = mean(tmpPositions);
228 % update number of cuckoos: numCuckooS
229 numNewCuckooS = numNewCuckooS + size(cluster{cntClstr}.positions,1);
230 end
231 numCuckooS = numNewCuckooS;
232 % update cuckooPop
233 clear cuckooPop
234 cuckooPop = cell(numCuckooS,1);
235 cntNumCuckooS = 1;
236 for cnt = 1:size(cluster,1)
237 tmpCluster = cluster{cnt};
238 tmpPositions = tmpCluster.positions;
239 for cntPosition = 1:size(tmpPositions,1)
240 cuckooPop{cntNumCuckooS}.center = cluster{cnt}.positions(cntPosition,1:npar);
241 cntNumCuckooS = cntNumCuckooS + 1;
242 end
243 end
244 % Copy the Best cuckoo and its randomized form of this population to go
245 % to the next generation
246 currentBestCuckoo = bestCuckooCenter;
247 currentMaxProfit = -feval(costFunction,currentBestCuckoo);
248 if currentMaxProfit > globalMaxProfit
249 globalBestCuckoo = currentBestCuckoo;
250 globalMaxProfit = currentMaxProfit;
251 end
252 cuckooPop{end}.center = globalBestCuckoo; % This is because the best cuckoo will live longer and won't die right after egg laying
253 cuckooPop{end}.profitValues = -feval(costFunction,cuckooPop{end}.center);
254 tmp = rand(1,npar).*globalBestCuckoo;
255 tmp(find( tmp>varHi )) = varHi;
256 tmp(find( tmp<varLo )) = varLo;
257 cuckooPop{end-1}.center = tmp;
258 cuckooPop{end-1}.profitValues = -feval(costFunction,cuckooPop{end-1}.center);
259
260end % end of while
261%% Now Algorithm has stopped
262disp('Best Params = ')
263disp(globalBestCuckoo')
264fprintf('\n')
265disp('Cost = ')
266disp(-globalMaxProfit)
267% profit history is in: profitVector
268costVector = - profitVector;
269figure
270plot(costVector,'-ks','linewidth',3,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',15)
271xlabel 'Cuckoo Iteration'
272ylabel 'Cost Value'
273title(['Current Cost = ' num2str(costVector(end)) ', at iteration = ' num2str(iteration) ])تابع هدف Rastrigin:
1function y = rastrigin(x)
2y = 10.0 * size(x,2) + sum(x .^2 - 10.0 * cos(2 * pi .* x),2);مسائل بهینه سازی «مقید» (Constrained) و بهینه سازی «نامقید» (Unconstrained)
از یک جهت دیگر نیز میتوان میان مسائل و مدلهای بهینه سازی قائل شد: مسائلی که هیچ قیدی روی متغیرها تعریف نمیکنند و مسائلی که برای متغیرها قید تعریف میکنند. درصد قابل توجه از مسائلی که در جهان واقعی با آنها سروکار داریم، از نوع مسائل بهینه سازی نامقید هستند. در چند سال اخیر، مطالعات زیادی برای فرمولبندی دوباره (Re-Formulation) مسائل بهینه سازی نامقید در قالب مسائل بهینه سازی مقید ارائه شده است. در این مطالعات، از طریق جایگزین کردن قیدهای مسأله با «عبارات جریمه» (Penalty Terms)، یک مسأله بهینه سازی مقید به یک مسأله بهینه سازی نامقید تبدیل میشود.
مسائل بهینه سازی مقید مربوط به کاربردهایی هستند که در آنها قیدهای صریحی (Explicit Constraints) رو متغیرهای مسأله تعریف شده است. قیدهای تعریف شده روی این دسته از مثال میتوانند کرانهای (Bounds) ساده و یا سیستمهایی از معادلات و نامعادلات باشند که روابط میان متغیرهای مسأله را مدل میکنند.
پیش از ادامه این مبحث لازم است یادآور شویم که میتوانید بهینه سازی مقید را با استفاده از مجموعه آموزش بهینه سازی مقید فرادرس یاد بگیرید.
همچنین مسائل بهینهسازی مقید را میتوان بر اساس طبیعت قیدهای تعریف شده رو متغیرها (به عنوان نمونه، خطی، غیر خطی، محدب و سایر موارد) و هموار بودن توابع (به عنوان نمونه، مشتقپذیر (Differentiable) یا نامشتقپذیر (Non-Differentiable))، به طبقههای دیگری دستهبندی کرد.
مسائل بهینه سازی «قطعی» (Deterministic) و بهینه سازی «تصادفی» (Stochastic)
در مسائل بهینه سازی قطعی، فرض بر این است که دادههای مسأله داده شده به طور دقیق شناخته شده هستند. با این حال و به دلایل مختلفی، دادههای بسیاری از مسائل داده شده را به طور دقیق نمیتوان شناخت (یا در اختیار داشت). اولین دلیل برای در دسترس نبودن دادههای دقیق مسأله، «خطای اندازهگیری» (Measurement Error) دادهها است. دلیل دوم و بسیار مهم برای شناخته نبودن دادههای مسأله این واقعیت است که برخی از دادهها، اطلاعات مرتبط با آینده را نمایش میدهند (نظیر تقاضا برای یک محصول یا قیمت یک محصول در آینده) که نمیتوان با قطعیت (Certainty) آنها را شناخت.
در بهینه سازی همراه با عدم قطعیت (Optimization Under Uncertainty) یا بهینه سازی تصادفی (Stochastic Optimization)، عدم قطعیت در مدل ترکیب شده است. تکنیکهای «بهینه سازی استوار» (Robust Optimization) تنها زمانی میتوانند مورد استفاده قرار بگیرند که پارامترهای مسأله درون کرانهای مشخصی قرار گرفته باشند؛ در چنین حالتی، هدف پیدا کردن پیدا کردن جوابی است که به ازاء تمامی دادهها، امکانپذیر (یا قابل قبول) و به نحوی بهینه باشد.
مدلهای بهینه سازی تصادفی (Stochastic Optimization)، از این واقعیت که «توزیع احتمالی» (Probability Distribution) حاکم بر دادهها مشخص و یا قابل تخمین است، بهره میبرند؛ در چنین حالتی، هدف پیدا کردن یک سیاست (Policy) است که برای تمامی (یا تقریبا تمامی) نمونههای داده قابل قبول باشد و عملکرد مورد انتظار مدل (یا سیستم) را بهینه سازی کند.
مسائل بهینه سازی بدون هدف، تک هدفه و چند هدفه
بیشتر مسائل بهینهسازی، از یک تابع هدف برخوردار هستند. با این حال، مسائل بهینه سازی جالبی میتوان پیدا کرد که یا هیچ تابع هدفی ندارند و یا از چندین تابع هدف برخوردار هستند. «مسائل امکانپذیری» (Feasibility Problems) مسائلی هستند که در آنها، هدف پیدا کردن مقادیری برای متغیرها است که قیدهای مدل را ارضا کنند؛ در چنین حالتی مدل، تابع هدف خاصی ندارد که بخواهد آن را بهینه سازی کند. «مسائل مکملی» (Complementarity Problems)، مسائل بسیار فراگیری در مهندسی و اقتصاد محسوب میشوند؛ در چنین مواردی، هدف مدلهای بهینه سازی پیدا کردن جوابی است که «شرایط مکملی» (Complementarity Conditions) مسأله را ارضا کند.
«مسائل بهینه سازی چند هدفه» (Multi-Objective Optimization Problems) در بسیاری از حوزههای علمی و کاربردی نظیر مهندسی، اقتصاد و «لجستیک» (Logistics) کاربرد دارند و زمانی مورد استفاده قرار میگیرند که برای رسیدن به تصمیمات بهینه در سیستم، نیاز است میان دو یا چند «هدف متناقض» (Conflicting Objectives) موازنه برقرار شود. به عنوان نمونه، توسعه یک مؤلفه جدید ممکن است نیازمند کمینه کردن وزن و به طور همزمان، بیشینه کردن قدرت باشد. همچنین، جهت انتخاب سبد سرمایهگذاری مناسب باید به نحوی عمل کرد که بازگشت مورد انتظار سرمایه، بیشینه و ریسک سرمایه گذاری، کمینه گردد.
در عمل، برای بهینه سازی مسائل چند هدفه، از راهکارهایی استفاده میشود که در آنها، مسائل چند هدفه (Multi-Objective) به مسائل تک هدفه (Single-Objective) تبدیل میشوند؛ در این دسته از راهکارها، از طریق تشکیل یک ترکیب وزندار از توابع هدف مختلف و یا به وسیله جایگزین کردن توابع هدف با قیدهای مشخص، مسائل بهینه سازی چند هدفه به مسائل تک هدفه تبدیل میشوند.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای الگوریتمهای بهینهسازی هوشمند
- آموزش تئوری و عملی الگوریتمهای ژنتیک
- مجموعه آموزشهای هوش مصنوعی
- مجموعه آموزشهای الگوریتمهای ژنتیک و محاسبات تکاملی
- الگوریتم بهینهسازی فاخته — از صفر تا صد
- الگوریتم ژنتیک — از صفر تا صد
- الگوریتم کلونی مورچگان — از صفر تا صد
- الگوریتم کرم شب تاب — از صفر تا صد
^^










با سلام و عرض ادب
چند تا سوال داشتم
از گجا باید فهمید مدلی که طراحی کردیم بهینه و کارآمد است.
۲. در کد نویسی در مطلب از چه طریقی مشخص می شود محدودیت ها بدرستی انتخاب شده
۳. ما در الگوریتم می یایم از جواب موجه استفاده می کنیم از گجا بفهیم که جوابی که انتخاب کردیم موجه است چه سازگاری برای جواب موجه انجام دادهایم
سلام. خسته نباشین.
از برخی جملات این مقاله شما قصد دارم در مقاله خودم استفاده کنم. برای مرجع دهی خواستم راهنمایی بگیرم اگه از مقاله ای استخراج شده.
با سلام؛
برای استفاده از مطالب مجله فرادرس میتونید به «شرایط استفاده» در انتهای صفحه یا این لینک مراجعه کنید.
با تشکر از همراهی شما با مجله فرادرس
خیلی خوب بود. من تیکه هایی رو میخوام توی پایان نامه استفاده کنم. مرجع این مطالب رو میشه معرفی کنید. ممنون
با سلام؛
منابع تمامی مطالب مجله فرادرس، در انتهای مطلب و قبل از نام نویسنده قرار دارند.
با تشکر از همراهی شما با مجله فرادرس
عالی
استاد عزیز یک سوال داشتم
یک تفاوت بهینه یابی ریاضی آماری و بهینه یابی بر پایه الگوریتم تکاملی ؟
– چه جاهایی از هر کدام استفاده میشود؟
– سرعت کدامیک بیشتر است و سریعتر انجام میشود؟
– کدام فنی و دقیق است و نزدیکتر به بهینه میباشد؟
– توضیح دهید هر کدام به چه شکل کار میکند
امکانش هست راهنمایی بفرمائید
عالی بود بسیار جامع و کامل بود توضیحات.
سپاسگزارم
سلام. ابتدای این قسمت آموزشی این طور آمده که مطالب زیادی در مورد الگوریتم بهینه سازی بیزی در مجله فرادرس اومده. میشه بگید مطالب کجای مجله هستند من که هر چی گشتم چیزی ندیدم. متشکر
با سلام؛
از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم. از آنجا که در بهینهسازی بیزی برای نقاط یک احتمال پیشین میتوان در نظر گرفت، بر اساس بیز عمل و احتمال پسین را محاسبه کرد، مطالب مرتبط با آمار و احتمال بیزی به شما در فراگیری بهینهسازی بیزی کمک میکند.در این راستا، مطالعه مطالب زیر از مجله فرادرس به شما پیشنهاد میشود.
استنباط و آمار بیزی — به زبان ساده
قضیه بیز (Bayes Theorem) در احتمال شرطی و کاربردهای آن (+دانلود فیلم آموزش رایگان)
یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه
دسته بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها
قضیه بیز و کاربردهای آن – به زبان ساده (+ دانلود فیلم آموزش رایگان)
سری زمانی با رویکرد بیزی — راهنمای کاربردی
با احترام؛
شاد، پیروز و تندرست باشید.