قضیه بیز و کاربردهای آن – به زبان ساده

قبلاً نیز در بلاگ فرادرس به تفصیل در مورد قضیه بیز صحبت کرده‌ایم. اما در این نوشته از مجموعه نوشته‌های «ریاضیات به زبان ساده»، این قضیه مهم احتمالات را به بیانی بسیار ساده و عامه‌فهم توضیح خواهیم داد.

نکات مقدماتی

پیش از آن که وارد بحث اصلی بشویم، چند نکته هستند که به طور خیلی خلاصه ارائه کرده‌ایم:

• تست‌ها همان رویداد نیستند: وقتی که ما یک تست سرطان می‌دهیم، به این معنی نیست که سرطان واقعاً وجود دارد. وقتی که اسپم را تست می‌کنیم، بدین معنی نیست که واقعاً یک پیام اسپم داریم.
• تست‌ها کامل نیستند: تست‌ها در مواردی چیزهایی را تشخیص می‌دهند که واقعاً وجود ندارند (مثبت نادرست) و در برخی موارد نیز چیزهایی را که وجود دارند، تشخیص نمی‌دهند (منفی نادرست).
• تست‌ها، احتمال تست را معین می‌کنند و نه احتمال واقعی: افراد در اغلب موارد نتایج تست را به صورت مستقیم در نظر می‌گیرند و احتمال بروز خطا در تست را لحاظ نمی‌کنند.
• موارد مثبت نادرست موجب انحراف نتایج می‌شوند: فرض کنید به دنبال چیزی واقعاً نادر (مثلاً 1 در میلیون) جستجو می‌کنید. حتی در یک تست خوب هم احتمال این که یک نتیجه مثبت واقعاً یک مثبت نادرست باشد، چیزی بین 999،999 مورد باقی مانده است.
• افراد مختلف اعداد طبیعی را ترجیح می‌دهند: بیان «100 در 10،000» به جای «1%» به افراد کمک می‌کند که با خطاهای کمتری با اعداد کار کنند و این حالت در مورد درصدهای چندگانه بیشتر نمود دارد. برای مثال «از میان 100 مورد، 80 تا تست مثبت بوده‌اند، بسیار مفهوم‌تر از این است که بگوییم 80% از 1% تست مثبت خواهند بود.»
• حتی علم نیز یک تست است: عبارت‌های علمی را از منظر فلسفی می‌توان تست‌های ذاتاً ناکامل پنداشت و با آن‌ها باید بر همین اساس برخورد کرد. باید تفاوت این که یک تست برای یک آزمایش شیمیایی یا یک پدیده انجام یافته و این که رویدادی از خود آن پدیده رخ داده است را متوجه باشیم. تست‌های ما و ابزار اندازه‌گیری، ضریبی از خطای ذاتی دارند.

کاربردهای قضیه بیز

قضیه بیز نتایج حاصل از تست‌ها را به احتمال‌های واقعی رویداد تبدیل می‌کند. با استفاده از قضیه بیز می‌توانید:

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

• خطاهای اندازه‌گیری را اصلاح کنید: اگر مقدار احتمال واقعی و شانس بروز مثبت نادرست و منفی نادرست را بدانید، می‌توانید خطاهای اندازه‌گیری را اصلاح کنید.
• احتمال واقعی را به احتمال اندازه‌گیری شده تست ارتباط دهید: قضیه بیز به ما امکان می‌دهد که (PR(A|X یعنی احتمال وقوع رویداد A را با فرض شرط X به (PR(X|A اتصال دهیم که شانس وقوع شرط X با فرض اتفاق افتادن رویداد A است. برای مثال با دانستن نتایج تست ماموگرافی و شناخت نرخ خطا می‌توانیم احتمال واقعی رخداد سرطان را تشخیص دهیم.

آناتومی یک تست

در ادامه یک سناریوی تست سرطان را بررسی می‌کنیم:

• 1% از زنان سرطان سینه دارند (و از این رو 99% ندارند)
• 80% از تست‌های ماموگرافی در صورت وجود سرطان می‌توانند آن را تشخیص دهند (و از این رو 20% نمی‌توانند آن را تشخیص دهند)
• 9.6% از تست‌های ماموگرافی در مواردی که سرطان وجود نداشته باشد، منجر به اعلام نتایج مثبت نادرست می‌شوند (و از این رو 90.4% مورد منفی را به درستی نشان می‌دهند)

اگر بخواهیم موارد فوق را در یک جدول تنظیم کنیم به صورت زیر خواهد بود:

این جدول را چطور می‌توانیم بخوانیم؟

• 1% از افراد سرطان دارند.
• اگر فرد سرطان داشته باشد، در ستون اول قرار دارد، احتمال این که نتیجه تست وی مثبت باشد 80% است. احتمال این که نتیجه تست منفی باشد برابر با 20% است.
• اگر سرطان نداشته باشد، در ستون دوم است. یعنی 9.6% احتمال هست که نتایج تست مثبت باشد و 90.4 درصد احتمال هست که نتایج تست منفی باشد.

این تست چقدر دقیق است؟

اینک فرض کنید نتیجه تست فرد مثبت است. احتمال این که او سرطان داشته باشد چقدر است؟80%؟، 99%؟ یا 1%؟

در ادامه این وضعیت را توضیح داده‌ایم:

• اگر نتیجه تست فرد مثبت باشد. این بدان معنی است که جایی در ردیف اول جدول فوق قرار دارد. در این مورد حدسی نمی‌زنیم، وضعیت وی می‌تواند یک مثبت درست یا یک مثبت نادرست باشد.
• احتمال یک مثبت درست یعنی احتمال این که شخص سرطان داشته باشد * احتمال این که تست به درستی تشخیص داده باشد، برابر با 1% * 80% = 0.008 است.
• احتمال یک مثبت نادرست یعنی احتمال این که سرطان نداشته باشد * احتمال این که تست، آن را تشخیص داده باشد، برابر با 99% * 9.6% = 0.09504 است.

اگر نتایج فوق را در جدولی تنظیم کنیم، به صورت زیر خواهد بود:

سؤالی که اینجا پیش می‌آید این است که وقتی نتیجه تست فرد مثبت است، احتمال این که سرطان داشته باشد، چه قدر است؟ احتمال یک رویداد از تقسیم تعداد راه‌هایی که ممکن است رخ بدهد بر همه خروجی‌های ممکن به دست می‌آید:

 همه حالت‌ها/ رویداد مطلوب = احتمال

احتمال این که فردی واقعاً یک نتیجه مثبت داشته باشد برابر با 0.008 است. احتمال این که هر گونه نتیجه مثبتی داشته باشد، برابر است با احتمال یک مثبت درست به علاوه احتمال مثبت نادرست یعنی (0.008 + 0.09504 = 0.10304)

بنابراین احتمال وجود سرطان در صورت مثبت بودن نتیجه برابر خواهد بود با 0.008/0.10304 = 0.0776 یا در حدود 7.8 درصد.

نتایج تست

نتیجه فوق بسیار جالب است چون نشان می‌دهد که اگر نتیجه تست ماموگرافی مثبت باشد، احتمال این که فرد واقعاً سرطان داشته باشد، تنها در حدود 7.8 درصد است و نه 80 درصد که میزان دقت تصور شده برای تست است. این نتیجه ممکن است در ابتدا تا حدودی عجیب به نظر برسد، چون تست در 9.6 درصد موارد، نتایج مثبت نادرستی ارائه می‌کند که بسیار بالا است. از این رو موارد مثبت نادرست زیادی در هر جمعیتی وجود خواهند داشت. در مورد بیماری‌های نادر، اغلب نتایج تست مثبت نادرست خواهند بود.

با نگاهی گذرا به جدول می‌توانیم نکته مهمی را متوجه شویم. اگر 100 نفر را انتخاب کنید، تنها 1 نفر سرطان خواهد داشت (1%) و احتمال مثبت بودن تست وی نیز بالا است (80%). از میان 99 فرد باقی مانده در حدود 10 درصد، پاسخ تستشان مثبت خواهد بود و از این رو 10 مورد مثبت نادرست داریم. با در نظر گرفتن همه موارد مثبت تنها 1 مورد از میان 11 مورد درست است، بنابراین وقتی پاسخ تست سرطان مثبت باشد، احتمال وجود سرطان تنها 1/11 است. عدد دقیق 7.8 درصد% است که کاملاً نزدیک به مقدار 1/13 است که در بخش فوق محاسبه کردیم. می‌بینید که بدون محاسبه توانسته‌ایم تخمین معقولی به دست آوریم.

قضیه بیز

ما می‌توانیم فرایند فوق را به صورت یک معادله بنویسیم. این معادله قضیه بیز نام دارد. به طور خیلی خلاصه، قضیه بیز این امکان را فراهم می‌سازد که نتایج تست را دریافت کنید و انحرافی که موارد مثبت نادرست در آن ایجاد می‌کند از آن جدا سازید. بدین ترتیب احتمال واقعی رخداد یک واقعه را پیدا می‌کنید. معادله این قضیه چنین است:

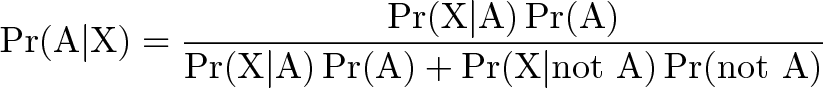
توضیح معادله فوق چنین است:

• (PR(A|X احتمال داشتن سرطان (A) با فرض مثبت بودن تست (X) است. چیزی که می‌خواهیم بدانیم این است که با این نتیجه مثبت احتمال این که واقعاً فرد سرطان داشته باشد چه قدر است؟ در مثال ما پاسخ 7.8 درصد است.
• (PR(X|A احتمال داشتن تست مثبت است (X) با فرض وجود سرطان (A) است. این احتمال وجود یک مثبت درست است که در مثال ما 80% است.
• (PR(A احتمال داشتن سرطان است (1%)
• (PR(NOT A احتمال نداشتن سرطان است (99%)
• (PR(X|NOT A احتمال تست مثبت (X) با فرض عدم وجود سرطان (~A) است. این همان حالت مثبت نادرست است که در مورد ما برابر با 9.6 درصد است.

قضیه بیز به زبان ساده

قضیه بیز را می‌توان به صورت احتمال یک نتیجه مثبت درست تقسیم بر احتمال هر نتیجه مثبت نیز بیان کرد. معادله آن به طور زیر ساده می‌شود:

(PR(X ثابت نرمال‌سازی است و به مقیاس بندی معادله کمک می‌کند. بدون وجود این جمله ممکن است فکر کنید که نتایج مثبت تست، احتمال 80% برای داشتن سرطان ایجاد می‌کنند.

(PR(X به ما می‌گوید که احتمال داشتن هر نوع نتیجه مثبتی، چه مثبت واقعی در جمعیت سرطانی (1%) و چه مثبت نادرست در جمعیت غیر سرطانی (99%) چه مقدار است. این وضعیت تا حدودی شبیه میانگین وزن‌دار است و به مقایسه احتمال کلی یک نتیجه مثبت کمک می‌کند.

در مثال ما (PR(X بسیار بزرگ است، زیرا احتمال رخداد مثبت نادرست زیاد است. به لطف ثابت نرمال‌سازی می‌توانیم این اختلاف را تعدیل کنیم. این بخشی است که اغلب افراد فراموش می‌کنند و باعث می‌شود که نتیجه 7.8 درصد برای ذهنشان عجیب و غیر شهودی باشد.

درک شهودی قضیه بیز

در این مقاله تلاش کرده‌ایم تا به جز معادلات ریاضی و بحث‌های احتمالاتی در شما درکی شهودی از مفهوم قضیه بیز ایجاد کنیم. قیاس باعث تفهیم می‌شود؛ اما برای ایجاد این تفهیم به هزاران کلمه نیاز است.

یک جمعیت واقعی را تصور کنید. برخی تست‌ها را روی آن‌ها امتحان کنید تا از طریق این جمعیت واقعی درک خود را عمیق‌تر کنید و نتایج تست را به دست آورید. اگر درک صحیحی به دست آورده باشید، احتمال‌های تست و احتمال‌های واقعی با هم منطبق خواهند بود. هرکس که نتایج تستش مثبت باشد، واقعاً مثبت است و هر کس که نتایج تستش منفی باشد، واقعاً منفی است.

فیلم آموزش نظریه صف Queueing theory در فرادرس

کلیک کنید

اما ما در دنیای واقعی زندگی می‌کنیم. تست‌ها ممکن است خطا کنند. برخی اوقات افرادی که سرطان دارند در تست‌ها مشخص نمی‌شوند و یا برعکس.

قضیه بیز به ما امکان می‌دهد که انحراف نتایج تست را اصلاح کنیم و جمعیت اولیه را از نو ایجاد کرده و احتمال واقعی یک نتیجه مثبت واقعی را محاسبه کنیم.

فیلترینگ با استفاده از قضیه بیز

یکی از کاربردهای هوشمندانه قضیه بیز در فیلترینگ اسپم است. فرض کنید شروط زیر برقرار باشند:

• رویداد A: یک پیام، اسپم است
• تست X: پیام حاوی عبارت خاصی است (X).

اگر بخواهیم موارد فوق را در یک فرمول خوانا جمع‌بندی بکنیم:

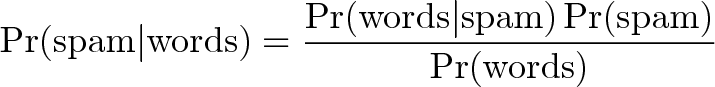
فیلترینگ بیزی به ما امکان می‌دهد که احتمال اسپم بودن واقعی یک پیام را با فرض نتایج تست (وجود کلمات خاص) به دست آوریم. بدیهی است که کلماتی مانند «ویاگرا» نسبت به پیام‌های معمولی، احتمال حضور بالاتری در پیام‌های اسپم دارند.

فیلترینگ اسپم بر اساس فهرست سیاه، روشی ناکامل است، چون بسیار محدودکننده است و موارد مثبت نادرست بسیار زیاد هستند. اما فیلترینگ بیزی به ما امکان می‌دهد که از احتمالات کمک بگیریم. زمانی که مشغول تحلیل کلمات داخل یک پیام هستیم، می‌توانیم احتمال اسپم بودن آن را (به جای یک تصمیم‌گیری بله/خیر) محاسبه کنیم. اگر پیامی دارای احتمال 99.9% اسپم بودن باشد، احتمالاً اسپم است. به مرور که فیلتر ما با پیام‌های بیشتر و بیشتر آموزش می‌بیند، احتمال این که کلمات خاصی معرف پیام‌های اسپم باشند را به‌روزرسانی می‌کند. فیلترهای بیزی پیشرفته می‌توانند چندین کلمه را با هم تحلیل کنند.

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز بررسی کنید:

• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش ششم: الگوریم بیز ساده
• مجموعه آموزش‌های نرم‌افزارهای آماری‎
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• قضیه بیز در احتمال شرطی و کاربردهای آن
• مجموعه آ؛موزش های آمار، احتمالات و داده‌کاوی

==