نظریه آمار — مفاهیم و کاربردها

تئوری یا نظریه آمار، پایه‌های اصلی برای تکنیک‌های تحلیل داده‌ها و مطالعات میدانی است که از آمار به عنوان ابزار اصلی تحقیق استفاده می‌کنند. نظریه آمار از برآوردیابی تا استنباط و نظریه تصمیم گسترده است. بخش اعظم و مهم در نظریه آمار، مربوط به آمار ریاضی (Mathematical Statistics) است که در آن به کمک نظریه احتمال و روش‌های بهینه‌سازی، امکان انجام استنباط آماری بوجود می‌آید. آمار توصیفی، آمار استنباطی، تحلیل‌های چند متغیره و مدل‌های خطی از بخش‌های کاربردی نظریه آمار هستند.

تمامی ابزارهای آمار کاربردی، توسط نظریه آمار پوشش داده شده و پایه اصلی همه این تکنیک‌ها محسوب می‌شود. در این نوشتار قصد داریم خوانندگان را با تئوری یا نظریه آمار آشنا کرده و کاربردهای آن را یادآوری کنیم.

به منظور کسب اطلاعات بیشتر در مورد اصطلاحات به کار رفته در این نوشتار بهتر است ابتدا مطالب جامعه آماری — انواع داده و مقیاس‌های آن‌ها و روش‌ های نمونه‌گیری (Sampling) در آمار — به زبان ساده را بخوانید. همچنین مطالعه متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات نیز مفید خواهد بود.

نظریه آمار چیست؟

روش‌ها و ابزارهای آماری همگی ریشه در نظریه آمار (Statistics Theory) دارند. در حقیقت نظریه آمار، علمی است که به جمع‌آوری داده‌ها، تلخیص و خلاصه‌سازی آن‌ها و همچنین استنباط و شناخت رفتار آن‌ها دلالت داشته و در این بین ابزارهایی را برای چنین منظور‌هایی ارائه می‌دهد.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

شاید بتوان نظریه آمار را به بخش‌های مختلفی تقسیم‌بندی کرد. این بخش‌ها به صورت فهرست‌وار در ادامه دیده می‌شوند.

• مدل آماری
• جمع‌آوری داده
• محاسبه شاخص‌های آماری
• توصیف داده
• استنباط آماری-کاربردی

در قسمت‌های بعدی این نوشتار، هر یک از بخش‌ها را معرفی و کاربردهایشان را تشریح خواهیم کرد.

ایجاد مدل

مدل آماری سعی در توصیف جامعه آماری دارد. در این بین ابزارهایی نیز در خدمت تکنیک‌های مدل‌سازی قرار گرفته است:

• نمونه‌گیری (Sampling) از یک جامعه متناهی.
• اندازه‌گیری و تخمین خطای مشاهداتی یا نمونه‌گیری به منظور بهبود روش‌های آماری
• مطالعه روابط بین متغیرهای جامعه آماری

مدل‌های ایجاد شده توسط روش‌های آماری، توسط تکنیک‌های آزمون فرض، مورد ارزیابی قرار گرفته و پارامترهای آن‌ها بازبینی می‌شوند. البته روش‌هایی دیگری نیز برای اندازه‌گیری کارایی مدل‌های ایجاد شده، نیز وجود دارد که مانع بوجود آمدن بیش‌برازش (Overfitting) یا کم‌برازش (Underfitting) شود.

معمولا ارزیابی مدل ایجاد شده و تنظیم پارامترهای آن را به کمک روش‌های اعتبارسنجی متقابل (Cross-Validation) انجام می‌دهند.

جمع‌آوری داده

روش‌های مختلفی برای جمع‌آوری داده در نظریه آمار مطرح شده است. هر یک از این تکنیک‌ها با توجه به شرایط جامعه آماری، سعی در کسب بیشترین اطلاعات از داده را دارد، بطوری که اریبی یا گرایش در بین مقادیر جمع‌آوری شده وجود نداشته و خطای مشاهداتی به حداقل برسد.

بهینه‌سازی و اطمینان از فرآیند جمع‌آوری داده‌ها، هزینه‌های طرح‌های آماری را کاهش داده و در عوض نتایج استنباط آماری را قوت می‌بخشند. این کار معمولا توسط محورهای زیر صورت می‌گیرد:

• طرح آزمایشات به منظور برآورد اثر تیمارها یا انجام آزمون فرض آماری.
• بررسی نمونه‌ای برای توصیف جامعه آماری.

محاسبه شاخص‌های آماری

محاسبه شاخص‌های آماری قسمتی از تحلیل آماری است که به وظیفه توصیف جامعه آماری یا نمونه برآمده از آن می‌پردازد. به همین دلیل گاهی این بخش از فرآیند تجزیه و تحلیل آماری را آمار توصیفی (Descriptive Statistics) می‌گویند.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

در این بین ویژگی‌های جامعه آماری و همچنین نوع متغیرها، مشخص می‌کند که چه نوع محاسباتی برای آمار توصیفی لازم است.

از طرفی انتخاب توزیع آماری مناسب برای داده‌ها (کشف یا آزمون) از طریق جدول فراوانی (Frequency Table) یا نمودارهای فراوانی، برای نمایش توزیع احتمالی (Probability Distribution) مشاهدات در نمونه یا جامعه آماری بسیار مناسب است.

شاخص‌های توصیفی مانند ضرایب همبستگی نمونه‌ای، امکان بررسی و سنجش میزان ارتباط بین دو یا چند متغیر را فراهم می‌آورد.

اغلب نرم‌افزارهای آماری نظیر SPSS, SAS یا زبان‌های برنامه‌نویسی محاسبات آماری مانند R، امکان محاسبات چنین شاخص‌های آماری مانند شاخص‌های مرکزی (Central Tendency) همچون «میانگین» (Mean)، «نما» (Mode) و میانه (Median)، شاخص‌های پراکندگی (Dispersion Index) مانند «دامنه تغییرات» (Range)، «واریانس» (Variance) و «انحراف معیار» (Standard Deviation) همچنین شاخص‌های تقارن (Symmetrical Index) مانند «چولگی» (Skewness) و «کشیدگی» (Kurtosis) را دارند.

توصیف داده

تئوری یا نظریه آمار وظیفه تعیین سوالات و همچنین پاسخ‌هایی را دارد که یک محقق در زمینه داده جمع‌آوری شده خواهد داشت. این موضوعات جدا از استنباط آماری محسوب می‌شود. برخی از این تکنیک‌ها در ادامه مشخص شده‌اند.

• خلاصه‌سازی ویژگی‌های جامعه آماری به شکل تابع توزیع احتمال (Probability Distribution Function) یا تابع توزیع احتمال تجمعی (Cumulative Distribution Function).
• نمایش رابطه بین متغیرهای مستقل و وابسته به وسیله تکنیک و تحلیل‌های رگرسیونی (Regression Analysis).
• تعیین روش‌هایی برای پیش‌بینی نتایج یک آزمایش تصادفی به شرط پیش‌آمدهای دیگر به کمک احتمال شرطی (Conditional Probability).
• تکنیک‌های کاهش ابعاد یک مسئله پیچیده، به کمک کم کردن تعداد متغیرهای مدل آماری (Dimension Reduction) با کمترین اطلاعات از دست رفته.

در نظریه آمار و به کمک قوانین احتمال و توزیع‌های مختلف جوامع آماری، راه برای برآورد پارامترها و همچنین انجام آزمون یا ایجاد فاصله اطمینان برای آن‌ها در گام بعدی یعنی استنباط آماری فراهم می‌شود.

فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS در فرادرس

کلیک کنید

انواع روش‌های برآوردیابی و همچنین تعیین خصوصیات بهینه برای برآوردگرها باعث بوجود آمدن دسته‌های مختلف از آن‌ها شده که بنا به شرایط مسئله، محقق از تکینک‌های برآوردیابی مشخصی استفاده می‌کند.

در این بین طرح آزمایش (Experimental Design) و تعیین راه‌کاری برای انتخاب یا تولید داده‌های تصادفی (Planned Randomize generation of data)، بطوری که بیشترین اطلاعات از جامعه آماری توسط نمونه جمع‌آوری شود، در صحت نتایج و قابلیت تعمیم آن‌ها به جامعه آماری نقش مهمی ایفا می‌کند.

استنباط آماری-کاربردی

نظریه آمار، پایه رویکردهای مختلف آمار استنباطی نیز هست. آمار استنباطی شامل روش‌هایی است که به واسطه آن‌ها، براساس نمونه، جامعه آماری شناخته شده و فرضیاتی در مورد آن یا پارامترهایش مورد آزمون قرار می‌گیرد.

جنبه‌های مختلفی برای استنباط آماری وجود دارد:

• برآورد نقطه‌ای (Point Estimation) پارامترهای جامعه آماری.
• برآورد فاصله‌ای (Interval Estimation) یا فاصله اطمینان برای پارامترهای جامعه آماری.
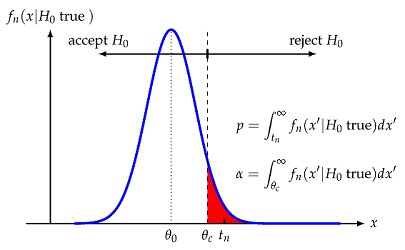
• آزمون فرض آماری (Statistical Hypothesis Testing).

بسیاری از روش‌های آماری براساس فرض‌های آماری پایه‌ریزی شده‌اند که باعث می‌شود یک محقق با توجه به شرایط مسئله و داده‌ها، برای تجزیه و تحلیل اطلاعات جمع‌آوری شده یکی از آن‌ها را انتخاب کند. این شرایط در تکنیک‌ها و روش‌های پارامتری (Parametric Statistics) مورد نظر قرار می‌گیرند.

البته روش‌های استوار و قدرتمند آماری نیز وجود دارند که با در نظر گرفتن شرایط ضعیف‌تر امکان تحلیل داده‌ها را فراهم می‌آورند. معمولا چنین تکنیک‌هایی مربوط به روش‌های ناپارامتری (Non-Parametric Statistics) هستند.

خلاصه و جمع‌بندی

در این نوشتار به جنبه‌های مختلف نظریه آمار و کاربردهای آن در حل مسائل تحلیل داده‌ها پرداختیم. از بخش‌های مهم نظریه آمار می‌توان به تئوری نمونه‌گیری (Sampling)، تئوری احتمال (Probability Theory) و نظریه توزیع‌ احتمال (Distribution Theory) اشاره کرد. در حقیقت همه این تئوری‌ها و نظریه‌ها، ساختارهای اصلی تئوری یا نظریه آمار محسوب شده و تکنیک‌هایی تحلیل‌های آماری را پایه‌ریزی می‌کنند.