خواص کولیگاتیو محلول ها — به زبان ساده

در علم شیمی، خواص کولیگاتیو به خواصی از محلول‌ها گفته می‌شود که وابسته به نسبت تعداد ذرات حل‌شونده به تعداد مولکول‌های حلال در محلول هستند. خواص یک محلول، از خواص حلال یا حل‌شونده خالص، متفاوت است. بسیاری از خواص محلول‌ها وابسته به ماهیت شیمیایی حل‌شونده آن‌ها است. در مقایسه با آب، محلول هیدروژن کلرید، خاصیت اسیدی بیش‌تر و محلولی از آمونیاک، خاصیت بازی بیش‌تری دارد. همچنین، محلولی از سدیم کلرید، چگالی بیش‌تر و محلول آب و شکر، ویسکوزیته بیش‌تری خواهد داشت.

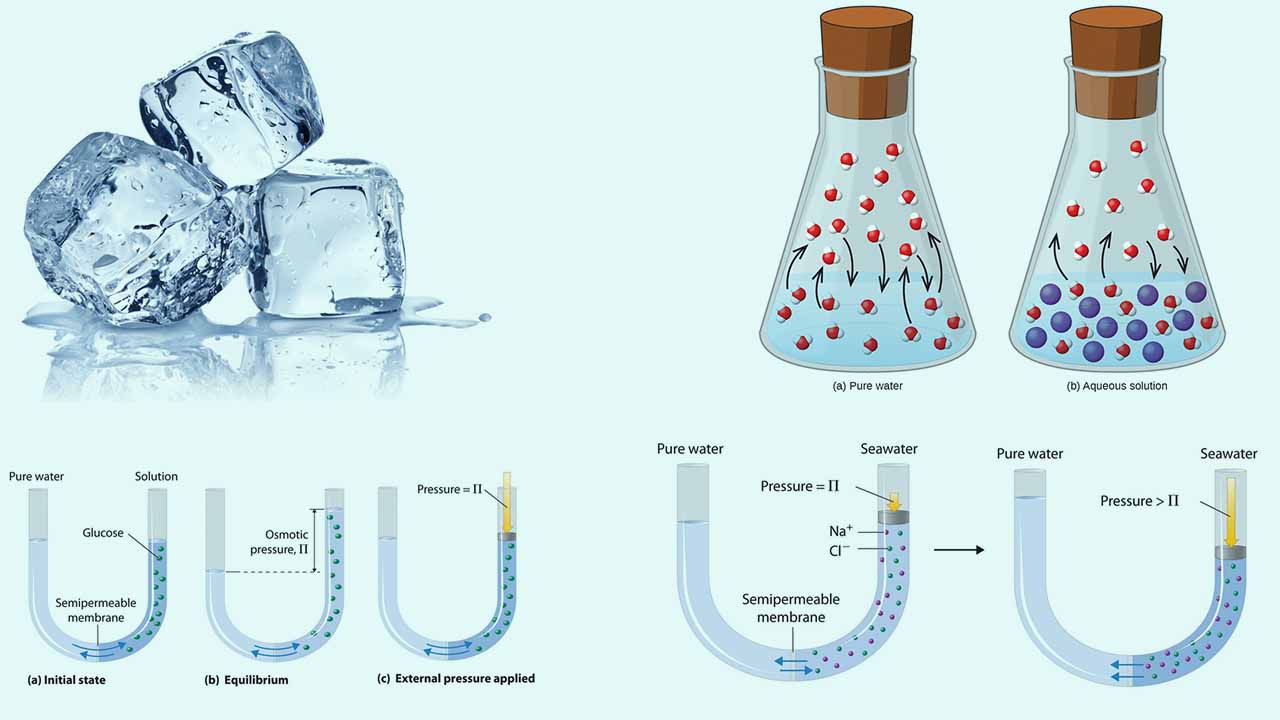
برخی از خواص در محلول‌ها وجود دارند که تنها به غلظت کلی ذرات حل‌شونده مرتبط هستند و ارتباطی با ماهیت این مواد ندارند. به این خواص، خواص کولیگاتیو می‌گویند که شامل موارد زیر است:

• نزول فشار بخار
• افزایش نقطه جوش
• نزول نقطه انجماد
• فشار اسمزی

فیلم آموزش شیمی فیزیک – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

در ادامه و پس از ارائه توضیح مختصری در خصوص مفهوم غلظت، به بررسی خواص کولیگاتیو محلو‌ل‌ها خواهیم پرداخت.

مولالیته و کسر مولی

برای بیان غلظت، از واحدهای مختلفی استفاده می‌شود. به طور مثال، از مولاریته در محاسبات استوکیومتری بهره می‌گیرند چراکه بر اساس مقادیر مولی ذرات حل‌شونده بنا شده است. از آن‌جایی که حجم محلول‌ها با دما تغییر پیدا می‌کنند، غلظت‌های مولی نیز به طور مشابه تغییر خواهند کرد. زمانی که از مولاریته در بیان غلظت کمک بگیریم، غلظت یک محلول در دماهای مختلف، به دلیل فرآیندهای انبساط و انقباض محلول، متفاوت خواهد بود. در محاسبات شامل خواص کولیگاتیو محلول‌ها، بهتر است از واحدهایی استفاده شود که مقادیر آن‌ها به دما وابسته نباشند. دو نوع از این واحدها عبارتند از: کسر مولی و مولالیته.

کسر مولی یک محلول $$(X)$$، به نسبت مقادیر مولی به تعداد کل‌ مول‌های اجزای محلول می‌گویند. با این تعریف، مجموع کسرهای مولی اجزای یک محلول، برابر با ۱ خواهد بود. مولالیته نیز به صورت نسبت تعداد مول‌های حل‌شونده به جرم حلال (بر حسب کیلوگرم) می‌گویند.

با توجه به این‌که واحدهای گفته شده، به کمک جرم و مقادیر مولی محاسبه می‌شوند، با دما تغییر نمی‌کنند و بنابراین، زمانی که به مقادیر غلظت، مستقل از دما احتیاج داشته باشیم، این واحدها بسیار مناسب خواهند بود.

مثال محاسبه کسر مولی و مولالیته

ضد یخ موجود در بیش‌تر خودروها، مخلوطی با حجم‌های برابر از اتیلن گلایکول و آب، به همراه مقادیر کمی از سایر مواد برای جلوگیری از خوردگی است. مولالیته و کسر مولی اتیلن گلایکول با فرمول $$C _ 2 H _ 4 (O H )_ 2$$ را در محلولی شامل $$2.22 \times 10 ^ {23}$$ اتیلن گلایکول و $$2 \times 10 ^ {3}$$ آب (در حدود ۲ لیتر آب و ۲ لیتر اتیلن گلایکول) حساب کنید.

کسر مولی اتیلن گلایکول را در ابتدا به کمک بدست آوردن مقادیر مولی هر دو جزء محلول و جایگذاری آن‌ها در تعریف کسر مولی بدست می‌آوریم.

$$\begin {equation} \begin {array}{c} \mathrm {mol} \mathrm {C}_{2} \mathrm {H}_{4}( \mathrm {O H})_{2}=2.22 \times 10^{3} \mathrm {g} \times \frac{1 \mathrm {mol} \mathrm {C}_{ 2} \mathrm {H}_{4}( \mathrm { O H}) _{2}}{62.07 \mathrm {g} \mathrm{C }_{2} \mathrm {H}_{4} (\mathrm { O H})_{2}}= 35.8 \mathrm{mol} \mathrm{ C}_{2} \mathrm { H}_ {4}( \mathrm{ O H })_{2} \\ \mathrm {mol} \mathrm{ H}_{2} \mathrm {O}=2.00 \times 10^{3} \mathrm {g} \times \frac{1 \mathrm {mol} \mathrm {H}_{2} \mathrm {O}} {18.02 \mathrm{g} \mathrm{ H}_{2} \mathrm {O}}=111 \mathrm {mol} \mathrm {H}_{2} \mathrm{ O} \\ X_{\text {ethylene glycol }}=\frac{ 35.8 \mathrm {mol} \mathrm {C}_{2} \mathrm {H}_{4}(\mathrm {OH})_{2}}{(35.8+111) \mathrm{ mol} \text { total }}=0.244 \end {array} \end {equation}$$

توجه داشته باشید که کسر مولی یک خاصیت بدون بعد است. برای محاسبه مولالیته، باید تعداد مول حل‌شونده و جرم حلال را به کیلوگرم داشته باشیم. در ابتدا، از جرم داده شده اتیلن گلایکول و جرم مولی آن برای پیدا کردن جرم حل‌شونده استفاده می‌کنیم.

$$\begin {equation} 2.22 \times 10^{3} \mathrm {g} \mathrm { C } _ {2} \mathrm {H}_{4}( \mathrm{O H } )_{2} \left (\frac {\mathrm {mol} \mathrm { C } _ {2} \mathrm { H }_{2}(\mathrm {O H})_{2}}{62.07 \mathrm {g}}\right)=35.8 \mathrm {mol} \mathrm {C}_{2} \mathrm {H}_{4}(\mathrm {O H})_{2} \end {equation}$$

در ادامه نیز جرم آب را به کیلوگرم تبدیل می‌کنیم. این کار به کمک دانستن چگالی آب و استفاده از ضریب تبدیل مناسب، صورت می‌گیرد.

$$\begin {equation} 2.00 \times 10^{3} \mathrm {g} \mathrm {H}_{2} \mathrm {O}\left (\frac{1 \mathrm { kg}} {1000 \mathrm {g}} \right) =2.00 \mathrm {k g} \mathrm {H } _ {2} \mathrm {O} \end {equation}$$

در نهایت، میزان مولالیته را بر اساس تعریف آن محاسبه می‌کنیم.

$$\begin {equation} \begin {array} {l} \text { molality } =\frac {\text { mol solute }} {\text { kg solvent }} \\ \text { molality }= \frac{35.8 \mathrm {mol} \mathrm {C}_{2} \mathrm {H}_{4} (\mathrm {OH})_{2}} {2 \mathrm {kg} \mathrm {H} _ {2} \mathrm {O}} \\ \text { molality }=17.9 \mathrm{m} \end {array} \end {equation}$$

مثال تبدیل کسر مولی و غلظت مولال

کسر مولی حل‌شونده و حلال ‌را در محلول ۳ مولال سدیم کلرید محاسبه کنید.

در مرحله اول، به کمک تعریف غلظت و کسر مولی، این دو واحد را به یکدیگر تبدیل می‌کنیم. تعریف غلظت مولال برای سدیم کلرید به صورت زیر نوشته می‌شود. همچنین، برای سادگی محاسبات، فرض می‌کنیم که مقدار ۱ کیلوگرم آب داشته باشیم.

$$\frac{3 \ mol Na Cl }{1 Kg \ H _ 2 O }$$

به کمک تعریف غلظت و جرم مولی، تعداد مول آب را محاسبه می‌کنیم:

$$\begin {equation} 1.0 \mathrm {kg} \mathrm {H}_{2} \mathrm {O} \left (\frac {1000 \mathrm{g}}{1 \mathrm{kg}}\right)\left(\frac{\mathrm{mol} \mathrm{H}_{2} \mathrm{O}}{18.02 \mathrm{g}}\right)=55 \mathrm{mol} \mathrm{H}_{2} \mathrm{O} \end {equation}$$

با جایگذاری این مقادیر مولی در تعریف کسر مولی، کسر مولی آب و سدیم کلرید در محلول را محاسبه می‌کنیم.

$$\begin {equation} \begin {aligned} X _{\mathrm {H}_{ 2} \mathrm {O}} &= \frac {\mathrm {mol} \mathrm {H}_{2} \mathrm {O}} {\mathrm {mol} \mathrm {Na Cl} + \mathrm {mol} \mathrm {H} _{2} \mathrm {O}} \\ X_ {\mathrm {H} _ {2} \mathrm {O}} &=\frac {55 \mathrm {mol} \mathrm {H} _{2} \mathrm {O}} {3.0 \mathrm {mol} \mathrm {Na Cl} +55 \mathrm {mol} \mathrm {H}_{2} \mathrm {O}} \\ X_ {\mathrm {H} _{2} \mathrm {O}} & =0.95 \\ X _ {\mathrm {N a C l}} &= \frac {\mathrm {mol} \mathrm {NaCl }} {\mathrm {mol} \mathrm {NaCl } + \mathrm {mol} \mathrm {H}_ {2} \mathrm{O}} \\ X_{\mathrm { NaCl}} &= \frac{3.0 \mathrm {mol} \mathrm {NaCl}} {3.0 \mathrm {mol} \mathrm {NaCl}+55 \mathrm {mol} \mathrm {H}_{2} \mathrm{O}} \\ X_{\mathrm {NaCl}} & =0.052 \end {aligned} \end {equation}$$

معرفی و بررسی خواص کولیگاتیو محلول ها

همانطور که در ابتدای متن ذکر شد، کاهش فشار بخار، افزایش نقطه جوش، نزول نقطه انجماد و فشار اسمزی، از جمله خواص کولیگاتیو محلول‌ها به شمار می‌آیند. در ادامه قصد داریم تا به طور کامل به بررسی خواص کولیگاتیو در محلول‌ها بپردازیم.

فیلم آموزش شیمی عمومی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

نزول فشار بخار

زمانی که تبخیر و میعان با سرعتی برابر انجام شوند، به فشار وارد شده از طرف گاز بر یک مایع، فشار بخار تعادلی می‌گویند. انحلال ماده‌ای غیرفرار در مایعی فرار، کاهش فشار بخار مایع را به همراه خواهد داشت. این پدیده را می‌توان با در نظر گرفتن تاثیر اضافه شدن مولکول‌های حل‌شونده بر فرآیندهای تبخیر و میعان مایع بررسی کرد. برای وقوع تبخیر، مولکول‌های حلال باید در سطح محلول حضور داشته باشند.

حضور مواد حل‌شونده در سطح مایع سبب می‌شوند تا تعداد مولکول‌های کمتری از حلال را در سطح مایع داشته باشیم و این امر، سرعت تبخیر حلال را کاهش می‌دهد. از آن‌جایی که سرعت میعان در فاز گاز با حضور حل‌شونده، تفاوتی نداشته است، نتیجه کلی به این صورت است که تعادل تبخیر-میعان با تعداد مولکول کمتری از حلال در فاز بخار انجام می‌گیرد که یعنی این تعادل، شامل فشار بخار پایین‌تری است.

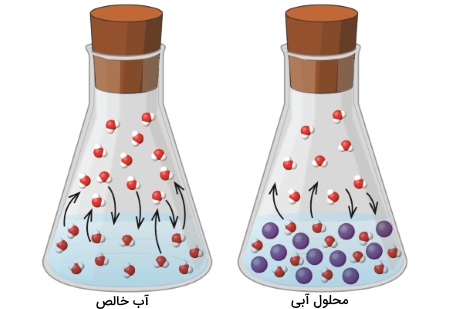
قانون رائول

ارتباط بین فشار بخار اجزای محلول و غلظت آن‌ها را به کمک «قانون رائول»‌ (Raoult's Law) بیان می‌کنند. فشار بخار اعمال شده توسط هر یک از اجزای یک محلول ایده‌آل برابر است با فشار بخار اجزای خالص ضربدر کسر مولی آن‌ها که به صورت زیر تعریف می‌شود:

$$P _ A = X _ A P ^ * _ A$$

• $$P _ A$$: فشار جزئی اعمال شده توسط جزء A در محلول
• $$P ^ * _ A$$: فشار بخار A خالص
• $$X _ A$$: کسر مولی A در محلول

توجه داشته باشید که به هنگام بررسی مخلوط گازها، فشار کل مخلوط، برابر با مجموع فشارهای جزئی تمامی اجزای آن است که آن‌را با نام قانون دالتون می‌شناختیم. فشار بخار کل در محلولی شامل اجزای i برابر با رابطه زیر خواهد بود:

$$\begin {equation} P _ {\text {solution }}= \sum_ {i} P_{ i}= \sum_{ i} X_ {i} P_ {i} ^ { *} \end {equation}$$

در صورتیکه ماده‌ای، فشار بخار بسیار پایین و نزدیک به صفر داشته باشد، به صورت ماده‌ای غیرفرار تعریف می‌شود. در نتیجه، فشار بخار بالای محلولی شامل حل‌شونده غیرفرار، تنها به حلال وابسته است.

$$P _{\text {solution }}=X _{\text {solvent }} P _{\text {solvent }}^{*}$$

مثال محاسبه فشار بخار

فشار بخار محلول ایده‌آلی را حساب کنید که شامل 92/1 گرم گلیسرین با فرمول $$C _ 3 H _ 5 (O H ) _ 3$$ و 184/4 گرم اتانول $$(C _ 2 H _ 5 O H )$$ باشد. فشار بخار اتانول خالص در دمای ۴۰ درجه سانتی‌گراد برابر با 0/178 اتمسفر است. در این دما، گلیسرین ماده‌ای غیرفرار به محسوب می‌شود.

از آن‌جایی که حلال ما در اینجا تنها جزء فرار به شمار می‌آید، فشار بخار آن‌را به کمک قانون رائول و به صورت زیر محاسبه می‌کنند:

$$P _{\text {solution }}=X _{\text {solvent }} P _{\text {solvent }}^{*}$$

در ابتدا به کمک مقادیر جرمی، تعداد مول اجزا را حساب کنید:

$$\begin {equation} \begin {array} {l} 92.1 \mathrm { g C }_{3} \mathrm{ H }_{5}(\mathrm { O H })_ {3} \times \frac {1 \mathrm{ mol} \mathrm {C}_{3} \mathrm {H}_{ 5} (\mathrm {OH})_ {3}} {92.094 \mathrm{g } \mathrm{ C} _ {3} \mathrm {H}_ {5}(\mathrm {O H})_{3}} = 1.00 \mathrm {mol} \mathrm {C}_ {3} \mathrm {H}_{5}(\mathrm {O H}) _{3} \\ 184.4 \mathrm{g} \mathrm {C}_{2} \mathrm {H}_{5} \mathrm {O H} \times \frac{1 \mathrm {mol} \mathrm {C }_{2} \mathrm {H}_{5} \mathrm { O H}} {46.069_ {\mathrm{ g}} \mathrm {C}_{2} \mathrm {H}_{5} \mathrm {O H}}=4.000 \mathrm {mol} \mathrm {C}_{2} \mathrm{H}_{5} \mathrm{O H} \end {array} \end {equation}$$

در ادامه، کسر مولی حلال (اتانول) را محسابه و به کمک قانون رائول، فشار بخار محلول را محاسبه می‌کنیم.

$$\begin {equation} \begin {array} {l} X _ {\mathrm{ C}_{2} \mathrm {H}_{5} \mathrm {O H}} = \frac {4.000 \mathrm { mol}} {(1.00 \mathrm {mol}+4.000 \mathrm {mol})} = 0.800 \\ P_ { \mathrm{solv}}= X _ {\mathrm {solv}} P_ {\mathrm {solv}}^{*}=0.800 \times 0.178 \mathrm {atm}=0.142 \mathrm{atm} \end {array}\end {equation}$$

افزایش نقطه جوش

در مبحث نقطه جوش به یاد دارید که نقطه جوش نرمال یک ماده به دمایی می‌گفتند که در آن، فشار بخار برابر با 1 اتمسفر باشد. اگر یک حل‌شونده غیرفرار، فشار بخار محلولی را کاهش دهد، باید بر نقطه جوش آن نیز تاثیرگذار باشد. از آن‌جایی که فشار بخار یک محلول در دمایی مشخص، کمتر از فشار بخار حلال خالص آن است، برای رسیدن به فشار بخار ۱ اتمسفر، به دمای بیشتری از نقطه جوش نرمال حلال نیاز داریم. بنابراین، نقطه جوش یک محلول، همواره بیش‌تر از حلال خالص آن است.

برای بررسی صحت این پدیده می‌توانیم دیاگرام فازی یک محلول آبی را با آب خالص مقایسه کنیم. فشار بخار محلول در همه دماها، کمتر از نوع خالص آن است. در نتیجه، نمودار بخار-مایع در محلول، خط افقیِ متناظر با فشار ۱ اتمسفر را در دمای بیش‌تری نسبت به آب خالص قطع می‌کند.

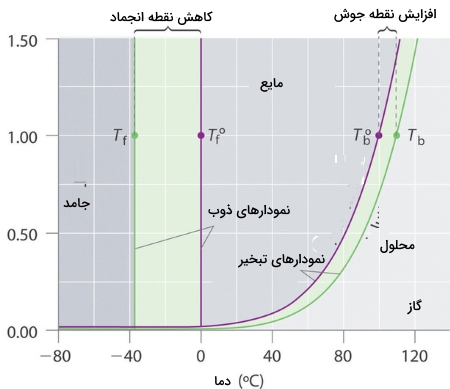
مقدار افزایش نقطه جوش، به مقدار کاهش فشار بخار بستگی دارد. همانطور که پیش‌تر ذکر کردیم، کاهش فشار بخار، با غلظت حل‌شونده در محلول متناسب است. بنابراین، مقدار افزایش نقطه جوش باید با غلظت حل‌شونده متناسب باشد.

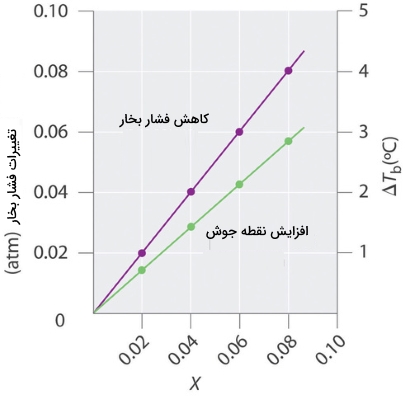
مقدار افزایش نقطه جوش $$(\Delta b )$$ را به صورت اختلاف بین نقطه جوش حل‌شونده و حلال خالص ذکر می‌کنند. در این رابطه،‌ $$T_ b$$ نقطه جوش محلول و $$T ^0 _b$$ نقطه جوش حلال خالص است.

$$Δ T _ b= T_ b − T ^0 _b$$

به کمک رابطه زیر، غلظت (مولالیته) را با میزان افزایش نقطه جوش $$(\Delta b )$$ مرتبط می‌کنیم.

$$Δ T _ b = m K _ b$$

• $$m$$:  غلظت مولال
• $$K_b$$: ثابت مولال افزایش نقطه جوش با واحد $$^ \circ C / m$$

برای محلول‌های نسبتا رقیق، مقدار هر دو خاصیت بالا با غلظت حل‌شونده متناسب است. در جدول زیر، ثابت‌های افزایش نقطه جوش و نزول نقطه انجماد را برای بسیاری از محلول‌های مورد استفاده در آزمایشگاه‌های شیمی نشان میدهد.

مثال برای محاسبه نقطه جوش یک محلول

با فرض این‌که محلولی ایده‌آل داشته باشیم، نقطه جوش یک محلول 0/33 مولال بنزن شامل حل‌شونده غیرفرار را محاسبه کنید.

این سوال را می‌توان در دو مرحله حل کرد. در مرحله اول و با داشتن مولالیته محلول، تغییر نقطه جوش را محاسبه می‌کنیم و در مرحله بعد، نقطه جوش جدید محاسبه خواهد شد.

مرحله اول: تغییرات نقطه جوش را محاسبه می‌کنیم.

$$\begin {equation} \Delta T _{\mathrm {b}}= K _ {\mathrm {b}} m=2.53^ {\circ} \mathrm {C} m ^ {-1} \times 0.33 m = 0.83^ {\circ} \mathrm {C} \end {equation}$$

مقدار افزایش نقطه جوش را به نقطه جوش حلال خالص اضافه و نقطه جوش جدید را محاسبه کنید.

نقطه جوش جدید: $$80.1+0.83 = 80.9\ ^ \circ C$$

نزول نقطه انجماد

دیاگرام فازی که در تصویر قبل دیدیم، نشان می‌دهد که انحلال حل‌شونده‌ای غیرفرار در آب، نه تنها موجب افزایش نقطه جوش می‌شود، بلکه نزول نقطه انجماد را نیز به همراه دارد. نمودار جامد-مایع محلول، خط متناظر با فشار ۱ اتمسفر را در دمایی کمتر از نمودار مربوط به آب خالص، قطع می‌کند.

فیلم آموزش شیمی فیزیک ۲ – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

برای درک این مفهوم، فرض می‌کنیم نمونه‌ای آب در دمای انجماد نرمال داریم که بین مایع و جامد، تعادلی دینامیک (پویا) برقرار شده است به این معنی که مولکول‌های آب به طور پیوسته با سطح یخ برخورد می‌کنند و وارد فاز جامد می‌شوند و با همان سرعت نیز مولکول‌های آب، سطح یخ را ترک می‌کنند و به فاز مایع وارد می‌شوند. اگر حل‌شونده‌ای غیرفرار همچون گلوکز را در مایع حل کنیم، مولکول‌های حل‌شده گلوکز، تعداد برخوردها به ازای واحد زمان بین مولکول‌های آب و سطح یخ را کاهش می‌دهند زیرا برخی از مولکول‌های برخورد کننده با یخ، از نوع مولکول‌های گلوکز هستند.

مولکول‌های گلوکز، ساختار بسیار متفاوتی نسبت به آب دارند و در داخل شبکه بلور یخ جای نمی‌گیرند. در نتیجه، حضور مولکول‌های گلوکز در محلول، تنها سبب کاهش سرعت برخورد مولکول‌های آب به سطح یخ و انجماد آن‌ها می‌شوند. در این میان، سرعت خروج مولکول‌های آب از سطح یخ و ورود به فاز مایع، بدون تغییر باقی می‌ماند. این اثر در نهایت سبب ذوب یخ خواهد شد. تنها راه برای برقراری مجدد تعادل پویا بین جامد و مایع،‌ کم کردن دمای سیستم است که سرعت خروج مولکول‌های آب از سطح یخ را کاهش می‌دهد. این کار تا زمان برابری سرعت خروج مولکول‌ها از یخ و برخورد مولکول‌های آب به سطح یخ ادامه پیدا می‌کند.

همانند روشی که در افزایش نقطه جوش مطرح کردیم، نزول نقطه انجماد $$(\Delta T _ f)$$ به عنوان اختلاف بین نقطه انجماد حلال خالص و نقطه انجماد محلول بیان می‌شود که در آن، $$T^0_ f$$، نقطه انجماد حلال خالص و $$T _ f$$ نقطه انجماد محلول است.

$$ΔT _ f= T^0_ f− T _f$$

همانطور که در رابطه بالا مشاهده می‌کنید، ترتیب عبارات نسبت به رابطه افزایش نقطه جوش تغییر کرده‌اند تا میزان نزول نقطه انجماد، عدد مثبتی باشد. رابطه بین $$ΔT _ f$$ و غلظت حل‌شونده، با رابطه‌ زیر بیان می‌شود که در آن، $$m$$ مولالیته محلول و $$K _ f$$، ثابت مولال نزول نقطه انجماد محلول با واحد $$^ \circ C / m$$ است.

$$Δ T _ f = m K _ f$$

همانند $$K _b$$، هر محلول، مقدار مشخصی برای $$K_f$$ دارد که در جدول بالا نمایش داده شده است. خواص کولیگاتیو افزایش نقطه جوش و نزول نقطه انجماد، هر دو به تعداد ذرات غیرفرار حل‌شونده بستگی دارند. افرادی که در مناطق سردسیر زندگی می‌کنند از خواص کولیگاتیو بویژه در نزول نقطه انجماد، استفاده می‌کنند. به طور مثال، از نمک برای ذوب شدن یخ و برف در جاده‌ها کمک می‌گیرند و همچنین با اضافه کردن اتیلن گلایکول به سیستم خنک‌کننده موتور خودرو، از یخ زدن آن در زمان سرما جلوگیری می‌کنند. علاوه بر این، در برخی موارد، به مایع شیشه‌شوی خودرو، مقداری متانول برای جلوگیری از یخ‌زدگی اضافه می‌شود.

مثال نمک پاشی جاده‌

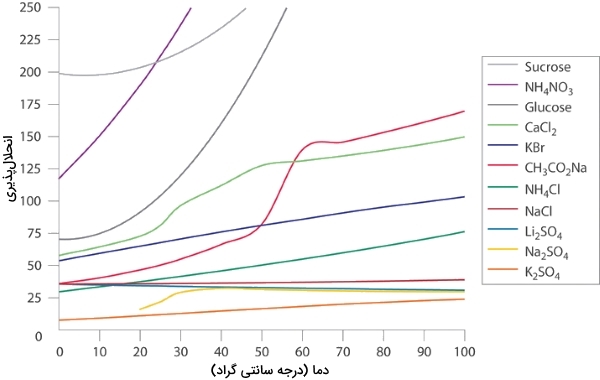
در مناطق سردسیر، با پاشیدن نمک‌های $$NaCl$$ و $$CaCl_2$$ بر روی جاده‌ها، از یخ‌زدن آن‌ها جلوگیری می‌کنند تا ایمنی رانندگان و جاده افزایش پیدا کند. از داده‌های نمودار زیر کمک بگیرید تا غلظت دو محلول اشباع $$NaCl$$ و $$CaCl_2$$ را تخمین بزنید و نقطه انجماد هر دو محلول را محاسبه کنید. در نهایت، با محاسبه نقطه انجماد، بررسی کنید که کدام‌یک از نمک‌ها در جلوگیری از یخ‌زدگی تاثیر بیش‌تری دارند.

نمودار زیر، انحلال‌پذیری جامدهای آلی و معدنی در آب به عنوان تابعی از دما نشان داده شده است. همانطور که مشاهده می‌کنید، این انحلال‌پذیری با افزایش دما، افزایش یا کاهش پیدا می‌کند و شدت آن در ترکیبات مختلف با یکدیگر متفاوت است.

برای حل این سوال، دو مرحله زیر را دنبال کنید:

• انحلال‌پذیری هر نمک را در 100 گرم آب و به کمک نمودار بالا تخمین بزنید.
• غلظت نمک‌های حل‌شده را در محلول تعیین کنید و مقادیر بدست آمده را در رابطه مربوط به نزول نقطه انجماد جایگذاری کنید.

با توجه به نمودار بالا، انحلال‌پذیری $$NaCl$$ و $$CaCl_2$$ به ترتیب در حدود 36 و ۶۰ گرم در دمای صفر درجه سانتی‌گراد خواهد بود. غلظت‌های متناظر با این جرم‌ها نیز به صورت زیر محاسبه می‌شوند:

$$\require {cancel} m_ {Na Cl }=\left ( \dfrac{36 \; \cancel{g \;N a Cl}} {100 \;\cancel {g} \;H _ 2 O} \right) \left (\dfrac {1\; mol\; Na Cl} {58.44\; \cancel { g\; NaCl} } \right) \left ( \dfrac {1000\; \cancel {g}} {1\; k g } \right) = 6.2\; m<br /> $$

$$m _ {Ca Cl_2}= \left (\dfrac {60\; \cancel {g\; C a Cl _2}}{100\;\cancel {g}\; H_ 2O} \right) \left (\dfrac {1\; mol\; C a C l _ 2} {110.98\; \cancel {g\; C a C l _ 2}} \right) \left (\dfrac {1000 \;\cancel {g} } {1 kg} \right ) = 5.4\; m \nonumber$$

جرم فرمولی (جرم مولی) کمتر $$NaCl$$ سبب شده است تا محلول اشباع آن، غلظت بیش‌تری نسبت به $$CaCl_2$$ داشته باشد. البته با توجه به این‌که این ترکیبات، یونی هستند و در آب تفکیک می‌شوند، با تفکیک $$NaCl$$ و $$CaCl_2$$ در آب، به ترتیب به ازای هر واحد فرمولی، ۲ و ۳ یون خواهیم داشت و غلظت حقیقی ذرات حل‌شده در آب به صورت $$2 × 6.2 m = 12 m$$ برای $$NaCl$$ و $$3 × 5.4 m = 16 m$$ برای $$CaCl_2$$ محاسبه می‌شود. با توجه به اطلاعات بدست آمده، میزان نزول نقطه انجماد در هر دو نمک قابل محاسبه خواهد بود:

$$Na C l: ΔT _ f =m K_ f= (12\; \cancel {m} )(1.86°C/ \cancel {m})=22°C$$

$$C a C l 2: ΔT _ f = m K _ f = (16\;\cancel { m } )(1.86°C/ \cancel { m } ) = 30°C \nonumber$$

با توجه به این‌که نقطه انجماد آب برابر با صفر درجه سانتی‌گراد است، نقطه انجماد محلول‌های حاصل از انحلال $$NaCl$$ و $$CaCl_2$$ به ترتیب برابر با $$-22\ ^ \circ C$$ و $$-30\ ^ \circ C$$ است. توجه داشته باشید که $$CaCl_2$$ در نزول نقطه انجماد، تاثیر بیش‌تری دارد  چراکه محلول آن به ازای هر واحد فرمولی، شامل ۳ یون است.

با توجه به اینکه انحلال‌پذیری هر دو نمک با کاهش دما، کم می‌شود، برای نزول نقطه انجماد، مقدار مشخصی از نمک را می‌توان استفاده کرد. همچنین، اگر دما پایین‌تر از حداکثر توانایی نمک برای کاهش دما باشد، بهره‌گیری از این نمک‌ها، تاثیری در یخ‌زدن جاده‌ها و سطوح نخواهد داشت.

تعیین جرم مولی به کمک خواص کولیگاتیو

از خواص کولیگاتیو محلول‌ها می‌توان برای تعیین جرم مولی ترکیبات ناشناخته استفاده کرد. یکی از روش‌های آزمایشگاهی با حداقل تجهیزات، اندازه‌گیری نقطه انجماد یک محلول با جرم مشخصی از حل‌شونده است. این روش در محلول‌های رقیق (کمتر از ۱ درصد جرمی) به طور دقیقی قابل انجام است زیرا تغییرات در نقطه انجماد، به اندازه‌ای زیاد هستند که بتوان به طور دقیق آن‌ها را اندازه‌گیری کرد.

فیلم آموزش شیمی عمومی ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

با مقایسه مقادیر $$K_f$$ و $$K_b$$ در جدول بالا، در می‌یابیم که برای یک محلول مشخص، تغییرات نقطه جوش، کمتر از تغییرات نقطه انجماد است. بنابراین، اندازه‌گیری میزان افزایش نقطه جوش، دشوارتر خواهد بود. به همین دلیل، برای تعیین جرم مولی، به طور معمول از میزان نزول نقطه انجماد بهره‌ می‌گیرند. با نگاهی به جدول بالا در می‌یابیم که کافور، میزان $$K _ f$$ بالایی دارد و به همین دلیل، به طور معمول برای تعیین جرم مولی ترکیبات آلی از آن استفاده می‌شود.

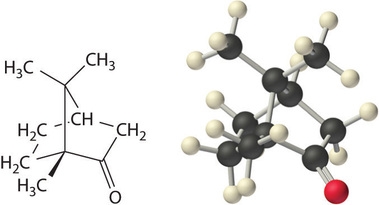
مثال تعیین جرم مولی گوگرد از طریق خواص کولیگاتیو

میزان 7/08 گرم از گوگرد عنصری را در 75 گرم از $$CS_ 2$$ بمنظور تهیه محلولی با نقطه انجماد $$-113.5\ ^ \circ C$$ حل کرده‌ایم. از مقادیر داده شده برای محاسبه جرم مولی گوگرد عنصری (مولکول شامل گوگرد) و پیدا کردن فرمول مولکول‌های حل شده گوگرد استفاده کنید.

برای حل این سوال، ۳ مرحله زیر را دنبال می‌کنیم:

• از رابطه مربوط به محاسبه $$\Delta T _ f$$، نقطه انجماد محلول و نقطه انجماد $$CS_2$$ در جدول استفاده و میزان نزول نقطه انجماد را محاسبه می‌کنیم.
• به کمک مولالیته محاسبه شده، تعداد مول‌های حل‌شونده تعیین خواهد شد.
• به کمک جرم و تعداد مول‌های حل‌شونده،‌ جرم مولی گوگرد در محلول را محاسبه می‌کنیم. نتایج را بر جرم مولی اتم گوگرد تقسیم می‌کنیم تا عدد مربوط به فرمول مولکول‌های حل‌شده گوگرد محاسبه شود.

در مرحله اول، میزان نزول نقطه انجماد را محاسبه می‌کنیم:

$$Δ T _ f = T ^ 0 _f − T_ f = −112.1°C − (−113.5°C)=1.4°C \nonumber$$

با جایگذاری در رابطه مربوط به نزول نقطه انجماد، مولالیته محلول، محاسبه خواهد شد:

$$m = \dfrac { Δ T _f } {K _f}= \dfrac{1.4° \cancel {C}} {3.74° \cancel {C} / m } =0.37\;m \nonumber$$

تعداد کل مول‌های حل‌شونده در محلول را از رابطه زیر محاسبه می‌کنیم:

$$= \left (\dfrac {0.37 mol} {\cancel {k g} }\right) (75.0\; g) \left (\dfrac {1 kg} {1000\; g} \right) =0.028 \;mol \nonumber$$ تعداد مول حل‌شونده

حال می‌دانیم که ۷/08 گرم از گوگرد عنصری، متناظر با 0/028 مول حل‌شونده است. بنابراین، جرم مولی گوگرد حل‌شده برابر است با:

$$=\dfrac{7.08\; g}{0.028\; mol}=260\; g/mol \nonumber$$ جرم مولی

جرم مولی اتم گوگرد برابر با $$32 g/ mol$$ است. بنابراین،‌ در هر مول باید به میزان $$260/32 = 8.1$$ اتم گوگرد داشته باشیم و این عدد، متناظر با فرمول $$S_8$$ است.

فشار اسمزی

فشار اسمزی از جمله خواص کولیگاتیو محلول‌ها به شمار می‌آید که به هنگام استفاده از غشای نیمه‌تراوا مشاهده می‌شود. این غشا، به صورت مانعی عمل می‌کند که حفرات آن به اندازه‌ای کوچک هستد که مولکول‌های حلال از آن عبور کنند اما مولکول‌ها یا یون‌های حل‌شونده توانایی عبور نداشته باشند. در این شرایط، به جریان خالص عبوری حلال از میان غشای نیمه‌تراوا، «اسمز» (Osmisis) می‌گویند. جهت جریان هموراه از طرف محلول با غلظت کم از حل‌شونده به طرف محلول با غلظت بیش‌تر است.

پدیده اسمز را می‌توان به کمک لوله‌ای U شکل همچون تصویر زیر نشان داد. در سمت چپ این لوله، آب خالص و در سمت راست، محلول رقیقی از گلوکز وجود دارد. جریان خالص آب از میان غشا تا زمانی ادامه می‌یابد که تغییر سطح مایع در دو طرف لوله ثابت شود که به معنی برقراری تعادل خواهد بود. فشار اسمزی $$(\Pi)$$ محلول گلوکز به اختلاف فشار بین دو طرف لوله می‌گویند که در این‌جا، این تفاوت به کمک اختلاف ارتفاع مایع بیان می‌شود.

با این وجود، غشای تراوا سبب می‌شود مولکول‌های آب بتوانند در هر دو طرف لوله حرکت داشته باشند. سرعت جریان در دو طرف یکسان نیست زیرا غلظت آب در دو طرف با یکدیگر برابر نیست. این جریان آب را می‌توان با اعمال فشار در سمت راست لوله متوفق کرد که این فشار اعمال شده برابر با فشار اسمزی محلول گلوکز خواهد بود.

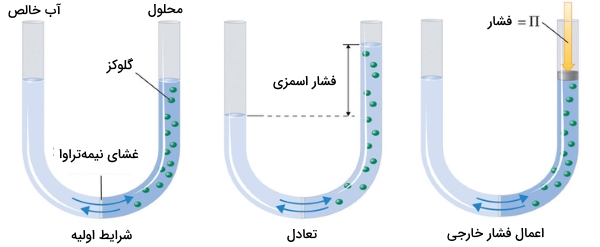
در تصویر بالا، محلولی رقیق از گلوکز در آب نشان داده شده است. سمت چپ این لوله با ارتفاعی یکسان از آب خالص پر شده است. این دو قسمت در لوله توسط یک غشای نیمه‌تراوا از یکدیگر جدا شده‌اند. از آن‌جایی که جریان حلال خالص از چپ به راست، بیش‌تر از جریان در جهت روبرو است، سطح مایع در سمت راست لوله افزایش پیدا می‌کند. در حالت دوم و زمانیکه تعادل برقرار باشد، اختلاف فشار، برابر با فشار اسمزی خواهد بود و سرعت جریان در هر دو طرف لوله یکسان می‌شود. اگر فشاری معادل با فشار اسمزی، در سمت راست لوله اعمال کنیم، شرایط به حالت اولیه می‌رسد.

همانند سایر خواص کولیگاتیو محلول‌ها، فشار اسمزی یک محلول به غلظت ذرات حل‌شونده بستگی دارد. فشار اسمزی از قانونی شبیه به رابطه گازهای ایده‌آل پیروی می‌کند.

$$\Pi = \dfrac { n R T } {V} = M R T$$

• $$M$$: مولاریته محلول
• $$R$$: ثابت جهانی گازها (ثابت گازهای ایده‌آل)
• $$T$$: دمای مطلق

فشار اسمزی در مثال زیر مورد بررسی قرار می‌گیرد و در این مثال می‌بینیم که برای محلول‌های رقیق نیز فشار اسمزی، فشار بالایی خواهد بود.

مثال محاسبه فشار اسمزی

زمانی که نوع خاصی از مخمر را در محلولی غلیظ از نمک قرار دهیم، این مخمرها با تولید غلظت‌هایی از گلیسرول، با فشار اسمزی محیط اطراف مقابله می‌کنند. فرض کنید سلول‌های مخمر در محلول آبی شامل 4 درصد جرمی $$NaCl$$ قرار داده شده است. چگالی محلول در دمای 25 درجه سانتی‌گراد برابر با $$1.02 g/mL$$ است. فشار اسمزی محلول $$NaCl$$ را محاسبه کنید.

اگر فشار اسمزی داخل سلول مخمر، برابر با 7/3 اتمسفر و متناظر با غلظت 0/3 مولار باشد، چه میزان غلظت را باید سلول‌های مخمر سنتز کنند تا به طور دقیق با فشار اسمزی خارجی در دمای ۲۵ درجه سانتی‌گراد برابر شود.

برای حل این سوال مراحل زیر را دنبال کنید:

• مولاریته محلول $$NaCl$$ را به کمک جرم فرمولی حل‌شونده و چگالی محلول محاسبه کنید. در نهایت، غلظت کلی ذرات حل‌شده را بدست آورید.
• از رابطه فشار اسمزی برای محاسبه فشار اسمزی محلول استفاده کنید.
• فشار اسمزی نرمال سلول را از فشار اسمزی محلول نمکی کم کنید تا فشار اضافی مورد نیاز برای ایجاد موازنه بین فشارها بدست بیاید. سپس به کمک رابطه فشار اسمزی، مولاریته گلیسرول مورد نیاز را حساب کنید.

حل

در هر 100 گرم از محلول مورد نظر، ۴ گرم $$NaCl$$ داریم. با استفاده از جرم مولی (جرم فرمولی) نمک $$(58.44 g/mol)$$ و چگالی محلول، مولاریته را محاسبه می‌کنیم.

$$\begin {align*} M_ {N a C l} &= \dfrac {moles\; N a C l }{\text{liter solution}} \\[4pt] &=\left (\dfrac{4.0 \; \cancel { g } \; N a C l} {58.44\; \cancel {g}/ mol\; N a C l } \right) \left (\dfrac {1}{100\; \cancel {g \;solution} } \right) \left ( \dfrac{1.02\; \cancel {g \; solution}} {1.00\; \cancel { m L }\; solution} \right ) \left( \dfrac {1000\; \cancel {m L} } {1\; L } \right) \\[4pt] &= 0.70\; M\; {N a C l} \end {align*}$$

با توجه به این‌که ۱ مول $$NaCl$$ در اثر انحلال، ۲ مول ذره تولید می‌کند، غلظت کلی ذرات حل‌شده در محلول برابر با $$(2)(0.70 M) = 1.4 M$$ خواهد بود. حال به کمک روابط داده شده می‌توانیم فشار اسمزی محلول را محاسبه کنیم.

$$\begin {align*} \Pi &= M R T \\[4pt] &=(1.4 \; mol / L) \left[ 0.0821\; ( L⋅atm) /(K⋅ m o l) \right ] (298\; K)\\[4pt] &=34 \;atm \end {align*}$$

برای موازنه دقیق بین فشار اسمزی محیط و فشار اسمزی مخمرها، این مخمرها باید میزان $$(34 atm − 7.3 atm) = 27 atm$$ فشار را تولید کنند. با توجه به این‌که گلیسرول یک الکترولیت نیست،‌ با استفاده از رابطه بالا می‌توانیم مولاریته متناظر با فشار اسمزی را محاسبه کنیم.

$$\begin {align*} M&= \dfrac {\Pi } {R T } \\[4pt] &= \dfrac{27\; \cancel {atm}} {[0.0821(L⋅\cancel{atm})/(\cancel{K}⋅mol)] (298 \;\cancel{K})}\\[4pt] &=1.1 \;M \;\text{glycerol} \end{align*}$$

با حل این سوال متوجه می‌شویم که تنها راهی که فشار اسمزی داخل سلول با فشار اسمزی محلول، یکی باشد این است که غلظت‌های ذرات حل شده با یکدیگر برابر باشند. غلظت ذرات حل شده در سلول برابر با 0/3 مولار بود و غلظت ذرات $$NaCl$$ را برابر با 1/4 مولار محاسبه کردیم. بنابراین، سلول‌های مخمر باید به میزان کافی گلیسرول تولید کنند تا غلظت داخلی ذرات حل‌ شده را از 0/3 مولار به 1/4 مولار برسانند که این میزان، دقیقا با عدد محاسبه شده برابری می‌کند.

فشار اسمزی در طبیعت

با توجه به مقدار بالای فشار اسمزی، این پدیده در بیوشیمی، زیست‌شناسی و پزشکی،‌ کاربرد بسیاری دارد. تقریبا تمامی موانعی که به نوعی یک موجود زنده یا سلولی را از محیط اطراف جدا کند، همچون یک غشای نیمه‌تراوا عمل می‌کنند که در این حالت، آب اجازه عبور دارد اما ذرات حل‌شده نمی‌توانند از آن عبور کنند. همین امر نیز در مورد اجزای داخلی یک سلول یا ارگانیسم صدق می‌کند. برخی از اجزای بدن همچون کلیه‌ها، به طور نسبی دارای غشای نیمه‌تراوا هستند که به کمک فرآیند دیالیز، از عبور درشت‌مولکول‌هایی همچون پروتئین‌ها جلوگیری می‌کنند.

از همین اصل برای حفظ میوه‌ها و ویتامین‌های ضروری آن‌ها در طول زمستان استفاده می‌شود. در حقیقت، غلظت بالای شکر در مربا و ژله، علاوه بر شیرین کردن طعم میوه‌ها، به میزان بسیار زیادی فشار اسمزی را نیز افزایش می‌دهند. در نتیجه، با این روش، از رشد باکتری‌های بجا مانده در فرآیند پخت، جلوگیری می‌شود. به طور مشابه، با اضافه کردن نمک (نمک‌سود کردن) گوشت‌ها، می‌توان مدت بیش‌تری آن‌ها را نگهداری کرد.

لازم به ذکر است علاوه بر مویینگی، درختان برای انتقال آب و سایر مواد مغذی، از فشار اسمزی بهره می‌گیرند. تبخیر آب از برگ درختان، غلظت نمک را در آن محل افزایش می‌دهد و این کار سبب ایجاد فشار اسمزی می‌شود که آب را از ریشه‌ها به برگ‌ها برساند.

خواص کولیگاتیو و تصفیه آب به کمک اسمز معکوس

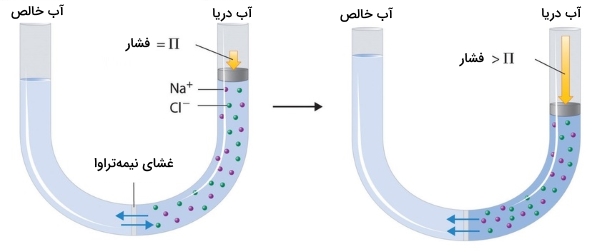
به کمک خواص کولیگاتیو و روشی به نام «اسمز معکوس» (Reverse Osmosis)، از آب دریا می‌توان آب خالص تهیه کرد. همانطور که در تصویر زیر نشان داده شده است، اعمال فشار زیاد به آب دریا (آب شور) سبب جریان یافتن مولکول‌های آب و عبور آن‌ها از غشای نیمه‌‌تراوا و استخراج آب خالص می‌شود. در مناطق صحرایی از این تاسیسات بمنظور تصفیه آب‌ها در حجم عظیم بهره می‌گیرند. دستگاه‌های کوچک تصفیه آب نیز می‌توانند در هر ساعت، حدود پنج لیتر آب شیرین تولید کنند.

خواص کولیگاتیو محلول‌های الکترولیت

تا اینجای آموزش فرض کردیم که در محلول‌های الکترولیت، برای بدست آوردن غلظت ذرات حل شده می‌توانیم غلظت مولی آن‌ها را در تعداد یون‌ها به ازای واحد فرمولی ضرب کنیم. با این کار، غلظت حقیقی ذرات حل شده در یک محلول الکترولیت محاسبه می‌شود. از این مدل (روش) ساده استفاده کردیم تا خواصی همچون نقطه انجماد، نقطه ذوب، فشار بخار و فشار اسمزی را محاسبه کنیم.

فیلم آموزش شیمی فیزیک – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

اگر این روش (مدل) کاملا درست بود، انتظار داشتیم میزان نزول نقطه انجماد محلول 0/1 مولار سدیم کلرید، به طور دقیق ۲ برابر محلول 0/1 مولار گلوکوز باشد. اما در واقعیت، این شرایط همواره برقرار نیست. در مقابل، تغییرات مشاهده شده در نقطه انجماد محلول 0/1 مولار $$NaCl$$ و $$KCl$$، به طور مشخصی کمتر از مقدار مورد انتظار است. این امر نشان می‌دهد، ذرات کمتری از آن‌چه که انتظار داشتیم در محلول حضور دارند.

رابطه بین تعداد حقیقی مول‌های حل‌شونده نسبت به تعداد ظاهری آن‌ها بر اساس خواص کولیگاتیو، به «ضریب وانت هوف» (Van't Hoff Factor) موسوم است که با $$i$$ نشان می‌دهند.

تعداد مول حل‌شونده در محلول / تعداد ظاهری ذرات در محلول = i

در نتیجه، ضریب وانت هوف معیاری برای اندازه‌گیری میزان انحراف از رفتار ایده‌آل به شمار می‌آید. هرقدر میزان ضریب وانت‌هوف پایین‌تر باشد، انحراف بیش‌تری خواهیم داشت. داده‌های جداول نشان می‌دهند که ضریب وانت هوف برای ترکیبات یونی، مقداری کمتر از مورد انتظار دارند و این بدان معنی است که محلول‌های آن‌ها تعداد ذرات حل‌شده کمتری نسبت به میزان پیش‌بینی شده در واحد فرمولی دارند. با افزایش غلظت محلول‌ها، ضریب وانت‌هوف کاهش می‌یابد زیرا ترکیبات یونی به طور کامل در محلول‌های آبی تفکیک نمی‌شوند.

جمع‌بندی

در این مطلب به طور کامل به بررسی خواص کولیگاتیو در محلول‌ها پرداختیم. دیدیم که خواص کولیگاتیو یک محلول، تنها به تعداد کل ذرات حل‌شده در محلول بستگی دارد و ارتباطی به ماهیت شیمیایی آن‌ها ندارد. خواص کولیگاتیو شامل فشار بخار، نقطه جوش، نقطه انجماد و فشار اسمزی بودند که تغییرات هر یک را بررسی کردیم.

تغییرات در هر یک از خواص کولیگاتیو به این شکل بود که با اضافه کردن حل‌شونده‌ای غیر فرار، فشار بخار محلول، کاهش پیدا می‌کرد. فشار بخار یک محلول با کسر مولی حلال در محلول متناسب است و این تناسب را با قانون رائول بیان کردیم. محلول‌هایی که از قانون رائول پیروی می‌کنند، موسوم به محلول‌های ایده‌آل هستند.

افزایش نقطه جوش $$(\Delta T _ b)$$ و نزول نقطه انجماد $$(\Delta T _ f)$$ از دیگر خواص کولیگاتیو محلول‌ها بودند که به ترتیب، به صورت اختلاف نقطه جوش و نقطه انجماد محلول با حلال خالص تعریف می‌شوند. این خواص کولیگاتیو با مولالیته محلول متناسب هستند.

در انتهای مطلب نیز در خصوص نوع دیگری از خواص کولیگاتیو یعنی فشار اسمزی صحبت کردیم. زمانی که یک محلول و حلال خالص به کمک غشایی نیمه‌تراوا از یکدیگر جدا شوند، این غشا سبب می‌شود مولکول‌های حلال از میان آن عبور کنند اما مولکول‌های حل‌شونده توانایی عبور نداشته باشند. همین امر سبب ایجاد فشاری موسوم به فشار اسمزی خواهد شد که برابر با اختلاف فشار بین دو طرف لوله U‌شکل بود.

همچنین، در بررسی خواص کولیگاتیو محلول‌ها و پس از معرفی فشار اسمزی، به پدیده اسمز پرداختیم. به جریان خالص عبوری حلال از میان غشای نیمه‌تراوا به دلیل تفاوت غلظت حل‌شونده در دو طرف، اسمز می‌گویند. دیدیم که فرآیند دیالیز از غشای نیمه‌تراوا برای عبور دادن مولکول‌های کوچک استفاده می‌‌کند.

در محلول‌های غلیظ‌تر یا محلول‌هایی نمکی همراه با یون‌هایی به شدت باردار،‌ کاتیون‌ها و آنیون‌ها سبب تشکیل جفت‌های یونی خواهند شد که این امر، تاثیر آن‌ها بر خواص کولیگاتیو محلول را کاهش می‌دهد. تشکیل این جفت‌های یونی توسط ضریب وانت‌هوف تعریف شد که برابر با نسبت تعداد ظاهری ذرات موجود در محلول به تعداد پیش‌بینی شده از طریق استوکیومتری نمک بود.