تابع وایرشتراس — به زبان ساده

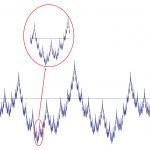
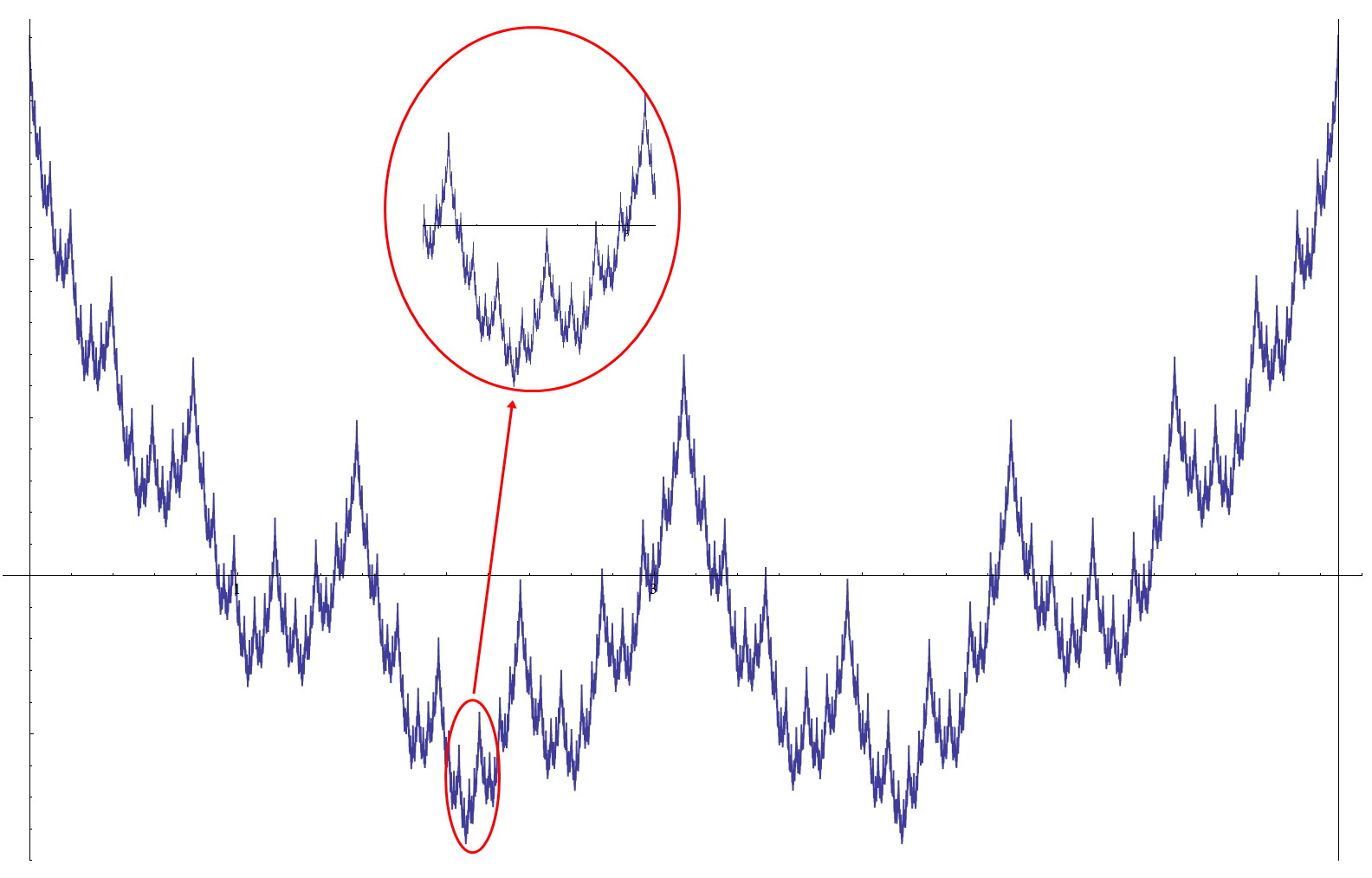
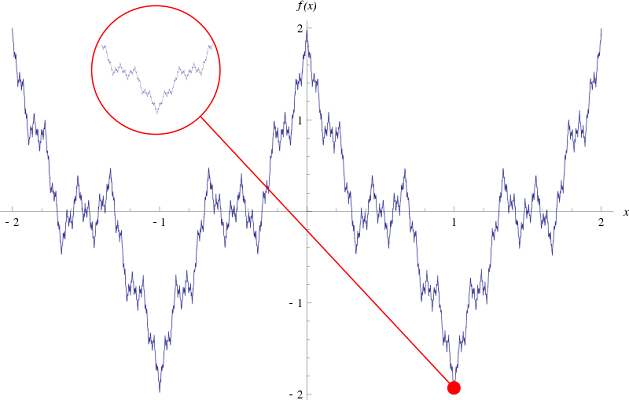
در ریاضیات، «تابع وایرشتراس» (Weierstrass Function) مثالی از یک تابع حقیقی است که علی‌رغم اینکه همه‌ جا پیوسته است، اما در هیچ جایی مشتق‌پذیر نیست. این تابع را «کارل وایرشتراس» (Karl Weierstrass)، ریاضی‌دان آلمانی، کشف کرد.

تابع وایرشتراس

توابع سینوس و کسینوس را معمولاً به صورت هندسی توصیف می‌کنیم و آن‌ها را به کل $$\mathbb{R}$$ تعمیم می‌دهیم. فرض می‌کنیم گزاره‌های زیر را برای این توابع داشته باشیم:

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

(الف) سینوس و کسینوس روی $$\mathbb{R}$$ پیوسته هستند.

(ب) برای هر برای هر $$x \in \mathbb { R}$$، داریم: $$| \sin ( x) | , | \cos ( x) | \le 1$$.

(ج) برای هر $$x \in \mathbb { R}$$ به جز $$0$$، داریم: $$\left | \frac {\sin (x)} { x } \right | \le 1$$.

(د) برای هر $$x , y \in \mathbb { R}$$، داریم: $$\cos ( x ) - \cos ( y ) = - 2 \sin \left ( \frac { x + y }{ 2 } \right ) \sin \left ( \frac { x - y } { 2 } \right )$$.

(ه) برای هر $$x , y \in \mathbb { R}$$، داریم: $$\cos ( x + y ) = \cos ( x ) \cos ( y ) - \sin ( x ) \sin ( y )$$.

این موارد را می‌توان برای مثال با استفاده از نمایش سری توانی به دست آورد:

$$\large \sin ( x ) = \sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } } { ( 2 n + 1 ) ! } x ^ { 2 n + 1 }$$   و  $$\large \cos ( x ) = \sum _ { n = 0 } ^ { \infty } \frac { ( - 1) ^ { n } } { ( 2 n ) ! } x ^ { 2 n }$$

قضیه: فرض کنید $$a \in ( 0 , 1 )$$ و $$b$$ یک عدد صحیح فرد باشد به گونه‌ای که $$a b > 1 + \frac {3 \pi } { 2 }$$. در نتیجه، سریِ

$$\large f ( x ) = \sum _ { n = 0 } ^ \infty a ^ n \cos ( b ^ n \pi x )$$

به صورت یکنواخت روی $$\mathbb { R}$$ همگرا می‌شود و یک تابع پیوسته، اما مشتق‌ناپذیر در همه جا را تعریف می‌کند.

تابع قضیه بالا «تابع وایرشتراس» نامیده می‌شود. قبل از اثبات قضیه بالا، لم زیر را بیان می‌کنیم.

لم (آزمون M وایرشتراس): فرض کنید $$( E , d )$$ یک فضای متریک باشد و برای هر $$n \in \mathbb{ N}$$، تابع $$f _ n : E \to \mathbb { R}$$ را داشته باشیم. فرض کنید برای هر $$n \in \mathbb { N}$$، اعداد $$M_ n > 0$$ به گونه‌ای وجود داشته باشند که

$$\large | f ( x ) | \le M _ n \;\;\;\;\; \forall x \in E$$

 اگر سری $$\sum _ { n = 1 } ^ \infty M _ n$$ همگرا شود، آنگاه سری $$\sum _ { n = 1 } ^ \infty f _ n$$ به صورت یکنواخت روی $$E$$ همگرا می‌شود.

اثبات لم: $$\epsilon > 0$$ را در نظر بگیرید. معیار کوشی برای همگرایی یک سری بیان می‌کند که $$N\in \mathbb { N}$$ وجود دارد به گونه‌ای که برای همه $$n . m \ge N$$ با $$n < m$$، داریم:

$$\large \left | M _ { n + 1 } + M _ { n + 2 } + \cdots + M _ { m } \right | = M _ { n + 1 } + M _ { n + 2 } + \cdots + M _ { m } < \epsilon$$

در نتیجه، برای همه $$n , m \ge N$$ با $$n < m$$ برای همه $$x \in E$$، داریم:

$$\large \left | \sum _ { i = 1 } ^ { m } f _ { i } ( x ) -\sum _ { i = 1 } ^ { n } f _ { i } ( x ) \right | = \left | f _ { n + 1 } ( x ) + \cdots + f _ { m } ( x ) \right | \\ \large \leq \left | f _{ n +1 } ( x ) \right | + \cdots + \left | f _ { m } ( x ) \right | \leq M _ { n + 1 } + \cdots + M _ { m } < \epsilon$$

دنباله مجموع جزئی $$( \sum _ { i = 1 } ^ n f _ i ) _ { n \in \mathbb{N}}$$ در معیار کوشی توابع صدق می‌کنند. بنابراین، طبق فرضی که گفتیم، می‌دانیم این مجموع‌های جزئی به صورت یکنواخت به سری $$\sum _ { n = 1 } ^ \infty f _ n$$ میل می‌کنند.

اثبات قضیه: از آنجا که $$| a ^ n \cos ( b ^ n \pi x ) | \le a ^ n$$ برای همه $$x \in \mathbb { R}$$ و $$\sum _ { n = 0 } ^ \infty a ^ n$$ همگرا می‌شود، سری با آزمون M وایرشتراس به صورت یکنواخت همگرا خواهد شد. علاوه بر این، از آنجا که مجموع‌های جزئی پیوسته هستند (مانند مجموع‌های متناهی توابع پیوسته)، حد یکنواخت $$f$$ نیز پیوسته است.

برای اینکه ببینیم $$f$$ در هیچ‌ جایی مشتق‌پذیر نیست، برای هر $$x _ 0 \in \mathbb { R}$$، نشان خواهیم داد که

$$\large \lim _ { x \to x _ 0 } \frac{ f ( x ) - f ( x _ 0 )} { x - x _ 0 }$$

وجود ندارد. به طور خاص، نشان می‌دهیم که وقتی $$x$$ از چپ و راست به $$x _ 0$$ میل کند، تفاضل خارج قسمت‌ به صورت گستره بین مقادیر مثبت و منفی بزرگ و بزرگ‌تر نوسان می‌کند.

نقطه ثابت $$x _ 0 \in \mathbb { R}$$ را در نظر بگیرید. برای هر $$m \in \mathbb { N}$$، فرض کنید $$\alpha _ m \in \mathbb { Z}$$ به گونه‌ای باشد که

$$\large b ^ { m } x _ { 0 } - \alpha _ { m } \in \left ( - \frac { 1 } { 2 } , \frac { 1 } { 2 } \right ]$$

عبارات زیر را تعریف می‌کنیم:

$$\large x _ { m } : = b ^ { m } x _ { 0 } - \alpha _ { m } \quad y _ { m } : = \frac { \alpha _ { m } - 1 } { b ^ { m } } \quad z _ { m } : = \frac { \alpha _ { m } + 1 } { b ^ { m } }$$

می‌بینیم که

$$\large y _ { m } - x _ { 0 } = - \frac { 1 + x _ { m } }{ b ^ { m } } < 0 < \frac { 1 - x _ { m } } { b ^ { m } } = z _ { m } - x _ { 0 }$$

بنابراین، $$y _ m < x _ 0 < z _ m$$ است. در نتیجه، داریم:

$$\large \lim _ { m \rightarrow \infty } \left | y _ { m } -x _ { 0 } \right | = \lim _ { m \rightarrow \infty } x _ { 0 } - y _ { m } = \lim _ { m \rightarrow \infty } \frac { 1 + x _ { m } }{ b ^ { m } } = 0$$

و

$$\large \lim _ { m \rightarrow \infty } \left | z _ { m } -x _ { 0 } \right | = \lim _ { m \rightarrow \infty } z _ { m } - x _ { 0 } = \lim _ { m \rightarrow \infty } \frac { 1 - x _ { m } } { b ^ { m } } = 0$$

این یعنی $$( y _ m ) _ { m \in \mathbb {N}}$$ و $$(z _ m ) _ { m \in \mathbb {N}}$$ دنباله‌هایی هستند که به ترتیب، به راست و چپ $$x _ 0$$ همگرا می‌شوند. تفاضل‌ خارج قسمت را برای $$f$$ در $$x = y _ m , m \in \mathbb { N}$$ و $$x = z _ m , m \in \mathbb { N}$$ بررسی می‌کنیم. ابتدا، داریم:

$$\large \begin {aligned} \frac { f \left ( y _ { m } \right ) - f \left ( x _ { 0 } \right ) } { y _ { m } - x _ { 0 } } & = \frac { \sum _ { n = 0 } ^ { \infty } a ^ { n } \cos \left ( b ^ { n } \pi y _ { m } \right ) - \sum _ { n = 0 } ^ { \infty } a ^ { n } \cos \left ( b ^ { n } \pi x _ { 0 } \right ) } { y _ { m } - x _ { 0 } } \\ & = \sum _ { n = 0 } ^ { \infty } a ^ { n } \frac { \cos \left ( b ^ { n } \pi y _ { m } \right ) - \cos \left ( b ^ { n } \pi x _ { 0 } \right ) } { y _ { m } - x _ { 0 } } \\ & = \sum _ { n = 0 } ^ { m - 1 } ( a b ) ^ { n } \frac { \cos \left ( b ^ { n } \pi y _ { m } \right ) - \cos \left ( b ^ { n } \pi x _ { 0 } \right ) } { b ^ { n } \left ( y _ { m } - x _ { 0 } \right ) } + \sum _ { n = 0 } ^ { \infty } a ^ { n + m } \frac { \cos \left ( b ^ { n + m } \pi y _ { m } \right ) - \cos \left ( b ^ { n + m } \pi x _ { 0 } \right ) } { y _ { m } - x _ { 0 } } \end {aligned}$$

دو مجموع آخر عبارت بالا را به ترتیب، $$S _ 1$$ و $$S_ 2$$ می‌نامیم. نشان خواهیم داد که $$S_ 1$$ کوچک و $$S_ 2$$ بزرگ است. با استفاده از ویژگی (د) بالا، داریم:

$$\large \begin {aligned} S _ { 1 } & = \sum _ { n = 0 } ^ { m - 1 } ( a b ) ^ { n } \frac { - 2 } { b ^ { n } \left ( y _ { m } - x _ { 0 } \right ) } \sin \left ( \frac { b ^ { n } \pi \left ( y _ { m } + x _ { 0 } \right ) } { 2 } \right ) \sin \left ( \frac { b ^ { n } \pi \left ( y _ { m } - x _ { 0 } \right ) } { 2 } \right ) \\ & = \sum _ { n = 0 } ^ { m - 1 } - \pi ( a b ) ^ { n } \sin \left ( \frac { b ^ { n } \pi \left ( y _ { m } + x _ { 0 } \right ) } { 2 } \right ) \frac { \sin \left ( \frac { b ^ { n } \pi \left ( y _ { m } - x _ { 0 } \right ) } { 2 } \right ) } { \frac { \pi b ^ { n } \left ( y _ { m } - x _ { 0 } \right ) } { 2 } } \end {aligned}$$

با استفاده از نامساوی مثلثی و ویژگی‌های (ب) و (ج)، می‌توان نوشت:

$$\large \left | S _ { 1 } \right | \leq \sum _ { n = 0 } ^ { m - 1 } \pi ( a b ) ^ { n } 1 \cdot 1 = \pi \frac { ( a b ) ^ { m } - 1 } { a b - 1 } < \pi \frac { ( a b ) ^ { m } } { a b - 1 }$$

بنابراین، $$\epsilon _ 1 \in ( - 1 , 1 )$$ وجود دارد به گونه‌ای که $$S_ 1 = \epsilon _ 1 \frac { \pi ( ab) ^ m } { ab - 1 }$$.

در ادامه، $$S_ 2$$ را بررسی می‌کنیم. ابتدا می‌دانیم $$y _ m = \frac {\alpha _ m - 1 } { b ^ m }$$ که $$\alpha _ m$$ یک عدد صحیح و $$b$$ یک عدد صحیح فرد است. بنابراین:

$$\large \cos \left ( b ^ { n + m } \pi y _ { m } \right ) = \cos \left ( b ^ { n } \pi \left ( \alpha _ { m } - 1 \right ) \right ) = ( - 1 ) ^ { b ^ { n } ( a - 1 ) } = ( - 1 ) ^ { \alpha _ { m } - 1 } = - ( - 1 ) ^ { \alpha _ { m } }$$

همچنین، با توجه به $$x _ m = b ^ m x _ 0 - \alpha _ m$$، از ویژگی (ه) می‌توان نتیجه گرفت:

$$\large \begin {aligned} \cos \left ( b ^ { n + m } \pi x _ { 0 } \right ) & = \cos \left ( b ^ { n } \pi \left ( x _ { m } + \alpha _ { m } \right ) \right ) \\ & = \cos \left ( b ^ { n } \pi x _ { m } \right ) \cos \left ( b ^ { n } \pi \alpha _ { m } \right ) - \sin \left ( b ^ { n } \pi x _ { m } \right ) \sin \left ( b ^ { n } \pi \alpha _ { m } \right ) \\ & = ( - 1 ) ^ { b ^ { n } \alpha _ { m } } \cos \left ( b ^ { n } \pi x _ { m } \right ) - 0 \\ & = ( - 1 ) ^ { b ^ { n } \alpha _ { m } } \cos \left ( b ^ { n } \pi x _ { m } \right ). \end {aligned}$$

با استفاده از این محاسبات، داریم:

$$\large \begin {aligned} S _ { 2 } & = \sum _ { n = 0 } ^ { \infty } a ^ { n + m } \frac { - ( - 1 ) ^ { \alpha _ { m } } - ( - 1 ) ^ { \alpha _ { m } } \cos \left ( b ^ { n } \pi x _ { m } \right ) } { y _ { m } - x _ {0 } } \\ & = \sum _ { n = 0 } ^ { \infty } a ^ { n + m } ( - 1 )( - 1 ) ^ { \alpha _ { m } } \frac { 1 + \cos \left ( b ^ { n } \pi x _ { m } \right ) } { - \frac { 1 + x _ { m } } { b ^ { m } } } \\ & = ( a b ) ^ { m } ( - 1 ) ^ { \alpha _ { m } } \sum _ { n = 0 } ^ { \infty } a ^ { n } \frac { 1 + \cos \left ( b ^ { n } \pi x _ { m } \right ) } { 1 + x _ { m } } \end {aligned}$$

با توجه به اینکه $$x _ m \in ( - \frac {1} { 2 } , \frac 12 ]$$، جملات این مجموع در عبارت آخر نامنفی هستند. در نتیجه:

$$\large \sum _ { n = 0 } ^ { \infty } a ^ { n } \frac { 1 + \cos \left ( b ^ { n } \pi x_ { m } \right ) } { 1 + x _ { m } } \geq \frac { 1 + \cos \left ( \pi x _ { m } \right ) } { 1 + x _ { m } } \geq \frac { 1 } { 1 + \frac { 1 } { 2 } } = \frac { 2 } { 3 }$$

بنابراین، $$\eta _ 1 \ge 1$$ به گونه‌ای وجود دارد که $$S _ { 2 } = ( a b ) ^ { m } ( - 1 ) ^ { \alpha _ { m } } \eta _ { 1 } \frac { 2 } { 3 }$$.

با قرار دادن محاسبات $$S_ 1$$ و $$S_ 2$$، خواهیم داشت:

$$\large \begin {aligned} \frac { f \left ( y _ { m } \right ) - f \left ( x _ { 0 } \right ) } { y _ { m } - x _ { 0 } } = S _ { 1 } + S _ { 2 } & = \epsilon _ { 1 } \frac { \pi ( a b ) ^ { m } } { a b - 1 } + ( a b ) ^ { m } ( - 1 ) ^ { \alpha _ { m } } \eta _ { 1 } \frac { 2 } { 3 } \\ & = ( - 1 ) ^ { \alpha _ { m } } ( a b ) ^ { m } \eta _ { 1 } \left ( \frac { 2 } { 3 } + ( - 1 ) ^ { \alpha _ { m } } \frac { \epsilon _ { 1 } } { \eta _ { 1 } } \frac { \pi } { a b - 1 } \right ) \end {aligned}$$

به فرض $$ab > 1 + \frac {3 \pi } {2 }$$ باز می‌‌گردیم که معادل با $$\frac { \pi}{ab - 1 } < \frac 2 3$$ است. با استفاده از $$\epsilon _ 1 | < 1$$ و $$\eta \ge 1$$، داریم:

$$\large \frac { 2 } { 3 } + ( - 1 ) ^ { \alpha _ { m } } \frac { \epsilon _ { 1 } } { \eta _ { 1 } } \frac { \pi } { a b - 1 } > \frac { 2 } { 3 } - \frac { \pi } { a b - 1 } > 0$$

در نتیجه، علامت $$\frac { f \left ( y _ { m } \right ) - f \left ( x _ { 0 } \right ) } { y _ { m } - x _ { 0 } }$$ با $$( - 1 ) ^ {\alpha _ m }$$ کاملاً تعیین می‌شود و

$$\large \left | \frac { f \left ( y _ { m } \right ) - f \left ( x _ { 0 } \right ) } { u _ { m } - x _ { 0 } } \right | > ( a b ) ^ { m } \left ( \frac { 2 } { 3 } - \frac { \pi } { a b - 1 } \right )$$

بنابراین، نه تنها علامت‌ تفاضل خارج قسمت سریعاً تغییر می‌کند، بلکه اندازه آن وقتی $$m \to \infty$$، به مثبت بینهایت میل می‌کند. از آنجا که $$\lim _ {m \to \infty} y _ m = x _ 0$$، کافی است نشان دهیم $$\lim _ { x \rightarrow x _ { 0 } } \frac { f \left ( y _ { m } \right ) - f \left ( x _ { 0 } \right ) } { y _ { m } - x _ { 0 } }$$ وجود ندارد. همچنین، نشان خواهیم داد که رفتار مشابهی برای $$( z _ m ) _ { m \in \mathbb{N}}$$ رخ می‌دهد.

مشابه آنچه پیش‌تر گفتیم، می‌توان نوشت:

$$\large \frac { f \left ( z _ { m } \right ) - f \left ( x _ { 0 } \right ) } { z _ { m } - x _ { 0 } } = S _ { 1 } ^ { \prime } + S _ { 2 }$$

و عبارت مشابه $$S _ 1 ^ \prime = \epsilon _ 2 \frac {\pi (ab)^ m }{ ab - 1 }$$ برای $$\epsilon _ 2 \in (-1 , 1 )$$ به دست می‌آید. با استفاده از $$z _ m - x _ 0 = \frac { 1 - x _ m } { b ^ m }$$، داریم:

$$\large \begin {aligned} S _ { 2 } ^ { \prime } & = \sum _ { n =0 } ^ { \infty } a ^ { n + m } \frac { - ( - 1 ) ^ { \alpha _ { m } } - ( - 1 ) ^ { \alpha _ { m } } \cos \left ( b ^ { n } \pi x _ { m } \right ) } { \frac { 1 - k _ { m } } { b _ { m } } } \\ & = - ( a b ) ^ { m } ( - 1 ) ^ { \alpha _ { m } } \sum _ { n = 0 } ^ { \infty } a ^ { n } \frac { 1 + \cos \left ( b ^ { n } \pi x _ { m } \right ) } { 1 - x _ { m } } \end {aligned}$$

از آنجا که $$x _ m \in ( - \frac { 1 } { 2 } , \frac 12 ]$$، جملات در مجموع در آخرین عبارت نامنفی هستند. در نتیجه:

$$\large \sum _ { n = 0 } ^ { \infty } a ^ { n } \frac { 1 + \cos \left ( b ^ { n } \pi x _ { m } \right ) } { 1 - x _ { m } } \geq \frac { 1 + \cos \left ( \pi x _ { m } \right ) } { 1 - x _ { m } } > \frac { 1 } { 1 - \left ( - \frac { 1 } { 2 } \right ) } = \frac { 2 } { 3 }$$

بنابراین، $$\eta_{2} \geq 1$$ به گونه‌ای وجود دارد که $$S _ { 2 } ^ { \prime } = - ( a b ) ^ { m } ( - 1 ) ^ { \alpha _ { m } } \eta _ { 2 } \frac { 2 } { 3 }$$. در نتیجه، خواهیم داشت:

$$\large \begin {aligned} \frac { f \left ( z _ { m } \right ) - f \left ( x _ { 0 } \right ) } { z _ { m } - x _ { 0 } } = S _ { 1 } ^ { \prime } + S _ { 2 } ^ { \prime } & = \epsilon _ { 2 } \frac { \pi ( a b ) ^ { m } } { a b - 1 } - ( - 1 ) ^ { a _ { m } } ( a b ) ^ { m } \eta _ { 2 } \frac { 2 } { 3 } \\ & = - ( - 1 ) ^ { a _ { - } } ( a b ) ^ { m } \eta _ { 2 } \left ( \frac { 2 } { 3 } - ( - 1 ) ^ { \alpha _ { m } } \frac { \epsilon _ { 2 } } { \eta _ { 2 } } \frac { \pi } { a b - 1 } \right ) \end {aligned} .$$

مانند قبل، داریم:

$$\large \frac { 2 } { 3 } - ( - 1 ) ^ { \alpha _ m } \frac { \epsilon _ 2 } { \eta _ { 2 } } \frac { \pi } { a b - 1 } > \frac { 2 } { 3 } - \frac { \pi } { a b - 1 } > 0,$$

در نتیجه، علامت $$\frac { f \left ( z _ { m } \right ) - f \left ( x _ { 0 } \right ) } { z _ { m } - x _ { 0 } }$$ با $$- ( - 1 ) ^ {\alpha _ m}$$ کاملاً تعیین می‌شود. همچنین، داریم:

$$\large \left | \frac { f \left ( z _ { m } \right ) -f \left ( x _ { 0 } \right ) } { z _ { m } - x _ { 0 } } \right | > ( a b ) ^ {m } \left ( \frac { 2 } { 3 } - \frac { \pi } { a b - 1 } \right ) \stackrel { m \rightarrow \infty } { \rightarrow } + \infty$$

بنابراین، رفتار مشابهی برای سمت راست $$x _ 0$$ رخ می‌دهد.

نمودار تابع وایرشتراس

نمودار تابع وایرشتراس برای جمله $$n = 0$$، یعنی $$\cos ( \pi x )$$ در شکل زیر نشان داده شده است.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل مساله در فرادرس

کلیک کنید

جملات مرتبه بالاتر نوسان‌های کوچک‌تری به وجود می‌آورند.

با انتخاب دقیق $$b$$ مانند قضیه بالا، نمودار بسیار ناهموار می‌شود و هیچ انتخاب منطقی برای یک خط مماس در هیچ نقطه‌ای وجود ندارد و تابع در هیچ جایی مشتق‌پذیر نیست.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضیات عمومی 1
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضی پایه دانشگاهی
• توابع صعودی و نزولی — به زبان ساده
• مجانب تابع — به زبان ساده
• توابع محدب و مقعر — از صفر تا صد

^^