پخش بار اقتصادی – از صفر تا صد

در آموزش‌های پیشین مجله فرادرس، با مفاهیم پخش بار و حل مسئله پخش بار با استفاده از روش‌های نیوتن-رافسون و گاوس-سایدل آشنا شدیم. در این آموزش، مسئله پخش بار اقتصادی (Economic Dispatch) را معرفی می‌کنیم.

پیچیدگی ارتباط و اندازه ناحیه‌های مختلف سیستم‌های قدرت که به صورت هماهنگ کنترل می‌شوند، به سرعت در حال افزایش است. این توسعه مستلزم تخصیص بهینه توان الکتریکی تولیدی تعداد زیادی از ژنراتورهای سیستم است.

اینکه یک ژنراتور در تسهیم بار در یک بازه زمانی مشخص شرکت داشته باشد، یک تعهد است که باید انجام شود. پس از آنکه مسئله تعهد واحد تولیدی حل شد، مسئله به مسئله تخصیص بهینه ژنراتورهای موجود تبدیل می‌شود تا تقاضای بار پیش‌بینی شده را در بازه زمانی فعلی برآورده کند.

در یک مرکز مدیریت انرژی پیشرفته و به‌روز، از روش‌های بهینه‌سازی نه‌تنها برای تعیین توان خروجی بهینه ژنراتورهای موجود، بلکه برای تنظیمات بهینه دستگاه‌های کنترلی مختلف، مانند تنظیمات تپ‌چنجرهای بار (Load Tap Changers) یا LTCها، خروجی تجهیزات جبرانساز توان راکتیو، تنظیمات مطلوب جابه‌جاکننده‌های فاز و غیره استفاده می‌شود.

هدف مطلوب مسائل بهینه‌سازی این‌چنینی، می‌تواند موارد مختلفی مانند کمینه‌سازی هزینه تولید، کمینه‌سازی کل تلفات توان سیستم، کمینه‌سازی تغییرات ولتاژ، و بیشینه‌سازی قابلیت اطمینان توان داده شده به مصرف‌کنندگان باشد.

یک یا چند مورد از این اهداف را می‌توان در هنگام فرمول‌بندی استراتژی بهینه‌سازی در نظر گرفت. تعیین توان حقیقی ژنراتورها به گونه‌ای که هزینه تولید در سیستم کمینه شود، به طور سنتی به عنوان مسئله پخش بار اقتصادی (Economic Load Dispatch) یا ELD شناخته می‌شود.

بخش اعظم سیستم‌های تولید انرژی الکتریکی مشتمل بر سه نوع هستند: هسته‌ای، برق‌آبی و حرارتی (سوخت آن‌ها زغال‌سنگ، نفت یا گاز است). نیروگاه‌های هسته‌ای معمولاً توان خروجی ثابتی تولید می‌کنند. هزینه عملیات واحدهای برق‌آبی نیز، معمولاً با تغییر توان خروجی تغییر زیادی نمی‌کند. بنابراین، در این آموزش، درباره مسئله پخش بار اقتصادی سیستم‌های قدرتی بحث می‌کنیم که شامل چند واحد تولید برق حرارتی باشند.

مسئله پخش بار اقتصادی بدون در نظر گرفتن تلفات انتقال

ابتدا مسئله پخش بار اقتصادی را با چشم‌پوشی از تلفات خط انتقال فرمول‌بندی می‌کنیم. این فرض معمولاً‌ در صورتی اتخاذ می‌شود که دسته‌ای از ژنراتورها، مانند واحدهای تولیدی یک نیروگاه به یک شین متصل شده باشند یا وقتی که این واحدها بسیار نزدیک به هم باشند.

این امر، نادیده گرفتن تلفات انتقال را به دلیل فاصله کم تضمین می‌کند. پیکربندی چنین سیستمی در شکل ۱ نشان داده شده است، که در آن، $$N$$ واحد حرارتی به یک شین متصل شده‌اند که بار $$P _ \text{load}$$ را تغذیه می‌کند. ورودی هر واحد برحسب نرخ هزینه (دلار بر ساعت یا h/$) توصیف می‌شود. نرخ هزینه کل، برابر با مجموع توان‌های خروجی است که باید برابر با بار باشد (توجه کنید که در اینجا از تلفات توان صرف‌نظر شده است).

$$N$$ واحد حرارتی به یک شین برای تغذیه بار $$P _ \text{load}$$ متصل شده‌اند. " width="466" height="360">

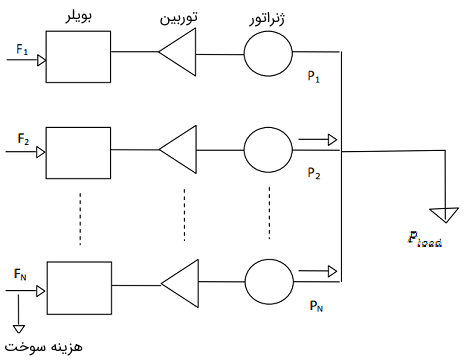
مشخصه هزینه سوخت

مسئله پخش بار اقتصادی در واقع تعیین سطوح تولیدی است که در آ‌ن‌ها هزینه تولید کل برای یک سطح مشخص بار کمینه شود. در واحدهای تولید حرارتی، هزینه سوخت با تغییر توان خروجی واحد به اندازه قابل توجهی تغییر می‌کند. بنابراین، لازم است مشخصه هزینه سوخت ژنراتورها را با یافتن خروجی‌های توان حقیقی بهینه در نظر بگیریم.

یک مشخصه هزینه سوخت رایج در شکل ۲ نشان داده شده است.

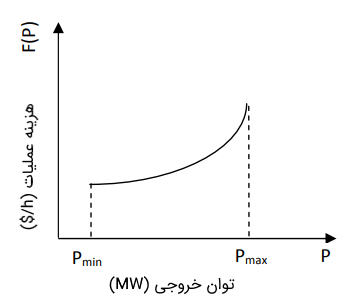
به طور کلی، هزینه‌های نیروی کار، تأمین و نگهداری ثابت هستند. $$P_\text{min}$$ سطحی از خروجی است که توان کمتر از آن غیراقتصادی است یا از نظر فنی برای عملیات واحدها ممکن نیست. $$P_\text{max}$$ کران توان خروجی بیشینه است. برای فرمول‌بندی مسئله پخش بار اقتصادی، هزینه‌های سوخت معمولاً به صورت یک تابع درجه دوم از توان خروجی نشان داده می‌شود:

$$\large F ( P ) = a P ^ 2 + b P + c \;\;\;\;\; ( 1 )$$

فرمول‌بندی مسئله

هزینه سوخت کل عملیات $$N$$ ژنراتور به صورت زیر بیان می‌شود:

$$\large \begin {align*} F _ T & = F _ 1 ( P _ 1 ) + F _ 2 ( P _ 2 ) + \cdots + F _ N ( P _ N) \\ & = \sum _ { i = 1 } ^ { N } F _ i ( P _ i ) \end {align*} \;\;\;\;\; ( 2 )$$

با صرف‌نظر کردن از تلفات انتقال، کل تولید باید کل بار را تغذیه کند. بنابراین، قید تساوی زیر را داریم:

$$\large \sum _ { i = 1 } ^ { N} { P _ i } = P _ \text{load} \;\;\;\;\; ( 3 )$$

براساس محدودیت‌های کمینه و بیشینه توان ژنراتورها، قیود نامساوی زیر را نیز داریم:

$$\large P _ {i , \text{min} } \le P _ i \le P _ {i , \text{max} } \;\;\;\;\;\;\; \forall i = 1 , 2 , \ldots , N . \;\;\;\;\; ( 4 )$$

این یک مسئله بهینه‌سازی مقید است که می‌توان آن را با روش ضرایب لاگرانژ‌ حل کرد. روش لاگرانژ به صورت زیر فرمول‌بندی می‌شود:

$$\large \mathcal { L } = F _ T + \lambda \phi \;\;\;\;\; ( 5 )$$

که در آن، $$\phi = P _ \text{load} - \sum _{i=1}^{N} P_ i$$ قید تساوی (۳)‌ را نشان می‌دهد و $$\lambda$$ ضریب لاگرانژ است. شرط لازم برای آنکه $$F_ T$$ کمینه شود، این است که مشتق تابع لاگرانژ نسبت به هر یک از متغیرهای مستقل برابر با صفر شود. در نتیجه، شرایط لازم مسئله بهینه‌سازی به صورت زیر خواهد بود:

$$\large \begin {aligned} \frac { \partial \mathcal { L } } { \partial P _ { i } } & = \frac { \partial } { \partial P _ { i } } \left \{ \sum _ { i = 1 } ^ { N } F _ { i } \left ( P _ { i } \right ) + \lambda \left ( P _ { \text {load } } - \sum _ { i = 1 } ^ { N } P _ { i } \right ) \right \} \\ & = \frac { \partial F _ { i } } { \partial P _ { i } } - \lambda = 0 ; \forall i = 1 , 2 , \ldots , N \end {aligned} \;\;\;\;\; (6 )$$

و

$$\large \frac {\partial \mathcal { L } } { \partial \lambda } = \phi = 0 . \;\;\;\;\; ( 7 )$$

با بازنویسی (۶)، داریم:

$$\large \frac { \partial F _ { i } } { \partial P _ { i } } = \lambda ; \forall i = 1 , 2 , \ldots , N \;\;\;\;\; ( 8 )$$

معادله (۸)‌ بیان می‌کند که برای کمینه کردن هزینه سوخت، شرط لازم این است که هزینه‌های سوخت اضافی با هم برابر باشند. معادله (۸)، همراه با (۳)‌ و (۴)، معادلات هماهنگی (Coordination Equations) برای پخش بار اقتصادی بدون در نظر گرفتن تلفات شبکه نامیده می‌شوند.

تذکر: با استفاده از معادله (۱)، مشخصه هزینه سوخت همه ژنراتورها به صورت زیر بیان می‌شود:

$$\large F_ i = a _ i P _ i ^ 2 + b _ i P _ i + c _ i ; \;\;\;\forall i = 1, 2 , \ldots . N . \;\;\;\;\; (9 )$$

با استفاده از (۸)، شرایط لازم برای جواب‌های بهینه به صورت زیر داده می‌شود:

$$\large \frac { \partial F _ i } { \partial P _ i } = 2 a _ i P _ i + b _ i = \lambda ; \;\;\; \forall i = 1 , 2 , \ldots , N . \;\;\;\;\; ( 10 )$$

یا

$$\large P_ i = \frac { \lambda - b _ i } { 2 a _ i } ; \;\;\; \forall i = 1 , 2 , \ldots , N . \;\;\;\;\; ( 11 )$$

با جایگذاری $$P_ i$$ در رابطه (۳)، داریم:

$$\large \sum _ { i = 1 } ^ { N} \frac { \lambda - b _ i } { 2 a _ i } = P _ \text{load}$$

یا

$$\large \lambda = \left [ \frac { P _ \text{load} + \sum _ { i = 1 } ^ { N} ( b _ i / 2 a _ i )} { \sum _ {i=1} ^ { N} ( 1 / 2 a _ i )} \right ] . \;\;\;\;\; ( 12 )$$

در نتیجه، $$\lambda$$ را می‌توان با (۱۰) به دست آورد و پس از آن،‌ $$P_ i , \; i = 1 , 2 , \ldots , N$$ را از (۹) محاسبه کرد.

مثال ۱

دو واحد تولیدی برق در یک سیستم قدرت، دارای منحنی‌های هزینه زیر هستند (این هزینه‌ها فقط برای نمونه هستند و هزینه‌های واقعی یک سیستم قدرت را نشان نمی‌دهند):

$$\large \begin {aligned} & F _ { 1 } \left ( P_ { 1 } \right ) = 0 . 0 5 P _ { 1 } ^ { 2 } + 2 2 P _ { 1 } + 1 2 0 \\ & F _ { 2 } \left ( P _ { 2 } \right ) = 0 . 0 6 P _ { 2 } ^ { 2 } + 1 6 P _ { 2 } + 1 2 0 \end {aligned}$$

$$P_ 1$$ و $$P_ 2$$ برحسب مگاوات هستند. هر دو واحد به صورت تمام وقت کار می‌کنند. حداکثر و حداقل بار هر واحد نیز، به ترتیب، $$100 \, \text{MW}$$ و $$20 \, \text{MW}$$ است. پخش بار اقتصادی واحدها را برای تغذیه بار $$80 \, \text{MW}$$، با چشم‌پوشی از تلفات خطوط انتقال، انجام دهید.

حل: با استفاده از رابطه (۱۰)،‌ داریم:

$$ \large \begin {align*}<br /> \lambda & = \frac { 80 + ( \frac {22}{2 \times 0.05}) + ( \frac { 16 }{ 2 \times 0.06 } ) } { ( \frac { 1 } { 2 \times 0.05 }) + ( \frac { 1 }{ 2 \times 0.06 } ) } \\<br /> & = ( 80 + 353. 33 ) / 18. 33 = 23.64 \; $ / \text{MWh}<br /> \end {align*} $$

در نتیجه، با استفاده از (۹)، خواهیم داشت:

$$\large \begin {align*} P _ 1 & = \frac { 23.64-22}{ 2 \times 0.05 } = 16.36 \; \text{MW} \\ P _ 2 & = \frac { 23.64 - 16 } { 2 \times 0.06 } = 63.64 \; \text{MW} \end {align*}$$

با توجه به اینکه $$P _{1,\text{min}} = 20 \; \text{MW}$$ است، $$P_1$$ را در مقدار ثابت $$20\; \text{MW}$$ قرار می‌دهیم و باقیمانده تقاضا توسط $$P_ 2$$ تأمین می‌شود. در نهایت، پخش بار اقتصادی به صورت زیر خواهد بود:

$$\large \begin {align*} P _ 1 & = 20 \; \text{MW} \\ P _ 2 & = 80 - 20 = 60 \; \text{MW} \end {align*}$$

پخش بار اقتصادی با استفاده از روش گرادیان

اساس روش گرادیان این است که کمینه تابع $$f ( x )$$ را می‌توان با دنباله‌ای از گام‌ها در جهت حداکثر شیب $$f ( x )$$ به دست آورد. بنابراین، جست‌وجو باید در جهت $$- \nabla f$$ باشد. در مسئله پخش بار اقتصادی ، هدف، کمینه کردن کل هزینه تولید است:

$$\large F _ T = \sum _ {i = 1 } ^ {N} F _ i ( P _ i )$$

قید تساوی نیز به صورت زیر است:

$$\large \sum _ {i = 1 } ^ {N} P _ i = P _ \text{load}$$

با توجه به رابطه (۵)، تابع لاگرانژ را می‌توان به صورت زیر تشکیل داد:

$$\large \mathcal { L } = \sum _ { i = 1 } ^ { N } F _ i ( P _ i ) + \lambda ( P _ \text{load} - \sum _ { i = 1 } ^{ N} P _ i )$$

اکنون، گرادیان تابع لاگرانژ را می‌نویسیم:

$$\large \nabla \mathcal { L } = \left [ \begin {array} { c } { \frac { \partial \mathcal { L } } { \partial P _ { 1 } } } \\ { \frac { \partial \mathcal { L } } { \partial P _ { 2 } } } \\ { \vdots } \\ { \frac { \partial \mathcal { L } } { \partial P _ { N } } } \\ { \frac { \partial \mathcal { L } } { \partial \lambda } } \end {array} \right ] = \left [ \begin {array} { c } { \frac { \partial F _ { 1 } } { \partial P _ { 1 } } - \lambda } \\ { \frac { \partial F _ { 2 } } { \partial P _ { 2 } } - \lambda } \\ { \vdots } \\ { \frac { \partial E _ { N } } { \partial P _ { N } } - \lambda } \ \ { P _ { \mathrm {load} } - \sum _ { i = 1 } ^ { N } P _ { i } } \end {array} \right ] \;\;\;\;\; (13)$$

و معادله تکراری به صورت زیر خواهد بود:

$$\large \mathbf { x } ^ n = \mathbf { x } ^ { n - 1 } - \varepsilon \nabla \mathcal { L } \;\;\;\;\; (14)$$

که در آن،

$$\large \mathbf { x } ^ { n } = \left [ \begin {array} { c } { P _ { 1 } ^ { ( n ) } } \\ { P _ { 2 } ^ { ( n ) } } \\ { \vdots } \\ { P _ { N } ^ { ( n ) } } \\ { \lambda ^ { ( n ) } } \end {array} \right ] \;\;\;\;\; ( 1 5)$$

و

$$\large \mathbf { x } ^ { n - 1 } = \left [ \begin {array} { c } { P _ { 1 } ^ { ( n - 1 ) } } \\ { P _ { 2 } ^ { ( n - 1 ) } } \\ { \vdots } \\ { P _ { N } ^ { ( n - 1 ) } } \\ { \lambda ^ { ( n - 1 ) } } \end {array} \right ] \;\;\;\;\; ( 1 6 )$$

الگوریتم پخش بار اقتصادی با استفاده از روش گرادیان

گام ۱: مقادیر اولیه $$P_1 ^{(0)}$$، $$P_2^{(0)}$$، ...، $$P_N^{(0)}$$ را انتخاب کنید، به طوری که $$\sum _ { i = 1 } ^ { N} { P _ i ^ { ( 0 )}} = P _ \text{load}$$.

گام ۲: مقدار اولیه $$\lambda _ i ^ { ( 0 )}$$ را برای هر ژنراتور حساب کنید:

$$\large \lambda _ { i } ^ { ( 0 ) } = \left . \frac { \partial F _ { i } \left ( P _ { i } \right ) } { \partial P } \right | _ { P _ { i } ^ { ( 0 ) } } ; \forall i = 1 , 2 , \ldots , N$$

گام ۳: هزینه اضافی متوسط اولیه را محاسبه کنید:

$$\lambda ^ { ( 0 )} = \left ( \frac { 1 } { N } \right ) \sum _ { i = 1 } ^ { N } \lambda _ i ^ 0$$

گام ۴: $$\nabla \mathcal {L}$$ را محاسبه کنید.

گام ۵: اگر $$| \nabla L | \le \delta$$، آنگاه به گام ۸ بروید، در غیر این‌صورت به مرحله ۶ بروید ($$\delta$$ یک مقدار کوچک از پیش تعریف شده است).

گام ۶: مقدار $$\mathbf { x } ^ { ( i ) } = \left [ P _ { 1 } ^ { ( i ) } , P _ { 2 } ^ { ( i ) } , \ldots , P _ { N } ^ { ( i ) } , \lambda ^ { ( i ) } \right ] ^ { \mathrm { T } } = \mathbf { x } ^ { ( i - 1 ) } + \varepsilon \nabla \mathcal { L }$$ را به‌روزرسانی کنید.

گام ۷: به گام ۴ بروید.

گام ۸: توقف.

پخش بار اقتصادی با در نظر گرفتن تلفات شبکه

این پخش بار اقتصادی برای نیروگاه‌های مختلف در یک سیستم قدرت انجام می‌شود.

شکل ۳ شماتیک چنین سیستمی را نشان می‌دهد. لازم به ذکر است که تلفات سیستم انتقال در اینجا در نظر گرفته می‌شود.

$$N$$ واحد که بار $$P_\text{load}$$ را از طریق شبکه انتقال تغذیه می‌کند." width="644" height="360">

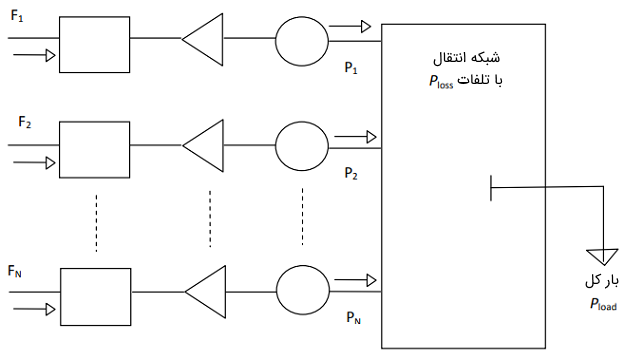
شکل ۳: $$N$$ واحد که بار $$P_\text{load}$$ را از طریق شبکه انتقال تغذیه می‌کند.در مثال ۱ دیدیم که برای یک توان خروجی مشخص، واحد ۱ در مقایسه با واحد ۲ هزینه اضافی بیشتری داشت. بنابراین، برای پخش بار اقتصادی، واحد ۲ به گونه‌ای برنامه‌ریزی شد که توان بیشتری از واحد ۱ تولید کند. همه این موارد در صورتی بود که واحدها بخشی از یک نیروگاه باشند یا به لحاظ موقعیت در نزدیکی یکدیگر باشند. اگر تلفات خط انتقال زیاد باشد (مثلاً به دلیل فاصله زیاد بین واحد تولیدی و بار)، برای واحدی با هزینه افزایشی کم، ممکن است هزینه عملیات بیشتر شود. بنابراین، در تعیین پخش بار اقتصادی واحدهای یک سیستم قدرت باید تلفات خطوط انتقال را در نظر گرفت.

نرخ هزینه سوخت کل، با توجه به رابطه (۲) به صورت زیر است:

$$\large F _ T = F _ 1 ( P _ 1 ) + F _ 2 ( P _ 2 ) + \cdots + F _ N ( P _ N) = \sum _ { i = 1 } ^ { N } F _ i ( P _ i ) .$$

معادله تعادل توان با در نظر گرفتن تلفات انتقال نیز به صورت زیر خواهد بود:

$$\large \phi = P _ \text{loss} + P _ \text{load} - \sum _{i = 1} ^ {N} P _ i = 0 \;\;\;\;\; (17)$$

که در آن، $$P _ \text{loss}$$ کل تلفات انتقال سیستم است. در این حالت، مسئله یافتن $$P_i$$ به گونه‌ای است که $$F_T$$ با در نظر گرفتن قید (۱۷) کمینه شود.

با استفاده از روش ضرایب لاگرانژ داریم:

$$\large \mathcal { L } = F _ T + \lambda \phi$$

که در آن، $$\phi$$ در رابطه (۱۷) تعریف شده است.

شرایط لازم برای کمینه کردن $$F_ T$$ به صورت زیر هستند:

$$\large \frac { \partial \mathcal { L } }{\partial P _ i } = 0 ; \;\; \forall i = 1 , 2 , \ldots , N$$

یا

$$\large \frac { \partial }{\partial P _ i } [\sum _ {i = 1 } ^ {N} F _ i ( P _ i ) + \lambda ( P_\text{loss} + P _\text{load} - \sum _{i=1} ^ { N} P _ i )] = 0$$

یا

$$\large \frac { \partial \mathcal {L}} {\partial P _ i } = \frac { \partial F_ i } {\partial P_i} + \lambda ( \frac {\partial P _\text{loss}}{\partial P_i} - 1 ) = 0 ; \;\; \forall i = 1 , 2 , \ldots , N. \;\;\;\;\; ( 18 )$$

با مرتب کردن معادله بالا، داریم:

$$\large \lambda = \frac {\frac {\partial F_i}{\partial P _ i } } {1 - \frac {\partial P_\text{loss}}{\partial P _ i }} . \;\;\;\;\; (19)$$

معادله بالا اغلب به صورت زیر نوشته می‌شود:

$$\large \lambda = P _ { \mathrm { f } i } \frac {\partial F_ i } {\partial P_ i } \;\;\;\;\;\; ( 20 )$$

که در آن، $$P _ { \mathrm { f } i }$$ عامل یا ضریب جریمه (Penalty Factor) نیروگاه نام دارد و به صورت زیر بیان می‌شود:

$$\large P _ { \mathrm { f } i } = \frac { 1 } { 1 - \frac { \partial P _ \text {loss} } {\partial P _ i} } \;\;\;\;\;\; ( 21 )$$

در اینجا، $$\frac { \partial P _ \text {loss} } {\partial P _ i}$$ تلفات افزایشی (Incremental Loss) برای شین $$i$$ است. معادله (۲۰) نشان می‌دهد که حداقل هزینه عملیات وقتی حاصل می‌شود که حاصل‌ضرب هزینه اضافی (IC) در ضریب جریمه مربوط به همه واحدهای سیستم با هم برابر باشند.

تذکر: در حالتی که همه واحدها مربوط به یک نیروگاه باشند یا ژنراتورها به یک شین متصل شده باشند، معادله (۲۰) به صورت زیر در خواهد آمد:

$$\large \lambda = P _ {\text { f } 1 } \frac { \partial F _ 1 } { \partial P _ 1 } = P _ {\text { f } 2 } \frac { \partial F _ 2 } { \partial P _ 2 } = \ldots = P _ {\text { f } N } \frac { \partial F _ N } { \partial P _ N } .$$

هنگامی که واحدها به یک شین متصل شده باشند، تغییر افزایشی تلفات انتقال و تغییر تولید برای همه واحدها یکسان خواهد بود. بنابراین:

$$\large P _ {\text { f } 1 } = P _ {\text { f } 2 } = \ldots =P _ {\text { f } N } .$$

در نتیجه، خواهیم داشت:

$$\large \frac { \partial F _ 1 } { \partial P_ 1 } = \frac { \partial F _ 2 } { \partial P_ 2 } = \ldots = \frac { \partial F _ N } { \partial P_ N } \;\;\;\;\; ( 22 )$$

که مشابه حالتی است که واحدها به یک شین متصل شده‌اند.

معادله‌های (۱۹) و (۱۷) معادلات هماهنگی پخش بار اقتصادی با در نظر گرفتن تلفات انتقال نامیده می‌شوند. حل مسئله پخش بار اقتصادی در این حالت، نسبت به وقتی که تلفات انتقال را در نظر نگرفتیم، کمی پیچیده است. دو رویکرد اصلی برای حل این مسئله وجود دارد: یکی فرمول تلفات شبکه و دیگری ابزارهای بهینه‌سازی برای معادلات پخش بار مقید.

معادله تلفات خط انتقال

معادله تلفات خط انتقال، با نام فرمول کاهش کرون (Kron’s Loss Formula) شناخته می‌شود و به صورت زیر است:

$$\large P _ { \text {loss } } = \mathbf { P } ^ { \mathrm { T } } \mathbf { B P } + \mathbf { B } _ { 0 } ^ { \mathrm { T } } \mathbf { P } + \mathbf { B } _ { 0 0 } \;\;\;\;\; ( 23 )$$

که در آن، $$\mathbf { P }$$ بردار همه خروجی‌های خالص همه ژنراتورها، $$\mathbf { B }$$ یک ماتریس مربعی، $$\mathbf { B} _ 0$$ برداری با طول مشابه $$\mathbf { P }$$ و $$\mathbf { B} _ {00}$$ یک ثابت است.

جملات $$\mathbf { B}$$ ضرایب تلفات یا ضرایب $$\mathbf {B}$$ نامیده می‌شوند. همچنین $$\mathbf { B}$$ یک ماتریس متقارن $$N \times N$$ است که با نام ماتریس $$\mathbf { B}$$ شناخته می‌شود.

معادله (۲۳) را می‌توان به صورت زیر نوشت:

$$\large P_\text{load} = \sum _ { i = 1 } ^ { N } \sum _ { j = 1 } ^ { N } P _ { i } B _ { i j } P _ { j } + \sum _ { i = 1 } ^ { N } B _ { i 0 } P _ { i } + B _ { 0 0 }. \ \;\;\;\;\; (24)$$

با توجه به معادله هماهنگی، قید تساوی به صورت زیر در می‌آید:

$$\large \phi = P _ { \text {load } } + \left [ \sum _ { i = 1 } ^ { N } \sum _ { j = 1 } ^ { N } P _ { i } B _ { i j } P _ { j } + \sum _ { i = 1 } ^ { N } B _ { i 0 } P _ { i } + B _ { 0 0 } \right ] - \sum _ { i = 1 } ^ { N } P _ { i }. \;\;\;\;\; (25)$$

اکنون مشتق تابع لاگرانژ برابر است با:

$$\large \frac { \partial \mathcal { L } } { \partial P _ i } = \frac { \partial F _ i } { \partial P _ i } - \lambda [ 1 - 2 \sum _ { j = 1 } ^ { N } B _ { i j } P _ j - B _ { i 0 } ] . \;\;\;\;\; ( 26 )$$

اکنون معادلات هماهنگی را با هم داریم و برای حل آن‌ها از روش‌هایی که در ادامه آمده‌اند استفاده می‌کنیم.

پخش بار اقتصادی با فرمول ماتریس $$\Large { B}$$

با توجه به رابطه (۱)، داریم:

$$\large F _ i = a _ i P _ i ^ 2 + b _ i P _ i + c _ i$$

یا

$$\large \frac { \partial F _ i } { \partial P _ i } = 2 a _ i P _ i + b _ i$$

حال، با توجه به معادله (۲۰)، داریم:

$$\large \lambda = P _ {\text{f} i } \frac {\partial F _ i } { \partial P _ i } = P _ {\text{f} i } ( 2 a _ i P _ i + b _ i ) \;\;\;\;\; ( 2 7 )$$

که در آن،

$$\large P _ { \mathrm { f i } } = \frac { 1 } { 1 - \frac { \partial P _ { \mathrm { l o s } } } { \partial P _ { i } } } = \frac { 1} { 1 - 2 \sum _ { j = 1} ^ { N } B _ { i j } P _ { j } - B _ { i 0 } } \;\;\;\;\; (28)$$

فلوچارت حل مسئله پخش بار اقتصادی در شکل زیر نشان داده شده است.

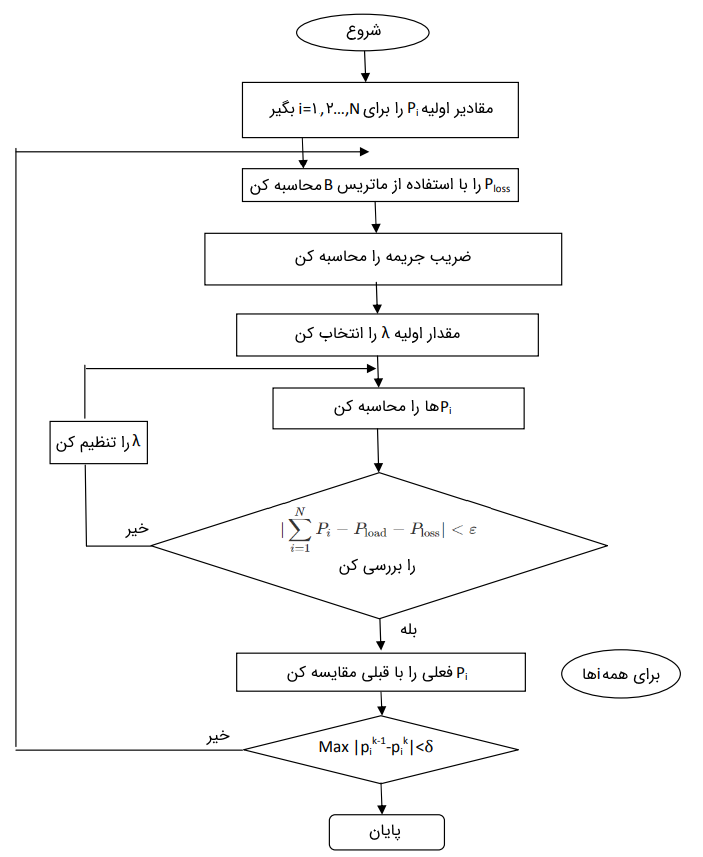
پخش بار اقتصادی با استفاده از روش‌های بهینه‌سازی

پخش بار اقتصادی اساساً یک مسئله بهینه‌سازی هزینه است. می‌توان از روش‌های بهینه‌سازی، مانند برنامه‌ریزی خطی، برنامه‌ریزی درجه دوم، روش‌های ابتکاری (مانند الگوریتم ژنتیک)، برنامه‌ریزی پویا و... برای حل مسئله پخش بار استفاده کرد. در اینجا، حل مسئله پخش بار را با استفاده از برنامه‌ریزی خطی به طور خلاصه بیان می‌کنیم.

پخش بار اقتصادی با استفاده از برنامه‌ریزی خطی

تابع هزینه درجه دوم ژنراتورها را می‌توان به صورت زیر خطی کرد:

$$\large \begin {aligned} F _ { i } \left ( P _ { i } \right ) & \approx F _ { i } \left ( P _ { i }^ { ( 0 ) } \right ) + \left . \frac { \partial F _ { i } \left ( P _ { i } \right ) } { \partial P _ { i } } \right | _ { P _{ i } ^{ ( 0 ) }} \Delta P _ { i } \\ & = b \Delta P _ { i } + c \end {aligned} \;\;\;\;\; ( 29 )$$

که در آن، $$b = \left . \frac { \partial F _ { i } \left ( P _ { i } \right ) } { \partial P _ { i } } \right | _ { P _{ i } ^{ ( 0 ) }}$$ (برای تغییرات کوچک توان، ثابت فرض شده است) و $$c = F _ i ( P _ i ^{(0)} )$$.

قید تساوی به صورت زیر است:

$$\large \phi = P _ \text{load} + P _ \text{loss} - \sum _ { i = 1 } ^ { N} P _ i = 0$$

در نتیجه، داریم:

$$\large \Delta \phi = \sum _ { i = 1 } ^ { N } \frac { \partial \phi } { \partial P _ { i } } \Delta P _ { i } = \left . \sum _ { i = 1 } ^ { N } \left ( \frac { \partial P _ { \text {loss } } } { \partial P _ { i } } - 1 \right ) \right | _ { P _ { i } ^ { (0 ) } } \Delta P _ { i } = 0$$

یا

$$\large \left . \sum _ { i = 1 } ^ { N } \left ( \frac { \partial P _ { \text {loss } } } { \partial P _ { i } } - 1 \right ) \right | _ { P _ { i } ^ { ( 0 ) } } \Delta P _ { i } = 0 \;\;\;\;\; (30)$$

معادلات (۲۹) و (۳۰) را می‌توان با استفاده از برنامه‌ریزی خطی حل کرد. الگوریتم پایه برنامه‌ریزی خطی به صورت زیر است.

الگوریتم پخش بار اقتصادی با استفاده از برنامه‌ریزی خطی

گام ۱: مجموعه متغیرهای کنترل ورودی را انتخاب کنید.

گام ۲: مسئله پخش بار را برای به دست آوردن یک جواب ممکن برای قید تعادل توان حل کنید.

گام ۳: تابع هدف را خطی کنید و مسئله برنامه‌ریزی خطی را فرمول‌بندی کنید.

گام ۴: مسئله برنامه‌ریزی خطی را حل کنید و متغیرهای کنترل اضافی بهینه را به دست آورید: $$P_ i$$.

گام ۵: متغیرهای کنترل را به‌روز کنید: $$P _ i ^{K+1} = P _ i ^ K + \Delta P _ i$$.

گام ۶: جواب پخش بار را به دست آورید و متغیرهای کنترل را به‌روز کنید.

گام ۷: اگر $$\Delta P \le \delta , \forall i = 1 , 2 , \ldots , N$$، آنگاه عملیات را متوقف کنید، در غیر این صورت به گام ۳ بروید.

فیلم آموزش پخش بار اقتصادی (دیسپاچینگ اقتصادی) در GAMS

برای آشنایی بیشتر با پخش بار اقتصادی و حل آن در نرم‌افزار گمز (GAMS)، می‌توانید به آموزش ویدئویی «آموزش پخش بار اقتصادی (دیسپاچینگ اقتصادی) در GAMS» مراجعه کنید. در درس اول این آموزشِ ۱ ساعت و ۳۲ دقیقه‌ای، قابلیت‌های نرم‌افزار GAMS و محیط و دستورات آن معرفی شده است. در درس دوم، مفاهیم مسئله پخش بار اقتصادی مقید و مدل‌سازی آن بیان شده است. شبیه‌سازی مفاهیم پخش بار اقتصادی در نرم‌افزار GAMS، موضوع درس سوم این آموزش ویدیویی است. در درس چهارم، یک شبکه نمونه در نرم‌افزار GAMS پیاده‌سازی شده است. در نهایت، در درس پنجم، نتایج به دست آمده و مورد بررسی قرار گرفته‌اند.

• برای دیدن فیلم آموزش حل مساله پخش بار اقتصادی (دیسپاچینگ اقتصادی) در GAMS (گمز) – مقدماتی + اینجا کلیک کنید.
• برای دیدن فیلم آموزش آموزش نرم افزار گمز (GAMS) + اینجا کلیک کنید.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی قدرت
• آموزش بررسی سیستم های قدرت 1
• مجموعه آموزش‌های مهندسی برق
• آموزش مبانی بهره برداری از سیستم های قدرت
• پایداری سیگنال بزرگ سیستم قدرت — به زبان ساده
• پخش بار نیوتن رافسون در متلب — از صفر تا صد
• مدل ژنراتور سنکرون — از صفر تا صد

^^