مدل ژنراتور سنکرون — از صفر تا صد

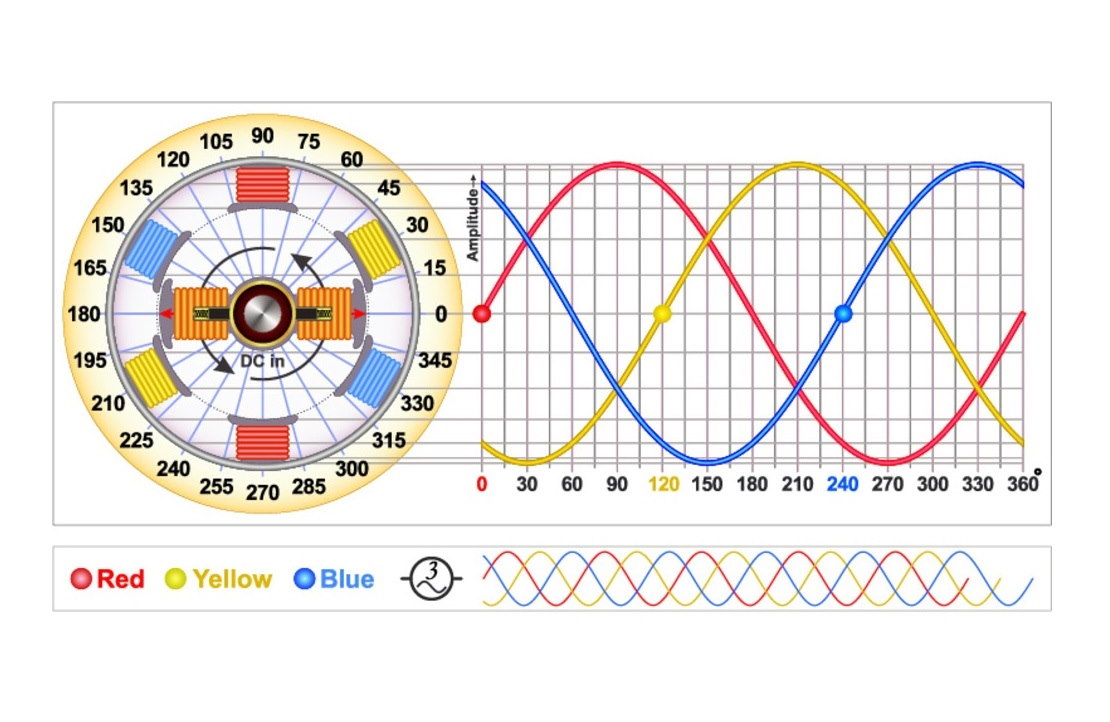
در این آموزش، نحوه به دست آوردن مدل ژنراتور سنکرون را بیان می‌کنیم. در یک ژنراتور با روتور نوع قطب صاف یا استوانه‌ای، مدل حالت مانا را می‌توان با یک منبع ولتاژ سری با راکتانس سنکرون نمایش داد. در یک ژنراتور با روتور قطب برجسته، ارائه یک مدار ساده ممکن نیست. در عوض، از نمودار فازوری برای نمایش رابطه بین ولتاژ‌ ترمینال، ولتاژ و جریان داخلی استفاده می‌شود.

دینامیک‌های الکترومغناطیسی یک ژنراتور سنکرون به ولتاژ و شار پیوندی یک مدار مربوط می‌شوند که می‌توان آن را با قانون فارادی بیان کرد. مدل‌های دینامیکی یک ژنراتور سنکرون در قاب مرجع روتور یا قاب مرجع $$dq$$ بیان می‌شوند. این قاب مرجع در حالت مانا در سرعت نامی می‌چرخد. مدل‌سازی یک ژنراتور سنکرون در قاب مرجع $$dq$$ یک تکنیک بسیار مهم است. تبدیل متغیرهای مختلف از قاب $$abc$$ به قاب $$dq$$ به عنوان تبدیل پارک شناخته می‌شود. مقاله پارک در سال ۱۹۲۹ به عنوان دومین مقاله تأثیرگذار مهندسی قدرت در قرن بیستم شناخته شد. اولین مقاله تأثیرگذار در این زمینه را فورتسکیو در در سال ۱۹۱۸ درباره نظریه مؤلفه‌های متقارن ارائه کرد.

تبدیل پارک در تحلیل ماشین‌های سنکرون یا آسنکرون مورد استفاده قرار می‌گیرد. در این تبدیل، متغیرهای استاتور در قاب مرجع روتور بیان می‌شوند. مزیت اصلی این کار، آن است که معادلات دیفرانسیل خطی با اندوکتانس‌های متغیر با زمان به معادلات دیفرانسیل خطی با ضرایب نامتغیر (ثابت) تبدیل می‌شوند.

تبدیل پارک در متون کلاسیک، مثلاً کتاب برگن و ویتال، و کراوس، مبتنی بر ماتریس تبدیل $$\mathbf{P}$$ در دامنه حقیقی است ($$ \mathbf {i} _ {dq0} = \mathbf {Pi}_{abc}$$). در این آموزش، مفهوم بردار فضایی را نیز معرفی کرده و آن را به تبدیل قاب مرجع اعمال می‌کنیم. معرفی مفهوم بردار فضایی منجر به یک روال سرراست در استخراج مدل حالت مانا و دینامیکی خواهد شد.

مدل ژنراتور سنکرون در حالت مانا

مدل مداری حالت مانای یک ژنراتور براساس اصل برهم‌نهی به دست می‌آید. ابتدا، فقط شار روتور را در نظر می‌گیریم. سپس، فقط اثر جریان استاتور را بررسی خواهیم کرد (عکس‌العمل آرمیچر). در ادامه، این دو اثر را با هم ترکیب کرده و مدل مداری، و همچنین نمودار فازوری و عبارات توان را به دست می‌آوریم.

ولتاژ داخلی ناشی از جریان تحریک روتور

برش مقطعی یک ژنراتور سنکرون دو قطب با روتور قطب برجسته در شکل ۱ نشان داده شده است.

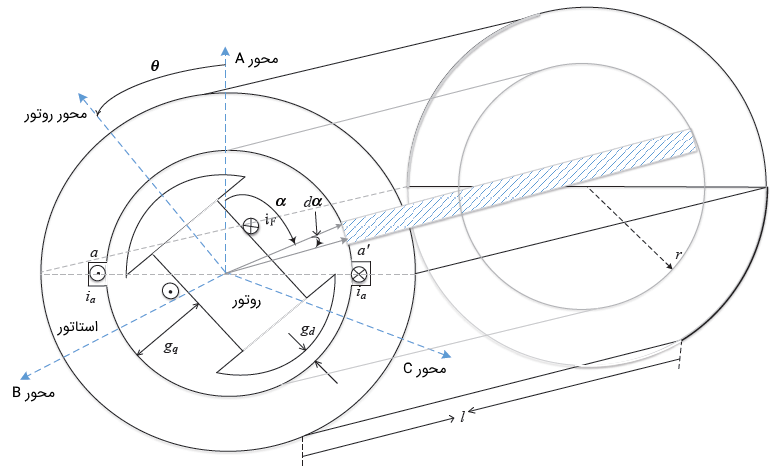
مدار روتور با ولتاژ $$v_F$$ و جریان مستقیم $$i_F$$ تحریک می‌شود. روتور با سرعت $$\omega$$ می‌چرخد. این جریان DC در طی حرکت شاری را به فرم یک شکل موج سیار در فاصله هوایی تولید می‌کند. اگر از قاون آمپر استفاده کنیم، می‌توانیم شدت میدان و چگالی شار فاصله هوایی را بیابیم.

$$ \large \oint _ {\Gamma } H d l = N _ F i _ F \;\;\;\;\; (1) $$

که در آن، $$H$$ شدت میدان مغناطیسی، $$\Gamma$$ مسیر پیوند شار، و $$ N_F$$ تعداد سیم‌پیچی‌های روتور است. نفوذپذیری مغناطیسی فاصله هوایی بسیار کمتر از مقدار آن در روتور و استاتور است. بنابراین، اگر مسیر را به دو بخش تقسیم کنیم (فاصله هوایی $$\Gamma _ 1$$ و فاصله غیرهوایی $$\Gamma _2$$)، داریم:

$$ \large \begin {align*} N_ F i _ F & = \int _ { \Gamma _ 1 } \frac { B } { \mu _ 0 } d l + \int _ { \Gamma _ 2 } \frac { B } { \mu } d l \\ & \approx
\int _ { \Gamma _ 1 } \frac { B } { \mu _ 0 } d l \;\;\;\;\;\;\;\;\;\; \text{since}\;\;\; \mu \gg \mu _ 0 \\
& = 2 g _ d \frac{B} {\mu _ 0 }
\end {align*} \;\;\;\;\; (2)$$

که در آن، $$B$$ چگالی شار، و $$g_d$$ اندازه فاصله هوایی در مسیر شار روتور است. در یک موتور قطب صاف، اندازه فاصله هوایی یکنواخت است. اما در روتور قطب برجسته، فاصله هوایی یکنواخت نیست. هرچند، حتی برای یک روتور قطب برجسته، $$g_d$$ یک فاصله ثابت است، زیرا نشان دهنده اندازه فاصله هوایی در مسیر شار روتور است.

رابطه بالا با فرض خطی بودن میدان مغناطیسی نوشته شده است. بنابراین:

$$ \large \mu H = B . \;\;\;\;\; (3) $$

اندازه چگالی شار در فاصله هوایی را می‌توان از رابطه زیر به دست آورد:

$$ \large B = \frac { \mu _ 0 } { 2 g _ d } N_ F i _F . $$

در فاصله هوایی، چگالی شار یکسان خواهد بود و جهت یکسانی دارد (در روتور از $$\frac {- \pi}{2}$$ تا $$\frac{\pi}{2}$$ برقرار است و با توجه به موقعیت روتور، از آن خارج می‌شود. در $$\pi $$ باقیمانده (خارج از بازه $$-\pi / 2 $$ تا $$\pi /2$$) نیز شار به روتور وارد می‌شود). جهت خروج شار را به عنوان جهت مثبت، و ورود آن به روتور را به عنوان جهت منفی در نظر می‌گیریم.

دامنه شکل موج پایه (اساسی) مربوط به یک شکل موج مربعی با اندازه ۱ برابر با $$\frac{4}{\pi}$$ است (شکل ۲ را ببینید). بنابراین، دامنه مؤلفه اساسی چگالی شار به صورت زیر است:

$$ \large \hat { B} = \frac { 4 } { \pi} \frac { \mu _ 0 } { 2 g _ d } N_ F i _ F . \;\;\;\;\; (4)$$

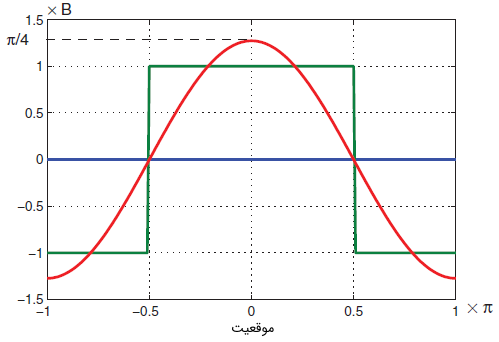
اکنون فرض دوم را در نظر می‌گیریم. ماشین‌ها به گونه‌ای طراحی شده‌اند که یک توزیع شار سینوسی در فاصله هوایی داشته باشند. بنابراین، در فاصله هوایی، در موقعیت تصادفی که با زاویه $$ \alpha$$ از محور مرجع نشان داده می‌شود، چگالی شار به صورت زیر بیان می‌شود:

$$ \large B _ F ( \alpha ) = \hat { B} \cos ( \alpha - \theta ) = \frac { 4 } { \pi} \frac {\mu _ 0 } {2 g _ d } N_ F i _F \cos ( \alpha - \theta ) \;\;\;\;\; (5)$$

که در آن، $$\theta$$ موقعیت شار یا موقعیت روتور است. پایین‌نویس $$F$$ برای نشان دادن شار روتور استفاده می‌شود، زیرا در بخش‌های بعدی شارهای دیگری نیز معرفی خواهد شد.

اکنون سیم‌پیچ فاز $$A$$ را در نظر می‌گیریم و شار پیوندی $$ \lambda _ {aa^\prime}$$ را برای شار $$ B_F$$ روتور محاسبه می‌کنیم. برای یافتن $$ \lambda _ {aa ^ \prime}$$، باید کل شاری را که با سیم‌پیچ $$aa ^\prime $$ در فضای گاوسی فاصله هوایی احاطه می‌شود محاسبه کنیم. از آنجایی که چگالی در مکان‌های مختلف متفات است، از انتگرال‌گیری استفاده می‌کنیم.

ابتدا، یک بخش از سطح گاوسی را در نظر می‌گیریم که متناسب با زاویه کوچک $$d \alpha $$ است. مساحت این سطح $$ r l d \alpha $$ است. چگالی شار متناظر نیز $$ \hat{B} \cos ( \alpha - \theta ) $$ است. در ادامه، انتگرال را از $$-\pi / 2 $$ تا $$ \pi / 2 $$ محاسبه می‌کنیم.

$$ \large \begin {align*}
\phi _ {a a^ \prime } & = \int _ {-\pi / 2 } ^ {\pi / 2} {\hat {B} \cos (\alpha - \theta ) } r l d \alpha \\
& = 2 r l \hat{B} \cos \theta
\end {align*} \;\;\;\;\; ( 6 ) $$

شار پیوندی در $$aa^\prime$$، برابر با $$ N \phi _{aa^ \prime } $$ با $$N$$ به عنوان تعداد سیم‌پیچ‌های فاز $$a$$ است.

$$ \large \begin {align*}
\lambda _{aa^ \prime} & = 2 Nrl \hat { B } \cos \theta \\
& = \underbrace { 2 N r l \frac { 4 } { \pi } \frac { \mu _ 0 } { 2 g _ d } N_F} _ { M _ F } i _F \cos \theta = M_F i _F \cos \theta
\end {align*} \;\;\;\;\; ( 7 ) $$

که در آن، $$M_F$$ اندوکتانس متقابل نامیده می‌شود.

به طور مشابه، اگر بخواهیم شارهای پیوندی سیم‌پیچ‌های $$bb^\prime$$ و $$ c c ^ \prime$$ را پیدا کنیم، انتگرال‌گیری باید در بازه $$ \left [ \frac {2 \pi }{3} - \frac {\pi}{2} , \frac{2 \pi } { 3 } + \frac{\pi}{2} \ \right ] $$، و $$ \left [ \frac {4 \pi }{3} - \frac {\pi}{2} , \frac{4 \pi } { 3 } + \frac{\pi}{2} \ \right ] $$ براساس توزیع سیم‌پیچ‌های استاتور باشد. توجه کنید که سیم‌پیچ‌های استاتور به گونه‌ای توزیع شده‌اند که محور مرجع فاز $$bb^ \prime$$ به اندازه ۱۲۰ درجه از $$aa^\prime$$ جلوتر باشد. فاز $$cc^ \prime$$ نیز به اندازه ۱۲۰ درجه جلوتر از فاز $$bb^\prime $$ است.

$$ \large \begin {align*}
\lambda _ {b b^ \prime } & = N \int _ {\frac{2\pi}{3} -\frac{\pi}{2}} ^ {\frac{2\pi}{3} + \frac{\pi}{2}} \hat {B} \cos (\alpha - \theta ) r l d \alpha \\
& = 2 N r l \hat {B} \cos \left ( \theta - \frac{2 \pi}{3} \right )
\end {align*} \;\;\;\;\; ( 8 ) $$

$$ \large \begin {align*}
\lambda _ { c c ^ \prime } & = N \int _ {\frac{ 4 \pi } { 3 } -\frac{\pi}{2}} ^ {\frac{ 4 \pi}{3} + \frac{\pi}{2}} \hat {B} \cos (\alpha - \theta ) r l d \alpha \\
& = 2 N r l \hat {B} \cos \left ( \theta + \frac{2 \pi}{3} \right )
\end {align*} \;\;\;\;\; ( 9 ) $$

طبق قانون فارادی، پیوستگی شار یک EMF یا ولتاژ را القا می‌کند، مثلاً $$ e _ {a^\prime a } = \frac { d \lambda _{aa^\prime}}{dt}$$. علاوه بر این، به جای استفاده از $$e_{a^\prime a}$$، از $$e_{aa^\prime}$$ استفاده خواهیم کرد، زیرا ولتاژ‌ ژنراتور مانند منبع ولتاژ‌ی است که جریان از آن خارج می‌شود. بنابراین، داریم:

$$ \large e _ {a a ^ \prime } = - \frac {d \lambda _ { aa^\prime } } { d t } = \dot { \theta } M _ F i _F \sin \theta = \omega M_F i _F \cos \left ( \theta - \frac{\pi}{2} \right ) . \;\;\;\;\; ( 1 0 ) $$

با در نظر گرفتن شرایط نامی، وقتی که سرعت نامی $$\omega _ 0$$، و $$\theta = \omega _ 0 t+ \theta _ 0 $$ است، ولتاژ‌ داخلی $$ e _ {aa^\prime}$$ را داریم و فازور متناظر با آن، $$\bar {E_a}$$ است:

$$ \large \begin {align*}
e _ { a a ^ \prime } & = -\frac { d \lambda _ {a a^\prime } } { dt } = \dot { \theta } M_F i _F \sin \theta = \omega M_F i _F \cos \left ( \omega _ 0 t + \theta _ 0 - \frac {\pi} { 2 } \right ) ,
\\ \bar { E _ a } & = \frac { \omega M_F i _F} {\sqrt{2}} e ^ {j (\theta _ 0 - \frac{\pi}{2})} .
\end {align*} \;\;\;\;\; ( 11 ) $$

با تعریف $$ \delta = \theta _ 0 - \frac{\pi}{2}$$، داریم:

$$ \large \bar { E _ a } = \frac { \omega M_F i _F } { \sqrt { 2 }} e ^ { j \delta} \;\;\;\;\; ( 12 ) $$

$$ \theta _ 0$$ موقعیت اولیه محور روتور (محور $$d$$) نسبت به محور مرجع (استاتیک یا ایستا) و $$ \delta$$ موقعیت اولیه محور قائم (محور $$q$$) نسبت به محور مرجع است.

عکس‌العمل آرمیچر یک ژنراتور قطب صاف

در این بخش، شار روتور در نظر گرفته نمی‌شود. فقط جریان‌های سه فاز $$i_a$$، $$i_b$$ و $$i_c$$ و اثر ترکیب آن‌ها را در تولید یک شار و EMF نشان می‌دهد. جریان‌ها سه فاز متعادل هستند.

$$ \large \begin {align*}
i _ a & = I _ m \cos ( \theta _ a ) \\
i _ b & = I _ m \cos \left ( \theta _ a - \frac {2 \pi } {3} \right ) \\ i _ c & = I _ m \cos \left ( \theta _ a + \frac {2 \pi } {3} \right )
\end {align*} \;\;\;\;\; ( 13) $$

فرض می‌کنیم فاصله هوایی یکنواخت باشد. برای جریان $$ i _ a$$ مربوط به فاز $$a$$، با استفاده از تکنیک مشابه به کار رفته در محاسبات چگالی شار ناشی از جریان $$i_F$$ روتور، می‌توانیم چگالی شار را در هر نقطه از فاصله هوایی محاسبه کنیم. علاوه بر این، می‌توانیم عبارت چگالی شار را برای $$i_b$$ و $$i_c$$ نیز بنویسیم.

$$ \large \begin {align*}
B_ a (\alpha) & = \frac {4 } {\pi} \frac{ \mu _ 0} { 2 g } N i _ a \cos ( \alpha ) \\
B_ b (\alpha) & = \frac {4 } {\pi} \frac{ \mu _ 0} { 2 g } N i _ b \cos \left ( \alpha - \frac {2 \pi } {3} \right )
\\ B_ c (\alpha) & = \frac {4 } {\pi} \frac{ \mu _ 0} { 2 g } N i _ c \cos \left ( \alpha + \frac {2 \pi } {3} \right )
\end {align*} \;\;\;\;\; ( 14) $$

که در آن‌ها، $$ \alpha$$ مکانی در فاصله هوایی نسبت به محور مرجع $$a$$ است.

عبارت بالا نشان می‌دهد که در فاصله هوایی، $$B_a$$ در درجه صفر (محور $$a$$) مینیمم یا ماکزیمم خواهد بود، در حالی که $$B_b$$ در زاویه ۱۲۰ درجه (محور $$b$$) و $$B_c$$ در زاویه ۱۲۰- درجه (محور $$c$$)، ماکزیمم یا مینیمم است. جریان‌ها متغیر با زمان هستند. بنابراین، اندازه چگالی شار نیز با زمان تغییر می‌کند. چگالی شار ترکیب شده، برابر است با:

$$ \large \begin {align*}
B _ {ar} ( \alpha ) & = B_ a (\alpha) +B_ b (\alpha) +B_ c ( \alpha ) \\
& = \frac {4 } {\pi} \frac{ \mu _ 0} { 2 g } N I_m \left ( \cos \theta _ a \cos \alpha + \cos \left ( \theta _ a - \frac{2 \pi}{3} \right ) \cos \left ( \alpha - \frac {2 \pi} { 3 } \right ) \\
+ \cos \left ( \theta _a + \frac {2 \pi }{3} \right ) \cos \left ( \alpha + \frac {2 \pi }{3} \right ) \right )
\\ & = \frac {4 } {\pi} \frac{ \mu _ 0} { 2 g } N \frac {3 } {2}I_m \cos ( \alpha - \theta _ a )
\end {align*} \;\;\;\;\; ( 1 5 ) $$

پایین‌نویس $$ar$$ واکنش آرمیچر را نشان می‌دهد.

اگر این عبارت را با چگالی شار تولیدی ناشی از $$i_F$$ مقایسه کنیم، آن را به صورت زیر نمایش می‌دهیم:

$$ \large B _ F ( \alpha ) = \frac { 4 } { \pi} \frac { \mu _ 0 } {2 g _d } N_ F i _F \cos (\alpha - \theta ) \; \; \; \; \; ( 1 6 ) $$

در می‌یابیم که اثر جریان‌های سه فاز متعادل $$(i_a, i_b, i_c)$$ در یک فاصله هوایی یک ژنراتور قطب صاف، مانند یک جریان DC روتور با اندازه $$\frac{3}{2} I_m$$ با یک سرعت چرخشی مشابه فرکانس الکتریکی است.

تذکر: میدان مغناطیسی گردان مهم‌ترین مفهوم در ماشین ac است. این میدان را می‌توان با یک جریان روتور DC یا جریان‌های سه فاز متعادل استاتور تشکیل داد.

برای $$B_{ar}$$، با استفاده از تکنیک مشابه بخش قبل برای یافتن شار پیوندی با سیم‌پیچ استاتور $$aa^\prime $$، داریم:

$$ \large \begin {align*}
\lambda _{a r } & = \underbrace { 2 N r l \frac { 4 } { \pi } \frac { \mu _ 0 } { 2 g _ d } N \frac {3}{2}} _ { L_{s1} } I _ m \cos ( \theta _ a ) \\
& = L_{s1} i _ a
\end {align*} \;\;\;\;\; ( 17 ) $$

EMF القایی $$ v _{ar}$$ را می‌توان به صورت زیر بیان کرد:

$$ \large v _ {ar} = - \frac {d \lambda _ {ar}} { d t } = - L _ {s1} \frac { d i _a}{d t} . \;\;\;\;\; (18)$$

مدار، نمودار فازوری، توان و گشتاور ژنراتور قطب صاف

با اضافه کردن شار روتور و واکنش آرمیچر با یکدیگر، می‌توانیم کل پیوستگی شار را که به $$aa^\prime$$ لینک می‌بندد در اثر شار فاصله هوایی بیابیم:

$$ \large \begin {align*}
\lambda _{a g } = \underbrace { M_F i _ F \cos \theta } _ { \lambda _ {a a ^ \prime}} + \underbrace { L _ {s1} i _a } _ {\lambda _ {ar}}. \end {align*} \;\;\;\;\; ( 1 9 ) $$

که در آن، $$\lambda _{aa^\prime}$$ پیوستگی شار ناشی از جریان روتور و $$ \lambda _ {ar}$$ پیوستگی شار ناشی از جریان‌های استاتور یا واکنش آرمیچر است.

ولتاژ $$v_{ag}$$ فاصله هوایی متناظر به صورت زیر است:

$$ \large v _ {a g} = - \frac { d \lambda _ {ag}} { d t } = \omega M_F i _F \sin \theta - L_{s1} \frac { d i _a}{d t} \;\;\;\;\; (20)$$

اگر عبارات شرایط حالت مانا و شرایط نامی را در نظر بگیریم، آنگاه پیوستگی‌های شار به صورت زیر بیان می‌شوند:

$$ \large \begin {align*}
\lambda _ {a a ^ \prime } ( t ) & = M _ F i _ F \cos ( \omega _ 0 t + \delta + \pi / 2 ) \\
\lambda _ {ar} ( t ) & = L _ {s1} I _ m \cos ( \omega _ 0 t + \theta _ {a 0 } ) \\
\lambda _ {ag} (t) & = \lambda _{aa} (t) + \lambda _ {ar} (t)
\end {align*} \;\;\;\;\; ( 21) $$

ولتاژ‌ القایی توسط کل پیوستگی شار فاصله هوایی به صورت زیر است:

$$ \large \begin {aligned} v _ { a g } ( t ) & = \omega _ { 0 } M _ { F } i _ { F } \sin \theta + \omega _ { 0 } L _ { s 1 } I _ { m } \sin \theta _ { a } \\ & = \omega _ { 0 } M _ { F } i _ { F } \sin \left ( \omega _ { 0 } t + \theta _ { 0 } \right ) + \omega _ { 0 } L _ { s 1 } I _ { m } \sin \left ( \omega _ { 0 } t + \theta _ { a 0 } \right) \\ & = \omega _ { 0 } M _ { F } i _ { F } \cos \left ( \omega _ { 0 } t + \theta _ { 0 } - \pi / 2 \right ) + \omega _ { 0 } L _ { s 1 } I _ { m } \cos \left ( \omega _ { 0 } t + \theta _ { a 0 } - \pi / 2 \right ) \end {aligned} \;\;\;\;\; (22)$$

واکنش آرمیچر برای پیوستگی شار به صورت زیر بیان می‌شود:

$$ \large \begin {align*}
\bar { \lambda _ { a g } } & = \bar { \lambda _ { a a ^ \prime } } + \bar { \lambda _ { a r } } = \frac { M _ F i _ F} { \sqrt { 2 } } e ^ { j (\delta + \pi / 2)} + L _ { s 1} \bar { I _ a } \\
& = j \frac {\bar { E_ a } } { \omega _ 0 } + L _{s1} \bar { I _ a } .
\end {align*} \;\;\;\;\; ( 23) $$

رابطه فازور برای ولتاژ و جریان‌ها به صورت زیر است:

$$ \large
\begin {aligned} \bar { V } _ { a g } & = \frac { \omega _ { 0 } M _ { F } i _ { F } } { \sqrt { 2 } } e ^ { j \left ( \theta _ { 0 } - \pi / 2 \right ) } + X _ { s 1 } \frac { I _ { m } } { \sqrt { 2 } } e ^ { j \left ( \theta _ { a } - \pi / 2 \right ) } \\ & = E _ { a } e ^ { j \delta } - j X _ { s 1 } \frac { I _ { m } } { \sqrt { 2 } } e ^ { j \theta _ { a } } \\ & = \bar { E } _ { a } - j X _ { s 1 } \bar { I } _ { a } \end {aligned}
\;\;\;\;\; ( 2 4 ) $$

که در آن، $$X_ {s1} = \omega _ 0  L_{s1}$$.

اگر مقاومت استاتور و مقاومت نشتی را در نظر بگیریم، آنگاه عبارت زیر را داریم:

$$ \large \bar {E } _ a = \bar {V } _ a + ( r + j X _ {ls} + j X _ {s 1} ) \bar{I}_a = \bar{V}_a + ( r + j X_s ) \bar{I}_a \;\;\;\;\; (25)$$

که در آن، $$ X_ s $$ راکتانس سنکرون نامیده می‌شود.

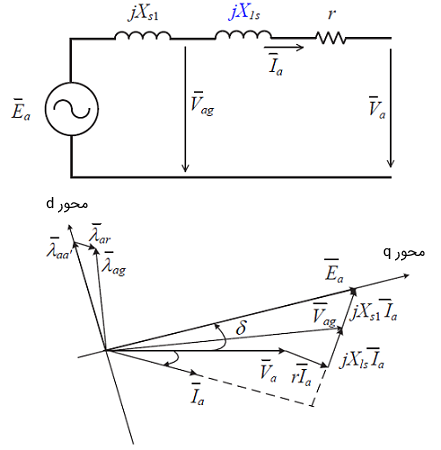
مدل مداری و نمودار فازوری یک ژنراتور قطب صاف در شکل ۳ نشان داده شده است. اکنون محورهای $$dq$$ را معرفی می‌کنیم. محور روتور، محور مستقیم یا محور $$d$$ نامیده می‌شود که در شکل ۱ نشان داده شد. محور قائم یا محور $$q$$ به اندازه ۹۰ درجه عقب‌تر از محور $$d$$ است. در نمودار فازوری نیز از محور $$q$$ برای مشخص کردن جهت ولتاژ داخلی، و از محور $$d$$ برای مشخص کردن جهت فازور شار روتور استفاده می‌کنیم.

با داشتن فازورهای ولتاژ و جریان ترمینال، می‌توانیم ولتاژ داخلی $$E_a$$ و زاویه فاز $$\delta$$ آن را پیدا کنیم. توان اکتیو تحویلی ژنراتور را می‌توان به سادگی با چشم‌پوشی از $$r$$ پیدا کنید.

$$ \large P_ a = \frac { E _ a V _a } { X _s } \sin \delta \;\;\;\;\; (26)$$

اگر فرض کنیم که زاویه فاز ولتاژ ترمینال صفر است $$ v _a (t ) = \sqrt {2} V_a \cos (\omega _ 0 t)$$. $$\delta$$ اختلاف زاویه بین دو فازور ولتاژ $$ \bar{E}_a$$ و $$ \bar{V}_a$$ است.

مثال قانون لنز

قانون لنز بیان می‌کند که اگر یک شار اصلی، EMF را القا کند و این EMF سبب تولید جریان شود، آنگاه این جریان، شاری را تولید می‌کند که شار اصلی را ضعیف خواهد کرد.

وقتی یک شین ترمینال ژنراتور اتصال کوتاه شود، اگر از مقاومت چشم‌پوشی کنیم، فازور جریان، فازور شار آرمیچر، و فازور شار روتور را هم نسبت به محور $$q$$ خواهیم داشت:

$$ \large \bar {E} _ a = E _a, \;\;\;\;\; (27)$$

$$ \large \bar {\lambda} _ { aa^\prime } = j \frac {E_a} {\omega}, \;\;\;\;\; (28) $$

$$ \large \bar {I _a } = \frac {E_a} {j X _ s} = - j \frac {E_a} { X _s}, \;\;\;\;\; (29) $$

$$ \large \bar {\lambda } _{ar} = L_s \bar {I_a} = - j L_s \frac {E_a} { X _s} = - j \frac { E _ a } { \omega }. \;\;\;\;\; (30) $$

بنابراین، شار آرمیچر شار روتور را حذف می‌کند و شار خالص فاصله هوایی صفر است.

مفهوم بردار فضایی

در این بخش، مفهوم بردار فضایی را بیان می‌کنیم که کاربرد گسترده‌ای در ماشین‌های ac و الکترونیک قدرت دارد.

همان‌طور که احتمالاً پی برده‌اید، این مفهوم از میدان مغناطیسی گردان آمده است. براساس تحلیلی که در بخش قبل ارائه کردیم، دو یافته مهم داریم:

1. یک نیروی محرکه مغناطیسی (MMF) گردان و همچنین یک میدان مغناطیسی گردان، ناشی از جریان تحریک DC ثابت $$i_F$$ روی روتور تشکیل می‌شوند. این جریان ثابت یک میدان مغناطیسی سینوسی با اندازه ثابت در فاصله هوایی تولید خواهد کرد. علاوه بر این، روتور با سرعت $$\omega$$ می‌چرخد. بنابراین، این میدان مغناطیسی گردان است، یا یک میدان مغناطیسی گردان با اندازه ثابت است.
2. جریان‌های سه فاز متعادل استاتور نیز یک MMF گردان و همچنین یک میدان مغناطیسی گردان شکل می‌دهند. اگر فرکانس الکتریکی $$\omega$$ باشد، میدان مغناطیسی گردان با سرعت $$\omega $$ در حال چرخش است.

بررسی فیزیک MMF: در هر موقعیت از فاصله هوایی (که به عنوان زاویه $$ \alpha$$ از محور مرجع نمایش داده می‌شوند)، MMF به صورت زیر است:

$$ \large \begin{align*}
F _ a (\alpha) & = N i _ a \cos \alpha \\
F _ b (\alpha) & = N i _b \cos \left ( \alpha - \frac {2 \pi}{3} \right ) \\
F _ c (\alpha) & = N i _c \cos \left ( \alpha + \frac {2 \pi}{3} \right )
\end {align*} $$

که در آن، $$ \alpha$$ زاویه کلی در فاصله هوایی نسبت به محور $$a$$، و $$F$$ معرف MMF است.

از معادلات بالا در می‌یابیم که وقتی $$\alpha = 0$$ باشد، $$ F_a$$ ماکزیمم است. بر همین اساس، وقتی که $$ \alpha = \frac {2 \pi}{3}$$ باشد، $$F_b$$ ماکزیمم می‌شود؛ همچنین، وقتی که $$ \alpha = \frac {4 \pi}{3}$$ باشد، $$F_c$$ ماکزیمم خواهد بود. جریان‌های $$i_a$$، $$i_b$$ و $$ i _c$$ را سه فاز متعادل در نظر می‌گیریم.

$$ \large \begin {aligned} i _ { a } ( t ) & = I _ { m } \cos \theta _ { a } = I _ { m } \cos \left ( \omega _ { e } t + \theta _ { a } \right ) \\ i _ { b } ( t ) & = I _ { m } \cos \left ( \theta _ { a } - \frac { 2 \pi } { 3 } \right ) = I _ { m } \cos \left ( \omega _ { e } t + \theta _ { a } - \frac { 2 \pi }{ 3 } \right ) \\ i _ { c } ( t ) & = I _ { m } \cos \left ( \theta _ { a } + \frac { 2 \pi } { 3 } \right ) = I _ { m } \cos \left ( \omega _ { e } t + \theta _ { a } + \frac { 2 \pi } { 3 } \right ) \end {aligned} \;\;\;\;\; ( 31 ) $$

که در آن، $$\omega _ e$$ فرکانس الکتریکی را نشان می‌دهد.

در نتیجه، داریم:

$$ \large \begin {aligned} F ( \alpha , t ) & = N I _ { m } \left [ \cos \left ( \omega _ { e } t + \theta _ { a } \right ) \cos \alpha + \cos \left ( \omega _ { e } t + \theta _ { a } - \frac { 2 \pi }{ 3 } \right ) \cos \left ( \alpha - \frac { 2 \pi } { 3 } \right ) \right . \\ & \left . + \cos \left ( \omega _ { e } t + \theta _ { a } + \frac { 2 \pi } { 3 } \right ) \cos \left ( \alpha + \frac { 2 \pi } { 3 } \right ) \right ] \\ & = \frac { 3 } { 2 } N I _ { m } \cos \left ( \alpha - \omega _ { e } t - \theta _ { a } \right ) \end {aligned}
\;\;\;\;\; ( 3 2 ) $$

در MMF بالا، اگر فقط مینیمم آن را در دو بعد از فاصله هوایی در نظر بگیریم، آنگاه داریم:

$$ \large \hat {F} (t) = \frac {3}{2} N I _ m \;\;\;\;\; (33) $$

که $$ \alpha = \omega _ e t + \theta _ a $$.

اکنون یک فازور (یا یک بردار فضایی) را برای نمایش اندازه و زاویه MMF معرفی می‌کنیم:

$$ \large \overrightarrow {F} (t) = \hat{F} e ^ { j (\omega _e t + \theta _a )} = \frac {3}{2} N I_m e ^{j (\omega _ e + \theta _ a)} \;\;\;\;\; (34) $$

این بردار فضایی MMF از عبارت زیر می‌آید:

$$ \large \overrightarrow {F} (t) = \left [ e ^ { j 0 } i _a (t) + e ^ {j \frac {2 \pi} {3}} i _ b (t) + e ^ {j \frac {4 \pi} {3}} i _ c (t) \right ] \;\;\;\;\; (35) $$

بردار فضایی عمومی متغیرهای سه فاز $$f_a(t)$$، $$ f_b (t)$$ و $$ f_c (t)$$ به صورت زیر تعریف می‌شود:

$$ \large \begin {align*}
\overrightarrow { f ( t) } = \frac {2}{3} \left [ e ^ { j 0 } f _a (t) + e ^ {j \frac {2 \pi} {3}} f _ b (t) + e ^ {j \frac {4 \pi} {3}} f _ c (t) \right ]
\end {align*}
\;\;\;\;\; (36) $$

دقت کنید که از ضریب $$2/3$$ استفاده شده است.

اگر $$f_a(t)$$، $$f_b(t)$$ و $$f_c(t)$$ یک مجموعه سه فاز متعادل با دامنه $$ f_m$$ باشند، آنگاه در نهایت، داریم:

$$ \large \begin {align*}
\overrightarrow { f ( t) } & = \frac {2}{3} \left [ e ^ { j 0 } f _a (t) + e ^ {j \frac {2 \pi} {3}} f _ b (t) + e ^ {j \frac {4 \pi} {3}} f _ c (t) \right ] \\
& = f _ m e ^ {j \theta _ a}
\end {align*}
\;\;\;\;\; (37) $$

که فرم تحلیلی $$ f _ a $$ و به عبارت دیگر، بخش حقیقی بردار فضایی سیگنال فاز $$a$$ است.

توجه کنید که فرم تحلیلی یک سیگنال، یک تابع با مقدار مختلط است که مؤلفه‌های فرکانسی منفی ندارد. اگر $$ f _ a (t) = f _ m \cos ( \theta _a)$$، آنگاه تبدیل هیلبرت را می‌توان به صورت $$ f'_a(t) = f _ m \sin (\theta _a )$$ تعریف کرد. سیگنال تحلیلی به صورت زیر است:

$$ \large f _ a ( t) + j f'_a ( T) = f _ m ( \cos (\theta _ a ) + j \sin (\theta _ a )) = f_ m e ^ {j \theta _ a} . $$

مثال

جریان‌های زیر را در $$ t = t _ 1 $$ در نظر بگیرید:

$$ \large
\left\{ \begin {array} {c} { i _ { a } \left ( t _ { 1 } \right ) = 1 } \\ { i _ { b } \left ( t _ { 1 } \right ) = - 0 . 5 } \\ { i _ { c } \left ( t _ { 1 } \right ) = - 0 . 5 } \end {array} \right .
\;\;\;\;\; ( 38 ) $$

MMF فاصله هوایی را به ازای جریان‌های سه فاز استاتور در لحظه $$ t_ 1 : F (\alpha , t _ 1 )$$ به دست آورید.

حل: دو رویکرد برای حل مسئله وجود دارد:

۱) با جایگذاری $$w_e t + \theta _ a =0$$ و $$ I_m=1$$ در (۳۱) و (۳۲)، داریم: $$ F (\alpha , t_ 1)= \frac {3}{2} N \cos \alpha $$.

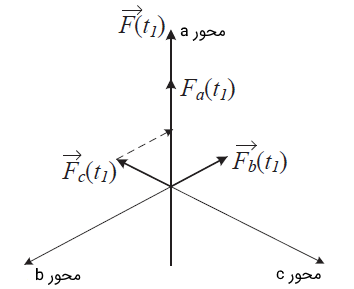
۲) رسم جواب با استفاده از نمودار فازوری شکل ۴. ابتدا $$\overrightarrow{ F } _ a ( t_ 1 )$$ را در جهت محور $$a$$ با بزرگی $$N$$ رسم می‌کنیم که در آن، $$N$$ تعداد سیم‌پیچ‌ها است. سپس، در جهت مخالف محور $$b$$، $$\overrightarrow{ F } _ b ( t_ 1 )$$ را با اندازه $$0.5 N$$ رسم می‌کنیم. در خلاف جهت محور $$c$$، بردار $$\overrightarrow{ F } _ c ( t_ 1 )$$ را با اندازه $$0.5N$$ رسم می‌کنیم. مجموع سه بردار $$1.5N$$ در جهت محور $$a$$ است. بنابراین، $$F (\alpha , t_1) = 1.5 \cos \alpha $$.

مزایای روش بردار فضایی

چرا بردار فضایی بسیار مهم است؟ با استفاده از بردارهای فضایی می‌توانیم تجزیه را انجام داده و درک بسیار بهتری نسبت به تحلیل ماشین‌هایی با روتور قطب برجسته داشته باشیم. مشابه فازورها، بردارهای فضایی شکل موج‌های سینوسی را به بردارها ترجمه و تفسیر می‌کنند. بنابراین، تجزیه بسیار آسان می‌شود.

برای مثال، می‌خواهیم MMF تشکیل شده ناشی از جریان‌های استاتور ار با دو MMF تجزیه کنیم: یکی هم‌راستا با محور $$d$$ و دیگری هم‌راستا با محور $$q$$.

ابتدا، MMF را به صورت $$\overrightarrow{ F } _ s = \frac { 3 } { 2 } N I_m e ^ { j \theta _a}$$ می‌نویسیم، موقعیت محور $$d$$، $$e ^ {j \theta}$$ بوده، و موقعیت محور $$q$$ برابر با $$ e ^ {j (\theta - \frac{\pi}{2})}$$ است.

از محور $$d$$ یا محور $$q$$ به عنوان مرجع استفاده می‌کنیم. بنابراین، باید بردار فضایی MMF را، به ترتیب، براساس محور $$d$$ یا محور $$q$$ بنویسیم.

بردار فضایی MMF به صورت زیر بیان می‌شود:

$$ \large \begin {align*}
\overrightarrow { F } _ s = \frac {3}{2} N I _ m { e ^ {j \theta _a } }
\end {align*}
\;\;\;\;\; (39) $$

اگر بردار فضایی را براساس محور $$d$$ توصیف کنیم، این بردار باید $$\overrightarrow{F}_s e ^ {-j \theta } $$ باشد:

$$ \large
\bar { F} _ { s 1 } = \frac { 3 } { 2 } N I _ { m } e ^ { j \left ( \theta _ { a } - \theta \right ) } = \underbrace { \frac { 3 } { 2 } N I _ { m } \cos \left ( \theta _ { a } -\theta \right ) } _ { F _ { s d } } + \underbrace { j \frac { 3 } { 2 } N I _ { m } \sin \left ( \theta _ { a } - \theta \right ) } _ { - F _ { s q } }
\;\;\;\;\; ( 40 ) $$

اگر توصیف براساس محور $$q$$ بیان شود، بردار فضایی MMF باید $$ \overrightarrow F _s e ^ {- j ( \theta - \pi / 2 ) } $$ باشد، زیرا موقعیت محور $$q$$ نسبت به مرجع ایستا $$ \theta - \pi / 2 $$ است.

$$ \large
\bar { F} _ { s 2 } = \frac { 3 } { 2 } N I _ { m } e ^ { j \left ( \theta _ { a } - \theta + \frac{\pi}{2}\right ) } = \underbrace {- \frac { 3 } { 2 } N I _ { m } \sin \left ( \theta _ { a } -\theta \right ) } _ { F _ { s q } } + \underbrace { j \frac { 3 } { 2 } N I _ { m } \cos \left ( \theta _ { a } - \theta \right ) } _ { F _ { s d } }
\;\;\;\;\; ( 41) $$

از نماد $$\overline{F}$$ استفاده می‌کنیم. $$\overline {F}$$ یک بردار ایستا در حالت مانا است، زیرا فرکانس الکتریکی و سرعت روتور در ژنراتور های سنکرون برابرند و علاوه بر آن،‌ در حالت مانا اندازه جریان ثابت است. $$\theta _ a - \theta $$ یک ثابت و $$ \overline {F}$$ یک بردار مختلط است. باید داشته باشیم:

$$ \large \begin {align*}
\overrightarrow F _s & = \overline F_ { s 1 } \;\;\;\;\; (42) \\
& = \overline F _ { s 2 } e ^ { j (\theta - \frac { \pi } { 2 }) } =
\underbrace {- \frac { 3 } { 2 } N I _ m \sin ( \theta _ a - \theta ) e ^ {j ( \theta - \frac { \pi}{2})}}_ { \overline F _ { s q } } + \underbrace { \frac { 3 } { 2 } N I _ m \cos ( \theta _ a - \theta ) e ^ {j \theta}}_ { \overline F _ { s d } }
\end {align*} \;\;\;\;\; (43) $$

بنابراین، نشان دادیم که یک بردار فضایی را می‌توان به سادگی به دو بردار فضایی تجزیه کرد که نسبت به هم متعامد هستند.

$$ \large \begin {align*}
\overrightarrow F _ s & = \overrightarrow F _ { d s } + \overrightarrow F _ { q s } \;\;\;\;\; (44) \\
& = ( F _ { s d } - j F _ { s q } ) e ^ { j \theta } \;\;\;\;\; (45) \\
& = ( F _ { s q } + j F _ { s d } ) e ^ { j ( \theta - \frac { \pi} { 2 } )} \;\;\;\;\; (46 )
\end {align*} $$

رابطه بین بردار فضایی، بردار مختلط، $$\Large \alpha \beta $$ و تبدیل پارک

تعریف یک بردار فضایی را می‌توان در قالب ماتریس/بردار نوشت:

$$ \large \begin {align*}
\overrightarrow { i } = \frac { 2 } { 3 } \begin {bmatrix}
e ^ {j 0 } & e ^ {j \frac { 2 \pi} { 3 } } & e ^ {- j \frac {2 \pi} { 3 } } \end {bmatrix}
\begin {bmatrix}
i _a \\ i _ b \\ i _ c
\end {bmatrix}
\end {align*} \;\;\;\;\; (47) $$

اکنون دو قاب مرجع را در نظر می‌گیریم، نخست $$ \alpha \beta $$، و دوم قاب مرجع $$d q $$. قاب $$\alpha \beta $$ یک قاب ایستا است که در آن، محور $$\beta$$ به اندازه ۹۰ درجه از محور $$\alpha $$ جلوتر است ($$\overrightarrow {i} = i _ \alpha + j i _ \beta $$). بنابراین، در قاب مرجع $$\alpha \beta$$، داریم:

$$ \large \left [ \begin {array} {c} { i _ { \alpha } } \\ { i _ { \beta } } \end {array} \right ] = \frac { 2 } { 3 } \left [ \begin {array} {ccc} { 1 } & { \cos \frac { 2 \pi } { 3 } } & { \cos \frac { 2 \pi } { 3 } } \\ { 0 } & { \sin \frac { 2 \pi } { 3 } } & { - \sin \frac { 2 \pi } { 3 } } \end {array} \right ] \left [ \begin {array}{l} { i _ { a } } \\ { i _ { b } } \\ { i_ { c } } \end {array} \right ] \;\;\;\;\; ( 48)$$

در قاب مرجع $$ dq $$، محور مرجع محور $$d $$ است. بردار فضایی $$\overrightarrow{i}$$ در قاب $$d q $$ به یک بردار جدید تبدیل می‌شود. این بردار را یک بردار مختلط می‌نامیم و آن را به صورت $$\bar{I}_ {dq} = i _d - j i _ q $$ می‌نویسیم.

$$ \large \bar { I } _ { d q } = e ^ { - j \theta }\vec { i } = \frac { 2 } { 3 } \left [ e ^ { - j \theta } \quad e ^ { - j \left ( \theta - \frac { 2 \pi } { 3 } \right ) } \quad e ^ { -j \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \right ] \left [ \begin {array} { l } { i _ { a } } \\ { i _ { b } } \\ { i _ { c } } \end {array} \right ] \;\;\;\;\; ( 49 ) $$

$$ \large \left [ \begin {array} { c } { i _ { d } } \\ { i _ { q } } \end {array} \right ] = \frac { 2 } { 3 } \left [ \begin {array}{ c c } { \cos \theta } & { \cos \left ( \theta - \frac { 2 \pi }{ 3 } \right ) } & { \cos \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \\ { \sin \theta } & { \sin \left ( \theta - \frac { 2 \pi } { 3 } \right ) } & { \sin \left ( \theta + \frac { 2 \pi }{ 3 } \right ) } \end {array} \right ] \left [ \begin {array} { l } { i _ { a } } \\ { i _ { b } } \\ { i _ { c } } \end {array} \right ] \;\;\;\;\; (50) $$

برای جریان‌های سه فاز متعادل، که جریان یک فاز به صورت $$ I _ m \cos ( \theta _ a )$$ است، می‌توانیم با استفاده از مفهوم بردار فضایی $$ i _d $$ و $$ i _ q $$ را به دست آوریم. بردار فضایی جریان $$ I _ m e ^ {j \theta _ a } $$ است. اکنون این بردار فضایی را از دیدگاه روتور بررسی می‌کنیم. موقعیت روتور $$ \theta$$ است. بنابراین، بردار مختلط در قاب $$dq$$ برابر است با:

$$ \large \overline I _ { d q } = I _ m e ^ {j \theta _ a } e ^ { - j \theta } . $$

در نتیجه، $$ i _ d $$ و $$ i _ q $$ به صورت زیر به دست خواهند آمد:

$$ \large \begin {align*}
i _ d & = I _ m \cos ( \theta - \theta _ a ) , \\
i _ q & = I _ m \sin ( \theta - \theta _ a ) .
\end {align*} \;\;\;\;\;\; ( 51) $$

$$ i _ d $$ تصویر بردار فضایی جریان روی محور $$d$$ و $$ i _ q $$ تصویر بردار فضایی روی محور $$ q $$ است.

برای تشکیل ماتریس تبدیل (۵۰) به صورت مربعی، مؤلفه دنباله صفر $$ i _ 0 = \frac { 1 } { 3 } ( i _ a + i _ b + i _ c)$$ را به آن اضافه می‌کنیم. بنابراین، متغیرهای $$ d q 0 $$ به صورت زیر با متغیرهای $$abc$$ رابطه دارند:

$$ \large \left [ \begin {array} { c } { i _ { d } } \\ { i _ { q } } \\ { i _ { 0 } } \end {array} \right ] = \underbrace { \frac { 2 } { 3 } \left [ \begin {array} { c c c } { \cos \theta } & { \cos \left ( \theta - \frac { 2 \pi } { 3 } \right ) } & { \cos \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \\ { \sin \theta } & { \sin \left ( \theta - \frac { 2 \pi } { 3 } \right ) } & { \sin \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \\ { \frac { 1 } { 2 } } & { \frac { 1 } { 2 } } & { \frac { 1 }{ 2 } } \end {array} \right ] } _ { T _ { 1 } } \left [ \begin {array} { c } { i _ { a } } \\ { i _ { b } } \\ { i _ { c } } \end {array} \right ] \;\;\;\;\; (52 ) $$

کتاب‌هایی مربوط به ماشین‌های ac، یعنی کراوس، از این تبدیل استفاده می‌کنند. برگن و ویتال از یک عامل مقیاس $$ k = \sqrt {\frac{3}{2}}$$ برای ماتریس تبدیل استفاده کرده‌اند. برای مثال، $$T_1$$ را بررسی می‌کنیم:

$$ \large T _ { 1 } T _ { 1 } ^ { T } = \frac { 4 } { 9 } \left [ \begin {array} { c c c } { \frac { 3 } { 2 } } & { 0 } & { 0 } \\ { 0 } & { \frac { 3 } { 2 } } & { 0 } \\ { 0 } & { 0 } & { \frac { 3 } { 2 } } \end {array} \right ] = \frac { 2 } { 3 } \mathbf { I } \;\;\;\;\; (53) $$

با اضافه کردن یک فاکتور مقیاس ماتریس تبدیل را به یک ماتریس متعامد (Orthogonal) یا یکانی (Unitary) تبدیل می‌کنیم:

$$ \large \underbrace {k T _ 1 } _ { T _ 2 } k T_ 1 ^ T = \mathbf { I } \;\;\;\;\; (54) $$

برگن و ویتال از $$T_ 2 $$ به عنوان ماتریس تبدیل استفاده کرده‌اند.

$$ \large \left [ \begin {array} { c } { i _ {d } ^ { \prime } } \\ { i _ { q } ^ { \prime } } \\ { i _ { 0} ^ { \prime } } \end {array} \right ] = \underbrace { \sqrt { \frac { 2 } { 3 } } \left [ \begin {array} { c c c } { \cos \theta } & { \cos \left ( \theta -\frac { 2 \pi } { 3 } \right ) } & { \cos \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \\ { \sin \theta } & { \sin \left ( \theta -\frac { 2 \pi } { 3 } \right ) } & { \sin \left ( \theta + \frac { 2 \pi } { 3 } \right ) } \\ { \frac { 1 } { 2 } } & { \frac { 1 } { 2 } } & { \frac { 1 } { 2 } } \end {array} \right ] } _ { T _ { 2 } } \left [ \begin {array} { c } { i _ { a } } \\ { i _ { b } } \\ { i _ { c } } \end {array} \right ] \;\;\;\;\; (55)$$

در اینجا متغیرها را براساس تبدیل $$T_2$$ با علامت $$^ \prime$$ می‌نویسیم. تبدیل بالا تبدیل پارک نامیده می‌شود. به طور خلاصه، متغیرهای استاتور یا بردارهای فضایی بعد از تبدیل پارک از دیدگاه روتور مشاهده می‌شوند.

$$ \large \overline I _ { d q} = e ^ {-j \theta } \overrightarrow i \;\;\;\;\; ( 56) $$

$$ \large \overline v _ { d q} = e ^ {-j \theta } \overrightarrow v \;\;\;\;\; ( 57) $$

$$ \large \overline \lambda _ { d q} = e ^ {-j \theta } \overrightarrow \lambda \;\;\;\;\; ( 58 ) $$

لازم به ذکر است که فقط جریان‌های مربوط به بردار فضایی دارای یک متناظر فیزیکی هستند که به MMF یا شار مرتبط است. بقیه مفهوم فیزیکی ندارند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی قدرت
• آموزش کنترل موتورهای الکتریکی صنعتی ۲
• مجموعه آموزش‌های مهندسی برق
• آموزش بررسی سیستم های قدرت ۱
• مدل خط سه فاز — به زبان ساده
• کو انرژی چیست؟ — از صفر تا صد
• پروفایل بار چیست؟ — به زبان ساده

^^