پخش بار گوس سایدل — به زبان ساده

پخش بار، یکی از مباحث مهم در مطالعه سیستم‌های قدرت است که در آموزش‌های پیشین مجله فرادرس، مفاهیم و معادلات مربوط به آن را معرفی کردیم. همچنین گفتیم که روش‌هایی از قبیل گوس سایدل، نیوتن رافسون قطبی، نیوتن رافسون دکارتی و پخش بار تفکیک‌شده سریع برای حل معادلات آن وجود دارد. در این آموزش، روش گوس سایدل را معرفی می‌کنیم. پیشنهاد می‌کنیم قبل خواندن روش «پخش بار گوس سایدل»، آموزش «پخش بار در سیستم قدرت — مفاهیم و معادلات» را مطالعه کنید.

قبل از آنکه درباره روش پخش بار گوس سایدل (Gauss Seidel load flow) یا GSLF بحث کنیم، ابتدا کاربرد روش گوس سایدل پایه را برای حل مجموعه معادلات جبری غیرخطی بیان می‌کنیم.

فیلم آموزش بررسی سیستم‌ های قدرت ۱ – مرور و حل سوالات آزمون های استخدامی در فرادرس

کلیک کنید

دستگاه زیر را با $$n$$ معادله در نظر بگیرید که در آن، $$n$$ متغیر مجهول $$x_1$$، $$x_2$$، $$\ldots$$ و $$x_n$$ وجود دارد:

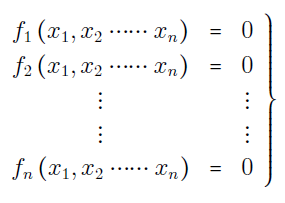
لازم به ذکر است که در معادلات (۱)،‌ توابع $$f_1$$، $$f_2$$، $$\ldots$$ و $$f_n$$ همه ذاتاً غیرخطی هستند و فرم خاصی برای آن‌ها در نظر گرفته نشده است. با عملیات جبری ساده‌ای می‌توانیم متغیر $$x_1$$ معادله اول رابطه (۱) را برحسب سایر متغیرها بنویسیم. همین کار را می‌توانیم برای سایر متغیرها انجام دهیم. با انجام این کار، معادلات (۱) به‌صورت زیر درخواهند آمد:

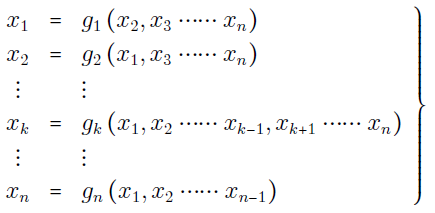
اولین گام برای محاسبه متغیرهای $$x_1$$، $$x_2$$، $$\ldots$$ و $$x_n$$ از معادلات $$g_1$$، $$g_2$$، $$\ldots$$ و $$g_n$$، درنظر گرفتن شرایط اولیه $$x_1^{(0)}$$، $$x_2^{(0)}$$، $$\ldots$$ و $$x_n^{(0)}$$ برای حل متغیرها است. با فرض این شرایط اولیه، گام‌های اصلی الگوریتم گوس سایدل به‌صورت زیر است:

گام ۱: شمارنده تکرار را $$k=1$$‌ قرار دهید.

گام ۲: متغیرها را به‌روزرسانی کنید:

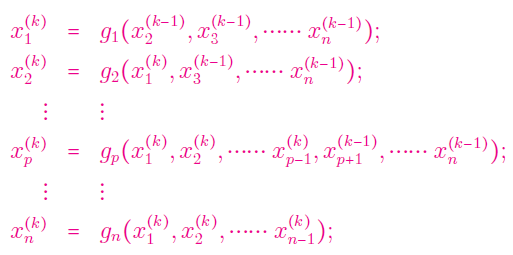
گام ۳: خطای زیر را برای همه مقادیر $$i=1, 2, \ldots , n$$ محاسبه کنید:

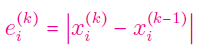
گام ۴: از بین خطاهایی که در مرحله قبل محاسبه کرده‌اید، بزرگ‌ترین مقدار را تعیین کنید:

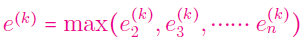
گام ۵: اگر $$e_r< \epsilon$$ ($$\epsilon$$ کران تلورانس است)، الگوریتم را متوقف کرده و پاسخ به‌دست‌آمده را یادداشت کنید. در غیر این صورت، $$k=k+1$$ قرار دهید و به گام ۲ برگردید.

لازم به ذکر است که در گام ۲، برای به‌روزرسانی متغیر $$x_p$$، از به‌روزترین مقادیر $$x_1$$، $$x_2$$، $$\ldots$$ و $$x_p$$ (که قبل از $$x_p$$ در دنباله متغیرهای پاسخ قرار دارند) استفاده می‌شود، در حالی که برای متغیرهای $$x_{p+1}$$، $$x_{p+2}$$، $$\dots$$ و $$x_n$$ (که بعد از متغیر $$x_p$$‌ قرار دارند)، مقادیر حاصل از تکرار قبل مورد استفاده قرار می‌گیرند (زیرا این متغیرها هنوز به‌روزرسانی نشده‌اند). بنابراین، در گام‌های ۳ و ۴، حداکثر خطای مطلق، اختلاف بین مقادیر تکرار فعلی و تکرار قبلی است. اگر حداکثر خطا، کم‌تر از یک مقدارِ تلورانس از پیش تعیین‌شده باشد، الگوریتم همگرا می‌شود. در غیر این صورت، باید الگوریتم را ادامه داد و متغیرها را به‌روزرسانی کرد.

اکنون که با روش گوس سایدل آشنا شده‌ایم، پخش بار گوس سایدل را توضیح می‌دهیم.

پخش بار با روش گوس سایدل

از آموزش مفاهیم اصلی و روابط پخش بار می‌دانیم که معادله اساسی پخش بار به‌صورت زیر نوشته می‌شود:

فیلم آموزش بررسی سیستم های قدرت ۱ – مرور و حل تمرین در فرادرس

کلیک کنید

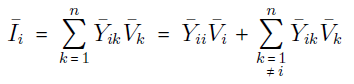
از معادله اخیر می‌توان رابطه زیر را نتیجه گرفت:

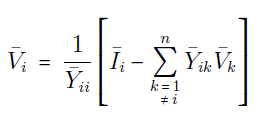
اکنون از رابطه توان زیر استفاده می‌کنیم:

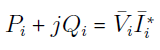
با توجه به رابطه بالا،‌ می‌توان جریان را به‌صورت زیر بیان کرد:

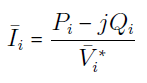
بنابراین، ولتاژ از رابطه زیر قابل محاسبه است:

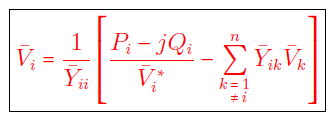
رابطه (۳)، معادله اساسی پخش بار گوس سایدل است. بدون از دست دادن کلیت مسئله، می‌توان فرض کرد $$m$$‌ ژنراتور به $$m$$ شین اول (شین ۱، شین شناور است) متصل است و سایر $$n-m$$ شین باقی‌مانده، شین بار هستند. اکنون برای درک اولیه از پخش بار گوس سایدل، فرض می‌کنیم $$m=1$$ است، یعنی تنها یک ژنراتور وجود دارد (که شین شناور نیز هست) و $$n-1$$ شین باقی‌مانده، همه شین بار هستند. برای محاسبات پخش بار، حدس اولیه ولتاژ شین‌ها ضروری است. از آن‌جایی که معمولاً انتظار می‌رود هر سیستم قدرت در شرایط حالت ماندگار عادی کار کند (با نگه داشتن ولتاژ شین‌ها بین $$0.95$$ تا $$1.05$$ پریونیت)، مقدار اولیه همه ولتاژهای مجهول شین‌ها را $$1.0 \angle 0 ^ \circ$$ پریونیت (یعنی $$\bar{V}_j^{(0)}=1.0 \angle 0^ \circ$$ برای $$j=2, 3, \ldots, n$$) فرض می‌کنیم. این فرایندِ در نظر گرفتن مقدار اولیه شین‌ها با مقدار $$1.0 \angle 0 ^ \circ$$، شروع تخت (Flat start) نامیده می‌شود. با توجه به این فرضیات، فرایند کامل پخش بار گوس سایدل (بدون شین PV) به‌صورت زیر خواهد بود:

پخش بار گوس سایدل بدون شین PV

گام ۱: شمارنده تکرار را $$k=1$$‌ قرار دهید.

فیلم آموزش دینامیک سیستم های قدرت 1 در فرادرس

کلیک کنید

گام ۲: ولتاژ شین‌ها را به‌روزرسانی کنید:

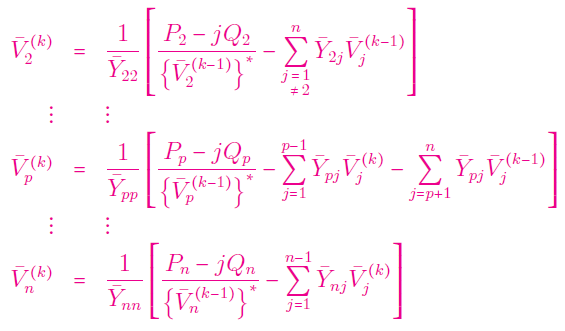
گام ۳: خطای زیر را برای همه مقادیر $$i=1, 2, \ldots , n$$ محاسبه کنید:

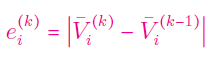
گام ۴: از بین خطاهایی که در مرحله قبل محاسبه کرده‌اید، بزرگ‌ترین مقدار را تعیین کنید:

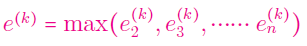
گام ۵: اگر $$e^{(k)}< \epsilon$$ ($$\epsilon$$ کران تلورانس است)، الگوریتم را متوقف کرده و پاسخ به‌دست‌آمده را یادداشت کنید. در غیر این صورت، $$k=k+1$$ قرار دهید و به گام ۲ برگردید.

اکنون که الگوریتم پخش بار گوس سایدل پایه را فرا گرفته‌ایم، می‌توانیم این الگوریتم را برای یک سیستم با چند ژنراتور بیان کنیم. قبل از آنکه درباره پخش بار گوس سایدل بحث کنیم، باید نکاتی را درباره مقداردهی اولیه ولتاژ شین‌ها بگوییم که کمی متفاوت از شروع تخت است. برای سیستمی با چند ژنراتور، مقداردهی اولیه ولتاژ شین‌ها در دو مرحله انجام می‌شود:

1. مقداردهی اولیه شین‌های بار، به‌صورت شروع تخت است که قبلاً توضیح دادیم (یعنی $$\bar{V}_j^{(0)}=1.0 \angle 0^ \circ$$ برای $$j=(m+1), (m+2), \ldots , n$$).
2. اندازه اولیه ولتاژ شین‌های PV برابر با اندازه ولتاژهای تعیین‌شده شین‌ها و زاویه اولیه آن‌ها برابر با $$0^ \circ$$ در نظر گرفته می‌شود (یعنی $$\bar{V}_j^{(0)}=V_j^{sp} \angle 0^ \circ$$ برای $$j=2, 3, \ldots ,m$$ که $$V_j^{sp}$$ اندازه ولتاژ ژنراتور $$j$$اُم است).

همان‌طور که قبلاً گفتیم، توان راکتیو مصرفی یا تولیدی یک ژنراتور ($$Q_G$$) را می‌توان با فرایند پخش بار محاسبه کرد. هرچند، هر ژنراتور محدودیت حداقل و حداکثری برای $$Q_G$$ دارد. اگر $$Q_G$$ ژنراتور در محدوده بین دو مقدار حداقل و حداکثر قرار گیرد، آن‌گاه سیستم تحریک ژنراتور قادر است ولتاژ را در مقدار مشخصی نگه دارد. اما اگر $$Q_G$$ ژنراتور به محدودیت حداقل یا حداکثر خود برسد، سیستم تحریک نمی‌تواند اندازه ولتاژ ترمینال را در مقدار معین نگه دارد. در این حالت، شین ژنراتور مانند یک شین PQ عمل خواهد کرد (P قبلاً مشخص شده و Q در مقدار حداقل یا حداکثر $$Q_G$$ در نظر گرفته می‌شود). در مهندسی برق، این پدیده (که ژنراتور مانند یک شین PQ عمل می‌کند) به‌عنوان «سوئیچ از PV به PQ» نامیده می‌شود که در محاسبات پخش بار باید آن را در نظر گرفت.

موضوع اخیر، در «الگوریتم پخش بار گوس سایدلِ کامل» گنجانده شده است که در ادامه، آن را توضیح خواهیم داد. در هر تکرار، مقدار $$Q_G$$ تزریقی هر ژنراتور محاسبه می‌شود. اگر مقدار $$Q_G$$ محاسبه‌شده بین دو محدوده بالا و پایین باشد، آن شین را هم‌چنان به‌عنوان یک شین PV در نظر می‌گیریم. در این حالت، مقدار $$|\bar{V}_i|$$ شین در مقدار تعیین‌شده باقی می‌ماند و فقط زاویه ولتاژ شین در این تکرار محاسبه می‌شود. از سوی دیگر، اگر $$Q_G$$ از محدودیت‌ها عبور کند، مقدار آن را برابر با کران (کمینه یا بیشینه) قرار داده و شین را PQ در نظر می‌گیریم. بنابراین، هم اندازه و هم زاویه شین در این تکرار محاسبه می‌شود. با توضیحاتی که بیان شد، اکنون می‌توان الگوریتم پخش بار گوس سایدل را برای سیستمی با چند ژنراتور به‌صورت زیر بیان کرد.

الگوریتم پخش بار گوس سایدل کامل

گام ۱: مقداردهی اولیه $$\bar{V}_j ^{(0)}=V_j^{sp} \angle 0^ \circ$$ را برای $$j=2, 3,  \ldots , m$$، و $$\bar{V}_j ^{(0)}=1.0 \angle 0^ \circ$$ را برای $$j=(m+1), (m+2),  \ldots , n$$ انجام دهید. شمارنده تکرار را $$k=1$$‌ قرار دهید.

فیلم آموزش بررسی سیستم‌ های قدرت ۱ – مرور و حل سوالات آزمون های استخدامی در فرادرس

کلیک کنید

گام ۲: برای $$i=2, 3, \ldots, m$$، عملیات زیر را انجام دهید:

الف) توان راکتیو را محاسبه کنید:

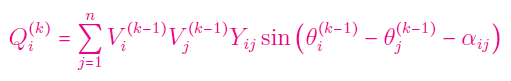
ب) اگر $$Q_i^{min} \le Q_i ^{(k)} \le Q_i ^{max}$$ برقرار باشد، مقادیر $$\left |\bar{V}_i ^{(k)} \right | = V_i ^{sp}$$ و $$\theta _i ^{(k)}= \angle \left(A_i^{(k)} \right )$$ را در نظر بگیرید.

مقدار $$A_i^{(k)}$$ از رابطه زیر قابل محاسبه است:

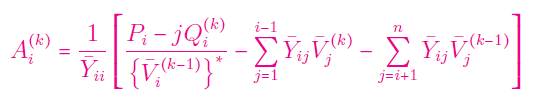
ج) اگر $$Q_i ^{(k)} \ge Q_i^{max}$$، آن‌گاه مقدار ولتاژ زیر را محاسبه کنید:

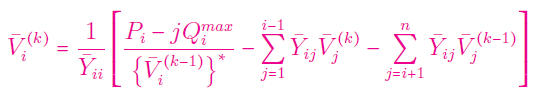
د) اگر $$Q_i ^{(k)} \le Q_i^{min}$$، آن‌گاه ولتاژ را از رابطه زیر به‌دست آورید:

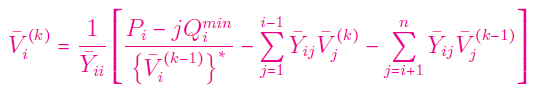
گام ۳: برای $$i=(m+1), \ldots , n$$، ولتاژ را از رابطه زیر محاسبه کنید:

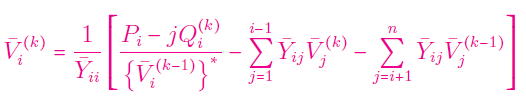
گام ۴: خطای زیر را برای همه مقادیر $$i=2, \ldots , n$$ محاسبه کنید:

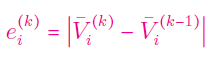
گام 5: از بین خطاهایی که در مرحله قبل محاسبه کرده‌اید، بزرگ‌ترین مقدار را پیدا کنید:

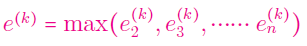
گام 6: اگر $$e^{(k)}< \epsilon$$، الگوریتم را متوقف کرده و پاسخ به‌دست‌آمده را یادداشت کنید. در غیر این صورت، $$k=k+1$$ قرار دهید و به گام ۲ برگردید.

در ادامه، مثالی را از پخش بار گوس سایدل بیان می‌کنیم.

مثال

برای درک بهتر پخش بار گوس سایدل، یک سیستم ۵ شینه را در نظر بگیرید که در شکل ۱ نشان داده شده است.

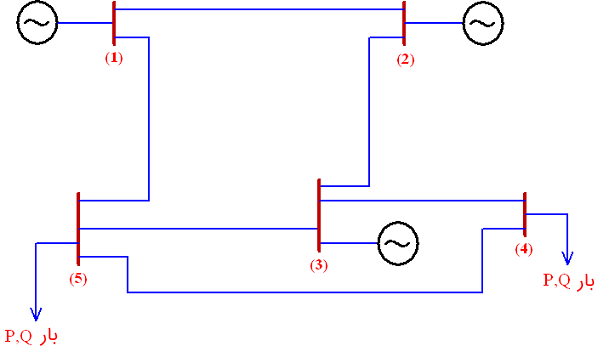
در این سیستم، ژنراتور به شین‌های ۱ تا ۳ متصل است و شین‌های ۴ و ۵، از نوع بار هستند. بنابراین، در سیستم شکل ۱، $$n=5$$ و $$m=3$$ است. علاوه بر این، شین ۱، شین شناور یا مرجع است، در نتیجه شین‌های ۲ و ۳، شین PV هستند. اطلاعات مربوط به شین‌ها و خطوط سیستم به‌ترتیب، در جدول ۱ و ۲ ارائه شده است.

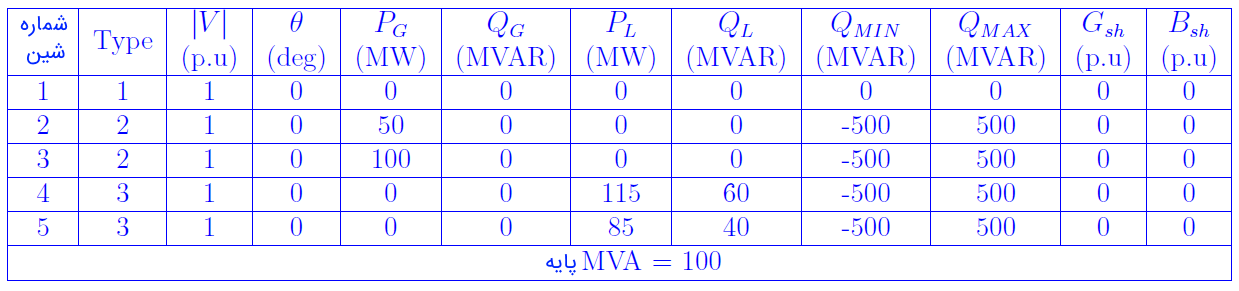
جدول ۱: اطلاعات شین‌های سیستم

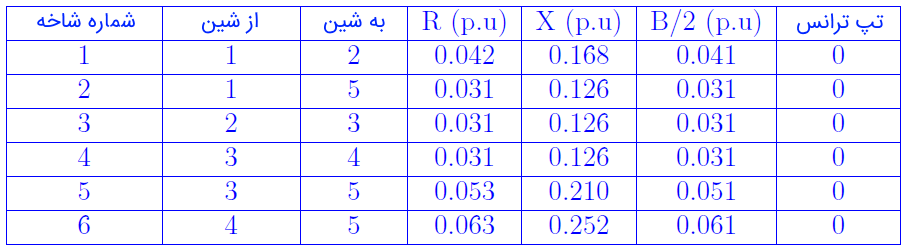
جدول ۲: اطلاعات خط‌های سیستم

از جدول ۱، توان‌های اکتیو و راکتیو شین‌های مختلف استخراج می‌شود:

$$P_2=0.5 \, \mathrm{p.u}$$

$$P_3=1.0 \, \mathrm{p.u}$$

$$P_4=-1.15 \, \mathrm{p.u}$$

$$P_5=-1.85 \, \mathrm{p.u}$$

$$Q_4=-0.6 \, \mathrm{p.u}$$

$$Q_5=-0.4 \, \mathrm{p.u}$$

همچنین، ماتریس $$\bar{\mathbf{Y}}_{\mathbf{BUS}}$$ سیستم که از اطلاعات جدول ۲ به‌دست آمده، در معادله (۴) نشان داده شده است. در این معادله، بخش حقیقی ($$\mathbf{G}$$)‌ و بخش موهومی ($$\mathbf{B}$$) ماتریس $$\bar{\mathbf{Y}}_{\mathbf{BUS}}$$ ($$\bar{\mathbf{Y}}_{\mathbf{BUS}}=\mathbf{G}+j\mathbf{B}$$) به‌صورت جداگانه نشان داده شده‌اند.

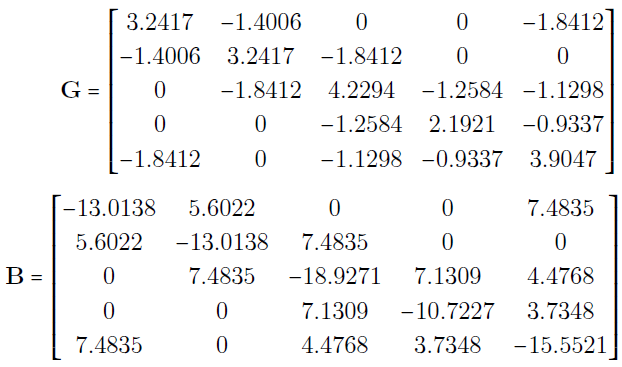
برای انجام پخش بار گوس سایدل،‌ از شروع تخت استفاده می‌کنیم. توجه کنید که پروفیل ولتاژ‌ تخت، در شین‌های PQ دنبال خواهد شد. برای شین‌های PV، مقدار اولیه ولتاژ را برابر با اندازه ولتاژ تعیین‌شده آن شین در نظر می‌گیریم. زاویه اولیه ولتاژ را نیز همیشه صفر فرض می‌کنیم. بنابراین، با توجه به اطلاعات جدول ۱، مقادیر ولتاژهای ۵ شین سیستم را $$1.0 \angle 0^ \circ$$ در نظر می‌گیریم. اکنون با توجه به اینکه سیستم، شامل شین‌های PV و PQ است، از الگوریتم پخش بار گوس سایدل کامل استفاده می‌کنیم. در گام ۲(الف) این الگوریتم، ابتدا توان راکتیو مصرفی یا تولیدی ژنراتورهای ۲ و ۳ (متناظر با $$i=2$$ و $$i=3$$) را محاسبه می‌کنیم. جدول ۳، مقادیر محاسبه‌شده $$Q_2$$ و $$Q_3$$ (برحسب پریونیت) را در تکرار ۱ نشان می‌دهد (این مقادیر با $$Q_{cal}$$ نمایش داده شده‌اند).

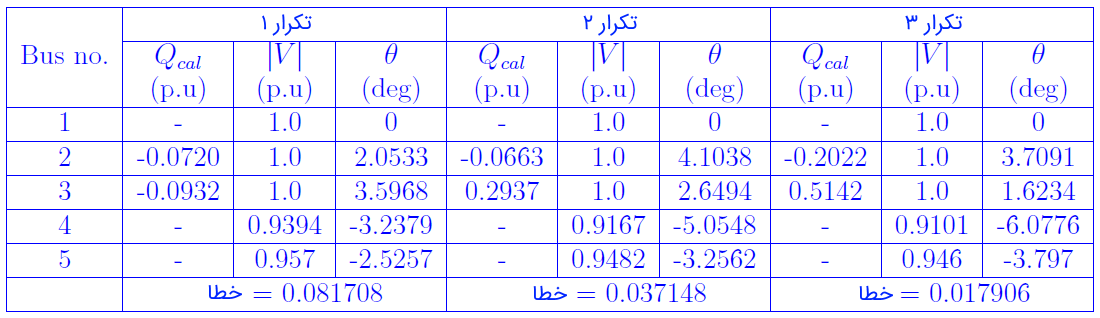
جدول ۳: نتایج پخش بار گوس سایدل بدون قید $$Q$$ برای تکرارهای ۱ تا ۳

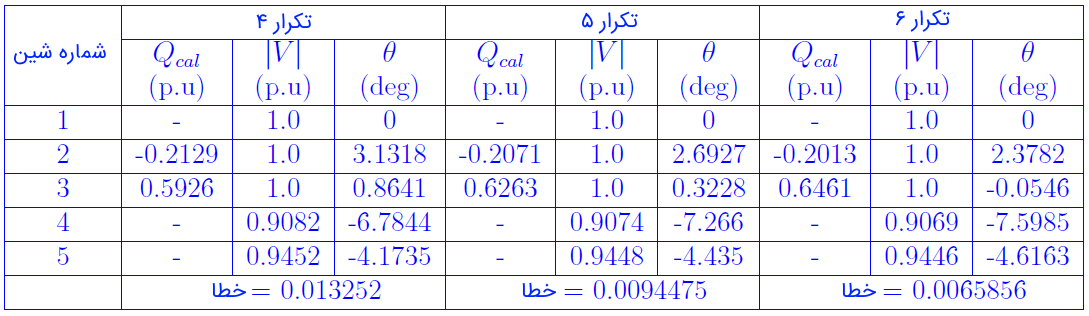
جدول ۴: نتایج پخش بار گوس سایدل بدون قید $$Q$$ برای تکرارهای ۴ تا ۶

داده‌های جدول ۱ نشان می‌دهند که حدود کمینه و بیشینه توان راکتیو دو ژنراتور به‌ترتیب، $$-5 \, \mathrm{p.u}$$ و $$5 \, \mathrm{p.u}$$ است. بنابراین، هر دو شین 2 و 3 به‌عنوان شین PV عمل می‌کنند و اندازه ولتاژ آن‌ها، مقدار تعیین‌شده اولیه است و فقط زاویه ولتاژ آن‌‌ها را باید از گام ۲(ب) محاسبه کرد (با استفاده از مقادیر محاسبه‌شده $$Q_2$$ و $$Q_3$$).

در گام ۳، اندازه و زاویه شین‌های ۴ و ۵ به‌دست می‌آیند. نتایج تکرار اول، در جدول ۳ ارائه شده است. در نهایت، در گام‌های ۴ و ۵ خطا محاسبه می‌شود. در پایان تکرار اول می‌بینیم که خطا، بیشتر از مقدار مشخص‌شده (در این‌جا $$1.0e^{-12}$$) است و در نتیجه باید الگوریتم را ادامه داد و به گام دوم بازگشت. جدول ۴ نیز نتایج حاصل از تکرارهای 4 تا ۶ را نشان می‌دهد. لازم به ذکر است که در این تکرارها، حدود $$Q_G^{max}$$ و $$Q_G^{min}$$ مربوط به دو ژنراتور رعایت شده و در شین‌های ۲ و ۳ در تکرارها به‌عنوان شین PV در نظر گرفته شده‌اند.

اگر به جدول‌های ۳ و ۴ دقت کنیم، می‌بینیم که با افزایش تکرارها خطا در حال کاهش است. با ادامه محاسبات، در نهایت، پس از 69 تکرار به نتایج جدول ۵ خواهیم رسید.

جدول ۵: نتایج نهایی پخش بار گوس سایدل

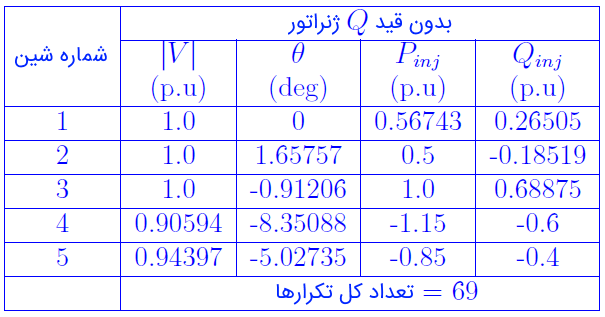
با توجه به جدول ۵، مقادیر نهایی $$Q_2$$ و $$Q_3$$ به‌ترتیب، $$-18.51$$ و $$68.87$$ مگاوار (MVAR) است. این مقادیر در محدوده مجاز توان راکتیو هستند، بنابراین، اندازه ولتاژ شین‌های ۲ و ۳ در مقدار $$1.0 \, \mathrm{p.u}$$ (مقدار مشخص‌شده از قبل) باقی می‌ماند. در نهایت، مقادیر محاسبه‌شده نهایی توان اکتیو و راکتیو تزریقی همه شین‌ها، در جدول ۵ قابل مشاهده است.

اکنون پخش بار گوس سایدل را برای حالتی بررسی می‌کنیم که قید توان راکتیو در آن رعایت نشود. بدین منظور، فرض کنید حداکثر توان راکتیوی که ژنراتور ۳ می‌تواند تأمین کند، $$50 \, \mathrm{MVAR}$$ است (وقتی قیدی وجود نداشت، ژنراتورها مقدار $$68.87 \, \mathrm{MVAR}$$ را تأمین می‌کردند). جدول‌های ۶ و ۷، شش تکرار اول محاسبات پخش بار را با فرض وجود قید حداکثر توان نشان می‌دهند. اگر جدول‌های ۳ و ۶ را مقایسه کنیم، می‌بینیم که حل پخش بار با قید Q در دو تکرار اول، شبیه حالتی است که ژنراتورها قید توان راکتیو ندارند. در تکرار ۳، مقدار $$Q_3$$‌ محاسبه‌شده، برابر با $$51.42 \, \mathrm{MVAR}$$ است. در نتیجه $$Q_3$$ به مقدار $$50 \, \mathrm{MVAR}$$ محدود می‌شود و شین ۳ به‌عنوان یک شین PQ عمل می‌کند. بنابراین، ولتاژ آن با استفاده از عبارت موجود در گام ۲(ج) به‌دست می‌آید. می‌بینیم که اندازه این ولتاژ، دیگر برابر با $$1.0 \, \mathrm{p.u}$$ نیست (در حقیقت، به‌دلیل کمبود توان راکتیو، به کم‌تر از این مقدار می‌رسد). در تکرار بعدی نیز، مقدار $$Q_3$$ همان $$50 \, \mathrm{MVAR}$$ در نظر گرفته می‌شود، در نتیجه $$|V_3|<1.0 \, \mathrm{p.u}$$ خواهد بود. در نهایت، پس از ۶۶ تکرار، الگوریتم با تلورانس $$1.0e^{-12} \mathrm{p.u}$$ همگرا می‌شود که نتایج آن در جدول ۸ قابل مشاهده است. در این جدول، نتایج پخش بار گوس سایدل بدون قید توان راکتیو نیز برای مقایسه آورده شده است.

جدول ۶: نتایج پخش بار گوس سایدل با قید $$Q$$ برای تکرارهای ۱ تا ۳

جدول ۷: نتایج پخش بار گوس سایدل با قید $$Q$$ برای تکرارهای ۴ تا ۶

جدول ۸: نتایج نهایی پخش بار گوس سایدل با قید Q ژنراتور

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• آموزش شبیه سازی سیستم های قدرت با PowerWorld Simulator
• آموزش نرم‌ افزار DIgSILENT برای آنالیز و شبیه سازی سیستم های قدرت
• پایداری سیستم قدرت — به زبان ساده
• پخش بار نیوتن رافسون در متلب — از صفر تا صد

^^