معادله اویلر لاگرانژ – به زبان ساده (+ دانلود فیلم آموزش رایگان)

مکانیک نیوتونی فضاپیمای آپولو را به سمت ماه و کاوشگر «ویجر» (Voyager) را به بیرون از منظومه شمسی فرستاد. با این حال این دیدگاه نتیجه‌‌ی یک دیدگاه کلی‌تر است. دیدگاهی که ما را به سمت مکانیک کوانتومی و نهایتا دنیای دیجیتال سوق داد. این دیدگاه است که به ما می‌گوید رفتار الکترون در حالتی که به آن نگاه می‌کنیم و در حالتی که ناظری وجود نداشته باشد، متفاوت است! از این رو در این مطلب قصد داریم تا نگاهی متفاوت به پدیده‌ها را معرفی کنیم. این دیدگاه، روش لاگرانژی یا مکانیک لاگرانژی است. از ستون‌های اصلی و ابتدایی جهت درک این دیدگاه، معادله‌ اویلر لاگرانژ است.

مطابق با شکل زیر سیستمی از جرم و فنر را در نظر بگیرید. همان‌طور که در مطلب ارتعاشات نیز بیان شد، چنین سیستمی را می‌توان با استفاده از رابطه‌ی F=ma یا $$m\ddot{x}=-kx$$ توصیف کرد. همان‌گونه که می‌دانید پاسخ چنین سیستمی به صورت سینوسی خواهد بود.

استفاده از زاویه‌ی نگاهی جدید و بدون استفاده‌ی صریح از قانون دوم نیوتون نیز می‌توان به همین پاسخ دست یافت. مکانیک لاگرانژی به نسبت قانون دوم نیوتن نگاه جامع‌تری به پدیده‌های فیزیکی دارد. با مطالعه‌ی این مطلب به مفاهیم و اصول این نگاه و هم‌چنین به حل مسائل مرتبط با مکانیک تحلیلی و لاگرانژی مسلط خواهید شد. مکانیک لاگرانژی در حساب تغییرات بسیار پرکاربرد است.

معادله اویلر لاگرانژ

به‌منظور معرفی مکانیک لاگرانژی در ابتدا فرض کنید انرژی‌های پتانسیل و جنبشی سیستمی با نماد‌های V و T نشان داده می‌شوند. در این صورت مفهومی تحت عنوان «لاگرانژین» (Lagrangian) به‌صورت زیر قابل تعریف است.

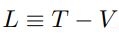
در رابطه بالا قبل از انرژی پتانسیل از علامت منفی استفاده شده است. بدیهی است که علامت مثبت نشان دهنده انرژی کل یک سیستم است. در مسئله جرم و فنر T و V به‌ترتیب برابر با $$m\dot{x}^2/2$$ و $$kx^2/2$$ هستند. در نتیجه لاگرانژین در سیستم جرم و فنر برابرند با:

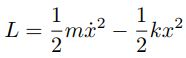
فرض کنید از رابطه فوق به‌شکل زیر مشتق جزئی گرفته شود:

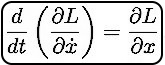
در ادامه این مطلب در مورد این‌که چرا مشتق‌گیری بالا انجام شده، بحث خواهیم کرد. به معادله دیفرانسیل بالا، «معادله اویلر-لاگرانژ» (Euler-Lagrange Equation) گفته می‌شود. برای مسئله جرم و فنر $$\partial L /\partial \dot x=m \dot x$$ و $$\partial L /\partial x=k x$$ هستند. با جایگذاری عبارات بدست آمده در رابطه ۱ معادله زیر بدست می‌آید.

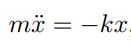
بله رابطه فوق همان معادله جرم و فنر است! به معادلاتی هم‌چون معادله بالا که از معادله اویلر-لاگرانژ بدست می‌آید، معادله حرکت گفته می‌شود. در مواردی که با دستگاه مختصاتی بیش از یک متغیر رو‌به‌رو هستیم، کافی است رابطه ۱ را به‌صورت جداگانه بر حسب هرکدام از متغیر‌ها بنویسید. بنابراین تعداد معادلات بدست آمده برابر با تعداد متغیر‌های مستقل است.

مثال ۱

مطابق با شکل زیر پاندولی به جرم m را در نظر بگیرید که به فنری که طول تعادلش L است، متصل شده.

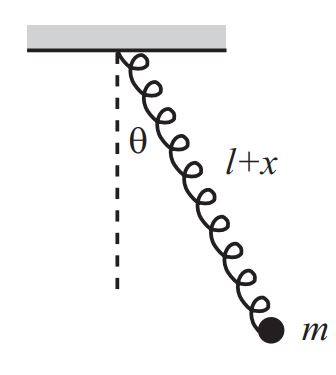
با دوران کردن جرم، طول پاندول (L+x(t شده و زاویه‌ی آن با محور عمودی برابر با (θ(t در نظر گرفته می‌شود. با فرض این‌که حرکت پاندول در صفحه‌ی دوبعدی باشد، معادله حرکت را بدست آورید.

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

پاسخ: انرژی جنبشی از دو بخشِ انرژی جنبشی مماسی و شعاعی تشکیل شده است؛ در نتیجه انرژی جنبشی سیستم برابر است با:

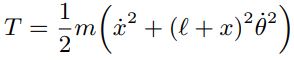
از طرفی انرژی پتانسیل، از دو بخش انرژی پتانسیل گرانشی و انرژی پتانسیلِ فنر تشکیل شده؛‌ در حقیقت انرژی پتانسیل سیستم برابر با عبارت زیر است:

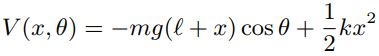
با محاسبه انرژی‌های جنبشی و پتانسیل، لاگرانژین را می‌توان به‌شکل زیر بیان کرد:

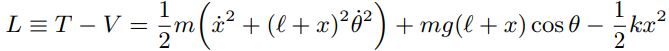
با توجه به رابطه فوق، لاگرانژی وابسته به دو متغیر θ و x است. همان‌گونه که در بالا نیز بیان شد، نکته جالب در مورد رابطه ۱ این است که می‌توان آن را به‌صورت جداگانه، برحسب هرکدام از متغیر‌ها نوشت. در این مثال، رابطه ۱ بر حسب متغیر x برابر با عبارت زیر است.

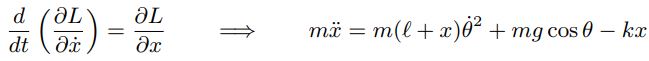
هم‌چنین رابطه‌ ۱ بر حسب θ برابر است با:

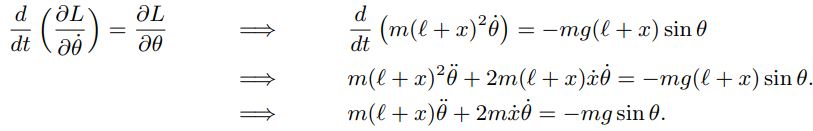
رابطه ۲ نشان دهنده قانون دوم نیوتن یا همان F=ma در حالتی است که نیروی گریز از مرکز ($$-(l+x)\dot{\theta}^2$$) نیز در نظر گرفته شده باشد. هم‌چنین خط اول در رابطه ۳ بیان کننده تغییرات تکانه زاویه‌ای در نتیجه‌ی اعمال گشتاور است.

مثال ۱ نشان می‌دهد که در هر دو حالتِ‌ استفاده از مکانیک لاگرانژی یا مکانیک نیوتنی به نتایج مشابهی دست خواهیم یافت. اما در مسائلی که چندین متغیر وابسته وجود دارد، استفاده از مکانیک لاگرانژی از نظر زمانی به صرفه‌تر خواهد بود. اما به راستی تفاوت بین این دو دیدگاه در چیست؟ در ادامه به این سوال پاسخ خواهیم داد.

اصل کم‌ترین کنش

با توجه به مطالب بیان شده در بالا، تابع لاگرانژ، وابسته به مکان و سرعت اجزاء یک سیستم است. مقدار زیر را در نظر بگیرید.

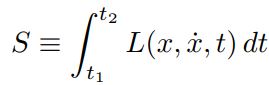
در رابطه بالا S کنش نامیده شده و بُعد آن برابر با انرژی×زمان است. بدیهی است که S وابسته به L و L نیز وابسته مختصات (x(t است. در حقیقت با تعریف هر تابعی می‌توان مقدار S را تعریف کرد. معمولا انتگرال‌های مشابه رابطه ۴ را «تابعی» (Functional) می‌نامند. هم‌چنین در برخی از متون علمی S را نماد [(S[x(t نمایش می‌دهند. نکته بسیار مهم در محاسبه S این است مقدار آن وابسته به کلِ تابع (x(t است. در ادامه خواهید دید که مفهوم S بسیار مهم است.

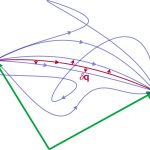
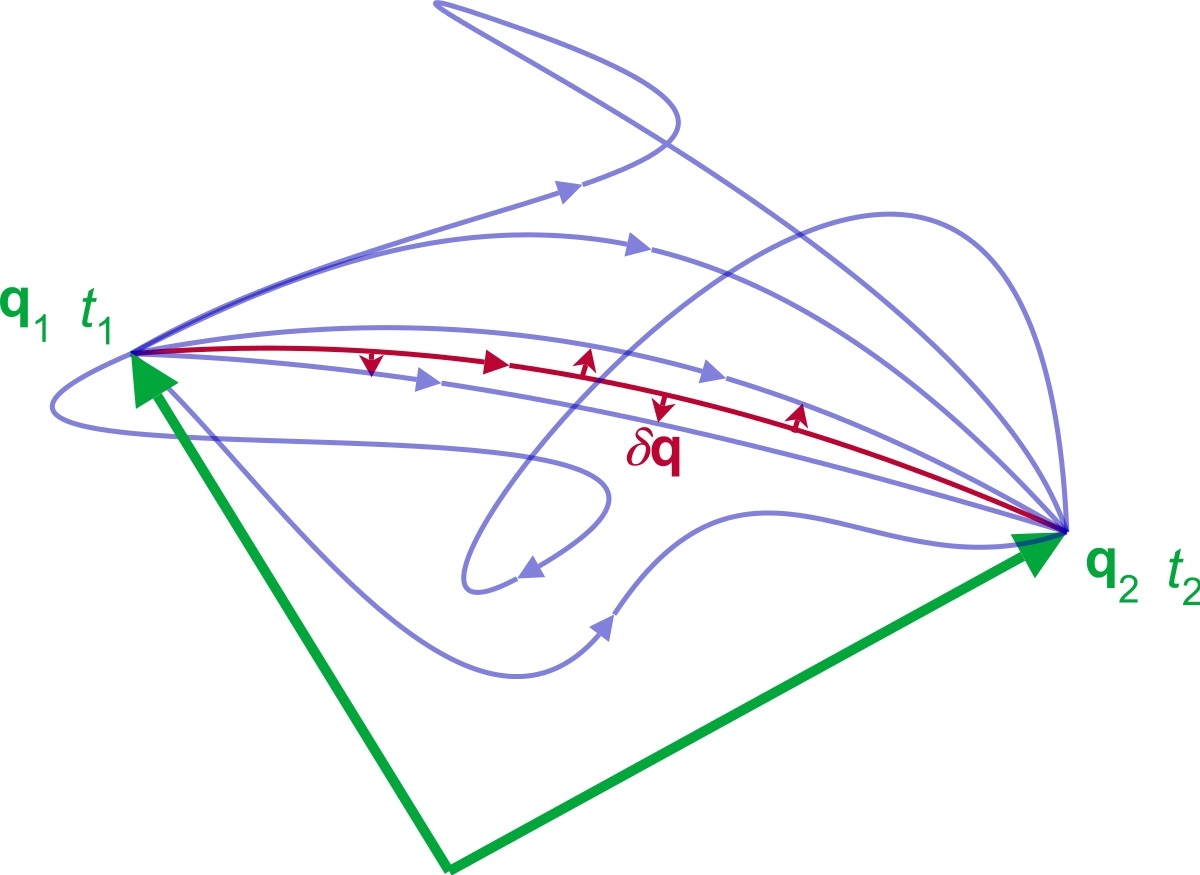
در این قسمت سوالی را مطرح می‌کنیم. تابعِ (x(t را در بازه t₁<t<t₂ در نظر بگیرید. فرض کنید نقاط ابتدا و انتهای (x(t ثابت نگه داشته شده‌اند. در حقیقت x(t₁)=x₁ و x(t₂)=x₂ نقاطی ثابت در نظر گرفته شده‌اند. توجه داشته باشید که بین نقاط ابتدا و انتها، توابع مختلفی از (x(t می‌توانند وجود داشته باشند. در شکل زیر توابع ممکن بین نقاط ابتدا و انتها نشان داده شده‌اند.

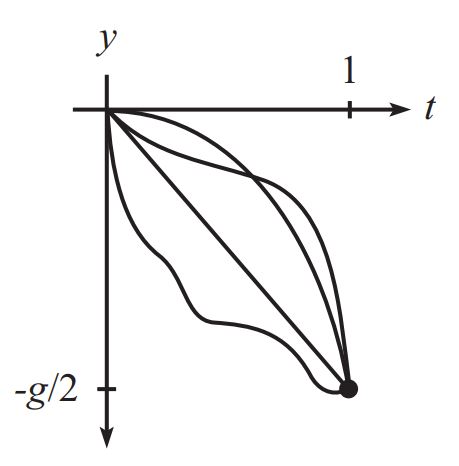
با این فرضیات به ازای چه تابعی از (x(t، کمیت S، اکسترمم می‌شود؟ برای نمونه فرض کنید توپی با سرعت اولیه‌ی صفر از ارتفاعی رها می‌شود. فرض کنید تابع (y(t موقعیت توپ را نشان می‌دهد. هم‌چنین با توجه به دستگاه مختصات در نظر گرفته شده مکان اولیه توپ برابر با y(0)=0 و مکان نهایی آن نیز $$y(1)=-g/2$$ است. همانند شکل بالا مسیر‌های زیادی را می‌توان برای توپ مذکور در نظر گرفت. هرکدام از این توابع نیز S متفاوتی را منجر می‌شوند. به نظر شما توپ کدام مسیر انتخاب می‌کند؟ به‌منظور پاسخ به این سوال از قضیه زیر استفاده می‌کنیم.

قضیه: اگر تابع (x₀(t در کمیت S قرار گرفته و آن را اکسترمم کند، تابع (x₀(t در رابطه مشتق جزئی زیر (معادله اویلر-لاگرانژ) صدق خواهد کرد. توجه داشته باشید (x₀(t تابعی است که نقاط ابتدا و انتهای آن‌ معلوم است.

اثبات قضیه‌ی بالا

جهت اثبات قضیه بالا از این واقعیت استفاده می‌کنیم که اگر تابع (x₀(t منجر به اکسترمم شدن S شود، در این صورت هر تابع دیگری نزدیک به (x₀(t (با نقاط ابتدایی وانتهایی یکسان) نیز همان S را تولید خواهد کرد. این در حقیقت تعریف نقطه سکون محسوب می‌شود. در حقیقت اگر x=b نقطه سکونِ تابع f باشد، در این صورت تابع (f(b+ε، از مشتق دوم به بالا با (f(b متفاوت خواهد بود.

دلیل درست بودن گذاره بالا صفر بودن (f^'(b در x=b است. از این رو در هنگام نوشتن بسط تیلور،‌ عبارت مربوط به مشتق اولِ f ظاهر نمی‌شود. در نتیجه فرض کنید که تابع (x₀(t منجر به مقدار سکون برای S می‌شود. هم‌چنین تابع زیر را در نظر بگیرید.

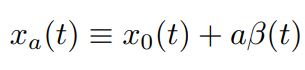
در رابطه بالا a عددی ثابت و $$\beta (t)$$ تابعی است که نقاط ابتدایی و انتهایی آن به‌ترتیب برابر با  $$\beta (t_1)=\beta (t_2)=0$$ هستند. با قرار دادن (x_a(t در رابطه ۴، کنش [(S[x_a(t تولید شده و با انتگرال‌گیری از آن، S برابر با عددی ثابت بدست می‌آید. بدیهی است که S بدست آمده به‌جای t تابعی از a خواهد بود. سوال این‌جا است که دو تابع زیرِ انتگرال، تا مشتق اول با یکدیگر برابر هستند؛ بنابراین چرا S تابعی از a شده است؟ به‌منظور پاسخ به این سوال از [(S[x_a(t، به‌صورت زنجیره‌ای مشتق می‌گیریم.

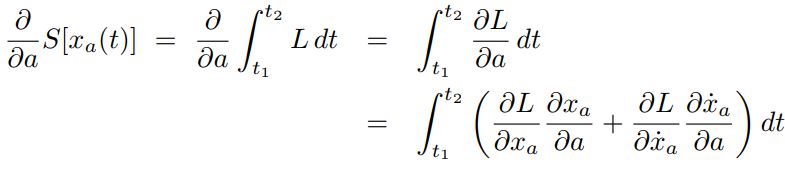
در حقیقت a در قالب x و $$\dot{x}$$، روی S تاثیر می‌گذارد. با توجه به رابطه ۵ می‌توان نوشت:

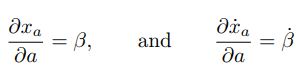
در نتیجه رابطه ۶ را می‌توان به‌شکل زیر بازنویسی کرد:

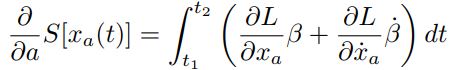
حال به بخشی از مسئله رسیده‌ایم که تفاوت هوش لاگرانژ و اویلر را با یک انسان عادی نشان می‌دهد! در این مرحله با استفاده از انتگرال‌گیری جز‌ء به جزء عبارت دوم به شکل زیر قابل بازنویسی خواهد بود.

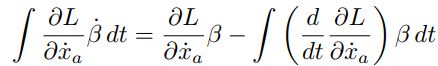
بنابراین با استفاده از رابطه فوق، رابطه ۷ به‌صورت زیر قابل نوشتن خواهد بود.

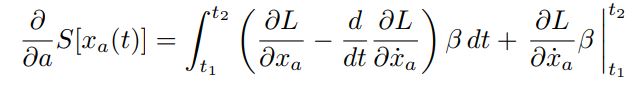
همان‌گونه که در ابتدا نیز فرض شد، مشتقات x در نقاط ابتدایی و انتهایی برابر با صفر هستند. با توجه به این که مشتقات مذکور را برابر با $$\beta$$ در نظر گرفتیم، در نتیجه $$\beta(t_1)=\beta(t_2)=0$$ هستند. حال با استفاده از این حقیقت که $$\partial S/\partial a=0$$ است، می‌توان نتیجه گرفت که عبارت درون پرانتزِ رابطه ۸ بایستی برابر صفر باشد. با صفر قرار دادن عبارت مذکور داریم:

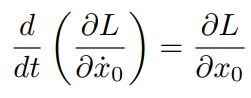
عبارت بدست آمده در بالا همان معادله اویلر لاگرانژ است. در نتیجه معادله اویلر لاگرانژ با فرض اکسترمم بودن S بدست آمده است. همان‌گونه که در بالا نیز اشاره شد با استفاده از این رابطه می‌توان معادلات حرکت یک سیستم را در زمان کوتاه‌تری بدست آورد.

حال اجازه دهید تا به مثال توپ باز گردیم. همان‌طور که دیدید سیستم که در این‌جا توپ محسوب می‌شود، مسیری را انتخاب خواهد کرد که در آن S اکسترمم باشد. از طرفی به‌منظور اکسترمم بودن S معادله اویلر لاگرانژ برای سیستم بایستی برقرار باشد. لاگرانژِ توپِ در حال سقوط برابر است با:

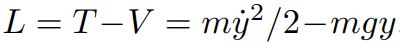
اگر L بدست آمده در بالا را در رابطه ۱ قرار دهیم، خواهیم داشت:

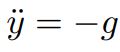
به سادگی و با دو بار انتگرال‌گیری از رابطه بالا تابع y به‌شکل زیر بدست می‌آید.

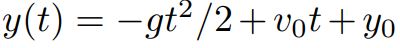
با اعمال شرایط مرزی y(0)=0 و y(1)=-g/2 شکل نهایی رابطه بالا برابر است با:

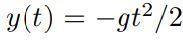
شاید مثال توپ را با استفاده از روش کلاسیک حل می‌کردیم بهتر بود. اما در زیر مثالی ارائه شده که معادلات حرکت آن را در مطلب ارتعاشات دو درجه آزادی بدست آوردیم. در این‌جا قصد داریم تا همان معادلات را با استفاده از معادله اویلر لاگرانژ بدست آوریم.

مثال ۲

در شکل زیر یک سیستم ارتعاشی دو درجه آزادی را می‌بینید. با استفاده از معادله اویلر-لاگرانژ معادلات حرکت این سیستم را بدست آورید.

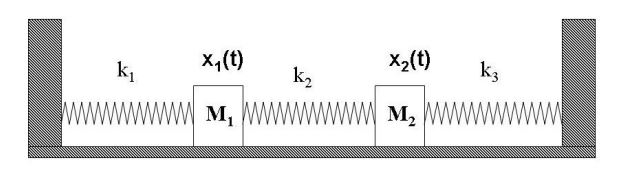
پاسخ: همان‌گونه که در تصویر فوق می‌بینید این سیستم درجه آزادیش دو بوده که با استفاده از دو مختصات (x₁(t و (x₂(t قابل توصیف هستند. انرژی جنبشی این سیستم برابر است با:

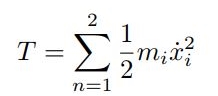
از طرفی مجموع انرژی پتانسیل ذخیره‌ شده در فنر‌ها نیز با استفاده از رابطه زیر بدست می‌آید.

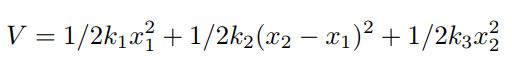
معادله اویلر لاگرانژ را نسبت به متغیر‌های x₁ و x₂، به‌طور جداگانه می‌نویسیم. با محاسبه L=T-V و قرار دادن آن در رابطه ۱، دو رابطه مذکور برابرند با:

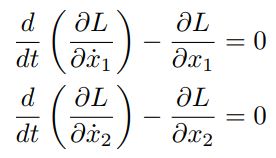
با جایگذاری T و V در رابطه فوق، به دو معادله حرکت توصیف کننده‌ی سیستم می‌رسیم.

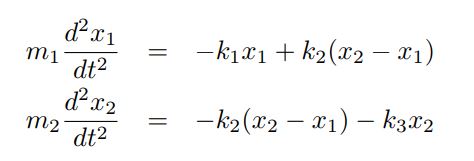
در مطلب ارتعاشات سیستم‌های دو درجه آزادی همین معادلات را با استفاده از قانون دوم نیوتن و در زمان بسیار بیشتری بدست آوردیم.

مثال ۳

مطابق با شکل زیر تابع (y(x را در نظر بگیرید. این تابع نامعلوم است، اما مقادیر آن در دو مختصات a₁ و a₂ ثابت فرض شده است. در حقیقت y(a₁)=c₁ و y(a₂)=c₂، معلوم هستند.

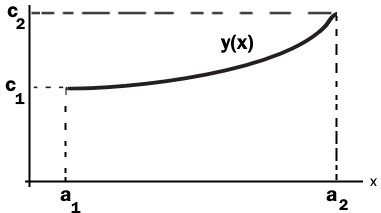
با دوران منحنی فوق حول محور x، سطحی مطابق با شکل زیر بدست می‌آید.

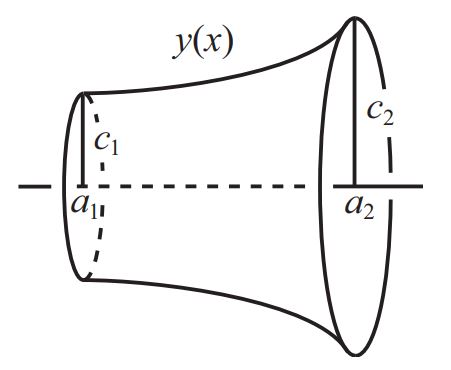
به ازای چه تابعی از y، اندازه سطح بدست آمده مینیمم است؟ این سوال را می‌توان با استفاده از دو روش حل کرد که هر دوی آن‌ها ارائه شده‌اند.

راه‌حل اول: مطابق با شکل فوق اندازه دیفرانسیل مساحت سطح برابر با $$2\pi y \enspace \sqrt {1+y'^2}dx$$ است. با انتگرال‌گیری از این تابع در بازه a₁ تا a₂، مساحت A در قالب فرمول زیر بدست می‌آید.

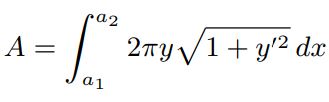
بنابراین تابع (y(x بایستی به نحوی انتخاب شود که حاصل انتگرال فوق مینیمم شود. می‌توان A را معادل با S و عبارت درون انتگرال را معادل با L تصور کرد. همچنین x در این‌جا نقش t را در قضیه کمترین کنش بازی می‌کند. در نتیجه می‌توان فرض زیر را انجام داد.

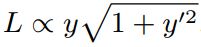
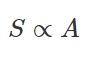
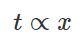
جهت مینیمم کردن S، تابع $$2\pi y \enspace \sqrt {1+y'^2}dx$$ را در معادله زیر (معادله اویلر لاگرانژ) قرار می‌دهیم.

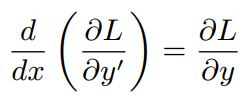
با جایگذاری و مشتق‌گیری، رابطه بالا به‌صورت زیر قابل بازنویسی می‌شود.

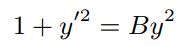
با انتخابی هوشمندانه می‌توان فهمید که تابع y، به‌صورت زیر خواهد بود.

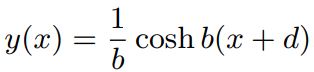
انتخاب فوق مبتنی بر رابطه زیر انجام شده است.

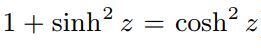
البته می‌توان با استفاده از روش جداسازی متغیر‌ها نیز به پاسخ فوق دست یافت. در این روش رابطه دیفرانسیل ۹ را می‌توان به‌شکل زیر بازنویسی کرد.

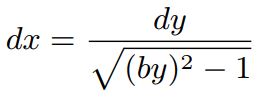
حاصل انتگرالِ $$1/ \sqrt{z^2-1}dz$$ برابر با cosh^-1z است. در نتیجه پاسخ انتگرال بالا نیز به‌صورت (cosh(x خواهد بود. در نتیجه رابطه ۱۰ به‌عنوان پاسخ، انتخاب درستی است. جهت بدست‌ آوردن ثابت‌های رابطه ۱۰، از شرایط مرزی در x=a₁ و x=a₂ استفاده می‌کنیم. با اعمال دو نقطه مذکور در رابطه ۱۰، داریم:

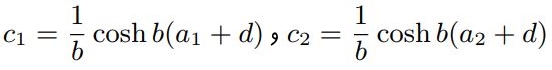
بنابراین با حل دو معادله بالا، مقادیر b و d بدست آمده و تابع y معلوم می‌شود.

راه‌حل دوم: در روش اول، با فرض کردن dx به‌عنوان دیفرانسیل، مسئله حل شد. می‌توان این مسئله را با استفاده از دیفرانسیل dy نیز محاسبه کرد. در این روش مساحت دیفرانسیلی A را برابر با تابع زیر در نظر می‌گیریم.

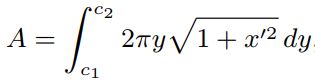
در رابطه فوق، $$x'=dx/dy$$ است. با این فرض، $$L\propto y\sqrt{1+{x'}^2}$$ بوده و معادله اویلر لاگرانژ را می‌توان به‌صورت زیر بیان کرد:

مزیت رابطه فوق نسبت به روش اول این است که سمت راست آن برابر با صفر است. در نتیجه عبارت زیر بایستی برابر با مقداری ثابت باشد.

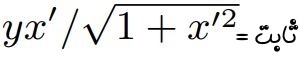
با استفاده از جداسازی متغیر‌ها، رابطه فوق به‌صورت زیر در می‌آید.

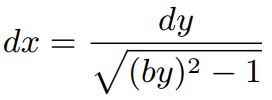
همان‌طور که می‌بینید در این روش نیز معادله دیفرانسیلی مشابه با روش اول بدست می‌آید. بنابراین می‌توان معادلات حرکت یک سیستم را به چند روش بدست آورد.

خلاصه

در این مطلب یکی از معادلات اصلی موجود در مکانیک لاگرانژی تحت عنوان معادله اویلر لاگرانژ توضیح داده شد. این معادله بیان می‌کند که انتگرالِ کمیتی تحت عنوانِ لاگرانژ که معیاری از انرژی جنبشی و پتانسیل یک سیستم محسوب می‌شود، زمانی اکسترمم است که معادله‌ی اویلر لاگرانژ برقرار باشد.

بنابراین جهت بدست آوردن معادلات حرکت یک سیستم می‌توان معادله دیفرانسیل اویلر لاگرانژ را حل کرده و از مسیر سهل‌تری به معادلات دست یافت. البته این معادله در مسائلی که می‌خواهیم کمیتی را مینیمم کنیم نیز کاربرد دارد. برای نمونه جهت مینیمم کردن طول، مساحت یا حجم، استفاده از این معادله زمان حل را بسیار کاهش می‌دهد.