نقاط ضعف الگوریتم k-means — به زبان ساده

الگوریتمهای «یادگیری نظارت نشده» (Unsupervised Learning) متعددی برای «خوشهبندی» (Clustering) دادهها مورد استفاده قرار میگیرند. الگوریتم K-Means از جمله الگوریتمهای بسیار پر کاربرد برای «تحلیل خوشه» (Cluster Analysis) به شمار میآید. برای آشنایی بیشتر با این الگوریتم، مطالعه مطلب «خوشه بندی K-Means در پایتون — راهنمای کاربردی» توصیه میشود. این الگوریتم نیز مثل سایر الگوریتمها، نقاط ضعف و قوت خاص خودش را دارد. در این مطلب به بررسی نقاط ضعف الگوریتم k-means پرداخته میشود.
بسیاری از کاربران بر این باور هستند که به منظور کار با الگوریتم k-means، به مفروضات اولیه نیازی ندارد. در واقع، با دادن یک مجموعه داده و یک عددِ تعداد خوشه از پیش تعیین شده k، میتوان این الگوریتم را روی دادهها اعمال کرد. این کار «خطای مجموع مربعات» (Sum of Squared Errors | SSE) را درون «خطای مربعات خوشه» (Cluster Squared Error) کمینه میکند. بنابراین، میتوان گفت که K-Means اساسا یک روش بهینهسازی است. برخی از نقاط ضعف الگوریتم k-means در ادامه بیان شدهاند.
- K-Means فرض میکند که واریانس توزیع هر یک از «خصیصهها» (Attribute) کروی است.
- همه متغیرها دارای واریانس مشابهی هستند.
- «توزیع احتمال پیشین» (Prior Probability) برای همه K خوشه مشابه است. بنابراین، کلیه خوشهها شامل تعداد نسبتا برابری از مشاهدات هستند.
اگر هر یک از سه فرض بیان شده در بالا برقرار نباشند، الگوریتم K-Means با خطا مواجه میشود. بنابراین، با وجود آنکه به نظر میرسد الگوریتم خوشهبندی K-Means هیچ پیشفرضی ندارد و فقط مجموع مربعات خطا (SSE) را کمینه میکند، اما در حقیقت نمیتوان ارتباط بین کمینه کردن SSE و سه فرض بیان شده را پیدا کرد.
نقاط ضعف الگوریتم k-means
مسأله بیان شده، پرسش جالب توجهی است که برای برخی از افراد مطرح میشود. طرح این پرسش، فرصت خوبی را فراهم میآورد تا مفروضات و نقاط ضعف الگوریتم k-means بررسی شوند. در همین راستا، باید دادههایی را تولید و الگوریتم را روی آنها اعمال کرد. در اینجا دو مورد از فرضیات بیان شده در بالا، در نظر گرفته میشوند. سپس، آنچه هنگام نقض مفروضات الگوریتم به وقوع میپیوندد، مورد بررسی قرار میگیرد.
در اینجا از دادههای دوبُعدی استفاده میشود، زیرا بصریسازی آنها آسانتر است (باید توجه داشت که بر اساس «مشقت چندبُعدی» (Curse of Dimensionality | طلسم ابعاد)، افزایش ابعاد موجب دشواری هر چه بیشتر مساله میشود). در اینجا از زبان برنامهنویسی آماری R استفاده میشود.
بررسی موردی با دادهسازی: اَنسکوم کوارتِت
ابتدا، مقایسهای بین مسأله بیان شده و گفتاری دیگر انجام میشود. فرض میشود که شخصی موضوع زیر را مطرح میکند.
من مطالعاتی پیرامون نقاط ضعف رگرسیون خطی داشتهام. بر همین اساس، این الگوریتم نیاز به «برآورد روندی» (Linear Trend) دارد که باقیمانده آن به طور نرمال توزیع شده است و هیچ «دورافتادگی» (Outliers) وجود ندارد. اما کاری که رگرسیون خطی انجام میدهد کمینه کردن توزیع مجموع مربعات خطا (SSE) از خط پیشبینی شده است. این یک مساله بهینهسازی است که میتوان آن را صرفنظر از شکل منحنی یا توزیع باقیماندهها حل کرد. بنابراین، رگرسیون خطی نیاز به هیچ مفروضاتی برای کار کردن ندارد.
بله؛ درست است که رگرسیون خطی با کمینه کردن مجموع مربعات باقیماندهها کار میکند. اما، این کار به خودی خود هدف رگرسیون نیست. آنچه تلاش میشود تا بتوان آن را انجام داد، ترسیم خطی است که به عنوان یک پیشبین قابل اعتماد و بدون سوگیری از y بر مبنای x عمل میکند. نظریه گوس-مارکف میگوید که کمینه کردن SSE موجب به دست آوردن هدف میشود، اما این نظریه بر برخی از مفروضات خاص تکیه دارد.
اگر این مفروضات نقض شوند، همچنان میتوان SSE را کمینه کرد، اما ممکن است الگوریتم کاری که باید انجام دهد را به خوبی پیش نبرد و یا حتی با خطا مواجه شود. شما یک خودرو را با فشردن پدال میرانید، در نتیجه، به بیان شفافتر باید گفت: «رانندگی فرایند فشردن پدال است. پدال را میتوان صرف نظر از اینکه چه مقدار بنزین در باک وجود دارد فشار داد. بنابراین، حتی اگر باک خالی باشد، همچنان میتوان پدال را فشار داد و خودرو را راند». اما حرف زدن راحت است. اکنون باید در مقام عمل، نگاهی به دادههای ساخته شده (دادهسازی انجام شده است) انداخت.

دادههای ساخته شده «اَنسکوم کوارتِت» (Anscombe's Quartet)، از جمله دادههای محبوب به شمار میآیند که در سال ۱۹۷۳ توسط «فرانک اَنسکوم» (Francis Anscombe)، آماردان انگلیسی، ساخته شدهاند. این مجموعه داده فوقالعاده، ضعفهای موجود در روشهای آماری مورد اعتماد را نشان میدهد. هر یک از مجموعه دادهها دارای شیب رگرسیون خطی، عرض از مبدا، p-value و R2 مشابهی هستند. با این وجود، با یک نگاه به تصویر بالا میتوان مشاهده کرد که تنها یکی از آنها یعنی l، مجموعه داده مناسبی برای رگرسیون خطی است. II شکل اشتباهی دارد، III دارای چولگی ایجاد شده به دلیل یک دورافتادگی است و در IV اصلا هیچ روندی وجود ندارد.
ممکن است این موضوع مطرح شود که رگرسیون خطی در شرایط موجود در موارد III ،II و IV نیز کار میکند، زیرا مجموع مربعات باقیماندهها را کمینه میکند. اما این یک پیروزی ظاهری است. رگرسیون خطی همیشه یک خط ترسیم میکند، اما اگر این خط هیچ معنایی نداشته باشد چه؟ اکنون میتوان مشاهده کرد که صرفا قابل انجام بودن بهینهسازی به معنای آن نیست که در نهایت میتوان به هدف مساله رسید. همچنین، میتوان مشاهده کرد که ساخت دادهها و بصریسازی آنها، راهکار خوبی برای بررسی مفروضات مدل است. در ادامه، از این رویکرد برای بررسی بیشتر نقاط ضعف الگوریتم k-means استفاده خواهد شد.
فرضیات دارای مشکل: دادههای غیر کُروی
این پرسش مطرح است که آیا الگوریتم k-means به خوبی روی خوشههای غیر کروی نیز کار میکند یا خیر؟ در واقع آیا میتوان خوشههای غیر کروی مانند آنچه در تصویر زیر آمده داشت؟
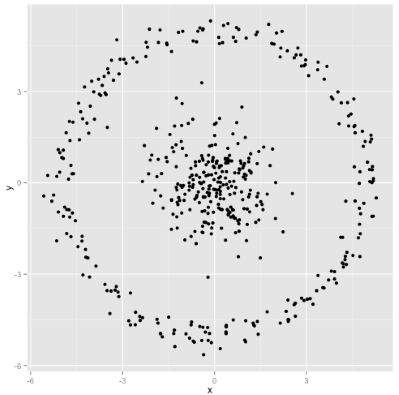
ممکن است آنچه در تصویر آمده، مطابق انتظار کاربر نباشد. اما راهکار بسیار خوبی برای ساخت خوشهها و ارزیابی روش محسوب میشود. با نگاه به تصویر، انسان میتواند سریعا تشخیص بدهد که دو گروه طبیعی از نقاط داده وجود دارند. اما اکنون باید دید که الگوریتم k-means چه تصوری از این نقاط داده دارد.
خوشهبندی k-means انجام شده روی دادهها در تصویر زیر مشخص است. خوشهها به دو رنگ مختلف آبی و نارنجی هستند و مراکز خوشهها با علامت ضربدر مشخص شده است.
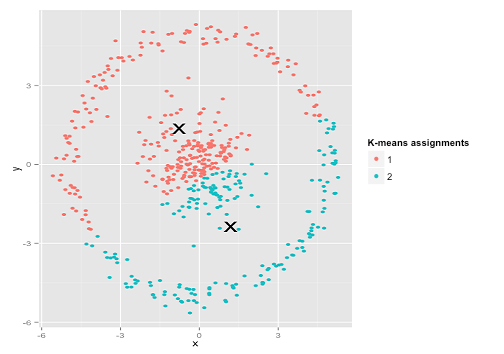
از تصویر مشخص است که k-means تلاش خودش برای ساخت خوشه را انجام داده و برای کرههای موجود در نقاط داده، مرکزهای جالبی را در نظر گرفته است. با وجود آنکه k-means هنوز هم مجموع مربعات درون خوشهای را کمینه کرده، اما صرفا به یک پیروزی ظاهری دست یافته و خروجی آن در عمل اشتباه است. اکنون، از «خوشهبندی سلسلهمراتبی» (Hierarchical clustering) روی همین دادهها استفاده میشود. خروجی این خوشهبندی در تصویر زیر قابل مشاهده است.
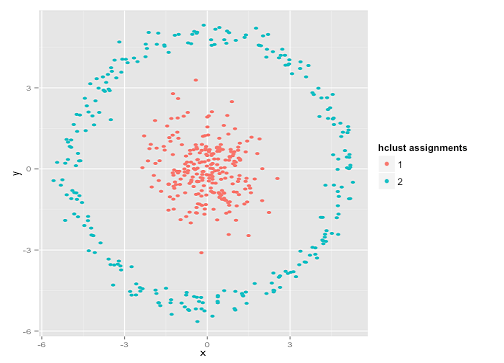
خوشهبندی سلسله مراتبی به هدف مساله رسید. دلیل این امر آن است که «خوشهبندی سلسلهمراتبی تکپیوندی» (Single-Linkage Hierarchical Clustering) فرضیات صحیحی برای این مجموعه داده دارد. البته، این روش نیز در بسیاری از مسائل دیگر با شکست مواجه میشود و عملکرد خوب آن در این دسته از مسائل الزاما به معنای عاری از اشکال بودن روش نیست. برخی از افراد ممکن است چنین تصور کنند که مسائلی با چنین نقاط دادهای بسیار نادر هستند.
اما در حقیقت چنین نیست و حالتهای دیگری مانند شرایطی که نقاط داده به جای دایره، یک نیمدایره را تشکیل دهند نیز وجود دارند که عملکرد k-means در آنها بسیار بد است. مسائل دوبُعدی را معمولا میتوان به سادگی حل کرد و معمولا مشکلات با افزایش ابعاد دادهها است که ظاهر میشوند. در نهایت باید به این نکته اشاره کرد که k-means را میتوان از دام این خطا بیرون آورد. برای این کار، باید دادهها را به مختصات قطبی تبدیل کرد. اکنون، مجددا خوشهبندی k-means روی دادهها انجام میشود که خروجی آن در تصویر زیر قابل مشاهده است.
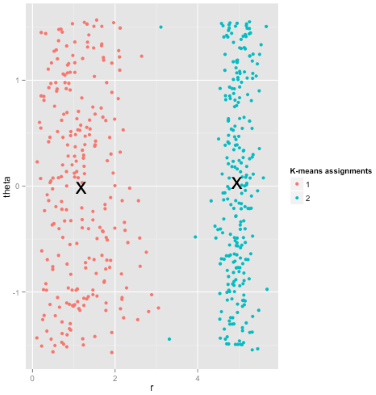
به همین دلیل است که آگاهی از مفروضات یک متد برای به کارگیری آن امری حیاتی محسوب میشود. این مفروضات نه تنها مشخص میکند که یک روش چه نقاط ضعفی دارد، بلکه نشان می دهد که چگونه میتوان این مشکلات را حل کرد.
فرضیات دارای مشکل: خوشههایی با اندازههای نامتوازن
پرسشی که در این وهله مطرح میشود این است که اگر خوشهها دارای نقاط دادهای نامتوازن باشند چه اتفاقی میافتد؟ آیا در این حالت نیز الگوریتم با شکست مواجه میشود؟ برای پاسخ دادن به این پرسش، چنین فرض میشود که مجموعهای از خوشهها با اندازه ۲۰، ۱۰۰ و ۵۰۰ وجود دارد.
هر یک از خوشهها از توزیع «گوسی چند متغیره» (Multivariate Gaussian) تولید شدهاند.
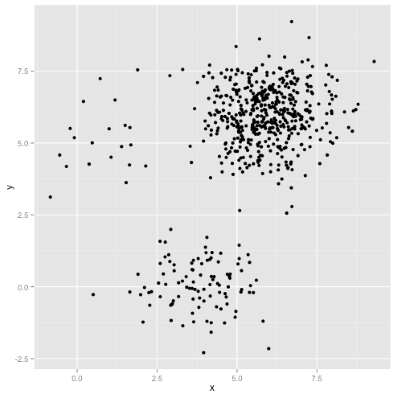
چنین به نظر میرسد که خوشهبندی k-means قادر به پیدا کردن خوشهها باشد؛ زیرا نقاط داده در گروههای کروی و منسجمی قرار داند. اکنون الگوریتم k-means روی مساله اعمال میشود. خروجی، به صورت زیر است.
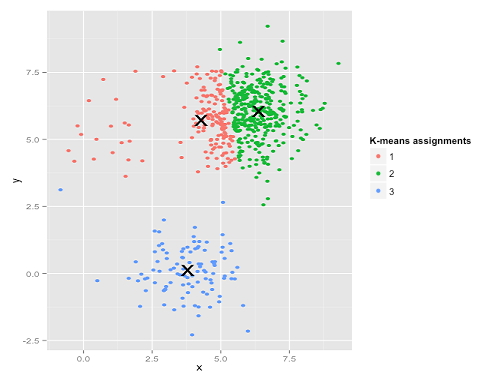
به نظر میرسد یکی دیگر از نقاط ضعف الگوریتم k-means در حال خودنمایی است. k-means در تلاش برای به حداقل رساندن مجموع مربعات درون خوشهای است و وزن بیشتری به خوشههای بزرگتر میدهد. در عمل، این بدین معنا است که k-means از اینکه خوشهها در فاصله دورتری از سایر خوشهها قرار دارند رضایت دارد، در حالی که از این مرکزها برای تقسیم خوشههای بزرگتر استفاده میکند. در صورتی که با این دادهها بیشتر کار شود، میتوان حالات بیشتر دیگری را نیز یافت که k-means در آنها عملکرد خوبی ندارد.
جمعبندی
یک نظریه جالب با عنوان «بدون ناهار مجانی» در فولکلور ریاضی وجود دارد که توسط «وُلپُرت» (Wolpert) و «مَکرِدی» (Macready) ارائه شده است. این نظریه، در فلسفه یادگیری ماشین نیز کاربرد دارد. ایده اصلی نظریه بدون ناهار مجانی از این قرار است: «هنگامی که همه شرایط در حالت متوسط خود قرار دارند، همه الگوریتمها تقریبا به یک اندازه خوب عمل میکنند». شاید آنچه گفته شد عجیب به نظر برسد. در ادامه، مفهوم مورد نظر به شکل شفافتری بیان میشود. میتوان شرایطی ایجاد کرد که یک الگوریتم رگرسیون خطی با شکست بدی مواجه شود.
رگرسیون خطی فرض میکند که دادهها در طول یک خط قرار دارند. حال میتوان عملکرد این الگوریتم را در حالتی متصور شد که نقاط به صورت یک موج سینوسی هستند. همچنین، t-test فرض میکند که هر نمونه از توزیع نرمال میآید. حال اگر یک دورافتادگی در دادهها وجود داشته باشد عملکرد این روش زیر سوال میرود. الگوریتم «گرادیان افزایشی» (Gradient Ascent) در بیشینه محلی به تله میافتد و در کل، هر روش «یادگیری نظارت شدهای» (Supervised Learning) ممکن است دچار «بیشبرازش» (Overfitting) شود.
اما همه اینها به چه معناست؟ این یعنی قدرت کاربر از فرضیات الگوریتمها نشات گرفته شده است. برای مثال، هنگامی که «نتفلیکس» (Netflix) فیلمهایی را به کاربر «پیشنهاد» (Recommend) میدهد، چنین فرض میکند که اگر کاربر یک فیلم را دوست داشته است، دیگر فیلمهای مشابه آن را نیز دوست خواهد داشت. همانطور که نمیتوان یک «سیستم پیشنهادگر» (Recommender System) را بدون در نظر گرفتن فرضیاتی پیرامون سلیقه و ذائقه کاربر ساخت، نمیتوان یک الگوریتم خوشهبندی را نیز بدون در نظر داشتن ماهیت این ساختارها ایجاد کرد. بنابراین، صرفا پذیرش ضعفهای یک الگوریتم کافی نیست. بلکه، باید نقاط ضعف الگوریتمها را شناخت و از این آگاهی برای انتخاب الگوریتم مناسب استفاده کرد. بنابراین، میتوان الگوریتم را تنظیم کرد و دادهها را برای حل مساله به آن سپرد.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دادهکاوی و یادگیری ماشین
- آموزش دادهکاوی (Data Mining) در متلب
- مجموعه آموزشهای آمار و احتمالات
- دادهکاوی (Data Mining) — از صفر تا صد
- یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
- روشهای ارزیابی نتایج خوشهبندی (Clustering Performance) — معیارهای درونی (Internal Index)
- روشهای ارزیابی نتایج خوشهبندی (Clustering Performance) — معیارهای بیرونی (External Index)
^^













سلام برای فهم بهتر یک مقاله کد شده را در سایت بارگذاری کنید
با سلام؛
از همراهی شما با مجله فرادرس سپاسگزاریم. برای مطالعه بیشتر پیرامون الگوریتم K-Means، همراه با مثال و پیادهسازی، مطلب زیر پیشنهاد میشود.
خوشه بندی k میانگین (k-means Clustering) — به همراه کدهای R
پیروز، شاد و تندرست باشید.
چقدر خوب میشد اگه منبع ها یا مقالات مرتبط با این پست را هم ذکر می کردید.خیلی ممنون از مطلب خوبتون
سلام، وقت شما بخیر؛
در انتهای هر مطلب بدون استثنا منابع آن مطلب ذکر و هاپیرلینک شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما سپاسگزاریم.