روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index)

از آنجایی که برخلاف عملیات «تحلیل ردهبندی» (Classification)، «خوشهبندی» (Clustering) یک فرآیند «بدون نظارت» (Unsupervised) است، بررسی صحت نتیجه خوشهبندی به راحتی امکانپذیر نیست. بنابراین احتیاج به معیارهای مناسب، هم برای بررسی کارایی یک روش خوشهبندی در بازیابی خوشهها و هم برای مقایسه عملکرد روشهای مختلف خوشهبندی، ضروری به نظر میرسد. در این میان دو گونه معیار ارزیابی نتایج خوشهبندی وجود دارد. معیارهای ارزیابی درونی (Internal Criteria Index) و معیارهای ارزیابی بیرونی (External Criteria index).
برای آشنایی بیشتر با شیوه خوشهبندی مطلب آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن و به منظور آگاهی از معیارهای بیرونی مطلب روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index) را مطالعه کنید. در ادامه به بررسی معیارهای ارزیابی درونی میپردازیم.
ارزیابی نتایج خوشهبندی: معیارهای درونی
هدف از بررسی معیارهای درونی، ارزیابی ساختار خوشههای ایجاده شده توسط الگوریتمهای خوشهبندی است. برای سنجش صحت نتایج خوشهبندی، ملاکها و معیارهای متفاوتی معرفی شده است. این شاخصها سعی در اندازهگیری میزان شباهت اعضای درون خوشه و عدم شباهت بین خوشهها دارند. بنابراین روشی که بیشترین شباهت درون خوشه یا بیشترین تمایز بین خوشهها را ایجاد کند، روش مناسبی در نظر گرفته میشود.
برای مثال بر اساس دادههای تک بعدی، امکان تفکیک میزان پراکندگی کل دادهها نسبت به میانگینشان به دو جزء درون خوشه و بین خوشه به کمک «تحلیل واریانس» (Analysis of Variance)، وجود دارد. بنابراین هدف، به دست آوردن خوشهبندی است که میزان پراکندگی درون خوشهای کمتری داشته باشد، یا به طور مشابه میزان پراکندگی بین خوشهای بیشتری داشته باشد.
در حالتیکه بعد دادهها، بیشتر از 1 باشد، امکان استفاده از چنین تحلیلی به راحتی وجود ندارد. بنابراین سیاستهای دیگری اتخاذ میشود. برای مثال اگر دادههای X که p بعدی هستند را با استفاده از روش خوشهبندی k-میانگین به k خوشه تفکیک کرده باشیم، میتوان میزان پراکندگی کل را با T نشان داد و به صورت زیر محاسبه کرد:
در این رابطه، تعداد دادهها در خوشهی iام و نیز مشاهدهی jام از خوشهی iام است. همچنین k نیز تعداد خوشهها است. به این ترتیب اگر W میزان پراکندگی درون و B میزان پراکندگی بین خوشهها باشد، روابط زیر برقرارند:
میتوان به راحتی نشان داد که بین این سه جزء رابطه T=B+W همیشه وجود دارد.
در این میان، خوشهبندی که پراکندگی درون خوشههایش (W) کمینه یا پراکندگی بین خوشههایش (B) بیشینه باشد، مناسبترین روش خوشهبندی است. در ادامه به معرفی چند شاخص ارزیابی درونی میپردازیم که در «خوشهبندی تفکیکی» (Partition Clustering) کاربرد بیشتری دارند.
ریشه میانگین مربعات انحراف استاندارد (RMSSTD)
برای مشخص کردن تعداد خوشهها در خوشهبندی تفکیکی میتوان از شاخص ریشه میانگین مربعات انحراف استاندارد (Root-mean-square standard deviation) استفاده کرد. این شاخص میزان شباهت مقدارهای درون خوشهها را اندازهگیری میکند. برای محاسبه شاخص RMSSTD ابتدا باید با بعضی از مفاهیم آشنا شویم.
مجموع مربعات (Sum of Square)
فرض کنید مجموعه D شامل n نقطه p بعدی باشد. یعنی .
آنگاه منظور از مجموع مربعات مقدارهای X، محاسبه رابطه زیر است:
به این ترتیب علامتهای زیر را تعریف میکنیم.
- : مجموع مربعات درون گروه = W
- : مجموع مربعات بین گروهها = B
- : مجموع مربعات مقادیر = T
حال اگر k تعداد خوشهها و p نیز بُعد دادهها باشد، آنگاه شاخص RMSSTD به صورت زیر محاسبه میشود:
همانطور که از اسم این شاخص نیز پیدا بود، مقدار ریشه (توان 1/2) میانگین مربعات درون گروهها را نشان میدهد.
برای تعیین بهترین تعداد خوشه، برای مثال در روش خوشهبندی k-میانگین، کافی است RMSSTD را به ازای مقدارهای مختلف k محاسبه و در یک نمودار به صورت زیر ترسیم کنیم. در نقطهای از محور افقی که شیب منحنی دارای تغییر محسوسی باشد، مناسبترین خوشهبندی صورت گرفته است زیرا بعد از این شکستگی، با افزایش تعداد خوشهها، تغییر زیادی در شاخص RMSSTD رخ نمیدهد. این نمودار را با نام «آرنج» (Elbow) میشناسند زیرا خمیدگی آن شبیه آرنج دست است.
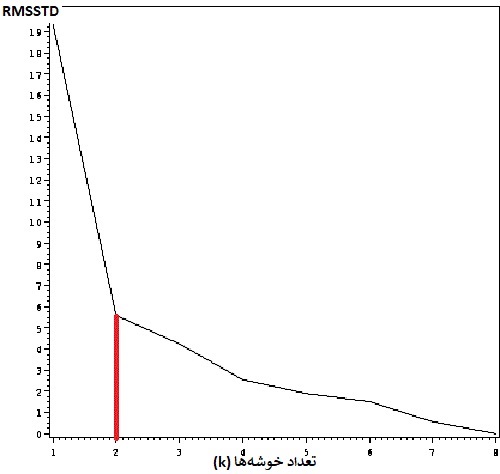
این نمودار نشان میدهد که اگر تعداد خوشهها (k) را برابر با ۲ انتخاب کنیم، به تعداد خوشههای بهینه رسیدهایم. البته با افزایش تعداد خوشهها، شاخص RMSSTD باز هم کمتر خواهد شد ولی تغییر آن خیلی محسوس نیست و ممکن است با افزایش تعداد خوشهها تفسیرپذیری آنها کاهش بیابد و یا دچار بیشبرازش شویم.
همانطور که دیده میشود، در این شاخص از معیار پراکندگی درون خوشهها برای ارزیابی استفاده شده است. پس هر چه مقدار شاخص RMSSTD کمتر باشد، عمل خوشهبندی بهتر صورت گرفته است.
شاخص ارزیابی دیویس-بولدین (Davies-Bouldin)
این شاخص توسط دیویس و بولدین دو دانشمند در رشته برق در سال 1979 معرفی شد و وابسته به تعداد خوشهها و یا الگوریتم خوشهبندی نیست. برای محاسبه این شاخص ابتدا باید با دو معیار «اندازه پراکندگی» (Dispersion measure) و «عدم شباهت بین خوشهها» (Cluster dissimilarity) آشنا شویم.
اندازه پراکندگی درون خوشه
فرض کنید میزان پراکندگی مربوط به خوشه و d نیز یک تابع فاصله باشد. آنگاه میزان پراکندگی برای این خوشه توسط رابطه زیر قابل محاسبه است:
این رابطه در حقیقت شبیه فاصله مینکوفسکی نقطههای هر خوشه از مراکز آن است.
عدم شباهت (فاصله) بین خوشهها
فاصله بین دو خوشه نیز بر اساس فاصله بین دو نقطه مرکزی آنها سنجیده میشود. اگر و مراکز خوشههای i و j باشند، فاصله بین این دو خوشه با نشان داده شده و توسط رابطه زیر بدست میآید:
باز هم به نظر میرسد از فاصله مینکوفسکی برای سنجش فاصله بین دو خوشه استفاده شده است.
حال با توجه به این دو مفهوم میتوان میزان فاصله بین دو خوشه و را که با نشان میدهیم به صورت زیر محاسبه کنیم:
همانطور که دیده میشود در صورت کسر، میزان پراکندگی دو خوشه با یکدیگر جمع شده و در مخرج نیز میزان عدم شباهت بین خوشهها قرار گرفته است. هر چه خوشهها دارای پراکندگی بیشتری باشند، مقدار بزرگتر میشود. از طرفی اگر دو خوشه با یکدیگر فاصله کمتری داشته باشند باز هم بزرگ میشود.
به این ترتیب برای محاسبه شاخص دیویس-بولدین برای یک روش خوشهبندی کافی است ابتدا بیشنیه فاصله هر خوشه را نسبت به خوشههای دیگر بدست آورد. یعنی برای خوشه iام خواهیم داشت:
سپس میانگین بیشینه فاصلههای محاسبه شده برای همه خوشههای ایجاد شده توسط الگوریتم را محاسبه میکنیم. این شاخص را با نشان میدهند.
در حقیقت این شاخص، میانگین حداکثر نسبت پراکندگی درون به پراکندگی بین خوشهها را محاسبه میکند. هر چه مقدار شاخص کمتر باشد، عمل خوشهبندی بهتر صورت گرفته است.
نکته: مقدار t و r از یکدیگر مستقل هستند. انتخاب تابع فاصله نیز در این شاخص براساس دادهها و رفتار آنها انجام میشود.
شاخص دان (Dunn's Index)
«خانواده شاخصهای دان» (Dunn family indices) در سال 1974 طی مقالهای با توجه به مفهوم «فشردگی» (Compactness) و «تفکیکپذیری» (Separation) توسط دان معرفی شدند. او با دو معیار «فاصله» (Cluster Distance) و قطر (Diameter)، میزان فشردگی و تفکیکپذیری را محاسبه کرد.
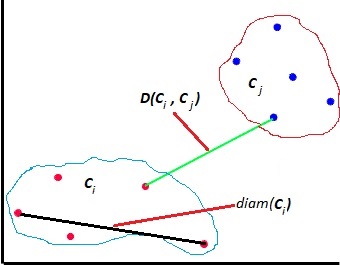
حال اگر فاصله بین دو خوشه و را با نشان دهیم، میتوانیم میزان تفکیکپذیری در خوشهبندی را به صورت زیر محاسبه کنیم:
همینطور برای اندازهگیری فشردگی خوشهها، از قطر هر خوشه استفاده میشود. برای خوشه مقدار قطر توسط رابطه زیر بدست میآید.
حال شاخص دان به صورت زیر تعریف میشود.
در صورت این کسر، فاصله بین دو خوشه به عنوان معیاری برای تفکیکپذیری دیده میشود و در مخرج نیز قطر هر خوشه دیده میشود. نسبت این دو، مقیاسی برای سنجش فاصله بین دو خوشه خواهد بود. بنابراین کوچکترین مقدار این نسبت برای همه خوشهها، میتواند شاخصی برای ارزیابی خوشهبندی باشد. هر چه مقدار این شاخص بزرگتر باشد، بیانگر تفکیکپذیری بهتر و در نتیجه خوشهبندی موثرتر است. بر همین اساس اگر نسبت میزان تفکیکپذیری به قطر خوشهها مقدار بزرگی باشد، خوشهبندی به خوبی انجام شده است.
معیار نیمرخ (Silhouette)
یکی دیگر از روشهای ارزیابی خوشهبندی، معیار «نیمرخ» (Silhouette) است. این معیار هم به پیوستگی (Cohesion) درون خوشهها و هم به میزان تفکیکپذیری آنها بستگی دارد. مقدار نیمرخ برای هر نقطه، میزان تعلق آن را به خوشهاش در مقایسه با خوشه مجاور اندازه میگیرد.
فرض کنید نقطهای مانند در میان دادههایی که خوشهبندی کردهاید وجود دارد و در طی مراحل خوشهبندی نیز k خوشه () ایجاد شده است. برای محاسبه معیار نیمرخ احتیاج به آشنایی با دو مفهوم اصلی داریم:
میانگین فاصله یک نقطه از خوشه با نقاط دیگر آن خوشه: این مقدار را با نشان داده و به صورت زیر محاسبه میکنیم.
این معیار را میتوان ملاکی برای ارزیابی تعلق نقطه در خوشهاش در نظر گرفت. هر چه مقدار کوچکتر باشد، میزان تعلق این نقطه به خوشهاش بیشتر است.
نکته: این معیار میتواند براساس بیشتر توابع فاصله، مانند فاصله اقلیدسی و منهتن نیز محاسبه شود.
حداقل میانگین فاصله نقطه با خوشههای دیگر: فرض کنید نقطه به خوشه تعلق دارد. حال میانگین فاصله این نقطه را با نقاط خوشههای دیگر (مثلا ) اندازه میگیریم. خوشهای که دارای کمترین میانگین فاصله برای نقطه باشد، به عنوان خوشه مجاور با این نقطه نامیده میشود. مقدار میانگین فاصله نقطه با نقاط خوشه مجاور را با نشان میدهیم.
به این ترتیب میزان معیار نیمرخ برای نقطه بوسیله رابطه زیر اندازهگیری میشود:
در نتیجه اگر کوچکتر از باشد، مقدار شاخص نیمرخ مثبت میشود و برعکس اگر کوچکتر از باشد، مقدار شاخص نیمرخ منفی شده و نشانگر خوشهبندی ضعیف است زیرا نقطه بیش از آنکه شبیه خوشه خودش باشد به خوشه مجاور شباهت دارد. با توجه به رابطه بالا مقدار این شاخص بین ۱- تا ۱+ تغییر میکند. مقدار نزدیک به ۱ بیانگر انطباق خوب بین نقطه و خوشهاش نسبت به خوشه مجاور است. اگر معیار نیمرخ برای همه نقاط درون خوشهها نزدیک به ۱ باشد، عمل خوشهبندی به درستی انجام شده است. در حالیکه کوچک بودن مقدار نیمرخ برای خوشهها، بیانگر ضعیف بودن نتایج خوشهبندی است که ممکن است به علت انتخاب نامناسب تعداد خوشهها (k) نیز باشد.
حال اگر میانگین مقدار نیمرخ برای نقطهای هر خوشه را محاسبه کنیم، معیاری برای ارزیابی هر خوشه بدست میآید. همچنین میانگین کل مقدارهای نیمرخ نیز معیاری برای ارزیابی عملیات خوشهبندی محسوب میشود.
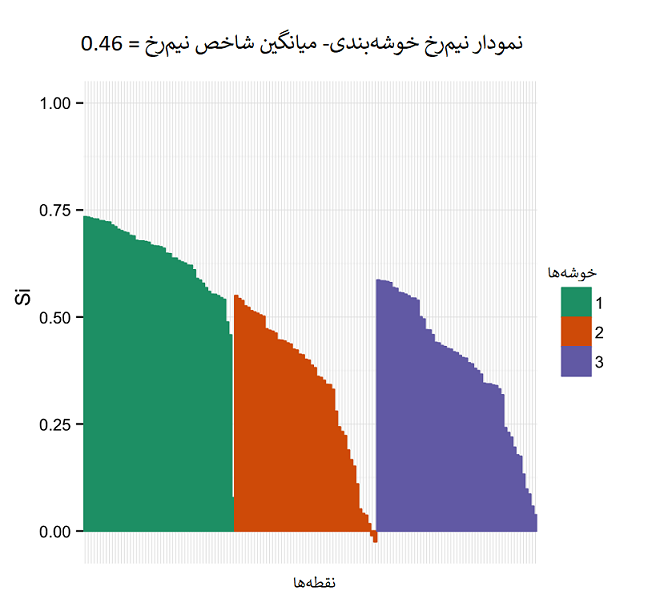
برای تفسیر این معیار، از نموداری استفاده میشود که میزان انطباق هر نقطه را با خوشه خودش نمایش میدهد. در تصویر زیر این نمودار دیده میشود. محور افقی نقطهها و ستونها، مقدار معیار نیمرخ برای آن نقطه است. همچنین میانگین شاخص نیمرخ برای همه نقاط نیز در نمودار مشخص میشود. همانطور که در نمودار دیده میشود، برای خوشه شماره ۲ بعضی نقاط دارای مقدار نیمرخ منفی هستند که نشان میدهد ممکن است به درستی خوشهبندی نشده باشند و به خوشه مجاور تعلق داشته باشند. همچنین میانگین کل شاخص نیمرخ نیز برابر با 0.46 محاسبه شده است.
اگر به یادگیری مباحث مشابه این مطلب علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
- روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index)
- آموزش خوشه بندی تفکیکی با نرم افزار R
- آموزش خوشه بندی سلسله مراتبی با SPSS
- آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن
- فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی
^^













با سلام
ممنون از مطلب خوبتون. میشه رفرنس این مطلب رو داشته باشم؟
سلام، وقت شما بخیر؛
منبع تمامی مطالب مجله فرادرس در انتهای آنها ذکر شدهاند.
از همراهی شما و ارائه بازخوردتان بسیار سپاسگزاریم.
عرض سلام و احترام
ضمن تشکر از مطالب خیلی خوبتون، یک سوال داشتم از خدمتتون، آیا امکان محاسبه شاخص دیویس-بولدین در نرم افزار SPSS هست؟اگر بله میشه بفرمائید در کدام دستور نرم افزار این شاخص محاسبه می شود.
خیلی ممنون.
سلام وقت بخیر
با تشکر از توضیحات خوبتون
یه سوال در مورد ارزیابی خوشه بندی با استفاده از روشهای مثل دیویس-بولدین داشتم
امکانش هست بعد از خوشه بندی داده که از روش مجموع مربعات فاصله درون خوشه ای به عنوان تابع هدف استفاده شده نتیجه خوشه بندی رو با این روشها مثل دیویس-بولدین ارزیابی کرد؟ یا باید این روشهای ارزیابی مستقیم به عنوان تابع هدف برای ارزیابی خوشه بندی استفاده بشن؟
سلام و درود،
همانطور که اشاره کردید، شاخصهای ارزیابی درونی، وابسته به معیار اندازهگیری فاصله (شباهت) هستند. در نتیجه برای مثال اگر شاخص دیویس بودلین را با با فاصله اقلیدسی اجرا کنید، برای الگوریتم خوشهبندی k-میانگین به خوبی عمل میکند. متاسفانه ضعفی که این شاخصها دارند، امکان استفاده از آنها را به صورت یک ابزار دقیق و مطلق دچار مشکل میکند. به نظر من بهرهگیری از روش نیمرخ کارایی بهتری دارد.
از اینکه همراه مجله فرادرس هستید سپاسگزارم
شاد و تندرست و پیروز باشید.
سلام. وقت شما بخیر، ممنون از مطالب خوبتون..
ببخشید میشه لطفا معیار ارزیابی و طريقه محاسبه Avg SSQ رو توضیح بدین؟
خیلی ممنون میشم ازتون..
سلام و وقت بخیر.
یکی از روشهای ارزیابی خوشهبندی، پیدا کردن کمترین مربعات درون خوشه است. البته این شیوه بیشتر در زمانی که از فاصله اقلیدسی یا مربع فاصله اقلیدسی (مانند روش k-میانگین) استفاده میکنید استفاده میشود. بنابراین میانگین مربعات فاصله درون گروهی در بین دو شیوه خوشه بندی محاسبه شود، روشی را برتر انتخاب میکنیم که Avg SSQ آن از دیگری کمتر باشد. این کار درست به مانند روش RMSSTD است. منحنی ترسیمی نزولی بوده و اولین مقدار k که کمترین Avg SSQ را داشته باشد به عنوان بهترین مقدار برای تعداد خوشه ها در نظر گرفته شده و ارزیابی خوشه بندی براساس آن صورت می گیرد.
برای توضیحات بیشتر بهتر است مطلب (+) را مطالعه کنید. البته به زودی ترجمه این نوشتار نیز در مجله فرادرس منتشر خواهد شد.
شاد، تندرست و پیروز باشید.
عالی بود – معیار سیلوئت یا نیم رخ یا همان سایه روشن را به بهترین نحو ممکن توضیح دادید.
خیلی خیلی خیلی ممنون
باسلام
يك سوال از خدمتتان داشتم. اگر در خوشه بندي جهت سنجش اعتبار از فواصل درون وبرون خوشه اي استفاده شود، از انجاييكه تمايل داريم فاصله درون خوشه اي كمتر شده و فاصله برون خوشه اي افزايش يابد، اگر فاصله درون خوشه اي براي يك نمونه خوشه بندي كمتر از نمونه دوم ولي فاصله برون خوشه اي نمونه دوم بيشتر از نمونه اول باشد، در اين شايط اولويت تصميم گيري براساس كدام معيار فاصله ايست؟ برون خوشه اي نسبت به درون خوشه اي ااولويت دارد يا برعكس؟
با سلام خدمت شما همراه همیشگی فرادرس.
همانطور که فرمودید، روشهای خوشه بندی براساس کمینهسازی فاصله درون خوشههای و بیشینهسازی فاصله بین خوشهها ساخته میشوند. به همین دلیل در اکثر مواقع برای ارزیابی روش خوشهبندی از هر دو این فاصلهها استفاده میشود. به همین دلیل در شاخصهای معرفی شده در نوشتار روشهای ارزیابی نتایج خوشهبندی (معیارهای درونی) از نسبتیهایی استفاده میشود که در صورت فاصله بین خوشهها و در مخرج فاصله درون خوشه وجود دارد. به این ترتیب روشی که دارای مقدار شاخص بزرگتری است، مناسبتر است (البته در بعضی از موارد مثل شاخص دیویس-بولدین این کسر برعکس است و کوچک بودن این شاخص به معنی مناسبتر بودن شیوه خوشهبندی است).
باز هم از اینکه همراه مجله فرادرس هستید سپاسگزاریم.
موفق، شاد و سلامت باشید.