انواع ویژگی ها (خصیصه ها) و مفهوم بردار ویژگی در داده کاوی
چنانکه پیشتر تشریح شد، مجموعههای داده از نمونهها و ویژگیها (خصیصهها) تشکیل میشوند. یک شی داده نمایانگر یک موجودیت است. برای مثال، در پایگاهداده یک فروشگاه، مشتریان، محصولات موجود و فروشها، اشیا داده هستند. در پایگاهداده پزشکی، بیماران و در پایگاهداده یک دانشگاه، دانشجویان، اساتید و دورهها اشیا داده محسوب میشوند.
به اشیا داده، «نمونه» (sample ،example یا instance)، «نقطه داده» (data points) و یا «شی» (object) نیز میگویند. اگر اشیا داده در پایگاه داده ذخیره شوند، به آنها «تاپلهای داده» (data tuples) گفته میشود. یک تاپل داده در واقع سطری از پایگاه داده است که شامل نقطه داده و ستونهای مربوط به ویژگیهای (خصیصههای) آن میشود. در این مطلب، انواع ویژگیهای موجود مورد بررسی قرار گرفتهاند.
ویژگی چیست؟
یک ویژگی (خصیصه)، فیلد دادهای است که مشخصههای یک شی داده را ارائه میکند. عناوین بُعد و متغیر معمولا در ادبیات این حوزه با معنایی مشابه به کار میروند. اصطلاح بُعد به طور معمول توسط کارشناسان انبار داده مورد استفاده قرار میگیرد. در ادبیات یادگیری ماشین گرایش به استفاده از کلمه ویژگی وجود دارد، در حالیکه آماردانها استفاده از کلمه متغیر را ترجیح میدهند. کارشناسان دادهکاوی و پایگاه داده معمولا از اصطلاح خصیصه استفاده میکنند.
برای مثال، ویژگیهایی که شی «مشتری» را در پایگاه داده یک فروشگاه توصیف میکنند شامل شناسه مشتری (customer ID)، نام (name) و آدرس (address) میشوند. مقادیر مشاهده شده برای یک ویژگی را مشاهدات مینامند.
یک مجموعه از ویژگیها که یک نمونه را توصیف میکنند، بردار ویژگی (feature vector) یا بردار خصیصه (attribute vector) نامیده میشوند. توزیع دادههایی که شامل یک ویژگی (یا متغیر) هستند «تک متغیره» نامیده میشوند. همچنین، توزیعهای «دو متغیره» دارای دو متغیر هستند و به همین صورت به توزیعهای دارای بیش از دو متغیر، «چند متغیره» گفته میشود. نوع یک ویژگی توسط مجموعهای از مقادیر ممکن تعیین میشود. این انواع شامل «اسمی» (nominal) که به آن «دستهای» (categorical) نیز گفته میشود، «دودویی» (binary) و «عددی» (numeric) میشوند. در ادامه هر یک از این انواع تشریح شدهاند.
| انواع ویژگیها | ||
| اسمی (دستهای) ویژگی اسمی ویژگی دودویی (بولین) | ترتیبی
| عددی ویژگی عددی فاصلهای ویژگی عددی نسبتی |
| گسسته یا پیوسته | ||
ویژگیهای اسمی (دستهای)
«اسمی» به معنای «مرتبط با اسامی» است. مقادیر ویژگیهای اسمی نمادها یا اسامی چیزها هستند. هر مقدار حاوی انواع دستهها، کدها یا وضعیتها میشود و بنابراین به این نوع از خصیصهها «دستهای» نیز گفته میشود. مقادیر ویژگیهای دستهای دارای هیچ ترتیب معناداری نیستند. در علوم کامپیوتر، به مقادیر، «شمارنده» (enumerations) نیز گفته میشود.
مثال ۱. ویژگیهای اسمی: رنگ مو و وضعیت تاهل دو ویژگی هستند که شی «شخص» را توصیف میکنند. مقادیر ممکن برای رنگ مو، مشکی، قهوهای، بلوند، طلایی، قرمز، خاکستری و سفید است. خصیصه وضعیت تاهل یکی از مقادیر مجرد، متاهل، مطلقه و بیوه را میپذیرد. رنگ مو و وضعیت تاهل هر دو ویژگیهای اسمی هستند. دیگر مثال از خصیصههای اسمی، حرفه (شغل) با مقادیر معلم، دندانپزشک، برنامهنویس، کشاورز و دیگر موارد است. با اینکه ویژگیهای اسمی، نمادها یا اسامی چیزها هستند، اما این امکان وجود دارد که این اسامی را با مقادیر عددی نیز نمایش داد.
برای مثال، برای رنگ مو میتوان کد رنگ «۰» را به مشکی، «۱» را به قهوهای و به همین صورت سایر اعداد را به دیگر رنگها تخصیص داد. دیگر مثال، شناسه مشتری است که مقادیر ممکن برای آن همه عددی هستند. با این حال، در چنین شرایطی، از اعداد به عنوان مقادیر کمی استفاده نمیشود. به عبارت دیگر، انجام عملیات ریاضی روی دادههای کیفی معنایی ندارد. تفریق کردن شناسه کاربری یک مشتری از شناسه مشتری دیگر (در مقایسه با برای مثال تفریق سن دو فرد از یکدیگر و پیدا کردن اختلاف سنی آنها) هیچ معنایی ندارد.
اگرچه یک مشخصه اسمی ممکن است مقادیر صحیح داشته باشد، اما به عنوان ویژگی عددی در نظر گرفته نخواهد شد زیرا این اعداد صحیح کاربرد کمّی ندارند. به دلیل آنکه مقادیر خصیصههای دستهای دارای هیچ ترتیب معنادار و کمّی نیستند، محاسبه میانگین و میانه برای آنها نیز فاقد معنا است. ولیکن میتوان مُد که یکی از گرایشهای مرکزی و مقداری با بیشترین تکرار در مجموعه داده است را برای چنین ویژگیهایی محاسبه کرد.
ویژگیهای عددی
یک ویژگی عددی، خصیصهای کمّی است که با استفاده از مقادیر صحیح یا حقیقی نمایش داده میشود. متغیرهای عددی میتوانند از نوع فاصلهای یا نسبتی باشند.
ویژگیهای عددی فاصلهای
خصیصههای عددی فاصلهای بر اساس مقیاس واحدهایی با اندازه برابر اندازهگیری میشوند. مقادیر ویژگیهای عددی دارای ترتیب هستند و میتوانند مثبت، صفر و یا منفی باشند. بدین ترتیب، علاوه بر فراهم کردن مقادیر دارای رتبهبندی، چنین خصیصههایی به کاربران امکان مقایسه و کمیسازی تفاوت بین مقادیر را میدهد.
مثال ۲. ویژگیهای عددی فاصلهای: خصیصه دما نوعی ویژگی فاصلهای است. مجموعه داده دمای هوا برای تعدادی از روزهای گوناگون که در آن هر روز یک شی داده محسوب میشود، مفروض است. با مرتبسازی مقادیر، رتبهبندی اشیا با در نظر گرفتن دما حاصل خواهد شد. به علاوه، میتوان تفاوت بین مقادیر را کمیسازی کرد. برای مثال، دما ۲۰، پنج درجه بیشتر از ۱۵ است.
تاریخهای تقویم مثال دیگری از خصیصههای عددی فاصلهای هستند. برای مثال سال ۲۰۰۲ و ۲۰۱۰ هشت سال با یکدیگر اختلاف دارند. دما به سلسیوس و فارنهایت هیچ نقطه صفر واقعی ندارد، در واقع نه ◦۰ سلسیوس و نه ◦۰ فارنهایت، هیچ کدام به معنای «نبود دما» نیست (در مقیاس سلسیوس، واحد اندازهگیری از ۱ تا ۱۰۰ تفاوت بین دمای ذوب و جوش آب در فشار جو است).
اگرچه میتوان تفاوت بین مقادیر دما را محاسبه کرد، اما نمیتوان گفت یک درجه حرارت چه نسبتی با دیگری دارد زیرا هیچ صفر مطلقی وجود ندارد. در واقع نمیتوان گفت دمای ◦۱۰ سلسیوس دو برابر گرمتر از ◦۵ سلسیوس است. به طور مشابه، هیچ صفر مطلقی برای تاریخهای تقویم وجود ندارد (سال صفر آغاز زمان نبوده است)، و این موجب میشود زمان نیز خصیصهای نسبی نباشد. از آنجا که خصیصههای فاصلهای عددی هستند، میتوان مقدار میانگین، میانه و مُد را که از گرایشهای مرکزی هستند اندازهگیری کرد.
ویژگیهای نسبتی
یک ویژگی نسبتی یک خصیصه عددی با یک صفر مطلق است. اگر اندازهها نسبتی باشند، میتوان از نسبت مقادیر با یکدیگر سخن گفت. به علاوه، مقادیر قابل مرتبسازی شدن هستند و میتوان تفاضل بین آنها، میانگین، میانه و مُد را محاسبه کرد.
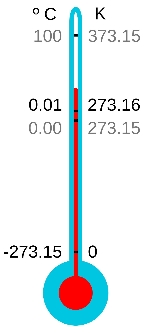
مثال ۳. ویژگیهای نسبتی. بر خلاف درجه حرارت سلسیوس و فارنهایت، درجه حرارت کلوین آنچه را که صفر مطلق محسوب میشود در بر دارد (◦۰ کلوین = - ◦۲۷۳ سلسیوس). در دمای صفر کلوین، انرژی جنبشی ذرات سازنده به کمینه خود میرسد و آنتروپی و آنتالپی صفر میشود. از جمله دیگر مثالهایی که میتوان برای ویژگیهای نسبتی به آن اشاره کرد، خصیصههای شمارشی مانند سالهای تجربه (برای مثال اشیا داده کارمندان هستند) و تعداد کلمات (برای مثال در شی دادهای مانند اسناد چاپی) هستند. مثالهای دیگر عبارتند از اندازه وزن، ارتفاع، طول و عرض جغرافیایی و کمیتهای پولی (برای مثال فردی با ۱۰۰ دلار پول، ۱۰۰ برابر پولدارتر از فردی با ۱ دلار است).
ویژگیهای گسسته و پیوسته
همانطور که پیش از این بیان شد، ویژگیها در دستههای اسمی، دودویی، ترتیبی و عددی قرار دارند. راههای زیادی برای سازماندهی انواع خصیصهها وجود دارد. این انواع دو به دو ناسازگار نیستند. الگوریتمهای دستهبندی از زمینهای از یادگیری ماشین توسعه یافتهاند که اغلب درباره ویژگیهای گسسته یا پیوسته سخن میگویند. هر نوع ویژگی (گسسته و پیوسته) ممکن است به طور متفاوتی پردازش شود. یک خصیصه گسسته مجموعهای متناهی یا نامتناهی (غیر قابل شمارش) از مقادیر است که میتواند به صورت صحیح باشد یا نباشد.
متغیرهای رنگ مو، سیگاری بودن یا نبودن، تستهای پزشکی و تعداد بطریهای نوشیدنی دارای مقادیر متناهی هستند و بنابراین گسسته محسوب میشوند. لازم به ذکر است که خصیصههای متناهی ممکن است مقادیر عددی مانند ۰ و ۱ را برای ویژگیهای دودویی و یا ۰ الی ۱۲۰ را برای خصیصه سن داشته باشند. یک خصیصه به لحاظ شمارشی نامتناهی محسوب میشود اگر مجموعه مقادیر ممکن برای آن نامتناهی باشد. اما این مقادیر را میتوان در یک تناظر یک به یک با مجموعه اعداد طبیعی قرار داد. برای مثال، خصیصه شناسه مشتری (customer_ID) به لحاظ شمارشی نامتناهی است.
تعداد مشتریان میتواند به طور نامتناهی رشد کند، اما در حقیقت مجموعه واقعی از مقادیر قابل شمارش است. کدهای پستی نمونه دیگری از این مورد هستند. اگر مقادیر یک ویژگی گسسته نباشد، پیوسته است. اصطلاح خصیصه عددی و پیوسته معمولا در ادبیات به جای یکدیگر به کار میروند (این امر میتواند گیج کننده باشد زیرا در تصور کلاسیک، مقادیر پیوسته اعداد حقیقی هستند که در آنها مقادیر میتوانند صحیح یا حقیقی باشد). در عمل، اعداد حقیقی با استفاده از تعداد متناهی از ارقام ارائه میشوند. خصیصههای پیوسته معمولا متغیرهای شناور هستند.
اگر نوشته بالا برای شما مفید بود، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای هوش محاسباتی
- مدلسازی، برازش و تخمین
- آموزش انواع داده در متلب – (رایگان)
- گنجینه آموزشهای برنامهنویسی کاربردی متلب — از مقدماتی تا پیشرفته
- جامعه آماری — انواع داده و مقیاسهای آنها
^^











ممنونم،برای من مطلب خیلی بسیارمفیدی بود
بسیارممنونم خیلی مفیدی بود