مساحت هرم و محاسبه آن — به زبان ساده

مساحت هرم برابر حاصل جمع مساحت قاعده و مساحت وجههای جانبی این شکل سه بعدی است. مساحت قاعده هرم با توجه به شکل هندسی آن (مثلث، مربع و غیره) تعیین میشود. به عنوان مثال، اگر قاعده به شکل مربع باشد، مساحت آن برابر طول یک ضلع ضربدر خودش خواهد بود. محاسبه مساحت وجههای جانبی نیز با استفاده از محیط قاعده و ارتفاع (در هرمهای منتظم) یا جمع مساحت وجهها (در هرمهای غیر منتظم) انجام میگیرد. در این مقاله، فرمول و نحوه محاسبه مساحت هرم های مختلف را به همراه چندین مثال متنوع آموزش میدهیم.
انواع حجم های هندسی چه هستند؟
حجم های هندسی به سه دسته اصلی منشوری، کروی و هرمی تقسیم میشوند. برخی از حجمهای هندسی، ترکیبی از این سه نوع هستند. تصویر زیر، دو مثال از حجمهای هرمی با عنوان هرم و مخروط را نمایش میدهد.

هرم چیست ؟
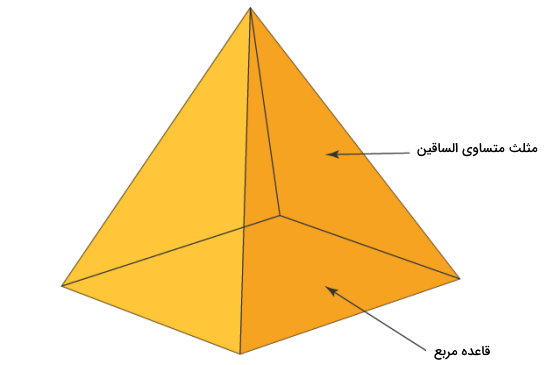
هرم، یک شکل هندسی سه بعدی است که از اتصال چند ضلعیهای دو بعدی به یکدیگر تشکیل میشود. تصویر زیر، ساختار کلی یکی از انواع هرم را نمایش میدهد.

اجزای هرم چه هستند ؟
هرمها از سه جز اصلی راس، وجه و قاعده تشکیل میشوند. این اجزا، به منظور تعیین مساحت و حجم هرم مورد استفاده قرار میگیرند.
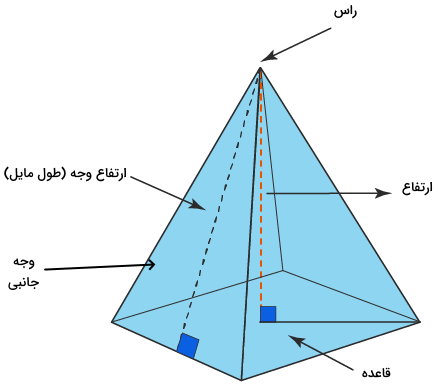
تعریف هر یک از اجزای هرم عبارت است از:
- قاعده هرم: به پایینترین وجه هرم، قاعده میگویند. قاعده هرم از یک چند ضلعی صاف است که وجههای دیگر هرم به آن متصل میشوند. مثلث و مربع، از شکلهای رایج برای تشکیل قاعده هرم هستند.
- وجه جانبی هرم: به چند ضلعیهای قرار گرفته بر روی اضلاع قاعده، وجه هرم میگویند. تمام وجههای هرم، همیشه به شکل مثلث هستند.
- راس هرم: محل تقاطع وجههای هرم، با عنوان راس شناخته میشود. راس هرم، نقطه مشترک تمام وجهها است.
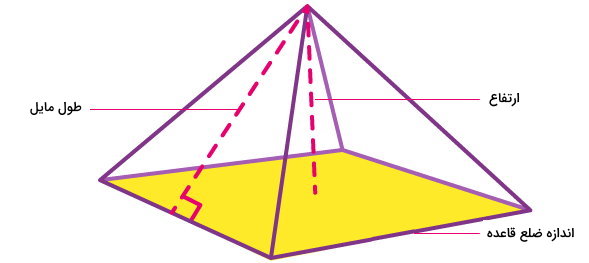
- ارتفاع هرم: به فاصله عمودی راس تا قاعده، ارتفاع هرم میگویند.
- ارتفاع وجه: به فاصله عمودی راس تا قاعده هر وجه، ارتفاع وجه جانبی یا طول مایل گفته میشود.
انواع هرم کدام هستند ؟
هرمها بر اساس معیارهایی نظیر شکل قاعده، زاویه ارتفاع و اندازه ضلعهای قاعده به انواع زیر تقسیم میشوند:
- انواع هرم بر اساس چند ضلعی قاعده
- هرم با قاعده مثلث (سه ضلعی)
- هرم با قاعده مربع (چهار ضلعی)
- هرم با قاعده پنج ضلعی
- و غیره
- انواع هرم بر اساس زاویه بین ارتفاع و قاعده
- هرم عمود یا هرم قائم
- هرم مایل
- انواع هرم بر اساس اندازه ضلعهای قاعده
- هرم منتظم
- هرم غیر منتظم
محاسبه مساحت هر یک از انواع هرم، دارای روش خاصی است که در بخشهای بعدی به توضیح برخی از آنها خواهیم پرداخت.
مساحت هرم چیست ؟
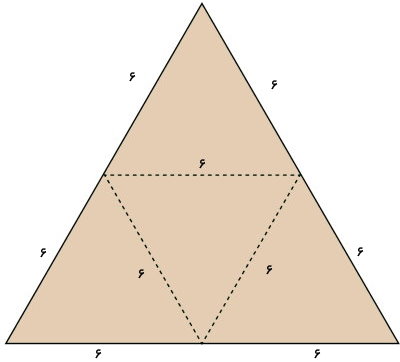
مساحت هرم، اندازه سطح تمام وجههای آن (سطح وجههای جانبی و قاعده) است. به منظور درک مفهوم مساحت هرم، شکل زیر را در نظر بگیرید. این شکل، یک هرم با قاعده مثلث متساوی الاضلاع را نمایش میدهد.

اگر وجههای این هرم را باز کنیم، شکل زیر به وجود میآید. به این شکل، گسترده هرم میگویند. گسترده هرم، نمایش دو بعدی هر یک از وجههای این شکل سه بعدی است.
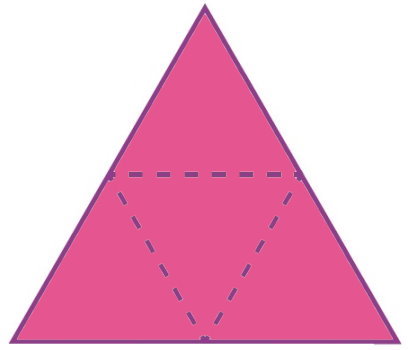
مساحت هرم، با جمع مساحتهای بخشهای مختلف گسترده آن محاسبه میشود. در تصویر بالا، مساحت هرم، مجموع مساحت چهار مثلث تشکیل دهنده آن خواهد بود. اگر قاعده هرم شکل دیگری باشد، مساحت هرم از جمع مساحت قاعده با مساحت مثلثهای جانبی به دست میآید.
فرمول مساحت هرم چیست ؟
مساحت هرم با استفاده از رابطه کلی زیر محاسبه میشود:
$$
TSA = BSA + LSA
$$
- TSA: مساحت هرم
- BSA: مساحت قاعده
- LSA: مساحت وجههای جانبی
مثال 1: تعیین مساحت هرم مثلث متساوی الاضلاع
تصویر زیر، یک جسم هرمی با قاعده مثلث متساوی الاضلاع را نمایش میدهد. اگر وجههای این هرم نیز به شکل مثلث متساوی الاضلاع باشند، اندازه ضلعها و مساحت هرم چقدر است؟ (اندازه ضلع قاعده هرم را برابر 6 سانتیمتر در نظر بگیرید.)

به منظور درک بهتر نحوه حل این مثال، ابتدا گسترده هرم بالا را رسم میکنیم و اندازه ضلعهای تمام وجههای آن را به دست میآوریم. از آنجایی که هر چهار وجه هرم، مثلثهای متساوی الاضلاع هستند، گسترده هرم مانند تصویر زیر میشود.
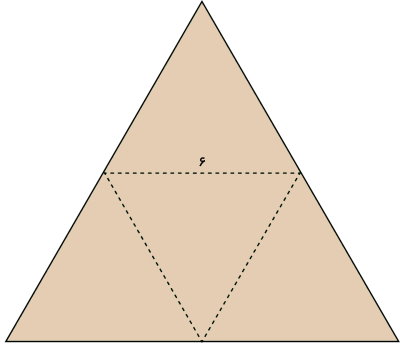
اندازه یک ضلع قاعده برابر 6 سانتیمتر است. بنابراین، اندازه تمام ضلعها برابر با 6 خواهد بود.
مساحت هرم، از رابطه زیر به دست میآید:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم
قاعده هرم، یک مثلث متساوی الاضلاع است. فرمول مساحت مثلث متساوی الاضلاع به صورت زیر نوشته میشود:
$$
A = \frac { \sqrt {3} } {4} a^2
$$
- A: مساحت مثلث متساوی الاضلاع
- a: اندازه ضلع مثلث متساوی الاضلاع برابر 6
اندازه ضلع را درون فرمول قرار میدهیم و آن را حل میکنیم:
$$
A = \frac { \sqrt {3} } {4} \times 6^2
$$
$$
A = \frac { \sqrt {3} } {4} \times 36
$$
$$
A = \sqrt {3} \times 9
$$
مساحت قاعده برابر $$9\sqrt {3}$$ است. بنابراین، مساحت هر یک از وجههای هرم نیز برابر با $$9\sqrt {3}$$ خواهد بود. به این ترتیب، مساحت هرم به صورت زیر محاسبه میشود:
$$9\sqrt {3} + (9\sqrt {3} + 9\sqrt {3} + 9\sqrt {3})$$ = مساحت هرم
$$
4 \times (9\sqrt {3})
$$
$$
36\sqrt {3}
$$
به هرم مورد بررسی در این مثال، یک هرم منتظم گفته میشود. مساحت هرمهای منتظم، فرمول مختص به خود را دارد که در بخش بعدی به معرفی و حل مثالهای مرتبط با آن میپردازیم.
مساحت هرم منتظم چگونه بدست می آید؟
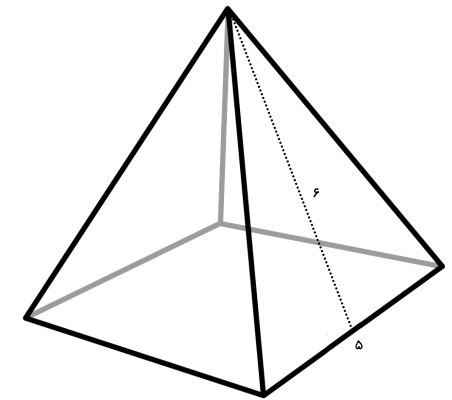
به هرمی که قاعده آن یک چند ضلعی منتظم (مثلث متساوی الاضلاع، مربع و غیره) باشد، هرم منتظم میگویند. اندازه ضلعها و زاویههای قاعده هرم منتظم، مساوی هستند. این ویژگی، باعث برابری تمام وجههای این نوع هرم میشود. هرم زیر را در نظر بگیرید.
قاعده هرم نمایش داده شده در تصویر بالا، یک مربع است. مربع، از چهار ضلع مساوی و چهار زاویه قائمه تشکیل میشود. وجههای هرم، چهار مثلث متساوی الساقین هستند. این مثلث، از دو ضلع مساوی تشکیل میشود. در هرمهای منتظم، وجههای جانبی همیشه به شکل مثلث متساوی الساقین خواهند بود. به این ترتیب، مساحت هرم منتظم از رابطه زیر به دست میآید:
مساحت مثلثهای متساوی الساقین + مساحت قاعده = مساحت هرم منتظم
مساحت قاعده هرم، به شکل قاعده بستگی دارد. به عنوان مثال، اگر قاعده به شکل مربع باشد، مساحت آن با ضرب یک ضلع در خود تعیین میشود. محاسبه مساحت مثلث متساوی الساقین نیز با استفاده از اندازه قاعده و ارتفاع نظیر انجام میگیرد.
یکی از نکات مهم در محاسبه اجزای هرمهای منتظم، این است که ارتفاع وجه جانبی، همیشه در مرکز ضلع قاعده و ارتفاع هرم، همیشه در مرکز قاعده قرار میگیرد. این ویژگی میتواند به تعیین اندازههای مختلف هرم کمک کند.
فرمول مساحت هرم منتظم چیست ؟
فرمول مساحت هرم منتظم بر اساس طول مایل و اندازه ضلع قاعده عبارت است از:
$$
TSA = \frac {P \times s} {2}+B
$$
- TSA: مساحت هرم
- P: محیط قاعده هرم
- s: طول مایل یا ارتفاع وجه جانبی
- B: مساحت قاعده هرم
عبارت اول فرمول بالا، مساحت تمام وجههای جانبی را نمایش میدهد:
$$
LSA = \frac {P \times s} {2}
$$
- Sl: مساحت سطح جانبی هرم
- P: محیط قاعده هرم
- s: طول مایل یا ارتفاع وجه جانبی
فرمول مساحت وجههای جانبی، شباهت زیادی به فرمول مساحت مثلث دارد. فقط به جای قاعده مثلث، از محیط قاعده هرم در آن استفاده شده است؛ چراکه جمع قاعده تمام وجهها (تمام ضلعهای قاعده هرم)، برابر با محیط قاعده هرم خواهد بود. فرمولهای بالا، برای تمام هرمهای منتظم قابل استفاده هستند. از اینرو، برای استفاده از آنها، باید با نحوه محاسبه محیط و مساحت چند ضلعیهای منتظم آشنا باشید.
مثال 2: تعیین مساحت هرم با قاعده مربع
مساحت هرم مربعی زیر را حساب کنید.
مطابق با فرمول مساحت هرم منتظم، داریم:
$$
TSA = \frac {P \times s} {2}+B
$$
- TSA: مساحت هرم
- P: محیط قاعده هرم
- s: طول مایل یا ارتفاع وجه جانبی برابر 6
- B: مساحت قاعده هرم
محیط قاعده، همان محیط مربع است که با استفاده از فرمول زیر محاسبه میشود:
$$
P = 4 \times a
$$
- P: محیط مربع
- a: طول ضلع مربع برابر 5
$$
P = 4 \times 5
$$
$$
P = 20
$$
مساحت قاعده، همان مساحت مربع است که از طریق رابطه زیر به دست میآید:
$$
B = a \times a
$$
$$
B = a ^ { 2 }
$$
- B: مساحت مربع
- a: اندازه ضلع مربع برابر 5
$$
B = 5 ^ { 2 }
$$
$$
B = 25
$$
اکنون، مقادیر محیط قاعده (24)، مساحت قاعده (36) و طول مایل (5) را درون فرمول مساحت هرم منتظم قرار میدهیم و آن را حل میکنیم:
$$
TSA = \frac {20 \times 6} {2}+25
$$
$$
TSA = \frac {120} {2}+25
$$
$$
TSA = 60+25
$$
$$
TSA = 85
$$
در نتیجه، مساحت هرم منتظم با قاعده مربع برابر 85 است.
مساحت هرم غیر منتظم چگونه بدست می آید ؟
به هرمی که قاعده آن منتظم نباشد، هرم غیر منتظم یا نامنتظم گفته میشود. اصول تعیین مساحت هرمهای غیر منتظم و منتظم، هیچ تفاوتی با یکدیگر ندارد. در هر دو مورد، این مساحت از جمع مساحت قاعده و مساحت وجههای جانبی به دست میآید. تصویر زیر، نمونهای از یک هرم غیر منتظم را نمایش میدهد.
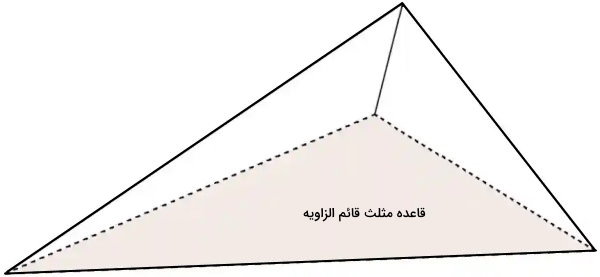
قاعده هرم بالا، به شکل مثلث قائم الزاویه است. به دلیل برابر نبودن اندازه تمام ضلعها و تمام زاویههای مثلث قائم الزاویه، این هرم، به عنوان یک هرم غیر منتظم در نظر گرفته میشود. مساحت قاعده هرم بالا، با استفاده از فرمولهای مساحت مثلث قائم الزاویه به دست میآید. با این حال، تا زمانی که طول مایل هر یک از وجههای جانبی مشخص نباشد، امکان تعیین مساحت هرم وجود ندارد.
فرمول مساحت هرم غیر منتظم چیست ؟
فرمول مساحت هرم غیر منتظم، همان فرمول کلی مساحت هرمها است:
$$
TSA = BSA + LSA
$$
- TSA: مساحت هرم غیر منتظم
- BSA: مساحت قاعده
- LSA: مساحت وجههای جانبی
مساحت هرم ناقص چگونه بدست می آید ؟
اگر قسمت بالایی هرم را توسط صفحه موازی با قاعده آن جدا کنیم، یک شکل هندسی با عنوان هرم ناقص یا «بریده هرمی» (Pyramid Frustum) تشکیل میشود. تصویر زیر، یک هرم ناقص با قاعده چهار ضلعی را نمایش میدهد.
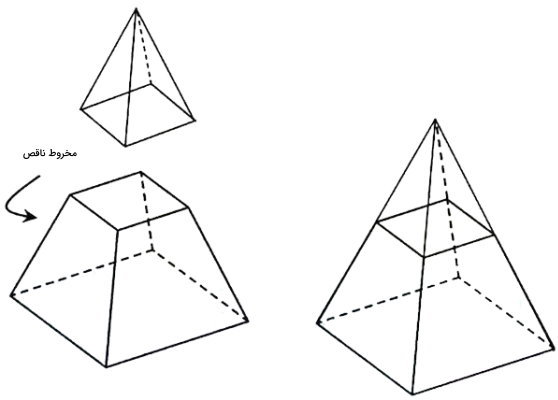
در هرم ناقص، به جای یک راس و یک قاعده، دو قاعده وجود دارد. به این ترتیب، مساحت این شکل هندسی، از جمع مساحت دو قاعده با مساحت وجههای جانبی به دست میآید. وجههای جانبی هرم ناقص، به شکل ذوزنقه هستند. از اینرو، به منظور تعیین مساحت آنها باید از فرمول محاسبه مساحت ذوزنقه استفاده کرد. محاسبه مساحت قاعدهها نیز بر اساس نوع چند ضلعی انجام میگیرد.
فرمول مساحت هرم ناقص چیست ؟
فرمول محاسبه مساحت هرم ناقص به صورت زیر نوشته میشود:
$$
TSA = BSA + LSA
$$
- TSA: مساحت هرم ناقص
- BSA: مساحت قاعدهها
- LSA: مساحت وجههای جانبی
مساحت قاعدههای هرم ناقص به شکل قاعده بستگی دارد. فرمول این مساحت برای برخی از شکلهای متداول در جدول زیر آورده شده است.
| شکل قاعده | فرمول مساحت قاعده | اندازهها |
| مثلث | $$ \frac {b \times h} {2} $$ | b، قاعده مثلث و h، ارتفاع مثلث |
| مربع | $$ a \times a $$ | a، اندازه یک ضلع |
| مستطیل | $$ l \times w $$ | l، طول و w، عرض |
| لوزی | $$ p \times q $$ | p و q، قطرهای لوزی |
| ذوزنقه | $$ \frac{a+b}{2} h $$ | a و b، قاعدهها و h، ارتفاع ذوزنقه |
| متوازی الاضلاع | $$ b \times h $$ | b، قاعده و h، ارتفاع |
مساحت وجههای هرم ناقص با استفاده از فرمول مساحت ذوزنقه به دست میآید. این فرمول به صورت زیر نوشته میشود:
$$
A=\frac{a+b}{2} h
$$
- A: مساحت ذوزنقه
- a: یکی از قاعدههای ذوزنقه
- b: قاعده دیگر ذوزنقه
- h: ارتفاع
به این ترتیب، مساحت هر وجه به دست میآید. جمع این مساحتها، مساحت وجههای جانبی هرم ناقص است. البته در صورتی که اندازه ضلعهای قاعدهها و ارتفاع مایل هرم ناقص مشخص باشد، نیازی به استفاده از فرمول بالا و جمع مساحتهای تمام وجهها نخواهد بود. در این حالت، فرمول زیر به منظور تعیین مساحت وجههای جانبی هرم ناقص مورد استفاده قرار میگیرد:
$$
LSA = \frac {P_1 + P_2} {2} \times h
$$
- LSA: مساحت وجههای جانبی هرم ناقص
- P1: محیط یکی از قاعدهها
- P2: محیط قاعده دیگر
- s: ارتفاع مایل
به طور کلی، فرمول مساحت هرم نقص را میتوان به فرم زیر نوشت:
$$
TSA = B_1 + B_2 + (\frac {P_1 + P_2} {2} \times s)
$$
- TSA: مساحت هرم ناقص
- B1: مساحت قاعده اول
- B2: مساحت قاعده دوم
- P1: محیط قاعده اول
- P2: محیط قاعده دوم
- s: ارتفاع وجه (طول مایل)
به منظور آشنایی با فرمولهای محیط و مساحت اشکال مختلف هندسی، مطالعه مطلب «فرمول های محیط و مساحت اشکال هندسی (+ فیلم و PDF رایگان)» را به شما پیشنهاد میکنیم.
مثال 3: محاسبه مساحت هرم ناقص
مساحت هرم ناقص مربعی زیر را حساب کنید. (ارتفاع مایل را برابر 12 در نظر بگیرید.)
محاسبه مساحت جانبی هرم ناقص استفاده از فرمول زیر انجام میشود:
$$
TSA = B_1 + B_2 + (\frac {P_1 + P_2} {2} \times h)
$$
- TSA: مساحت هرم ناقص
- B1: مساحت قاعده اول
- B2: مساحت قاعده دوم
- P1: محیط قاعده اول
- P2: محیط قاعده دوم
- s: ارتفاع وجه (طول مایل) برابر 12
مساحت قاعده اول از رابطه مساحت مربع به دست میآید:
$$
B_1 = 10 \times 10
$$
$$
B_1 = 100
$$
به همین صورت، مساحت قاعده دو برابر است با:
$$
B_2 = 7 \times 7
$$
$$
B_2 = 49
$$
بر اساس فرمول محیط مربع، برای محیط قاعده اول داریم:
$$
P_1 = 4 \times 10
$$
$$
P_1 = 40
$$
محیط قاعده دوم نیز به همین صورت به دست میآید:
$$
P_2 = 4 \times 7
$$
$$
P_2 = 28
$$
اندازههای به دست آمده را به همراه طول مایل در فرمول محاسبه مساحت هرم ناقص قرار میدهیم و آن را حل میکنیم:
$$
TSA = 100 + 49 + (\frac {40 + 28} {2} \times 12)
$$
$$
TSA = 149 + (\frac {68} {2} \times 12)
$$
$$
TSA = 149 + (34 \times 12)
$$
$$
TSA = 149 + (408)
$$
$$
TSA = 149 + (\frac {68} {2} \times 12)
$$
$$
TSA = 557
$$
مساحت هرم ناقص برابر 557 است.
مساحت هرم با قاعده مثلث
هرم مثلثی هرم با قاعده مثلث، از چهار وجه به شکل مثلث تشکیل میشود. اگر قاعده، یک مثلث متساوی الاضلاع باشد، هرم از نوع منتظم خواهد بود. تصویر زیر، یک هرم مثلثی منتظم را نمایش میدهد.
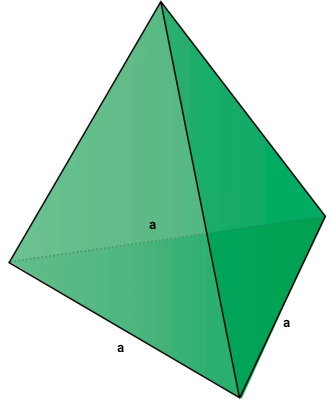
مساحت هرم مثلثی (منتظم یا غیر منتظم) نیز مانند تمام انواع هرم، از جمع مساحت وجههای تشکیل دهنده آن به دست میآید. به این ترتیب، رابطه مساحت هرم با قاعده مثلث به صورت زیر نوشته میشود:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم مثلثی
$$
TSA = BSA + LSA
$$
- TSA: مساحت هرم
- BSA: مساحت قاعده
- LSA: مساحت وجههای جانبی
به منظور تعیین مساحت قاعده میتوان از فرمول مساحت مثلث استفاده کرد:
$$
A = \frac {b \times h} {2}
$$
- A: مساحت مثلث
- b: قاعده مثلث (اندازه یکی از ضلعها)
- h: ارتفاع نظیر قاعده
البته اگر قاعده از نوع مثلث متساوی الاضلاع باشد، مساحت آن از فرمول زیر به دست میآید:
$$
A=\frac{\sqrt{3}}{4} a^{2}
$$
- A: مساحت مثلث متساوی الاضلاع
- a: اندازه یک ضلع مثلث
روش محاسبه مساحت وجههای جانبی هرم مثلثی نیز به اندازههای معلوم و نوع هرم بستگی دارد. اگر هرم از نوع منتظم بوده و ارتفاع وجه جانبی (طول مایل) داده شده باشد، رابطه زیر، به منظور تعیین مساحت هر سه وجه جانبی مورد استفاده قرار میگیرد:
$$
LSA = \frac {P \times s} {2}
$$
- LSA: مساحت وجههای جانبی
- P: محیط قاعده هرم (محیط مثلث متساوی الاضلاع برابر 3a است.)
- s: طول مایل
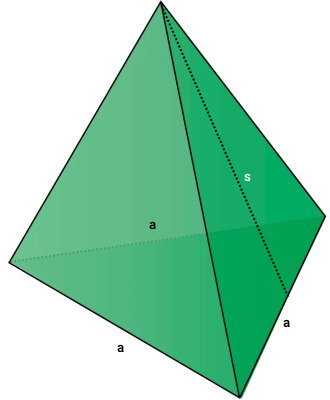
اگر هرم مثلثی، از نوع غیر منتظم باشد، باید مساحت تمام وجههای جانبی را به صورت جداگانه محاسبه و با یکدیگر جمع کرد. این محاسبات، نیازمند اندازه طول مایل هر سه وجه جانبی است. به طور کلی، فرمول مساحت هرم منتظم با قاعده مثلث به صورت زیر نوشته میشود:
$$
TSA = (\frac{\sqrt{3}}{4} a^{2} )+ (\frac{3a \times s} {2})
$$
- TSA: مساحت هرم مثلثی منتظم
- a: اندازه ضلع مثلث متساوی الاضلاع
- s: طول مایل
علاوه بر فرمول بالا، یک فرمول دیگر نیز وجود دارد که مساحت هرم مثلثی را بر اساس اندازه ضلع وجههای جانبی و ارتفاع هرم محاسبه میکند. این فرمول عبارت است از:
$$
TSA = (\frac{a \times b}{2} )+ (\frac{3 \times b \times s} {2})
$$
- TSA: مساحت هرم مثلثی منتظم
- a: ارتفاع هرم
- b: اندازه ضلع هر وجه جانبی
- s: طول مایل
مثال 4: محاسبه مساحت هرم با قاعده مثلث
اگر اندازه تمام ضلعهای قاعده هرم زیر مساوی باشد، مساحت هرم چقدر خواهد بود؟ (رادیکال 3 را برابر 1/7 در نظر بگیرید.)
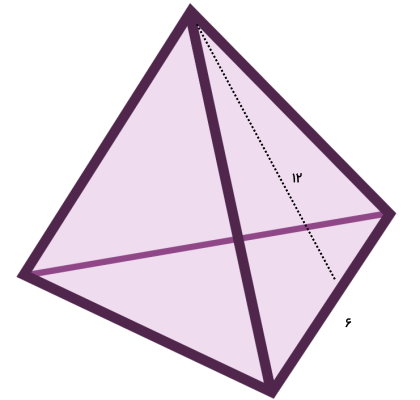
بر اساس فرمول مساحت هرم منتظم با قاعده مثلث داریم:
$$
TSA = (\frac{\sqrt{3}}{4} a^{2} )+ (\frac{3a \times s} {2})
$$
- TSA: مساحت هرم مثلثی منتظم
- a: اندازه ضلع قاعده برابر 6
- s: طول مایل برابر 12
اندازههای معلوم را درون فرمول بالا قرار میدهیم و آن را حل میکنیم:
$$
TSA = (\frac{\sqrt{3}}{4} \times 6^{2} )+ (\frac{3 \times 6 \times 12} {2})
$$
$$
TSA = (\frac{\sqrt{3}}{4} \times 36 )+ (\frac{216} {2})
$$
$$
TSA = (9\sqrt{3} )+ (108)
$$
$$
TSA = (9\times 1.7 )+ (108)
$$
$$
TSA = (15.3 )+ (108)
$$
$$
TSA = 123.3
$$
در نتیجه، مساحت هرم مثلثی برابر 123/3 است.
مساحت هرم با قاعده مستطیل
هرم مستطیلی، یکی دیگر از انواع هرم با قاعده چهار ضلعی است. در بخش محاسبه مساحت هرم منتظم، به معرفی هرم با قاعده مربع پرداختیم. در هرم با قاعده مستطیل، وجههای جانبی به صورت دو به دو با هم برابر هستند. تصویر زیر، هرم مستطیلی به ارتفاع h، طول قاعده l و عرض w را نمایش میدهد.
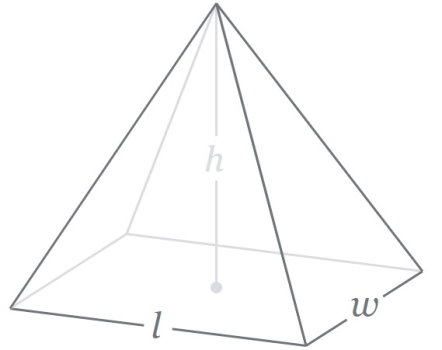
فرمول مخصوص مساحت هرم با قاعده مستطیل به صورت زیر نوشته میشود:
$$
TSA=l w+l \sqrt{\left(\frac{w}{2}\right)^{2}+h^{2}}+w \sqrt{\left(\frac{l}{2}\right)^{2}+h^{2}}
$$
- TSA: مساحت هرم مستطیلی
- l: طول قاعده هرم (طول مستطیل)
- w: عرض قاعده هرم (عرض مستطیل)
- h: ارتفاع هرم
فرمول مساحت هرم مربعی
مربع، یکی از انواع خاص مستطیل است. بر اساس فرمول مساحت هرم مستطیلی، میتوان فرمول مساحت هرم با قاعده را به صورت زیر نوشت:
$$
TSA=a^{2}+2 a \sqrt{\frac{a^{2}}{4}+h^{2}}
$$
- TSA: مساحت هرم مربعی
- a: اندازه ضلع قاعده (ضلع مربع)
- h: ارتفاع هرم
در بخشهای بعدی، چند مثال در رابطه محاسبه مساحت هرمهای مستطیلی و مربعی حل میکنیم.
محاسبه آنلاین مساحت هرم
از سایتهای اینترنتی کاربردی برای محاسبه مساحت هرم میتوان به سایت Blocklayer (+) و موتور جستجوی گوگل اشاره کرد. با جستجوی عبارت «pyramid area» در سایت گوگل، کادری مشابه تصویر زیر در بالای صفحه نتایج به نمایش در میآید.
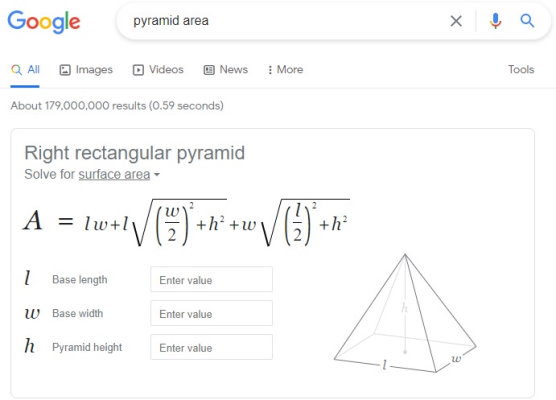
هرم نمایش داده شده در صفحه نتایج گوگل دارای قاعده مستطیلی است. با وارد کردن طول قاعده هرم در کادر مقابل عنوان «l Base length»، عرض قاعده هرم در کادر مقابل عنوان «w Base width» و ارتفاع هرم در کادر مقابل عنوان «h Pyramid height»، مساحت هرم محاسبه شده و نتیجه آن به همراه روند حل نشان داده میشود.
یکی دیگر از ابزارهای آنلاین و کاربردی در زمینه محاسبه مساحت هرم، ماشین حساب هرم در سایت Blocklayer (+) است. بر خلاف اشین حساب گوگل، این ماشین حساب از قابلیتهای بیشتری برای تعریف انواع مختلف قاعده و امکان تنظیم زاویه وجهها بهره میبرد. البته کار کردن با ماشین حساب هرم Blocklayer پیچیدهتر است. تصویر زیر، بخش کوچکی از صفحه ورودیها و خروجیهای این ابزار را نمایش میدهد.

ویژگی جالب ماشین حساب هرم Blocklayer، نمایش تصویری تمام بخشهای هرم (تصویر از بالا، تصویر از رو به رو) و امکان تنظیم اغلب متغیرها (ارتفاع، زاویه، شکل قاعده و غیره) است. این ابزار، علاوه بر محاسبه حجم و دیگر پارامترهای مرتبط، امکان چاپ گسترده هرم برای ساخت مدل واقعی را نیز فراهم میکند.
مثال 5: محاسبه مساحت هرم مربعی با گوگل
یک هرم مربعی شکل را در نظر بگیرید. اگر اندازه ضلع قاعده هرم برابر 16 سانتیمتر و ارتفاع هرم برابر 15 سانتیمتر باشد، مساحت هرم چقدر خواهد بود؟
به منظور حل این مثال، از ماشین حساب هرم گوگل کمک میگیریم. به این منظور، عنوان «pyramid area» را در سایت گوگل جستجو میکنیم تا کادر محاسبه مساحت هرم به نمایش درآید. سپس، عدد 16 را در کادر l (طول قاعده)، عدد 16 را در کادر w (عرض قاعده) و عدد 15 را در کادر h (ارتفاع هرم) وارد میکنیم.
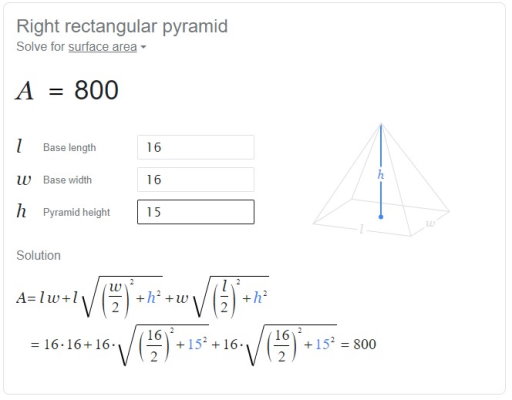
با تایپ آخرین عدد، مساحت هرم محاسبه شده و نتیجه آن به همراه مراحل حل به نمایش در میآید. بر اساس تصویر بالا، مساحت هرم برابر 800 سانتیمتر مربع است.
حل مثال های مساحت انواع هرم
برای آشنایی بیشتر با نحوه محاسبه مساحت انواع هرم، در این بخش، به حل چندین مثال میپردازیم.
مثال 6: محاسبه مساحت گسترده هرم مثلثی
قاعده هرم نمایش داده شده در تصویر زیر، مثلث متساوی الاضلاع به ضلع 5 است. اگر طول مایل وجههای جانبی برابر 10 باشد، مساحت گسترده هرم چقدر خواهد بود؟
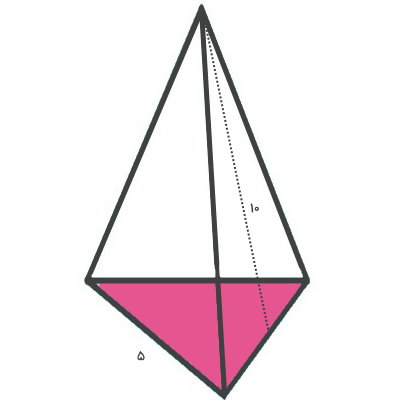
گسترده یک هرم، نمایش دو بعدی قاعده و وجههای جانبی آن در کنار یکدیگر است. گسترده هرم بالا، مشابه تصویر زیر رسم میشود.
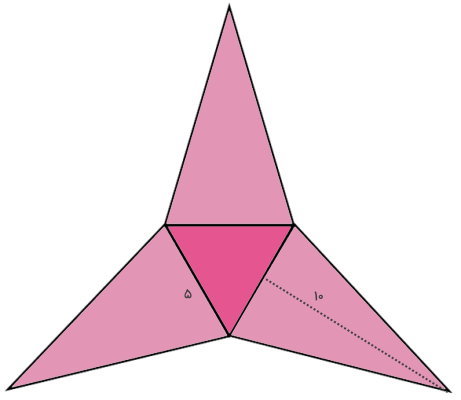
مساحت گسترده هرم، برابر مساحت قاعده و تمام وجههای آن است. به منظور محاسبه مساحت قاعده، از فرمول مساحت مثلث متساوی الاضلاع استفاده میکنیم:
$$
A=\frac{\sqrt{3}}{4} a^{2}
$$
- A: مساحت مثلث متساوی الاضلاع
- a: اندازه یک ضلع مثلث برابر 5
$$
A=\frac{\sqrt{3}}{4} \times 5^{2}
$$
$$
A=\frac{\sqrt{3}}{4} \times 25
$$
$$
A=6.25 \times \sqrt{3}
$$
$$
A \approx 10.8
$$
مساحت قاعده هرم تقریبا برابر 10/8 است. وجههای جانبی از نوع مثلث متساوی الساقین هستند. مساحت مثلث متساوی الساقین توسط فرمول زیر محاسبه میشود:
$$
A = \frac {h \times b } { 2 }
$$
- A: مساحت مثلث
- h: ارتفاع مثلث برابر 10
- b: قاعده مثلث برابر 5
$$
A = \frac {10 \times 5 } { 2 }
$$
$$
A = \frac {50 } { 2 }
$$
$$
A = 25
$$
مساحت یکی از مثلثهای متساوی الساقین (یکی از وجههای جانبی) برابر 25 است. بنابراین، مساحت تمام وجههای جانبی برابر است با:
$$
25 \times 3 = 75
$$
با جمع مساحت قاعده و مساحت تمام وجههای جانبی، مساحت گسترده هرم به دست میآید:
$$
10.8 + 75 = 85.8
$$
در نتیجه، مساحت گسترده هرم برابر 85/8 است. مساحت گسترده هرم، مساحت هرم را نمایش میدهد.
مثال 7: تعیین اندازه ضلع های هرم مربعی با استفاده گسترده
هرم زیر، دارای قاعده مربعی شکل است. با توجه به اندازههای نمایش داده شده در تصویر، اندازه هر یک از ضلع های هرم را تعیین کنید. مساحت این هرم چگونه به دست میآید؟
برای تعیین اندازه ضلع های هرم، گسترده آن را رسم میکنیم. اندازه یکی از ضلعهای قاعده و یکی از ضلعهای وجه جانبی در تصویر بالا مشخص است. این اندازهها را در گسترده نیز یادداشت میکنیم.
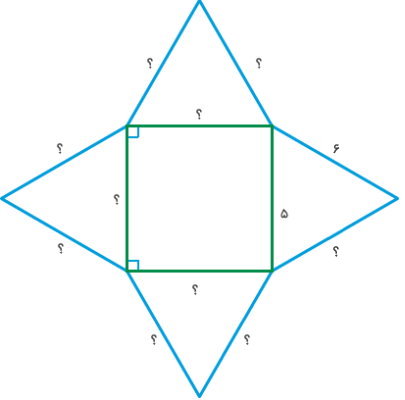
با توجه به صورت مسئله، قاعده هرم به شکل مربع است. بنابراین، اندازه تمام ضلعهای قاعده برابر با 5 خواهد بود.
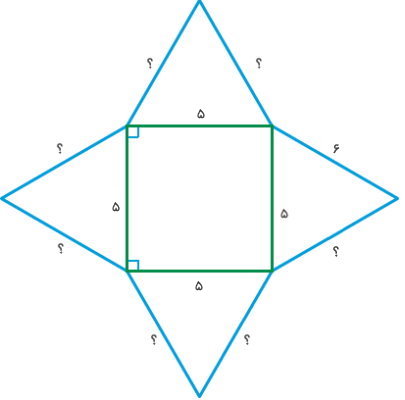
در هرم با قاعده مربع، ساقهای تمام مثلثها (وجههای جانبی)، مساوی هستند. در نتیجه، اندازه ضلعهای مجهول در تصویر بالا، برابر 6 خواهد بود.
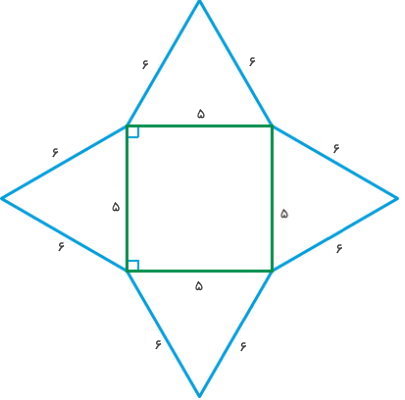
مساحت هرم، به صورت زیر محاسبه میشود:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم
با توجه به گسترده بالا، مساحت هرم نمایش داده شده در این مثال از رابطه زیر به دست میآید:
مساحت مثلثها + مساحت مربع = مساحت هرم
مساحت مربع، یک ضلع ضربدر خوش است. مساحت مثلث نیز برابر ارتفاع ضربدر قاعده تقسیم بر دو است. البته به دلیل مشخص بودن اندازه ساق، امکان تعیین ارتفاع مثلث به کمک قضیه فیثاغورس وجود دارد. در مثال بعدی، نحوه محاسبه ارتفاع وجههای جانبی (طول مایل) را توضیح خواهیم داد.
مثال 4: محاسبه مساحت هرم با قاعده مستطیل
مساحت هرم مستطیلی زیر را محاسبه کنید. (ارتفاع هرم بر روی مرکز مستطیل قرار دارد.)
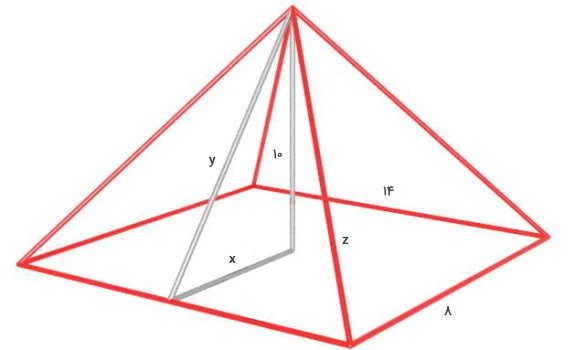
در تصویر بالا، ارتفاع هرم، طول قاعده و عرض قاعده داده شدهاند. طبق رابطه کلی مساحت هرم، داریم:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم
به دلیل داشتن طول و عرض مستطیل، مساحت قاعده با استفاده از فرمول مساحت مستطیل تعیین میشود:
عرض × طول = مساحت مستطیل
8 × 14 = مساحت مستطیل
112 = مساحت مستطیل
در مرحله بعد، به سراغ محاسبه مساحت وجههای جانبی هرم میرویم. این کار با استفاده از تعیین طول مایل (y) هر یک از وجههای جانبی انجام میشود. ارتفاع هرم بر روی مرکز مستطیل فرود آمده است. از اینرو، فاصله آن تا طول مستطیل، برابر نصف عرض و فاصله آن تا عرض مستطیل، برابر نصف طول خواهد بود. به عبارت دیگر:
4 = x
مطابق با تصویر، طول مایل هر وجه جانبی، وتر مثلث قائم الزاویهای به ساق 10 و x است. با نوشتن قضیه فیثاغورس، طول مایل (y) به دست میآید:
$$
y^2 = x^2 + 10^2
$$
$$
y^2 = 4^2 + 10^2
$$
$$
y^2 = 16 + 100
$$
$$
y^2 = 116
$$
$$
y = \sqrt {116}
$$
$$
y \approx 10.77
$$
طول مایل وجههای جانبی برابر 10/77 است. اکنون، مساحت هر وجه را توسط فرمول مساحت مثلث (ارتفاع ضربدر قاعده تقسیم بر دو) محاسبه میکنیم:
2 ÷ (10.77 × 10) = مساحت مثلث
53.85 = مساحت مثلث
مساحت یکی از وجههای جانبی برابر 53/85 است. مساحت چهار وجه برابر خواهد بود با:
53.85 × 4 = مساحت وجههای جانبی
215.4 = مساحت وجههای جانبی
مساحت وجههای جانبی هرم برابر 215/4 است. به این ترتیب، مساحت هرم برابر است با:
215.4 + 112 = مساحت هرم
327.4 = مساحت هرم
مساحت هرم برابر 327/4 است.
سوالات متداول در رابطه با مساحت هرم
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت هرم پاسخ میدهیم.
تعریف مساحت هرم چیست ؟
مساحت هرم، اندازه سطح پوشش دهنده قاعده و وجههای جانبی آن است.
مساحت هرم چگونه بدست می آید ؟
مساحت هرم با استفاده از فرمول کلی محاسبه برابر TSA = BSA + LSA به دست میآید. در این فرمول، BSA، مساحت قاعده و LSA، مجموع مساحت وجههای جانبی را نمایش میدهد.
گسترده هرم چیست ؟
گسترده، نمایش دو بعدی حجم سه بعدی هرم است. با تا کردن مناسب گسترده هرم میتوان شکل سه بعدی آن را ایجاد کرد.
مساحت گسترده هرم چیست ؟
مساحت گسترده هرم، همان مساحت کل هرم است.











خیلی خوب عالی توضیح دادید
واقعا ممنونم