شبیه سازی مدار در پایتون — به زبان ساده

در این آموزش، چگونگی شبیه سازی سیستم‌های دینامیکی در حوزه زمان را در قالب یک مثال بیان می‌کنیم که در تحلیل و کنترل سیستم‌ها کاربرد دارد. همچنین، با شبیه سازی مدار در پایتون آشنا می‌شویم.

یک مدار RL ساده در شکل ۱ نشان داده شده است. می‌خواهیم جریان $$i(t)$$ را به دست آوریم. فرض می‌کنیم منبع ولتاژ $$ v_s = V _ { DC } $$ معلوم باشد (برای مثال، ۵ ولت). در ابتدا، مدار باز است. فرض می‌کنیم کلید در $$t _ 0$$ روشن شود. معادله دیفرانسیل معمولی (ODE) را برای توصیف مدل مدار به صورت زیر می‌نویسیم:

 $$ \large V _ { DC } = R i ( t ) + L \frac { d i ( t)} { d t} \;\;\;\;\; ( 1 ) $$

در سیستم ساده (۱)، می‌توانیم فرم بسته‌ای برای $$i(t)$$ با استفاده از روش‌های حل معادلات دیفرانسیل به دست آوریم.

فیلم آموزش برنامه نویسی پایتون Python – تکمیلی – بخش یکم در فرادرس

کلیک کنید

جواب $$i(t)$$ از معادله (۱) دارای دو مؤلفه $$ i _ 1 ( t) $$ و $$ i _ 2 ( t) $$ است:

$$ \large i ( t ) = i _ 1 ( t ) + i _ 2 ( t ) \;\;\;\;\; (2) $$

که در آن، $$ i _ 1 ( t ) $$ مؤلفه اجباری یا پاسخ حالت ماندگار است که یک جواب خصوصی است و در معادله (۱) صدق می‌کند، و $$ i _ 2 ( t) $$ مؤلفه گذرایی است که در معادله همگن زیر صادق است:

$$ \large 0 = R i _ 2 ( t ) + L \frac { d i _ 2 ( t)}{ d t } . \;\;\;\;\; (3)$$

برای $$ i _ 1 ( t ) $$ می‌توانیم یک جواب را حدس بزنیم. برای مثال، با مقایسه سمت چپ ($$ V _ { DC }$$) با سمت راست ($$ R i + \frac { d i } { d t } $$) معادله (۱)، حدس می‌زنیم که $$ i _ 1 ( t) $$ یک عدد ثابت با مشتق صفر باشد. بنابراین، سمت راست $$ R i _ 1 $$ خواهد شد. در نتیجه، داریم:

$$ \large i _ 1 = \frac { v _ { DC}} { R } . \;\;\;\; (4) $$

برای $$ i _ 2 $$، فرم عمومی همگن مرتبه اول به صورت $$ K e ^ { s ( t - t _ 0 )} $$ است که در آن، $$ K$$ و $$s$$ اعداد ثابتی هستند. با برابر قرار دادن $$ i _ 2 ( t ) $$ با $$ K e ^ { s ( t - t _ 0 ) } $$ در (۳)، داریم:

$$ \large 0 = K ( R + L s )  e ^ {s ( t - t _ 0 ) }  \;\;\;\;\; (5)$$

برای آنکه سمت راست برابر با صفر باشد، باید داشته باشیم:

$$ \large s = - \frac { R } {L}. $$

با استفاده از شرایط اولیه می‌توانیم $$K$$ را به دست آوریم. ابتدا، عبارت توصیف کننده $$ i ( t) $$ را پیدا می‌کنیم:

$$ \large i ( t) = \frac { V _ { DC } } { R } + K e ^ {-\frac { R } { L } ( t - t _ 0 ) } . \;\;\;\;\; ( 6 ) $$

در $$ t = t _ 0 ^ + $$ ($$^ + $$ لحظه دقیقاً بعد از وصل شدن کلید را نشان می‌دهد)، می‌دانیم که جریان در مقدار ۰ نگه داشته می‌شود، زیرا مدار دارای یک سلف است و جریان گذرنده از یک سلف نمی‌تواند ناگهانی تغییر کند. بنابراین:

$$ \large 0 = \frac { v _ { DC} } { R} + K \implies K = - \frac { V _ { DC }} { R} . \;\;\;\;\; ( 7 ) $$

توصیف نهایی $$ i ( t) $$ به صورت زیر خواهد بود:

$$ \large i ( t) = \frac { V _ { DC} } { R} \left ( 1 - e ^ {- ( t - t _ 0 ) / \tau } \right ) , \; \; t \geq t _ 0 ^ + \;\;\;\;\; ( 8 ) $$

که در آن، $$ \tau = \frac { L } { R} $$.

پارامتر $$ \tau$$ به عنوان ثابت زمانی شناخته می‌شود. وقتی $$ t = t _ 0 + \tau$$، داریم:

$$ \large i ( t _ 0 + \tau ) = ( 1 - e ^ { - 1 } ) i ( \infty ) = 0.63 \times i ( \infty ) $$

که در آن، $$ i ( \infty)$$ مقدار حالت مانای جریان است و $$ i ( \infty) = \frac { v _ { DC}} { R} $$. یک ثابت زمانی مشخص می‌کند که پاسخ سیستم چقدر سریع است. ثابت زمانی یکی پارامتر مهم در دینامیک سیستم است. یک پارامتر دیگر، پهنای باند است. پهنای باند بزرگ، یک پاسخ سریع را نشان می‌دهد.

با استفاده از تبدیل لاپلاس نیز می‌توانیم عبارت بسته‌ای به دست آوریم. در حوزه لاپلاس، معادله (۱) به صورت زیر بیان می‌شود:

$$ \large \frac { V _ { DC} } { s } = R I ( s ) + L ( s I ( s ) - i ( t _ 0 ^ + )) \;\;\;\;\; (9 ) $$

که در آن، $$ I ( s ) = \mathcal {L}( i ( t)) $$ توصیف حوزه لاپلاس جریان است.

در $$ t _ 0 ^ + $$، جریان ۰ است. این به آن دلیل است که در شرایط اولیه مدار باز بوده و جریانی وجود نداشته است. علاوه بر این، باید دقت کرد که یک سلف در مسیر جریان داریم. جریان گذرنده از یک سلف نمی‌تواند در هنگام وصل شدن کلید جهش ناگهانی داشته باشد. بنابراین، $$ i ( t _ 0 ^ + ) = 0 $$.

براساس (۹)، عبارت جریان به صورت زیر است:

$$ \large \begin {align*}
I ( s ) & = \frac { v _ { DC}} { s ( R + L s ) } \\
& = \frac { v _ { D C } }{ R} \left ( \frac { 1 } { s } - \frac { 1 } { s + R / L } \right )
\end {align*} \;\;\;\;\; (10) $$

با استفاده از تبدیل لاپلاس معکوس، می‌توانیم عبارت حوزه زمان را به دست آوریم:

$$ \large \begin {align*} i ( t ) = \frac { V _ { D C } }{ R} \left ( 1 - e ^ {-(t-t_0) / \tau } \right ) \end {align*} , \;\; t \geq t _ 0 ^ + \;\;\;\;\; (11) $$

که در آن، $$ \tau = L / R $$.

همان‌طور که دیدیم، عبارت $$ i ( t ) $$ که براساس دو روش حل معادله و تبدیل لاپلاس به دست آمد مشابه بود.

در مدل یک سیستم پیچیده، به دست آوردن عبارات حوزه زمان برای متغیرهای دلخواه کار آسانی نیست. در عوض، می‌توان از انتگرال‌گیری عددی برای یافتن مقادیر متغیرهای ODE در طول زمان استفاده کرد.

در ادامه، روش‌های انتگرال‌گیری عددی را معرفی می‌کنیم.

روش‌های انتگرال‌گیری عددی برای شبیه سازی مدار در پایتون

روش‌های انتگرال‌گیری عددی متنوعی در کتاب‌های مرجع وجود دارد که در اینجا سه روش معروف اویلر پیشرو، رانگ کوتا و ذوزنقه‌ای را بیان می‌کنیم.

فیلم آموزش برنامه نویسی پایتون + مثال های عملی در Python در فرادرس

کلیک کنید

روش اویلر پیشرو

معادلات دیفرانسیل زیر را در نظر بگیرید:

$$ \large \frac { d x } { d t } = f ( x ) \;\;\;\;\; ( 12) $$

که در آن، $$ x \in \mathbb { R} ^ n $$ و $$ f$$ یک نگاشت $$ f : \mathbb { R} ^ n \implies \mathbb { R} ^ n $$ است. هدف انتگرال‌گیری عددی یافتن $$ x ( t _ 1 ) $$، $$ x ( t_ 2 )$$، ... و $$ x ( T)$$ در بازه زمانی $$ t _ 0 \sim T $$ برای شرایط اولیه $$ x ( t _ 0 ) $$ است.

اگر گام ثابت $$h$$ را انتخاب کنیم، داریم:

$$ \large \begin {aligned} t _ { 1 } & = t _ { 0 } + h \\ \vdots & = \vdots \\ t _ { k } & = t _ { k - 1 } + h = t _ { 0 } + k h \\ \vdots & = \vdots \\ t _ { N } & = t _ { N - 1 } + h = t _{ 0 } + N h \end {aligned} $$

می‌خواهیم $$x _ k $$ را برای $$ k = 1, \cdots , N$$ به دست آوریم، که در آن، $$N= ( T - t_ 0 ) / h $$، و $$ x _ k $$ مقدار تقریب زده شده $$ x ( t _ k ) $$ است.

براساس سری تیلور، $$ x ( t _ { k+1})$$ را می‌توان برحسب $$ x ( t_ k ) $$ و مشتقات $$x$$ در $$ t _ k $$ توصیف کرد.

$$ \large \begin {aligned} x \left ( t _ { k + 1 } \right ) & = x \left ( t _ { k } \right ) + \dot { x } \left ( t _ { k } \right ) h + O \left ( h ^ { 2 } \right ) \\ & \approx x \left ( t _ { k } \right ) + \dot { x } \left ( t _ { k } \right ) h \\ & = x \left ( t _ { k } \right ) + f \left ( x \left ( t _ { k } \right ) \right ) h \end {aligned} $$

که در آن، $$ O ( \cdot)$$ جملات مرتبه بالاتر را نشان می‌دهد.

اگر به جای $$ x ( t _ k ) $$ مقدار تقریب زده شده $$ x _ k $$ را قرار دهیم، داریم:

$$ \large x _ { k + 1 } = x _ k + f ( x _ k ) h . \;\;\;\;\; ( 13 ) $$

رابطه (۱۳) روش اویلر پیشرو است. اگر فرض کنیم که خطای بین $$ x ( t _ k ) $$ و $$ x_ k $$ قابل چشم‌پوشی است، خواهیم داشت:

$$ \large x ( t _ { k + 1 } ) - x _ { k + 1 } = O ( h ^ 2 ) \;\;\;\;\; (14 ) $$

بنابراین، دقت روش اویلر $$ O ( h ^ 2 ) $$ است.

برنامه شبیه سازی مدار در پایتون را به صورت زیر می‌نویسیم:

1import math,pylab
2# define the dynamic equation to compute di/dt # R*i + L. di/dt = v
3def fun_didt(R, L, v, i):
4di_dt = (v-R*i)/L;
5return di_dt
6# Use trapezoidal method to conduct numerical integration
7# step 1, initial condition
8# voltage is a dc voltage. for all time being, voltage is 5V.
9step_size = 0.01
10n_steps = 1000
11v = 5.0
12R = 0.1
13L = 0.1
14i_data =[]
15v_data =[]
16i = 0
17for k in range(n_steps):
18v_data.append(5.0)
19i_data.append(i)
20# compute current
21i = i + fun_didt(R, L, v, i)*step_size;
22tt = [k*step_size for k in range(n_steps)]
23pylab.plot(tt, i_data)
24pylab.xlabel('time (sec)');
25pylab.show()

در برنامه بالا، ابتدا تابع fun_didt تعریف شده است. این تابع مشتق جریان را برای مقادیر معلوم ولتاژ منبع، جریان آن و پارامترهای $$R$$ و $$L$$ محاسبه می‌کند. گام شبیه‌سازی $$h$$ برابر با $$0.01$$ ثانیه و تعداد کل گام‌ها ۱۰۰۰ است. اندازه ولتاژ‌ DC برابر با ۵ ولت، مقاومت ۰٫۱ اهم، و اندوکتانس ۰٫۱ هانری است. دو فهرست i_data و v_data برای ذخیره جریان و ولتاژ محاسبه شده در هر گام مورد استفاده قرار می‌گیرد. جریان اولیه نیز برابر با صفر قرار داده شده است.

تکرار برای ۱۰۰۰ گام انجام می‌شود و در هر گام، جریان و ولتاژ‌ محاسبه شده در دو فهرست قرار داده می‌شوند. در هر گام، fun_didt فراخوانی شده و با روش اویلر پیشرو جریان گام بعدی محاسبه می‌گردد.

در نهایت، از pylab برای رسم شکل‌ها استفاده می‌شود. نتایج حاصل از شبیه‌سازی دینامیکی با برنامه پایتون بالا در شکل ۲ نشان داده شده است.

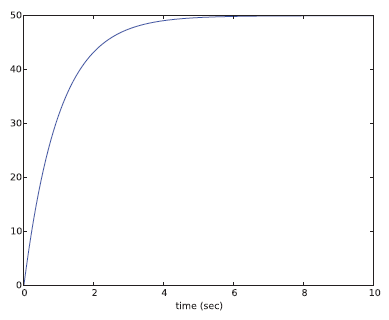
در متلب، با استفاده از دستور ode1 می‌توان انتگرال‌گیری را با استفاده از روش اویلر انجام داد.

روش رانگ کوتا

روشر اویلر، به دلیل دقت پایینی که دراد، چندان محبوب نیست. در روش رانگ کوتا، جمله مرتبه دوم نیز در نظر گرفته می‌شود. دقت روش رانگ کوتای مرتبه چهارم $$ O ( h ^ 5 ) $$ است. در حل‌کننده ODE متلب، رانگ کوتای مرتبه چهارم با ode4 نشان داده می‌شود.

$$ \large \begin {align*}
x _ { k + 1 } & = \frac { 1 } { 6 } ( k _ 1 + 2 k _ 2 + 2 k_ 3 + k _ 4 ) \\
k _ 1 & = f ( x _ k ) \\
k _ 2 & = f ( x _ k + \frac { h } { 2 } k _ 1 ) \\
k _ 3 &= f ( x _ k + \frac { h } { 2 } k _ 2 ) \\
k _ 4 & = f ( x _ k + h k _ 3 )
\end {align*} $$

روش ذوزنقه‌ای

دقت روش ذوزنقه‌ای $$ O ( h ^ 3 ) $$ است. در روش اویلر پیشرو، مشتق $$ x $$ در بازه $$ [ t _ k , t _ { k + 1 } ] $$ برابر با $$ f ( x ( t _ k )) $$ فرض می‌شود. در روش ذوزنقه‌ای، مشتق $$ f ( x ) $$ با خط متصل کننده دو نقطه $$ f ( x ( t _ k ))$$ و $$ f ( x ( t_ { k + 1 } ))$$، مطابق شکل ۳، تقریب زده می‌شود. بنابراین، از مساحت ذوزنقه برای جایگزینی با انتگرال‌گیری $$ f ( x ) $$ از $$t _ k $$ تا $$ t _ { k + 1 } $$ استفاده می‌کنیم.

$$ \large \begin {align*}
x _ { k + 1 } & = x _ k + \int _ { t _ k } ^ { t _ { k + 1 } } f ( x ) d t \\
& \approx x _ k + \frac { h } { 2 } ( f ( x _ k ) + f ( x _ { k + 1 } ) )
\end {align*} \;\;\;\;\; ( 16 ) $$

لازم به ذکر است که در روش ذوزنقه‌ای باید مشتق حالت در $$ t _ { k + 1 } $$ محاسبه شود. ابتدا روش اویلر پیشرو برای به دست آوردن تخمین $$ x _ { k + 1 } $$ اعمال می‌شود که آن را با $$ \tilde { x } _ { k + 1 } $$، مطابق رابطه اول (۱۷)، نمایش می‌دهیم. پس از آن، مطابق رابطه دوم (۱۷)، از روش ذوزنقه‌ای برای یافتن حالت در گام $$k + 1 $$ استفاده می‌کنیم.

$$ \large \begin {align*}
\tilde {x } _ { k + 1 } & = x _ k + h f ( x _ k ) \\
x _ { k + 1 } & = x _ k + \frac { h } { 2 } ( f ( x _ k )) + f ( \tilde { x } _ { k + 1 } ))
\end {align*} \;\;\;\;\; ( 1 7 ) $$

جدول ۱ مقایسه سه روش را برای نتایج انتگرل‌گیری عددی مدار RL نشان می‌دهد. مقادیر عددی، $$ x _ k - x ( t _ k ) $$  را نشان می‌دهند، که در آن، $$ x ( t _ k ) $$ با استفاده از فرم بسته تحلیلی (۸) محاسبه شده است. همان‌طور که می‌بینیم، روش رانگ کوتای مرتبه چهارم (RK4) دقیق‌ترین نتیجه را دارد، در حالی که دقت روش ذوزنقه‌ای بسیار بیشتر از روش اویلر پیشرو است.

جدول ۱: مقایسه خطاهای سه روش 

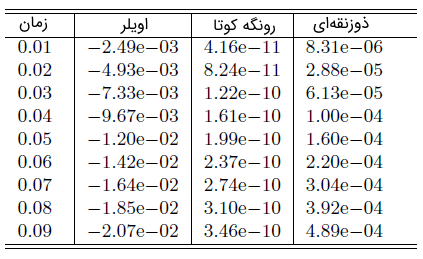
نتایج جدول بالا، از اجرای برنامه شبیه سازی مدار در پایتون به دست آمده است.

1import math,pylab
2# define the dynamic equation to compute di/dt
3# R*i + L. di/dt = v
4def fun_didt(R, L, v, i):
5di_dt = (v-R*i)/L;
6return di_dt
7step_size = 0.01; n_steps = 10;
8v = 5.0; R = 0.1; L = 0.1;
9i_data =[]; i_Eu = [];i_RK = []; i_Tr = []; v_data =[];
10i1 = 0; i2 = 0; i3 = 0;
11for k in range(n_steps):
12v_data.append(5.0)
13i_data.append(5.0/R*(1-math.exp(-R*step_size*k/L)))
14i_Eu.append(i1)
15i_RK.append(i2)
16i_Tr.append(i3)
17# Euler
18i1 = i1 + fun_didt(R, L, v, i1)*step_size;
19# Trapzoidal
20i3 = i3 + 0.5*(fun_didt(R, L, v, i1)+ fun_didt(R, L, v, i3))*step_size;
21# RK4
22k1 = fun_didt(R, L, v, i2)
23k2 = fun_didt(R, L, v, i2 + 0.5*step_size*k1)
24k3 = fun_didt(R, L, v, i2 + 0.5*step_size*k2)
25k4 = fun_didt(R, L, v, i2 + step_size*k3)
26i2 = i2 + step_size/6*(k1+2*k2+2*k3+k4)
27# print a table
28for k in range(n_steps):
29print step_size*k,i_data[k]-i_Eu[k],i_data[k]-i_RK[k],i_data[k]-i_Tr[k]

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش شبیه سازی با سیمیولینک Simulink
• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• آموزش برنامه نویسی پایتون – مقدماتی
• کاربرد تبدیل لاپلاس در تحلیل مدار — به زبان ساده
• رسم نمودار دو بعدی در متلب – از صفر تا صد
• دوقطبی در مدارهای الکتریکی — به زبان ساده

^^