کاربرد تبدیل لاپلاس در تحلیل مدار — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزشهای قبلی مجله فرادرس، درباره تبدیل لاپلاس و خواص آن بحث کردیم. تبدیل لاپلاس، یک ابزار ریاضی قدرتمند برای تجزیه و تحلیل و طراحی است. توانایی بررسی مدارها و سیستمها در حوزه s، ما را در فهم بهتر عملکرد واقعی سیستم کمک میکند. علاوه بر این، میتوانیم سیستمهای فیزیکی را سادهتر و سریعتر بررسی کنیم. در این آموزش، نحوه مدلسازی مدار در فضای s یا فرکانس و کاربرد تبدیل لاپلاس در مدار را معرفی میکنیم.
استفاده از تبدیل لاپلاس در مدارهای الکتریکی، سه گام دارد:
- تبدیل مدار از حوزه زمان به حوزه s
- حل مدار با استفاده از تحلیل گره، تحلیل مش، تبدیل منبع، جمع آثار، یا هر تکنیک دیگر
- اعمال تبدیل لاپلاس معکوس به پاسخ و به دست آوردن پاسخ در حوزه زمان
همانطور که میبینیم، فقط گام اول جدید است و درباره آن بحث میکنیم. از تحلیل فازور میدانیم که با استفاده از تبدیل لاپلاس میتوان هریک از اجزای یک مدار را در حوزه زمان، به حوزه فرکانس یا حوزه s بُرد.
رابطه ولتاژ-جریان یک مقاومت در حوزه زمان بهصورت زیر است:
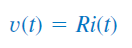
تبدیل لاپلاس این معادله برابر است با:
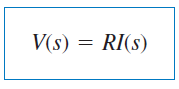
برای یک سلف داریم:
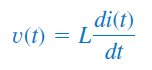
با اعمال تبدیل لاپلاس به دو طرف رابطه سلف، خواهیم داشت:
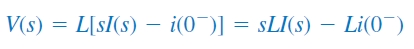
یا
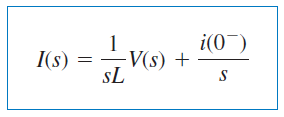
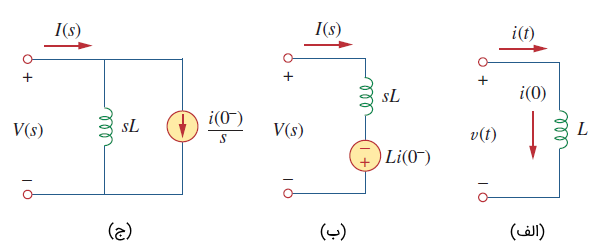
معادلهای حوزه s در شکل ۱ نشان داده شده که در آن، شرایط اولیه با منبع ولتاژ یا منبع جریان مدل شده است.
برای یک خازن داریم:
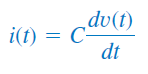
که تبدیل لاپلاس آن در فضای s بهصورت زیر است:
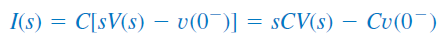
یا
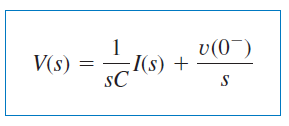
معادلهای حوزه s در شکل ۲ نشان داده شدهاند.
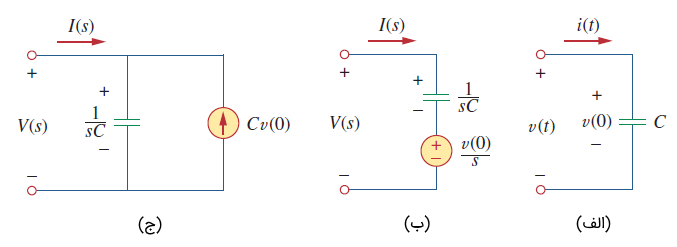
با استفاده از معادلهای حوزه s میتوان تبدیل لاپلاس را بهراحتی برای حل معادلات مرتبه اول و مرتبه دوم بهکار برد. همانطور که از معادلات (۳) تا (۸) مشخص است، شرایط اولیه، بخشی از تبدیل هستند. این، یکی از مزایای استفاده از تبدیل لاپلاس در تحلیل مدار است. یکی دیگر از مزایای تبدیل لاپلاس این است که میتوان پاسخ کامل (گذرا و حالت) ماندگار شبکه را با استفاده از آن بهدست آورد.
با فرض شرایط اولیه صفر برای سلف و خازن، روابط بالا را میتوان به معادلات زیر کاهش داد:
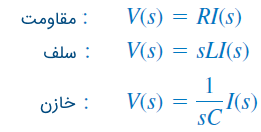
معادلهای حوزه s، در شکل ۳ نشان داده شدهاند.
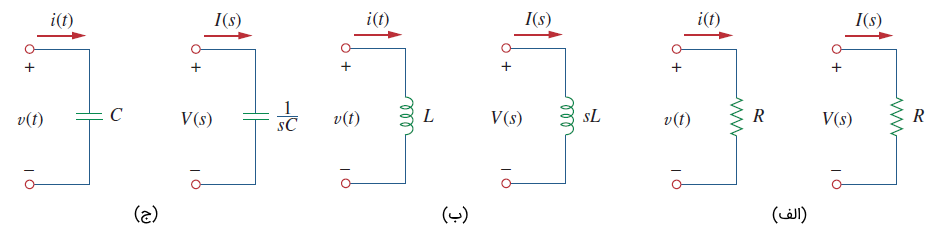
امپدانس در حوزه s، بهعنوان نسبت تبدیل لاپلاس ولتاژ به تبدیل لاپلاس جریان در شرایط اولیه صفر تعریف میشود:
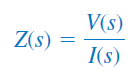
بنابراین، امپدانسهای سه عنصر مدار در حوزه s بهصورت زیر هستند:

جدول ۱ این روابط را بهطور خلاصه نشان میدهد. 
ادمیتانس در حوزه s برابر با معکوس امپدانس است:
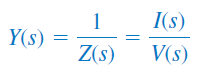
استفاده از تبدیل لاپلاس برای تحلیل مدار، این قابلیت را به ما میدهد که بتوانیم از منابع سیگنال مختلف، مانند ضربه، پله، شیب، نمایی و سینوسی استفاده کنیم.
مدل منابع وابسته و تقویتکنندههای عملیاتی را میتوان بهسادگی و با استفاده از این حقیقت که اگر تبدیل لاپلاس ، باشد، آنگاه تبدیل لاپلاس ، است (خاصیت خطی بودن)، بهدست آورد. مدل منبع وابسته، اندکی سادهتر است، چون فقط میتواند دو مقدار کنترلی داشته باشد: یک مقدار ثابت و ولتاژ یا جریان. بنابراین، داریم:
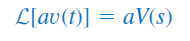
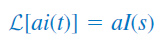
آپامپ ایدهآل را میتوان مانند یک مقاومت در نظر گرفت.
مثال برای کاربرد تبدیل لاپلاس در مدار
مقدار مدار شکل ۴ را با فرض شرایط اولیه صفر بهدست آورید.
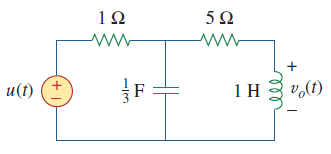
حل: ابتدا مدار را از حوزه زمان به حوزه s تبدیل میکنیم:
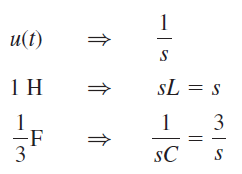
شکل ۵، مدار معادل را در حوزه s نشان میدهد.
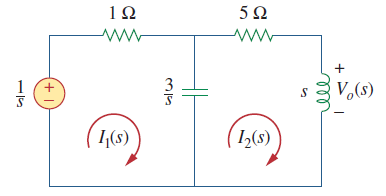
برای تحلیل مدار، از روش مش استفاده میکنیم. برای مش ۱ میتوان نوشت:
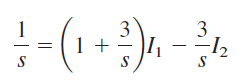
برای مش ۲ نیز داریم:
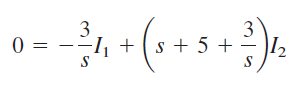
یا
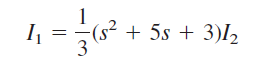
با جایگذاری معادله (۱۶) در معادله (۱۵)، به معادله زیر میرسیم:
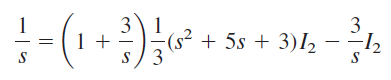 " width="391" height="80">
" width="391" height="80">
با ضرب معادله اخیر در ، داریم:
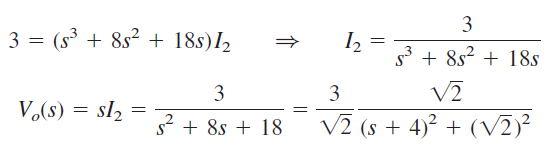
اگر از ولتاژ تبدیل لاپلاس معکوس بگیریم، رابطه آن در حوزه زمان بهدست میآید:
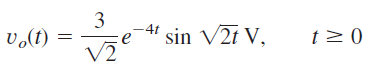
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^













خیلی ممنون
سلام…ببخشید من یه سوال دارم…در تبدیل لاپلاس ما برای یک عدد انرا در یک بر s تقسیم میکنیم …ولی چرا ما این کار رو واسه مقاومت این کار رو نمیکنیم؟؟؟چون مقاومت هم یک عدد حقیقی هست پس بایستی بر s تقسیم شه
سلام.
آن تابعی که تبدیل لاپلاسش برابر با s1 است، تابع پله یا همان u(t) است، نه عدد ثابت.
موفق باشید.
بی نظیر هستین اقای زندی خدا خیرتون بده