مدار مرتبه اول RL — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

همانطور که در آموزشهای پیشین مجله فرادرس گفتیم، مدارهای مرتبه اول مدارهایی هستند که از ترکیب دوتایی عناصر پسیو ساخته میشوند. این مدارها، مدار شامل مقاومت و خازن (مدار RC) و مدار متشکل از مقاومت و سلف (مدار RL) هستند. قبلاً، درباره مدارهای RC بهتفصیل بحث کردیم. در این آموزش، مدار مرتبه اول RL را بررسی خواهیم کرد و پاسخ آن را در حالت بدون ورودی و با ورودی پله بهدست خواهیم آورد.
مدار مرتبه اول RL بدون منبع
یک مدار RL را بدون منبع میگوییم اگر منبع dc آن بهطور ناگهانی قطع شود. با قطع منبع، انرژی ذخیرهشده قبلی در مدار تخلیه میشود.
ترکیب سری یک مقاومت و یک سلف را در نظر بگیرید که سلف از قبل دارای انرژی شده است (شکل 1). هدف، تعیین پاسخ مدار است که به دلایل آموزشی، فرض میکنیم جریان سلف باشد.
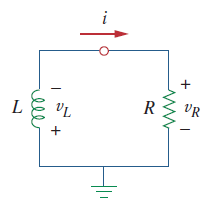
میتوان فرض کرد در زمان سلف دارای جریان اولیه زیر است:
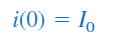
که انرژی متناظر با این جریان، برابر است با:
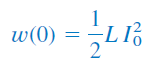
با اعمال KVL در حلقه مدار شکل ۱، داریم:
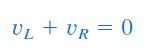
که در آن، و هستند. بنابراین:
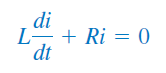
یا
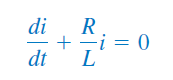
با کمی تغییرات جبری و انتگرالگیری، داریم:
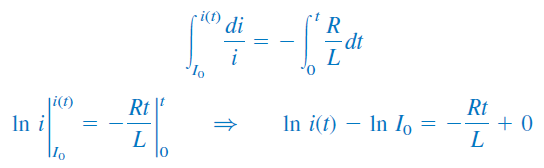
یا
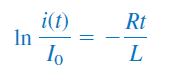
اگر دو طرف رابطه بالا را به توان برسانیم، خواهیم داشت:
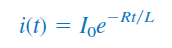
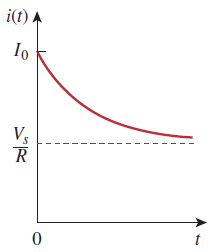
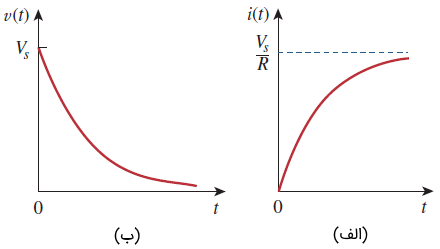
عبارت بالا نشان میدهد پاسخ جریان مدار RL، یک تابع نزولی نمایی از جریان اولیه است. از آنجایی که پاسخ به انرژی ذخیرهشده و مشخصات فیزیکی مدار وابسته است و به منابع ولتاژ یا جریان خارجی بستگی ندارد، آن را پاسخ طبیعی (Natural Response) مدار مینامند. به عبارت دیگر، پاسخ طبیعی یک مدار، رفتار (ولتاژ و جریان) آن مدار بدون هیچ منبع تحریک خارجی است.
پاسخ طبیعی مدار در شکل ۲ نشان داده شده است. توجه کنید که در ، همان شرایط اولیه رابطه (۱) را داریم. با افزایش ، جریان به صفر کاهش پیدا میکند. سرعت کاهش جریان را با ثابت زمانی (Time Constant) یا نشان میدهند. به عبارت بهتر، ثابت زمانی یک مدار، زمان مورد نیاز برای آن است که پاسخ به یا 36.8 درصد مقدار اولیهاش کاهش پیدا کند.
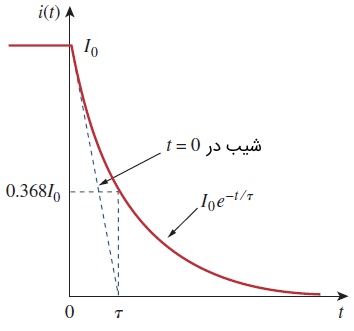
ثابت زمانی مدار RL بهصورت زیر است:
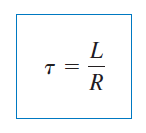
اکنون میتوانیم رابطه (۶) را برحسب ثابت زمانی بنویسیم:
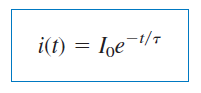
با استفاده از رابطه جریان اخیر، میتوان ولتاژ مقاومت را بهدست آورد:
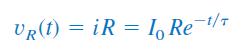
توان اتلافی مقاومت نیز بهصورت زیر محاسبه میشود:
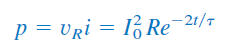
بنابراین، انرژی جذبشده مقاومت برابر است با:
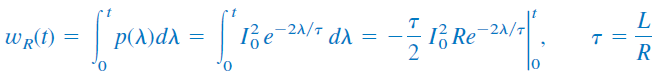
یا
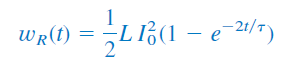
اگر ، آنگاه را داریم که برابر با همان مقدار انرژی ذخیرهشده اولیه در سلف () است.
بهعنوان نتیجهگیری، میتوان گفت دو پارامتر مهم برای مدار مرتبه اول RL بدون منبع وجود دارد که جریان اولیه سلف و ثابت زمانی هستند. با استفاده از این دو مورد میتوان پاسخ مدار را در قالب جریان سلف بهدست آورد. پس از آنکه جریان سلف بهدست آمد، سایر متغیرها (ولتاژ سلف ، ولتاژ مقاومت و جریان مقاومت ) را میتوان تعیین کرد.
در ثابت زمانی ، معمولاً مقاومت معادل تونن از دو سر سلف است. سلف نیز، سلف معادل مدار است.
توابع تکین
قبل از اینکه وارد بحث درباره نوع دیگر مدارهای مرتبه اول RL شویم، لازم است چند مفهوم ریاضی را بیان کنیم که موجب تسهیل درک تحلیل گذرا میشوند. آشنایی اولیه با توابع تکین (Singularity Functions) ما را در تحلیل پاسخ مدارهای مرتبه اول به اعمال ناگهانی منابع ولتاژ یا جریان dc کمک خواهد کرد.
توابع تکین که توابع سوئیچینگ یا کلیدزنی نیز نامیده میشوند، در تحلیل مدار بسیار مفید خواهند بود. این توابع، تقریبهای مناسبی برای سیگنالهای سوئیچینگ هستند که به مدار اعمال میشوند. توابع تکین، برای توصیف مناسب و فشرده برخی پدیدههای مدار، خصوصاً پاسخ مدارهای RC و RL مفید هستند. بنا بر تعریف، توابع تکین، توابعی ناپیوسته هستند یا مشتقهای ناپیوسته دارند. توابع تکین پرکاربرد که در تحلیل مدارهای الکتریکی مورد استفاده قرار میگیرند، پله واحد، ضربه واحد و شیب واحد هستند.
تابع پله واحد
تابع پله واحد برای مقادیر منفی ، صفر و برای مقادیر مثبت برابر با ۱ است.
به بیان ریاضی:
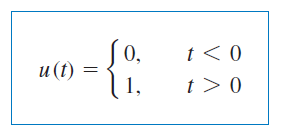
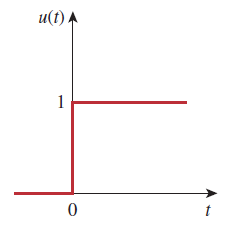
تابع پله واحد در که تغییر ناگهانی از 0 به 1 رخ میدهد، تعریف نشده است. این تابع، مانند سایر توابع ریاضیاتی مثل سینوس و کسینوس بدون بُعد است. شکل ۳، تابع پله واحد را نشان میدهد. اگر تغییر ناگهانی به جای در () رخ دهد، تابع پله بهشکل زیر خواهد بود:
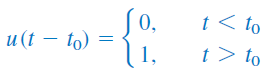
در این حالت میگوییم، بهاندازه ثانیه تاخیر یافته است (شکل 4 (الف)). برای بهدست آوردن رابطه (13) از رابطه (12)، میتوان بهسادگی را با جایگزین کرد. اگر تغییر ناگهانی در اتفاق افتد، تابع پله را میتوان بهصورت زیر نوشت:
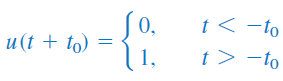
بدین ترتیب، مطابق شکل ۴ (ب)، بهاندازه ثانیه جلو میافتد.
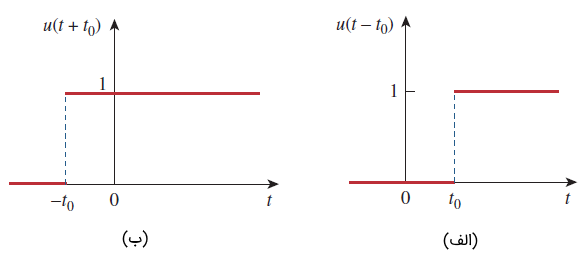
از تابع پله برای نشان دادن تغییر ناگهانی در ولتاژ یا جریان استفاده میکنیم. این کار مخصوصاً در سیستمهای کنترل و کامپیوترهای دیجیتال کاربرد دارد. برای مثال، ولتاژِ
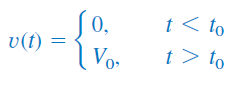
را میتوان با تابع پله واحد زیر نشان داد:
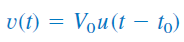
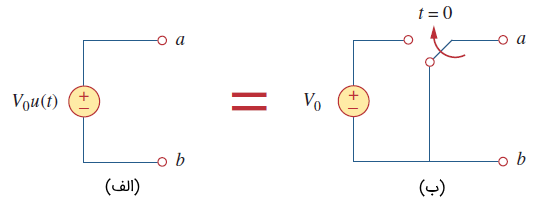
اگر را در نظر بگیریم، آنگاه را میتوان بهصورت تابع پله نوشت. منبع ولتاژ در شکل ۵ (الف) و مدار معادل آن، در شکل ۵ (ب) نشان داده شده است. از شکل ۵ (ب) مشخص است که ترمینالهای a-b در اتصال کوتاه هستند () و برای ، ولتاژ برابر است. به طریق مشابه، منبع جریان و مدار معادل آن، در شکل ۶ (الف) و ۶ (ب) نشان داده شدهاند. همانطور که میبینیم، برای ، منبع، مدار باز است () و در جریان آن برابر با خواهد بود.
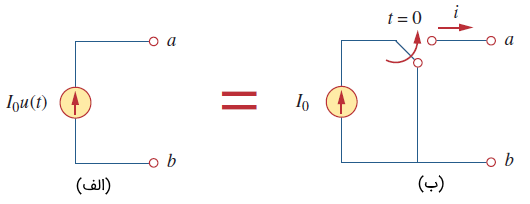
تابع ضربه واحد
مشتق تابع پله واحد ، تابع ضربه واحد است که بهصورت زیر نوشته میشود:

تابع ضربه واحد را، تابع دلتا نیز مینامند. شکل 7 این تابع را نشان میدهد. تابع ضربه واحد ، جز در تعریف نشده است.
جریانها و ولتاژهای ضربهای مدار، بر اثر کلیدزنی یا منابع ضربهای ایجاد میشوند. اگرچه تابع ضربه واحد از نظر فیزیکی قابل پیادهسازی نیست (مانند منابع ایدهآل، مقاومتهای ایدهآل و غیره)، اما ابزار ریاضی بسیار مفیدی است. تابع ضربه را میتوان بهعنوان یک شوک در نظر گرفت یا بهعنوان یک پالس بسیار کوتاه با مساحت واحد تصور کرد. به زبان ریاضی، میتوان نوشت:
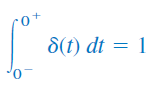
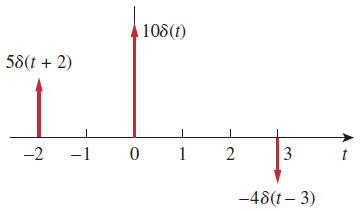
که در آن، ، زمان را اندکی قبل از و زمان را اندکی بعد از نشان میدهد. مساحت واحد را بهعنوان شدت تابع ضربه میشناسند. وقتی یک ضربه، شدت بیشتری نسبت به واحد داشته باشد، مساحت آن، برابر با آن شدت است. برای مثال، مساحت تابع ضربه ، برابر با 10 است. شکل ۸، توابع ضربه ، و را نشان میدهد.
برای آنکه تاثیر تابع ضربه را بر سایر توابع پیدا کنیم، انتگرال زیر را محاسبه میکنیم:
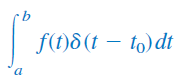
که در آن، . از آنجایی که مقدار جز در برابر با صفر است، انتگرالده جز در برابر با صفر است. بنابراین:
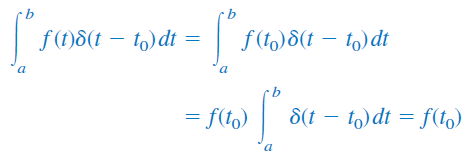
یا
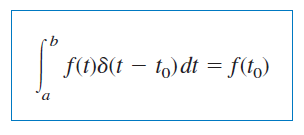
رابطه بالا نشان میدهد وقتی از حاصلضرب یک تابع و تابع ضربه، انتگرال بگیریم، مقدار تابع در نقطهای بهدست میآید که ضربه اعمال شده است. این ویژگی تابع ضربه که بسیار هم مفید است، خاصیت نمونهبرداری (Sampling) یا جابهجایی (Shifting) نامیده میشود. در حالت خاص، معادله (19) را میتوان برای بهصورت زیر نوشت:
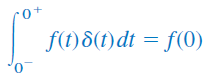
تابع شیب واحد
انتگرالگیری از تابع پله واحد ، تابع شیب واحد را نتیجه خواهد داد:
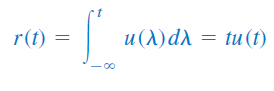
یا
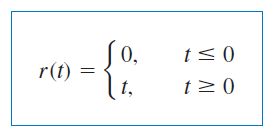
تابع شیب واحد، برای مقادیر منفی، برابر با صفر است و برای های مثبت، یک شیب واحد است. شکل 9، تابع شیب واحد را نشان میدهد. در حالت کلی، یک شیب، تابعی است که با نرخ ثابتی تغییر میکند.
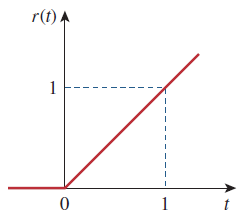
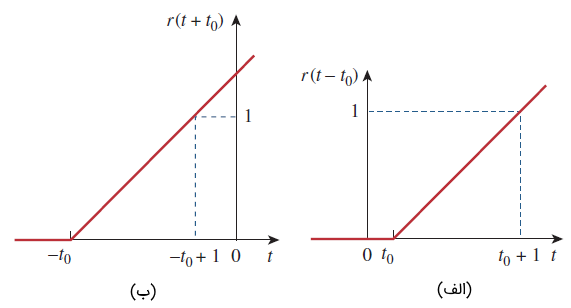
تابع شیب واحد، را میتوان مطابق شکل ۱۰، عقب یا جلو برد. برای یک تابع شیب واحد تأخیریافته، داریم:
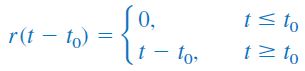
و یک تابع شیب پیشافتاده بهصورت زیر است:
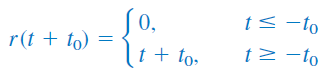
بهخاطر داشته باشید که سه تابع تکین (ضربه، پله و شیب) را میتوان با مشتق یا انتگرال به یکدیگر مربوط کرد:
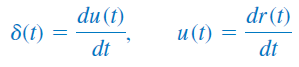
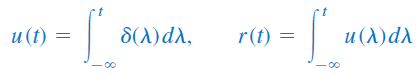
هرچند توابع تکین دیگری نیز وجود دارد، اما ما با این سه تابع سروکار داریم.
پاسخ پله یک مدار RL
وقتی یک منبع dc بهطور ناگهانی به مدار RL اعمال شود، منبع ولتاژ یا جریان را میتوان با یک تابع پله مدل کرد که پاسخ آن، بهعنوان پاسخ پله شناخته میشود.
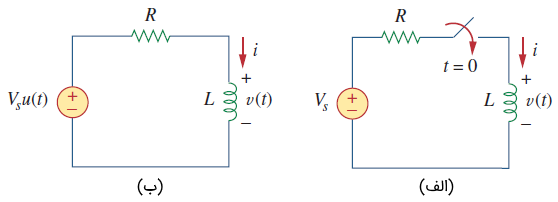
مدار RL شکل 1۱ (الف) را در نظر بگیرید که میتوان آن را با مدار شکل 1۱ (ب) جایگزین کرد. در این شکل، یک منبع ولتاژ dc ثابت است. در اینجا نیز جریان سلف را بهعنوان پاسخ مدار در نظر میگیریم.
پاسخ را میتوان بهعنوان مجموع پاسخ گذرا و حالت ماندگار نوشت:
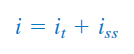
همانگونه که میدانیم، پاسخ گذرا همیشه یک نمایی کاهشی است:
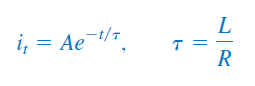
که در آن، یک ثابت است و باید آن را تعیین کرد.
پاسخ حالت ماندگار، مقداری از جریانی است که پس از یک مدت طولانی بعد از بسته شدن کلید در مدار برقرار است. پاسخ گذرا اساساً پس از ۵ ثابت زمانی از بین میرود. در آن زمان، سلف اتصالکوتاه میشود و ولتاژ دو سر آن صفر خواهد بود. در نتیجه، کل ولتاژ منبع در دو سر مقاومت ظاهر میشود. بنابراین، پاسخ حالت ماندگار برابر است با:
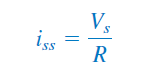
در نتیجه، با جمع روابط (29) و (30)، جریان سلف را میتوان بهصورت زیر نوشت:
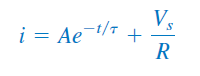
اکنون باید ثابت را از مقدار اولیه تعیین کنیم. فرض میکنیم، مقدار اولیه جریان سلف است. از آنجایی که جریان سلف بهطور ناگهانی تغییر نمیکند، داریم:
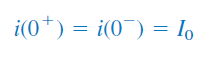
بنابراین، در رابطه (۳۱) بهصورت زیر درمیآید:
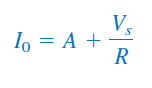
از رابطه بالا، مقدار را بهدست میآوریم:
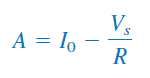
با جایگذاری در معادله (۳۱) داریم:
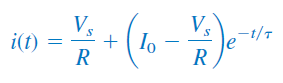
پاسخ بالا، پاسخ کامل مدار RL است که نمودار آن در شکل ۱۲ نشان داده شده است.
پاسخ معادله (۳۳) را میتوان بهصورت زیر نوشت:
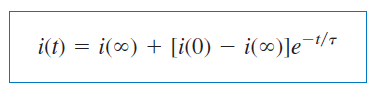
که در آن، ، جریان اولیه در و ، مقدار نهایی یا حالت ماندگار است. بنابراین، برای یافتن پاسخ پله یک مدار RL، به سه پارامتر نیاز داریم:
- جریان اولیه سلف
- جریان نهایی سلف
- ثابت زمانی .
مورد ۱ را میتوان در زمان برای مدار بهدست آورد. موارد 2 و ۳ نیز در بهدست میآیند. با محاسبه این موارد، میتوان پاسخ را از رابطه (۳۴) بهدست آورد.
توجه کنید اگر کلید بهجای در لحظه سوئیچ شود، یک تاخیر زمانی در رابطه (34) ایجاد خواهد شد:
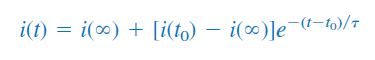
که در آن، ، مقدار اولیه در است. روابط (34) و (35) فقط درمورد پاسخ پله کاربرد دارند، یعنی وقتی تحریکِ ورودی، ثابت است.
اگر فرض کنیم سلف در حالت اولیه انرژی نداشته باشد، مقدار را در معادله (34) قرار میدهیم و خواهیم داشت:
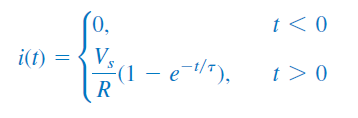
یا
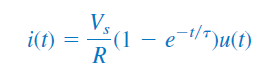
معادله بالا، پاسخ مدار در حالتی است که سلف از قبل انرژی نداشته باشد. ولتاژ سلف را میتوان از رابطه (36) و با استفاده از نوشت:
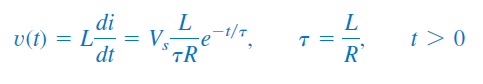
یا
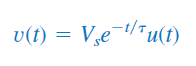
شکل ۱۳، نمودار جریان و ولتاژ سلف را نشان میدهد.
جدای از عملیاتی که برای بهدست آوردن جریان یک سلف انجام شد، یک روش نظاممند یا به تعبیر بهتر، میانبُر برای یافتن پاسخ پله یک مدار RL وجود دارد. مشخص است که دو بخش دارد. دو راه برای تفکیک این دو بخش وجود دارد. راه اول، جدا کردن پاسخ به دو بخش «پاسخ طبیعی و پاسخ اجباری» و راه دوم، جدا کردن به دو بخش «پاسخ گذرا و پاسخ حالت ماندگار» است.
پاسخ کامل یک مدار را میتوان بهصورت زیر بیان کرد:

راه دیگر بیان پاسخ کامل، جدا کردن آن به دو بخش موقت و دائمی است:

پاسخ گذرا، موقتی است و بخشی از پاسخ است که با میل کردن زمان به بینهایت، مقدار آن به صفر میرسد. پاسخ حالت ماندگار نیز، آن بخش از پاسخ است که پس از از بین رفتن پاسخ گذرا باقی میماند.
روش تفکیک نخست برای پاسخ کامل، بر اساس منبع پاسخ است، درحالی که روش دوم، مبتنی بر دوام پاسخها است. در شرایط معین، پاسخ طبیعی و گذرا مشابه هستند. در نتیجه میتوان گفتن که پاسخ اجباری و حالت ماندگار نیز برابر خواهند بود.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- آموزش مبانی مهندسی برق 1
- دو قطبی در مدارهای الکتریکی — به زبان ساده
- تزویج در مدارهای الکتریکی — مفاهیم اصلی
^^













سلام و خسته نباشید
ببخشید درسوالی که درویدیو اول حل کردید چرا در سادیکو جواب متفاوتی قرار دادع و جواب آخرو 10e به توان منفی 2/3 در آورده
جواب شما کاملا برای من قانع کنندع بود و درست نفهمیدم چرا جواب شما و جواب سادیکو متفاوت هستش ؟
sadiku page 245 \\ example 7.3
دمتون گرم اجرتون با خدا