روش عقبگرد در طراحی الگوریتم – به زبان ساده

در این مقاله، ایده الگوریتم عقبگرد (Backtracking) مورد بررسی قرار می‌گیرد. روش عقبگرد یک الگوریتم جستجوی ساختاریافته به شمار می‌رود که با استفاده از یک درخت فضای حالت همه راه‌حل‌های ممکن را می‌یابد. در این مقاله سعی شده است که به ساده‌ترین روش و همراه با چند مسئله معروف و کاربردی، روش عقبگرد در طراحی الگوریتم بیان شود. برای آشنایی و یادگیری این روش، مطالعه این مقاله پیشنهاد می‌شود.

روش عقبگرد در طراحی الگوریتم چیست؟

روش «عقبگرد» (Backtracking) یا همان «پس گرد» یک روش الگوریتمی و راه‌حل افزایشی (Incremental) برای حل مسائل به صورت بازگشتی به حساب می‌آید. هدف این روش الگوریتمی، دستیابی به تمام راه‌حل‌های یک مسئله است. این روش شامل ساخت مجموعه‌ای از تمام راه‌حل‌ها به صورت افزایشی می‌شود. از آن‌جایی که در روش عقبگرد یک مسئله دارای محدودیت‌هایی است، راه‌حل‌هایی که نتوانند به پاسخ مورد نظر برسند، حذف خواهند شد. روش عقبگرد از فراخوانی بازگشتی (Recursive Calling) برای یافتن یک راه‌حل به وسیله ایجاد گام به گام راه‌حل‌ها، همراه افزایش مراحل استفاده می‌کند. از الگوریتم عقبگرد زمانی برای حل مسائل استفاده می‌شود که دنباله‌ای از اشیاء موجود باشند و هر کدام از این اشیاء هدفی داشته باشند.

برای یافتن این راه‌حل‌ها از یک درخت جستجو (Search Tree) به نام درخت فضای حالت (State Space Tree) استفاده می‌شود. در درخت فضای حالت هر شاخه یک متغیر است و هر سطح یک راه‌حل را نشان می‌دهد. در طراحی الگوریتم به روش عقبگرد، روش جستجوی عمق اول (Depth First Search | DFS) مورد استفاده قرار می‌گیرد. روش جستجوی عمق اول دارای دو روش بازگشتی (Recursive) و غیربازگشتی (Iterative) است، اما در روش عقبگرد فقط از روش بازگشتی آن استفاده می‌شود. هنگامی که الگوریتم جستجوی عمق اول شروع به کاوش در راه‌حل‌ها می‌کند، یک تابع مرزی (Bounding Function) نیز اعمال می‌شود تا به کمک آن، روش عقبگرد بررسی کند که چه زمانی راه‌حل به جواب مناسب می‌رسد.

اگر راه‌حل مناسب بود، روش عقبگرد به جستجو ادامه می‌‌دهد و اگر راه‌حل مناسب نبود، شاخه حذف می‌شود و الگوریتم به سطح قبلی باز می‌گردد و به این روش نیز، هرس کردن (Pruning) می‌گویند. در بخش بعدی مقاله «روش عقبگرد در طراحی الگوریتم» برای درک بهتر روش عقبگرد، این الگوریتم همراه با یک مثال توضیح داده شده است.

مثال روش عقبگرد در طراحی الگوریتم

در این بخش برای درک بهتر، مثالی ساده برای توضیح تئوری این الگوریتم ارائه شده است. در این مثال سه حرف b ،a و c وجود دارند و هدف مرتب‌سازی این سه حرف به شرطی است که حرف c در کنار حرف a قرار نگیرد. طبق روش عقبگرد در طراحی الگوریتم، ابتدا، برای حل این مثال، درخت فضای حالت به وجود می‌آید و تمام راه‌حل‌های ممکن بررسی و پیدا می‌شوند و با محدودیت تعریف شده (حرف c در کنار حرف a قرار نگیرد) مورد مقایسه قرار می‌گیرند.

فیلم آموزش روش تقسیم و حل در طراحی الگوریتم – مرور و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

سپس فقط راه‌حلی باقی می‌ماند که طبق محدودیت تعریف شده در مثال، وجود داشته باشد. در شکل زیر درخت فضای حالت این مثال همراه با راه‌حل‌های موجود آن مشاهده می‌شود.

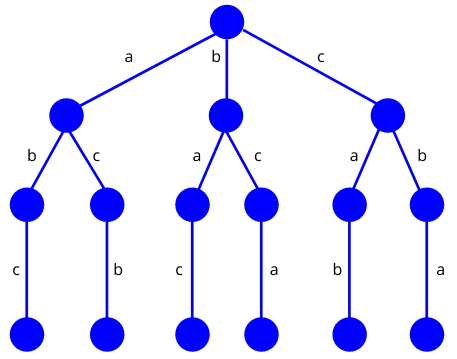
همه راه‌حل‌های ممکن برای مثال فوق به صورت زیر است:

$$(a,b,c), (a,c,b), (b,a,c), (b,c,a), (c,a,b) و (c,b,a)$$

با این وجود، راه‌حل‌های معتبر برای این مثال، راه‌حل‌هایی هستند که محدودیت سوال را طبق چیزی که نیاز دارند، بررسی و برآورده می‌کنند. بنابراین، تنها جواب‌های (a,b,c) و (c,b,a) به عنوان پاسخ نهایی در مجموعه جمع‌آوری شده باقی می‌مانند. در بخش بعدی این مقاله به این سوال پاسخ داده شده است که چه زمانی از روش عقبگرد در طراحی الگوریتم استفاده می‌شود.

چه زمانی از روش عقبگرد در طراحی الگوریتم استفاده می‌شود؟

روش عقبگرد برای همه مسائل نمی‌تواند اعمال شود و فقط برای انواع خاصی از مسائل مورد استفاده قرار می‌گیرد. به عنوان مثال، می‌توان از آن جهت یافتن یک راه‌حل ممکن برای یک مسئله تصمیم‌گیری (Decision problem) استفاده کرد. همچنین طبق بررسی‌های انجام شده، مشخص شده است که برای مسائل بهینه‌سازی (Optimization problems) نیز روش عقبگرد بسیار مؤثر عمل می‌کند.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

در برخی موارد، یک الگوریتم عقبگرد برای مسئله شمارش (Enumeration problem) به منظور یافتن مجموعه‌ای از تمام راه‌حال‌های ممکن در مسئله مورد استفاده قرار می‌گیرد. از سوی دیگر، روش عقبگرد در طراحی الگوریتم یک روش بهینه برای حل یک مسئله در نظر گرفته نمی‌شود و زمانی کاربرد دارد که راه‌حل مورد نیاز برای حل یک مسئله محدود به زمان نباشد. در بخش بعدی مقاله «روش عقبگرد در طراحی الگوریتم» به بررسی چند الگوریتم روش عقبگرد پرداخته شده است.

بررسی شیوه حل برخی از مسائل سازگار با روش عقبگرد در طراحی الگوریتم

مسائل زیادی وجود دارند که برای رسیدن به جواب بهینه و مناسب، خود از روش عقبگرد در طراحی الگوریتم استفاده می‌کنند. در این بخش به بررسی چند نمونه از این مسائل پرداخته شده است. ادامه این بخش به بررسی یکی از مسائل کلاسیک این روش یعنی حل مسئله «چند وزیر» (n-Queens) با الگوریتم عقبگرد اختصاص داده شده است.

حل مسئله چند وزیر با استفاده از روش عقبگرد در طراحی الگوریتم چگونه است؟

یک مثال کلاسیک برای توضیح روش عقبگرد در طراحی الگوریتم، مسئله چند وزیر به حساب می‌آید. این مسئله، برای اولین بار توسط «Max Bezzel»، شطرنج‌باز آلمانی در سال ۱۲۲۷ شمسی (۱۸۴۸ میلادی) پیشنهاد شد. با توجه به صفحه شطرنج با اندازه «n»، مسئله این است که وقتی روی یک صفحه شطرنج $$n \times n$$ قرار داریم، هیچ دو وزیری به یکدیگر حمله نکنند.

واضح است که برای حل این مسئله، باید ترتیب همه موقعیت‌های n وزیر در صفحه شطرنج پیدا شوند. اما یک محدودیت وجود دارد و آن این است که هیچ وزیری نباید بتواند به وزیر دیگری حمله کند، یعنی هیچ دو وزیری در یک سطر، ستون و یا قطر قرار نگیرند.

شبه کد مسئله چند وزیر با روش عقبگرد در طراحی الگوریتم

شبه کدی که برای روش عقبگرد در حل مسئله چند وزیر مورد استفاده قرار می‌گیرد، به صورت زیر است:

این مسئله با آرایه «[n]Q» و پارامتر «k» شروع شده است که اندیس (Index) اولین سطر خالی را نشان می‌دهد. موقعیت وزیرها در صفحه شطرنج $$n \times n$$ با استفاده از آرایه Q[1 .. n] ذخیره می‌شوند، یعنی جایی که Q[i] نشان می‌دهد کدام مربع در ردیف i دارای وزیر است. برای حل این مسئله، ابتدا سایز متغیر k بررسی می‌شود که بزرگتر از n باشد.

اگر این شرط برقرار باشد، آرایه Q[n] برگردانده می‌شود. اگر k کمتر از n باشد، موقعیت فعلی وزیر با مقدار اندیس بررسی می‌شود. اگر موقعیتی برای حمله دو وزیر به یکدیگر در صفحه شطرنج ایجاد نشود، اندیس در آرایه Q[n] ذخیره می‌شود. به این ترتیب، با فراخوانی بازگشتی تابع «()NQueen»، تمام موقعیت‌های صفحه شطرنج مورد بررسی قرار می‌گیرند.

یک مثال برای راه‌حل مسئله چند وزیر با روش عقبگرد در طراحی الگوریتم

اگر یک صفحه شطرنج $$n \times n$$ را به صورتی در نظر بگیریم که n برابر با ۵ باشد، با استفاده از ۱۰ راه‌حل می‌توان به جواب نهایی رسید. از روش عقبگرد برای بازیابی همه این راه‌حل‌ها استفاده می‌شود. خروجی روش عقبگرد تمام راه‌حل‌های ممکن برای این مسئله است که به ترتیب با چک کردن جایگاه هر وزیر در هر خانه به این خروجی می‌رسد.

فیلم آموزش طراحی الگوریتم – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

زمانی که حداقل دو وزیر در یک سطر، ستون و یا قطر قرار داشته باشند، پیمایش ادامه پیدا نمی‌کند و آن راه‌حل حذف می‌شود و به یک مرحله قبل بازمی‌گردد و زمانی که فقط یک وزیر در سطر، ستون و یا قطر وجود داشته باشد، پیمایش درخت فضای حالت برای رسیدن به جواب ادامه پیدا می‌کند. در تصویر زیر این صفحه شطرنج همراه با راه‌حل‌های ممکن آن برای مسئله چند وزیر ارائه شده است.

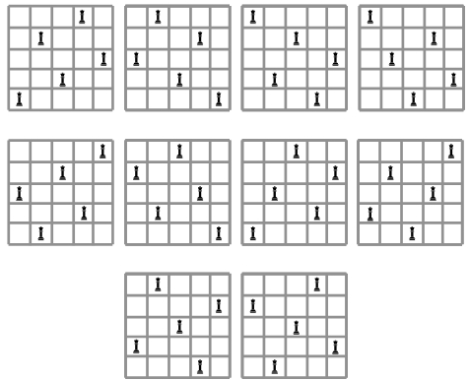
درست است که روش عقبگرد برای این مسئله، راه‌حل‌هایی معتبر پیدا می‌کند، اما همچنان، یک الگوریتم عقب‌گرد برای مسئله چند وزیر پیچیدگی زمانی برابر با $$O(2^n)$$ دارد. همان‌طور که پیش‌تر گفته شد، این روش برای مسائلی مناسب است که محدودیت زمانی نداشته باشند و راه‌حل‌ها و محدودیت‌ها برای آن‌ها مهم باشند. در ادامه بررسی انواع الگوریتم‌هایی که با استفاده از روش عقبگرد به جواب بهینه می‌رسند، به مسئله «حاصل جمع زیر مجموعه‌ها» (Subset Sum Problem) پرداخته شده است.

• مقاله پیشنهادی: حل مساله n وزیر با الگوریتم پس گرد (Backtracking) — به زبان ساده

حل مسئله حاصل جمع زیر مجموعه ها با استفاده از روش عقبگرد در طراحی الگوریتم چگونه است؟

در این بخش، حل مسئله حاصل جمع زیر مجموعه‌ها با استفاده از روش عقبگرد مورد بررسی قرار گرفته است. پیچیدگی زمانی در این روش نیز $$O(2^n)$$ است، اما با این حال استفاده از روش عقبگرد در این مسئله نسبت به رویکرد بازگشتی که پیچیدگی زمانی نمایی (Exponential Time) دارد، سریع‌تر است. در مسئله حاصل جمع زیرمجموعه‌ها هدف یافتن زیر مجموعه‌ای است که مجموع عناصر آن برابر با یک عدد معین باشد.

در بدترین حالت، روش عقبگرد در این مسئله همه جایگشت‌های (Permutation) ممکن را تولید می‌کند، اما به طور کلی، بهتر از روش بازگشتی عمل می‌کند. در این مسئله، مجموعه «A» از «n» عدد صحیح مثبت و یک عدد نیز به عنوان مجموع مقادیر، ورودی‌های مسئله به حساب می‌آیند. رویکرد حل این مسئله به این صورت است که باید بررسی شود آیا زیر مجموعه‌ای از مجموعه داده شده وجود دارد که جمع عناصر آن برابر با مقدار مجموع ورودی شود؟

یک مثال برای مسئله حاصل جمع زیر مجموعه ها

مجموعه زیر برای این مثال در نظر گرفته می‌شود:

{ 2, 9, 10, 1, 99, 3}

در این مسئله هدف این است که زیر مجموعه‌ای از این مجموعه بیابیم که مجموعه اعداد آن برابر با عدد چهار شود:

{ 1, 3 }

هدف دوم در نظر گرفته شده برای مسئله این است که زیر مجموعه‌ای بیابیم که مجموع اعداد آن برابر با پنج شود:

{ 2, 3}

و به همین تربیت، زمانی که مقدار مجموع عناصر زیرمجموعه برابر با شش باشد، زیرمجموعه زیر موجود است:

{2, 1, 3}

اما زمانی که مقدار مجموع عناصر زیرمجموعه برابر با عدد هفت باشد، هیچ زیرمجموعه‌ای با مجموع اعداد هفت وجود ندارد. این مسئله با سه روش از جمله روش عقبگرد، روش بازگشتی و برنامه نویسی پویا قابل حل است که در این مقاله روش عقبگرد برای حل این مسئله توضیح داده می‌شود.

حل مسئله حاصل جمع زیر مجموعه ها با استفاده از روش عقبگرد در طراحی الگوریتم

‌در الگوریتم عقبگرد همان‌طور که پیمایش در امتداد عمق درخت به سمت پایین انجام می‌گیرد، عناصر اضافه می‌شوند و اگر مجموع اضافه شده محدودیت‌های مورد نظر را برآورده کند، تولید گره‌های فرزند ادامه پیدا خواهند کرد. هر زمان که محدودیت‌ها برآورده نشدند، تولید بیشتر زیردرخت‌های (Sub-Tree) آن گره متوقف می‌شود و به گره قبلی بازمی‌گردد تا گره‌هایی که هنوز بررسی نشده‌اند، مورد بررسی قرار بگیرند.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

گره‌ها باید در امتداد عرض و عمق درخت کاوش شوند. تولید گره‌ها در امتداد عرض توسط حلقه (Loop) انجام می‌گیرد و گره‌ها در امتداد عمق با استفاده از روش بازگشتی (post order traversal | نمایش پس ترتیب) تولید می‌شوند.

مراحل حل مسئله حاصل جمع زیر مجموعه ها با استفاده از روش عقبگرد در طراحی الگوریتم

در این بخش هر یک از گام‌های حل مسئله حاصل جمع زیر مجموعه ها با استفاده از روش عقبگرد فهرست شده‌اند:

1. حل مسئله با یک زیر مجموعه خالی شروع می‌شود.
2. عنصر بعدی از فهرست به مجموعه اضافه می‌شود.
3. اگر زیر مجموعه دارای مجموع مقادیر M است، سپس ادامه پیمایش آن زیر مجموعه به عنوان راه‌حل متوقف خواهد شد.
4. اگر جواب مناسب در زیرمجموعه به دست نیامد و یا اگر پیمایش مجموعه به پایان رسید، زیر مجموعه را به عقب پیمایش می‌کنند تا زمانی که مناسب‌ترین مقدار پیدا شود.
5. اگر زیر مجموعه امکان‌پذیر باشد (یعنی مجموع عناصر زیر مجموعه کوچک‌تر از مقدار M است.) پیمایش درخت به مرحله بعدی می‌رود.
6. اگر همه عناصر بدون یافتن زیر مجموعه مناسب پیمایش شدند و امکان عقبگرد نیز وجود نداشت، بدون ایجاد راه‌حل، آن قسمت از درخت متوقف می‌شود.

در ادامه این بخش به ارائه شبه کدی از روش حل مسئله حاصل جمع زیرمجموعه‌ها با روش عقبگرد ارائه شده است.

شبه کد مسئله حاصل جمع زیر مجموعه ها با استفاده از روش عقبگرد در طراحی الگوریتم

شبه کد مربوط به حل مسئله حاصل جمع زیر مجموعه‌ها با استفاده از روش عقبگرد در طراحی الگوریتم در ادامه آمده است:

void subset_sum(int list[], int sum, int starting_index, int target_sum) 
{ 
if( target_sum == sum ) 
{ 
subset_count++; 
if(starting_index < list.length)
subset_sum(list, sum - list[starting_index-1], starting_index, target_sum); 
} 
else
{ 
for( int i = starting_index; i < list.length; i++ ) 
{ 
subset_sum(list, sum + list[i], i + 1, target_sum); 
} 
} 
}

برای مثال مجموعه {1, 3, 2} وجود دارد و عدد ۳ برای مقدار عددی «M» به عنوان مجموع مقادیر زیر مجموعه‌ها در نظر گرفته می‌شود. پس این مسئله دارای دو خروجی {1, 2} و {3} است. مراحل بخش قبل برای حل این مسئله به صورت زیر بیان می‌شوند:

1. در ابتدا زیر مجموعه خالی {} در نظر گرفته می‌شود.
2. عدد اول مجموعه به عنوان عضوی از مجموعه اصلی به صورت {1} به زیر مجموعه خالی مرحله قبل اضافه می‌شود. (مجموع= ۱، ۱<۳)
3. عدد دوم مجموعه به صورت {۳, ۱} به زیر مجموعه مرحله قبل اضافه می‌شود (مجموع= ۴، ۳<۴، پس ادامه این پیمایش اشتباه است و به مرحله قبل بازمی‌گردد.)
4. پیمایش رو به عقب انجام می‌گیرد و عدد دوم مجموعه از زیر مجموعه مرحله قبل حذف می‌شود، پس اکنون زیر مجموعه به صورت {۱} است. (مجموع= ۱، ۱<۳.)
5. در این مرحله، عدد سوم مجموعه به زیر مجموعه اضافه می‌شود، پس اکنون زیر مجموعه به صورت {1, 2} است. (مجموع= ۳، ۳==۳، یکی از راه‌حل‌ها پیدا شد.)
6. سپس عدد اول و سوم مجموعه از زیر مجموعه حذف می‌شوند و عدد دوم مجموعه، به زیر مجموعه اضافه شده است و اکنون، زیر مجموعه‌ای به صورت {۳} ایجاد شده است. (مجموع= ۳، ۳==۳، راه‌حل دوم پیدا شد.)

حل مسئله رنگ آمیزی گراف با استفاده از روش عقبگرد در طراحی الگوریتم چگونه است؟

در مسئله رنگ‌آمیزی گراف، یک گراف وجود دارد و مسئله این است به این صورت است که همه رأس‌ها به تعداد «M» رنگ داده شده رنگ‌آمیزی شوند، به گونه‌ای که رنگ هیچ دو رأس مجاوری یکسان نباشد. برای نمونه، گراف زیر در نظر گرفته شده است.

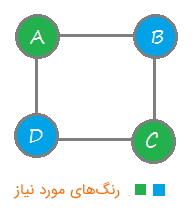
در این مسئله، تمام رأس‌هایی را می‌توان با رنگ‌های داده شده رنگ‌آمیزی کرد، سپس نتیجه رنگ‌آمیزی در خروجی ارائه می‌شود، در این صورت ممکن است راه‌حلی به عنوان خروجی وجود نداشته باشد. مسئله رنگ‌آمیزی گراف با روش الگوریتم ساده (Naive Algorithm) و روش عقبگرد مورد بررسی قرار می‌گیرد و قابل حل است که در این بخش از مقاله به بررسی این مسئله با روش عقبگرد پرداخته می‌شود.

حل مسئله رنگ آمیزی گراف با استفاده از روش عقبگرد در طراحی الگوریتم

استفاده از روش عقبگرد در طراحی الگوریتم برای حل مسئله رنگ‌آمیزی گراف (Graph Coloring Solution)، با اجتناب از بسیاری از تصمیمات نامناسب در رویکردهای ساده، فرآیند را کارآمد می‌کند. در این روش، ابتدا یک رأس و سپس رأس مجاور یا متصل به آن با رنگ متفاوتی رنگ‌آمیزی می‌شود.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

پس از آن مجدداً رنگ‌آمیزی رأس مجاور بعدی به رنگ قبلی انجام می‌شود و همین رویکرد ادامه دارد تا زمانی که همه راس‌ها رنگ‌‌آمیزی شوند. در صورتی که رأس‌هاییی پیدا شوند که تمام رأس‌هایی مجاور آن‌ها رنگی باشند و رنگی برای تغییر رنگ آن باقی نمانده باشد، درخت رو به عقب پیمایش و آخرین رأس رنگی آن تغییر رنگ داده می‌شود و سپس دوباره پیمایش رو به جلو ادامه پیدا می‌کند.

اگر با عقب نشینی به رأسی که از آن‌جا پیمایش شروع شده بود، متوجه این موضوع شوند که همه رنگ‌ها روی رأس‌هایی امتحان شده‌اند، به این معنی است که تعداد رنگ‌های داده شده (یعنی M) برای رنگ‌آمیزی گراف کافی نیست و به رنگ‌های بیشتری (یعنی یک عدد رنگ بزرگتر) نیاز است.

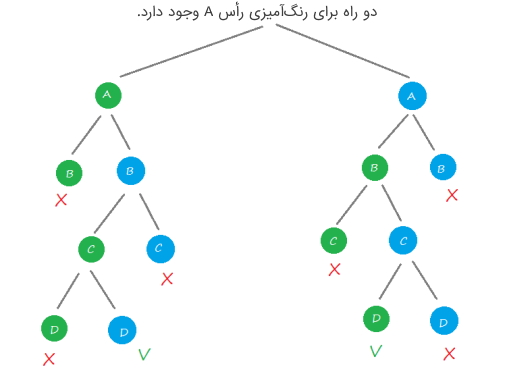
مراحل مسئله رنگ‌آمیزی گراف با استفاده از روش عقبگرد در طراحی الگوریتم

1. رنگ‌های متفاوت:
   1. بررسی اینکه امکان رنگ‌آمیزی رأس مورد نظر با رنگ فعلی وجود دارد (همراه با بررسی اینکه آیا هر یک از رأس‌هایی مجاور آن با همان رنگ رنگ‌آمیزی شده است).
   2. اگر رنگ متفاوت بود، پس رأس رنگ‌آمیزی می‌شود، در غیر این صورت باید رنگ دیگری امتحان شود.
   3. بررسی اینکه آیا همه رأس‌هایی رنگ‌آمیزی شده‌اند.
   4. اگر همه رأس‌هایی رنگ‌آمیزی نشده‌اند، رأسی که رنگ‌آمیزی نشده، رنگ می‌شود.
2. اگر هیچ رنگی برای رنگ‌آمیزی وجود نداشت، پیمایش رو به عقب انجام می‌گیرد.

در مسئله رنگ‌آمیزی گراف، روش عقبگرد به معنای متوقف کردن فراخوانی‌های بازگشتی بیشتر در رأس‌هایی مجاور به وسیله بازگشت‌های اشتباه است. مراحل اول (ادامه) و دوم (عقبگرد) این الگوریتم، باعث می‌شوند مسئله گزینه رنگ‌های مختلف را امتحان کند. مرحله «ادامه» (Continue) به معنی امتحان کردن رنگ‌های گوناگون برای رأس فعلی است و در مرحله «عقبگرد» (Backtrack) رنگ‌های گوناگون برای رأس رنگی آخر امتحان می‌شوند. در ادامه مقاله، به بررسی مثالی از مسئله مدار همیلتونی با الگوریتم عقبگرد پرداخته شده است.

حل مسئله مدار همیلتونی با استفاده از روش عقبگرد در طراحی الگوریتم چگونه است؟

در این مسئله با توجه به یک گراف «G = (V, E)» باید مدار همیلتونی با استفاده از روش عقبگرد پیدا شود. جستجو برای حل این مسئله از هر رأس دلخواه مانند «a» شروع می‌شود و این رأس به عنوان ریشه درخت ضمنی در نظر گرفته شده است. اولین عنصر از حل مسئله، اولین رأس میانی چرخه همیلتونی است که ساخته خواهد شد.

رأس بعدی بر اساس حروف الفبا انتخاب می‌شود. اگر در هر مرحله یک رأس دلخواه با هر رأسی به غیر از رأس «a» که ریشه گراف در نظر گرفته شد، چرخه‌ای بسازد، یعنی مسئله به بن‌بست (Dead end) رسیده است. در این حالت، مسئله یک مرحله به عقب برمی‌گردد، دوباره جستجو با انتخاب یک رأس دیگر آغاز می‌شود و راه‌حل قبلی باید حذف شود.

جستجو با استفاده از روش عقبگرد در طراحی الگوریتم، در صورتی موفقیت‌آمیز است که یک چرخه همیلتونی (Hamiltonian Cycle) به دست آید. در ادامه این بخش از مقاله به بررسی مثالی از مسئله مدار همیلتونی با استفاده از روش عقبگرد پرداخته شده است.

• مقاله پیشنهادی: گراف همیلتونی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

مثالی از مسئله مدار همیلتونی با استفاده از روش عقبگرد در طراحی الگوریتم

گراف G = (V, E) زیر در نظر گرفته شده است و در این بخش با استفاده از روش عقبگرد یک چرخه همیلتونی ایجاد می‌شود.

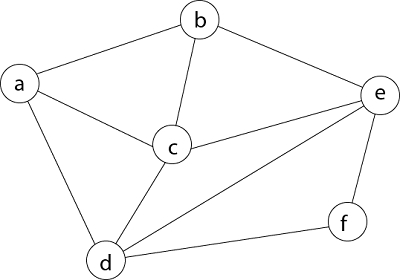
برای حل این مسئله با استفاده از روش عقبگرد، ابتدا یکی از رأس‌هایی به عنوان ریشه درخت صریح در نظر گرفته می‌شود. در این مثال، رأس «a» به عنوان ریشه است.

پس از آن، رأس «b» به عنوان رأس مجاور «a» انتخاب می‌شود زیرا در ترتیب واژگان حروف الفبا به صورت (b, c, d)، رأس «b» اول قرار گرفته است.

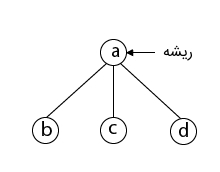
سپس، به عنوان رأس مجاور «b»، رأس «c» انتخاب می‌شود.

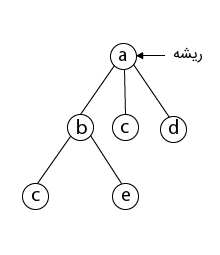
در مرحله بعد، رأس «d» در مجاورت رأس «c» انتخاب شده است.

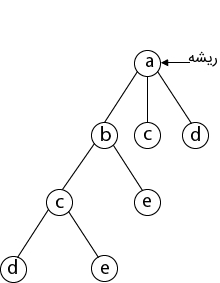
در این مرحله رأس «e» در مجاورت رأس «d» انتخاب می‌شود.

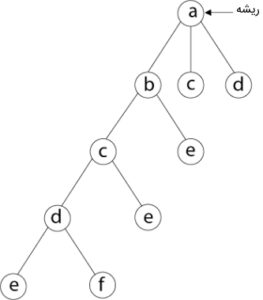
سپس، رأس «f» در مجاورت رأس «e» انتخاب می‌شود. رأس «f» در مجاورت رأس «d» و «e» در گراف مسئله قرار دارد، اما چون که آن دو رأس قبلاً بازدید شده‌اند پس در این قسمت راه‌حل مسئله به بن‌بست برخورد کرده است، بنابراین یک مرحله به قبل، عقبگرد انجام می‌گیرد و رأس «f» از گراف راه‌حل حذف می‌شود.

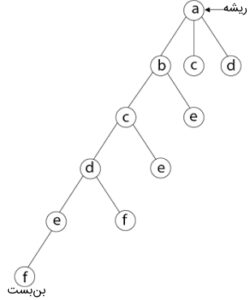
در روش عقبگرد این مسئله، مشاهده می‌شود که رأس مجاور «e» در این مرحله «b ،c ،d ،f» است که رأس «f» قبلاً بررسی شده است، و «b ،c ،d» نیز قبلاً در پیمایش درخت بازدید شده‌اند. بنابراین، دوباره یک قدم بازگشت به عقب انجام می‌شود. حال، رأس مجاور «d»، رأس‌هایی  «e , f» هستند که قبلاً بررسی شده‌اند، و رأس مجاور «f»، رأس‌هایی «d و f» هستند. اگر رأس «f»، مجدداً آن‌ها را بازدید کند، بن‌بست ایجاد می‌شود، پس دوباره یک مرحله عقبگرد انجام شده است. حال در این مرحله، رأس مجاور «c»، رأس «e»، رأس مجاور «e»، رأس «f»، رأس مجاور «f»، رأس «d» و رأس مجاور «d»، رأس «a» است. پس در این مرحله، چرخه همیلتونی دریافت می‌شود، زیرا تمام رأس‌های غیر از رأس ریشه «a» فقط یک بار بازدید شده‌اند.

در این مثال با استفاده از روش عقبگرد در طراحی الگوریتم، یک مدار همیلتونی تولید شد، اما با در نظر گرفتن یک رأس دیگر نیز می‌توان مدار همیلتونی دیگری به دست آورد. در بخش بعدی این مقاله به مسئله «کوله‌پشتی ۰ و ۱» پرداخته شده است.

• مقاله پیشنهادی: یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده

حل مسئله کوله پشتی صفر و یک با استفاده از روش عقبگرد در طراحی الگوریتم چگونه است؟

زمانی که از روش عقبگرد برای حل یک مسئله استفاده می‌شود، فضای حالت مسئله باید به صورت کاملاً واضح تعریف شود.

فیلم آموزش طراحی الگوریتم – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

فضای حالت مسئله، حداقل یک راه‌حل بهینه برای مسئله ایجاد می‌کند. برای مسئله کوله‌پشتی صفر و یک (0/1 knapsack problem) زمانی که «n=3» است، یک درخت جستجوی دودویی (Binary Search Tree| BST) جهت نشان دادن فضای حالت مسئله مانند تصویر زیر ایجاد می‌شود.

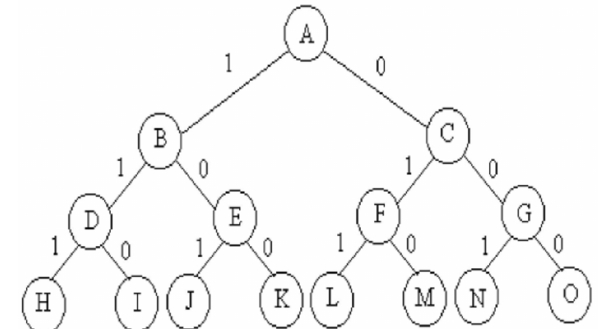
مراحل راه‌حل مسئله کوله‌پشتی صفر و یک به وسیله روش عقبگرد در طراحی الگوریتم

1. ابتدا برای مسئله کوله‌پشتی صفر و یک، فضای حالت مسئله تعریف می‌شود.
2. ساختار فضای حالت باید طوری تعریف شود که جستجو در آن ساده باشد.
3. فضای حالت مسئله با استفاده از یک الگوریتم عمقی جستجو می‌شود و یک تابع هرس (Pruning Function) برای جلوگیری از جستجوهای نامعتبر در طول جستجو مورد استفاده قرار می‌گیرد.

معمولاً در استفاده از تابع هرس، از تابع محدودیت (Constraint Function) برای حذف زیر درختانی (Subtrees) استفاده می‌شود که محدودیت‌های مسئله را برآورده نمی‌کنند و جواب بهینه‌ای برای مسئله به وجود نمی‌آوردند. روش عقبگرد برای حل مسئله کوله پشتی 0/1 درخت فضای حالت را تا زمانی جستجو می‌کند که چپ‌ترین گره آن یک گره امکان‌پذیر باشد. جستجوی زیر درخت سمت راست زمانی انجام می‌شود که این زیر درخت حاوی راه‌حل بهینه باشد. در غیر این صورت، زیر درخت سمت راست حذف می‌شود.

به این ترتیب در این مقاله سعی شد تا حد امکان به طور جامع به آموزش روش عقبگرد در طراحی الگوریتم پرداخته و همچنین مباحث پیرامون آن از جمله بررسی چند مسئله کاربردی انجام شود. اکنون در بخش پایانی این مقاله، برای آشنایی بیش‌تر و آموزش روش عقبگرد در طراحی الگوریتم، آن دسته از دوره‌های فرادرس که بیش‌ترین ارتباط را با روش عقبگرد در برنامه نویسی دارند به علاقه‌مندان معرفی شده‌اند.

فیلم مجموعه آموزش مهندسی و علوم کامپیوتر – جامع و کاربردی در فرادرس

کلیک کنید

جمع‌بندی

در این مقاله، ایده کلی روش عقبگرد در طراحی الگوریتم مورد بحث قرار گرفت. همچنین چند مسئله مهم ارائه شدند که حل آن‌ها با استفاده از روش عقبگرد به جواب‌های مطلوبی منجر می‌شود. روش عقبگرد در طراحی الگوریتم، یک ابزار معتبر و اساسی برای حل انواع مختلف مسائل است.

علی‌رغم اینکه این الگوریتم پیچیدگی زمانی بالایی دارد، باز هم یکی از گزینه‌هایی است که به دلیل داشتن راه‌حل‌های بهینه مناسب، مورد استفاده قرار می‌گیرد. زیرا ممکن است نیاز به بررسی همه راه‌حل‌های موجود همراه با مسیر ایجاد آن‌ها در یک مسئله وجود داشته باشد.