گراف همیلتونی — به زبان ساده
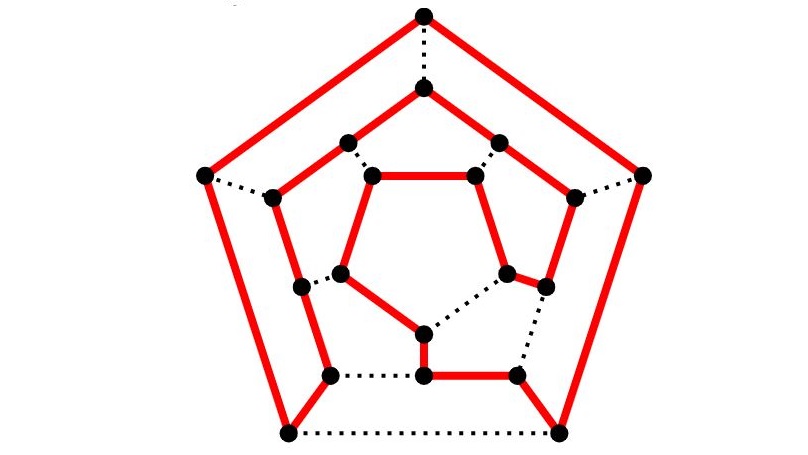
در آموزشهای قبلی مجله فرادرس، درباره گراف اویلری بحث شد. در این آموزش، قصد داریم گراف همیلتونی را بررسی کنیم.
گراف همیلتونی، به افتخار ریاضیدان ایرلندی «سر ویلیام همیلتون» (Sir William Hamilton)، به این نام شناخته میشود. او یک پازل اختراع کرد که به نام «بازی ایکوسیان» (Icosian Game) شناخته میشود. پازل همیلتون، یک دوازده وجهی است که هر روی هر ۲۰ رأس آن، نام یکی از شهرهای بزرگ جهان قرار داده شده است. هدف بازی این است که با عبور فقط یک بار از هر شهر، از همه شهرها عبور کنیم و دوباره به شهر اول بازگردیم.
گراف همیلتونی
در آموزش مربوط به گراف اویلری، درباره این موضوع صحبت کردیم که آیا میتوان در گراف همبند $$G$$ یک مسیر بسته یا دور پیدا کرد که همه یالها را طی کند. سوال مشابه این است که آیا میتوان یک مسیر بسته پیدا کرد که از همه رئوس گراف $$G$$، فقط یک بار عبور کند؟
مسیر یا گذر همیلتونی یا «مسیر قابل عبور» (Traceable Path) در یک گراف، به مسیری گفته میشود که از هر رأس گراف، فقط یک بار عبور کند. گرافی که یک مسیر همیلتونی داشته باشد، گراف «قابل قابل عبور» (Traceable Graph) نامیده میشود.
گذر بسته همیلتونی، دور همیلتونی نام دارد. دور همیلتونی یا مدار همیلتونی، مسیری است که از یک رأس شروع میشود و با گذر از همه رئوس مجددا به رأس اولیه بر میگردد. گرافی را که دور یا مدار همیلتونی داشته باشد، گراف همیلتونی مینامند.
در گراف همیلتونی، با شروع از یک رأس و عبور از بقیه رئوس باید مجددا به رأس اول رسید. در این حالت، عبور از همه یالها ضرورت ندارد اما عبور از همه رئوس ضروری است.
برای مثال، همه «اجسام افلاطونی» (Platonic Solids)، همیلتونی هستند. در شکل زیر، چند جسم افلاطونی نشان داده شده است:
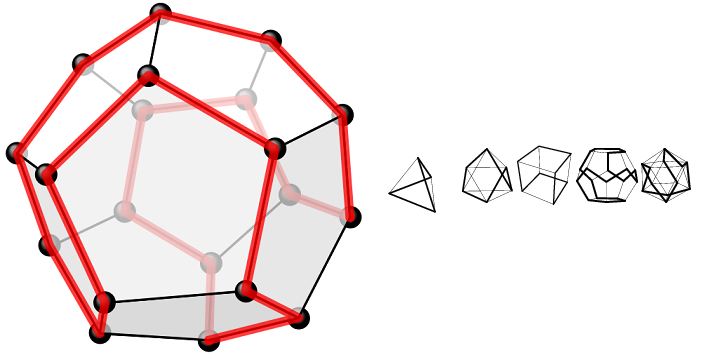
اجسام افلاطونی را میتوان به صورت دو بعدی و گراف مسطح زیر نمایش داد:
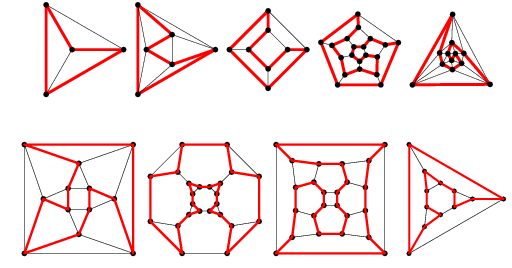
گراف غیر همیلتونی، به گرافی گفته میشود که نتوان با شروع از یک رأس از همه رئوس عبور کرد.
گراف شبه همیلتونی، یک گراف غیر همیلتونی است. در این گراف، با شروع از یک رأس و عبور از بقیه رئوس، به رأس اولیه باز نمیگردیم. گرافی که در آن یک گذر همیلتونی وجود دارد اما مدار همیلتونی ندارد، به نام گراف شبه همیلتونی شناخته میشود. در ادامه دو قضیه پرکاربرد از گراف همیلتونی بیان میشود:
- یک گراف کامل با بیشتر از دو رأس، همیلتونی است.
- هر گراف دوری، همیلتونی است.
خواص گراف همیلتونی
هر دور همیلتونی، با حذف یکی از یالها به مسیر همیلتونی تبدیل میشود. اگر در یک مسیر همیلتونی، رئوس آغازی و پایانی مجاور باشند، میتوان آن را به دور همیلتونی تعمیم داد. البته یک گراف غیر همیلتونی، ممکن است یک مسیر همیلتونی داشته باشد. بنابراین، مسیر همیلتونی، همیشه نشاندهنده وجود یک مدار همیلتونی نیست. برای مثال، شکل زیر را در نظر بگیرید:

گراف سمت راست، مسیر همیلتونی ندارد، پس دور همیلتونی نیز وجود نخواهد داشت. گراف میانی مسیر همیلتونی دارد، اما دور همیلتونی ندارد. در گراف سمت چپ، مسیر همیلتونی و دور همیلتونی وجود دارد.
اگر $$G$$ یک ٰگراف همیلتونی باشد، با اضافه کردن یال همچنان همیلتونی خواهد بود.
در آموزش قبلی مربوط به گراف اویلری، شروط لازم و کافی برای اویلری بودن یک گراف همبند را بیان کردیم. اما درباره گراف همیلتونی، نمیتوان شرط لازم و کافی را به دست آورد. در حقیقت، یکی از مسائل مهم حل نشده در نظریه گراف، پیدا نکردن شرط لازم و کافی برای همیلتونی بودن یک گراف است. به طور کلی، دانستههای زیادی درباره گراف همیلتونی وجود ندارد. بیشتر قضایای مربوط به گراف همیلتونی به این صورت است: اگر $$G$$ به تعداد کافی یال داشته باشد، $$G$$ همیلتونی است. مشهورترین این قضایا، «قضیه دیراک» (Dirac's theorem) است که از قضیه کلیتر «اوره» (Ore) استنتاج شده است.
قضیه اوره (Ore's Theorem): گراف ساده $$G$$ با حداقل سه رأس ($$n\geq 3$$) را در نظر بگیرید. اگر مجموع درجات رئوس غیر مجاور این گراف، بزرگتر یا مساوی تعداد رئوس باشد، آنگاه گراف $$G$$، همیلتونی است. یعنی:
$$deg(v)+deg(w) \geq n$$
که در آن، $$v$$ و $$w$$ هر جفت رأس غیر مجاور در این گراف است.
قضیه دیراک (Dirac's Theorem): اگر $$G$$، یک گراف ساده با حداقل سه رأس باشد و برای هر رأس $$v$$ داشته باشیم: $$deg(v) \geq n/2$$، آنگاه $$G$$ یک گراف همیلتونی است.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره سایر موضوعات مربوط به ریاضیات مطالب بیشتری یاد بگیرید، مطالب زیر به شما پیشنهاد میشوند:
^^










بسیار عالی بود ممنون
عالی بود
بسیار عالی بود مشکل من را کامل حل کرد از شما خیلی ممنونم