کسر متعارفی — به زبان ساده

کسر و کسر متعارفی، یک روش برای نمایش مقادیر در ریاضیات است. زمانی که از کسر برای نمایش یک مقدار استفاده می‌کنیم، در حقیقت مقدار یا نسبت چیزی را برحسب واحدی از چیز دیگر مشخص کرده‌ایم. بنابراین کسرها (Fraction) یک نسبت یا تقسیم را نشان می‌دهند. نوع خاصی از کسرها که صورت و مخرج آن اعداد صحیح باشند، کسر متعارفی (Simple Fraction) است که می‌تواند به صورت یک عدد گویا (Rational Number) بیان شود. در نتیجه کسرهای متعارفی متعلق به مجموعه اعداد گویا (Rational Number Set) هستند.

در این نوشتار به معرفی کسر متعارفی پرداخته و خصوصیات و نحوه محاسبه چهار عمل عصلی روی آن‌ها را معرفی می‌کنیم. به منظور آشنایی بیشتر با این گونه اعداد بهتر است نوشتارهای  قواعد بخش پذیری یا عاد کردن — به زبان ساده و تقسیم عدد صحیح — به زبان ساده را مطالعه کنید. همچنین خواندن متن اعداد حقیقی — به زبان ساده و اعداد گویا — به زبان ساده نیز خالی از لطف نیست.

کسر متعارفی

همانطور که در بالا اشاره کردیم، کسر متعارفی، نوع خاصی از انواع کسرها است که در بسیاری از محاسبات علمی و حتی روزمره به کار می‌رود.

برای مثال، فرض کنید قرار است کیکی را بین چهار نفر تقسیم کنیم. در این جا یک کیک را به صورت چهار قسمت مساوی، بخش‌بندی می‌کنیم. هر قسمت از این کیک بخشی است که به هر نفر خواهد رسید. در نتیجه سهمی از کیک که به هر یک از افراد می‌رسد را به صورت کسر متعارفی $$\frac{1}{4}$$ نشان می‌دهیم.

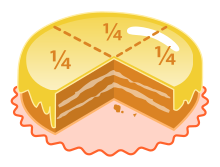
واضح است که کل بخش‌های کیک در مخرج کسر قرار گرفته و در صورت کسر نیز سهم هر نفر از بخش‌های تشکیل شده، ثبت می‌شود. از آنجایی که هم صورت و هم مخرج این کسر، عدد صحیح (Integer) است، آن را «کسر متعارفی» (Common or Vulgar Fraction) می‌گویند.

نکته: همه اعداد صحیح را می‌توان به صورت کسر متعارفی نشان داد.

$$\large 0 = \frac{0}{1},\;\;2= \frac{2}{1},\;\;-5=\frac{-5}{1},\ldots$$

تعریف کسر متعارفی

به عنوان یک تعریف رسمی از کسر متعارفی، گزاره زیر را می‌نویسند.

فرض کنید $$a$$ و $$b$$ دو عدد صحیح باشند که $$b\neq 0$$. در این صورت کسر $$\frac{a}{b}$$ را کسر متعارفی (Common Fraction) می‌گویند. به این ترتیب $$a$$ را صورت (Numerator) و $$b$$ را (Denominator) می‌نامند. گاهی به جای استفاده از علامت $$\frac{a}{b}$$ برای نمایش کسر از علامت $$a/b$$ نیز استفاده می‌کنند.

ممکن است مقدار $$a$$ یا $$b$$، مثبت یا منفی باشد ولی به هر حال کسر حاصل را متعارفی می‌گویند. برای مثال $$\frac{-5}{8}$$ یا $$\frac{5}{-8}$$ یا $$-\frac{5}{8}$$ همگی کسر متعارفی برابری هستند.

اگر صورت کسر متعارفی برابر با ۱ باشد می‌توان آن را به صورت توان منفی نیز نشان داد. برای مثال کسر $$\frac{1}{2}$$ را به صورت $$2^{-1}$$ نیز نشان می‌دهند. همچنین اعداد صحیح را به صورت کسر متعارفی با توان منفی نیز می‌توان مشخص کرد. برای مثال $$4=\frac{4}{1}=(\frac{1}{4})^{(-1)}$$ شیوه‌های مختلف نمایش مقدار ۴ هستند.

نکته: اگر $$b=0$$ باشد، کسر را نامعین می‌گویند، زیرا تقسیم بر صفر تعریف نشده است.

انواع کسر متعارفی

با توجه به ویژگی‌هایی که کسرهای متعارفی دارند آن ها را به دسته‌ یا گروه‌های مختلفی، طبقه‌بندی می‌کنند. در ادامه به معرفی بعضی از این کسرها و ویژگی‌های اصلی آن‌ها خواهیم پرداخت.

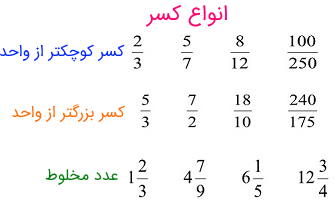
کسر بزرگتر از واحد و کوچکتر از واحد

کسر متعارفی $$\frac{a}{b}$$ را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم $$a>b$$، کسر از یک (واحد) بزرگتر است. در این صورت $$\frac{a}{b}$$ را کسر بزرگتر از واحد (Improper Fraction) می‌نامند. گاهی کسرهای بزرگتر از واحد را به صورت عدد مخلوط نشان می‌دهند. در ادامه این گونه اعداد نیز معرفی خواهند شد.

برعکس، اگر در کسر $$\frac{a}{b}$$ صورت از مخرج کوچکتر باشد، یعنی $$a$$، کسر را کوچکتر از واحد (Proper Fraction) می‌نامند. برای مثال $$\frac{4}{5}$$ کسر کوچکتر از واحد است.

نکته: توجه داشته باشید که اگر صورت و مخرج کسر متعارفی، برابر باشند، کسر نشانگر مقدار عدد صحیح واحد یا همان یک خواهد بود.

$$\large \frac{a}{a}=1,\;\;a \neq 0,\;\; \frac{5}{5}=1,\;\;\frac{56}{56}=1$$

کسر اعشاری و درصدی

کسر اعشاری، یک کسر متعارفی است که مخرج آن ۱۰ یا توانی از ۱۰ است. اغلب برای نمایش کسرهای اعشاری از علامت ممیز (٫) استفاده می‌شود. برای مثال کسر متعارفی $$\frac{1}{10}$$ را می‌توان به صورت ۰٫۱ نشان داد. همچنین کسر $$\frac{12}{20}$$ را می‌توان با ضرب صورت و مخرج در مقدار ۵ به صورت $$\frac{60}{100}$$ یا ۰٫۶۰ و حتی به طور خلاصه‌تر ۰٫۶ نشان داد.

کسرهای اعشاری را با نماد علمی (Scientific Notation) نیز می‌توان نشان داد. به این صورت یک رقم صحیح و بقیه ارقام به صورت اعشاری و برحسب توان‌هایی از ۱۰ مشخص می‌شوند. برای مثال عدد ۰٫6023 را به صورت $$6.023 \times 10^{-1}$$ با نماد علمی نشان می‌دهند.

برای نمایش اعداد اعشاری که دارای بی‌نهایت رقم تکرار شونده اعشار هستند، از کسر متعارفی استفاده می‌شود. برای مثال کسر متعارفی $$\frac{1}{3}$$ بیانگر مقدار ...۰٫۳۳۳۳ است. به بیان دیگر می‌توان این کسر را به صورت زیر نمایش داد:

$$\large \dfrac{1}{3}= \dfrac{3}{10}+\dfrac{3}{100}+\dfrac{3}{1000}+\ldots$$

در ادامه در مورد این گونه کسرها به کسرهای متناوب مشهور هستند صحبت خواهیم کرد.

اگر مخرج کسر قابل تبدیل به ۱۰۰ باشد می‌توان اعداد را به صورت درصدی (Percentage) یا به صورت نماد ٪ نیز نشان داد. برای مثال کسر متعارفی $$\frac{5}{100}$$ همان مقدار ۵٪ است و $$\frac{29}{100}$$ مقدار ۲۹٪ را نشان می‌دهد.

نکته: گاهی برای نمایش اعداد بسیار کوچک، به جای در نظر گرفتن ۱۰۰ قسمت برای مخرج کسر متعارفی، از هزار، ده هزار یا میلیون استفاده می‌کنند. برای مثال کسر $$\frac{75}{1000000}$$ را به صورت ۷۵ppm که مخفف «part per million» است مشخص می‌کنند.

کسر مولد اعشار مختوم و متناوب

همانطور که اشاره کردیم، کسر در حقیقت مشابه عمل تقسیم صورت بر مخرج است. به این ترتیب می‌توان کسرها را مولد اعداد اعشاری (یا صحیح) در نظر گرفت. بر اساس اینکه حاصل تقسیم کسر یک عدد با تعداد ارقام مشخص باشد، کسر را مولد اعشار مختوم یا متناوب می‌گویند. تشخیص اینکه کسر، مولد اعشار مختوم یا متناوب است بستگی به عوامل اول حاصل از تجزیه مخرج دارد.

نکته: محاسباتی که در ادامه مورد بحث قرار گرفته است، باید بعد از ساده‌کردن کسرها صورت گیرد.

کسر مولد اعشار مختوم

اگر با تقسیم صورت بر مخرج، به باقی‌مانده صفر برسیم، کسر را مولد اعشار مختوم می‌نامند. این حالت در زمانی رخ می‌دهد که مخرج کسر فقط شامل عامل‌های ۲ یا ۵ یا هر دو باشد.

برای مثال کسر $$\frac{6}{25}$$ مولد عدد اعشاری مختوم است، زیرا مخرج آن از عامل ۵ تشکیل شده.

$$\large \dfrac{6}{25}= 6 \div 25 = 0.24$$

همچنین کسر $$\frac{3/}{16}$$ نیز مولد عدد اعشاری مختوم است زیرا مخرج آن از عامل ۲ تشکیل شده.

$$\large \dfrac{3}{16}= 3 \div 16 = 0.1875$$

از طرفی کسر $$\frac{5}{20}$$ نیز که مخرج آن دارای فقط عامل‌های ۲ و ۵ است نیز یک کسر مولد اعشار مختوم است.

$$\large \dfrac{5}{20}= 5 \div 20 = 0.25$$

نکته: برای تبدیل این گونه اعداد اعشاری به کسر، کافی است صورت را برابر با رقم‌ها اعشار و مخرج را متناسب با تعداد رقم‌های اعشار به صورت توان‌هایی از ۱۰ بنویسیم.

برای مثال در عدد 0٫24 مقدار ۲۴ را در صوت کسر قرار داده و از آنجایی که دو رقم اعشار وجود دارد، مخرج را برابر با $$10^2$$ قرار می‌دهیم.

$$\large 0.24 = \frac{24}{100}$$

به همین ترتیب می‌توانیم دیگر کسرها را هم ایجاد کنیم.

$$\large 0.1875 = \frac{1875}{10000}=\frac{375}{2000}=\frac{75}{400}=\cdots=\frac{3}{16}$$

همچنین

$$\large 0.25=\frac{25}{100}= \frac{5}{20}$$

کسر مولد اعشاری متناوب

کسرهای هم وجود دارند که در آن‌ها حاصل تقسیم صورت بر مخرج، باقی‌مانده صفر نخواهند داشت. به این ترتیب عدد اعشاری حاصل، مختوم نخواهد بود.

برای مثال کسرهای $$\frac{1}{3}$$ یک عدد اعشاری با مقدار اعشار متناوب ایجاد می‌کند.

$$\large \frac{1}{3}= 0.33333\ldots$$

ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش می‌نامند. در نتیجه دوره گردش عدد بالا رقم ۳ است. همچنین

$$\large \frac{2}{3}= 0.6666\ldots$$

نیز به صورت صفر ممیز شش دوره گردش خوانده می‌شود.

نکته‌: معمولا ارقام گردش را به صورت یک خط بالای رقم گردش نشان می‌دهند. بنابراین داریم:

$$\large \frac{1}{3}= 0.33333\ldots=0.\bar{3}$$

یا

$$\large \frac{2}{3}= 0.6666\ldots=0.\bar{6}$$

از آنجایی که مخرج این گونه کسرها دارای عامل‌های اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقی‌مانده صفر نخواهند داشت. به این ترتیب کسرهای زیر نیز مولد اعشاری متناوب هستند.

$$\large \frac{1}{11}= 0.090909\ldots=0.\overline{09}$$

که آن را به صورت صفر ممیز، صفر نه، دوره گردش می‌خوانیم.

$$\large \frac{9}{11}= 0.818181\ldots=0.\overline{81}$$

که آن را به صورت صفر ممیز ۸۱ دوره گردش می‌خوانیم.

نکته: برای تبدیل یک عدد اعشاری متناوب به کسر متعارفی کافی است که ارقام دوره گردش را در صورت قرار داده و به تعداد ارقام دوره گردش در مخرج ۹ قرار دهیم. به مثال‌های زیر دقت کنید.

$$\large 0.\overline{3}=\frac{3}{9}=\frac{1}{3}$$

$$\large 0.\overline{6}=\frac{6}{9}=\frac{2}{3}$$

$$\large 0.\overline{09}=\frac{9}{99}=\frac{1}{11}$$

$$\large 0.\overline{81}=\frac{81}{99}=\frac{9}{11}$$

کسر مولد اعشاری متناوب مرکب

در این گونه کسرها، با تجزیه مخرج به عوامل اول به ارقام ۲ یا ۵ و یک یا چند عدد اول دیگر می‌رسیم. در این صورت عدد اعشاری شامل دو قسمت تکراری با گردش و بدون گردش خواهد بود.

برای مثال کسر $$\frac{8}{15}$$ از این گونه کسرها محسوب می‌شود، زیرا مخرج آن به عامل‌های ۵ و ۳ تجزیه می‌شود.

$$\large \frac{8}{15}= 0.5333\ldots=0.5\overline{3}$$

که آن را به صورت صفر ممیز ۵، ۳ دوره گردش می‌خوانیم. همچنین کسرهای زیر در این گروه قرار می‌گیرند.

$$\large \frac{2}{15}=0.13333\ldots=0.1\overline{3}$$

$$\large \frac{5}{6}=0.83333\ldots=0.8\overline{3}$$

نکته: برای تبدیل این اعداد اعشاری به کسر متعارفی باید ارقام گردشی را از کل ارقام گردشی و غیر گردشی کم کنیم و در صورت کسر قرار دهیم. مخرج کسر هم از ترکیب ۹ و صفر ساخته می‌شود. به این ترتیب با توجه به تعداد ارقام غیر گردشی صفر و بعد از آن به تعداد ارقام گردشی 9 قرار می‌دهیم. به مثال‌های زیر دقت کنید.

$$\large 0.5\overline{3}= 0.5333\ldots=\frac{53-5}{90}=\frac{48}{90}=\frac{8}{15}$$

$$\large 0.1\overline{3}=0.13333\ldots=\frac{13-1}{90}=\frac{12}{90}=\frac{4}{30}=\frac{2}{15}$$

$$\large 0.8\overline{3}=0.83333\ldots=\frac{83-8}{90}=\frac{75}{90}=\frac{15}{18}=\frac{5}{6}$$

معکوس کسر و کسر معکوس

کسر متعارفی $$\frac{a}{b}$$ را در نظر بگیرید که$$a ,b \neq 0$$ در این صورت با جابجا کردن صورت و مخرج، کسر جدیدی ساخته می‌شود که به آن معکوس کسر $$\frac{a}{b}$$ می‌گویند.

$$\large \frac{a}{b} \xrightarrow{\text{Reciprocals}} \frac{b}{a}$$

به این ترتیب کسر $$\frac{2}{3}$$ معکوس کسر $$\frac{3}{2}$$ است و برعکس. توجه داشته باشید که این دو کسر با یکدیگر برابر نیستند زیرا مخرج آن‌ها که تعداد بخش‌ها را نشان می‌دهد با یکدیگر متفاوت بوده از طرفی کسرها مضرب خاصی از یکدیگر نیز نیستند.

اعداد مخلوط و کسرهای متعارفی

معمولا کسرهایی متعارفی بزرگتر از ۱ را به صورت اعداد مخلوط نشان می‌دهند. در این حالت عدد مخلوط شامل یک قسمت عدد صحیح و یک کسر متعارفی کوچکتر از واحد است. قسمت عدد صحیح همان خارج قسمت تقسیم و صورت کسر، باقی‌مانده تقسیم و مخرج کسر متعارفی نیز مقسوم علیه خواهد بود. به یاد دارید که در تقسیم عدد صحیح، باقی‌مانده باید مثبت باشد.

$$\large \frac{x}{b} = a \frac{c}{b}; \;\; x = a\times b +c, c>0$$

برای مثال $$\frac{24}{5}$$ را توجه به اصول تقسیم عدد صحیح می‌توان به صورت زیر نمایش داد.

$$\large \frac{36}{5}=7\frac{1}{5}$$

زیرا براساس تقسیم عدد صحیح داریم:

$$\large 36= 5 \times 7 + 1$$

به این ترتیب $$7\frac{1}{5}$$ عدد مخلوط نامیده می‌شود. به مثال‌های زیر دقت کنید.

$$\large \frac{23}{4}=5\frac{3}{4}$$

زیرا

$$\large 23= 4 \times 5 + 3$$

همینطور

$$\large \frac{26}{15}=1\frac{11}{15}$$

زیرا

$$\large 26= 15 \times 1 + 11$$

نمایش کسر و اعداد مخلوط روی محور اعداد

محور اعداد، نقش مهمی در به تصویر کشیدن عدد‌ها دارد و درک بیشتری به آن‌ها می‌دهد. نحوه نمایش اعداد صحیح روی محور اعداد در نوشتار اعداد صحیح — به زبان ساده، توضیح داده شده ولی در اینجا قصد داریم کسرها و اعداد مخلوط را روی محور اعداد نمایش دهیم.

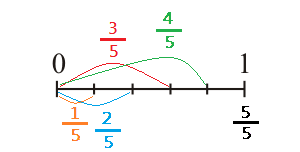
همانطور که گفته شد، مخرج هر کسر نشان‌دهنده تقسیماتی است که روی یک واحد صورت گرفته. از همین موضوع برای نمایش کسرها استفاده می‌کنیم. کافی است که برای نمایش کسر $$\frac{a}{b}$$ روی محور اعداد، یک واحد را روی این محور به $$b$$ قسمت مساوی تقسیم کنیم. حال برای نمایش کسر $$\frac{a}{b}$$ از نقطه صفر به تعداد $$a$$ واحد به سمت راست از این تقسیمات را می‌شماریم. محل مورد نظر کسر $$\frac{a}{b}$$ را نشان می‌دهد.

نکته: اگر مقدار $$a$$ منفی بود، باید شمارش را به سمت چپ محور انجام دهیم.

برای مثال کسرهای متعارفی با مخرج ۵ و صورت‌های ۱ تا ۵ به شکل زیر روی محور اعداد نمایش داده می‌شوند.

چهار عمل اصلی حساب روی کسر متعارفی

همانطور که برای اعداد صحیح، چهار عمل اصلی در حساب تعریف می‌شود، برای کسرهای متعارفی هم چهار عمل جمع، تفریق، ضرب و تقسیم قابل تعمیم است. در ادامه عملیات ریاضی که روی کسرهای متعارفی قابل اجرا است معرفی می‌شوند. قبل از معرفی چهار عمل اصلی برای کسرها، تساوی و رابطه بزرگتر و کوچکتر بین کسرها را مشخص می‌کنیم.

تساوی دو کسر

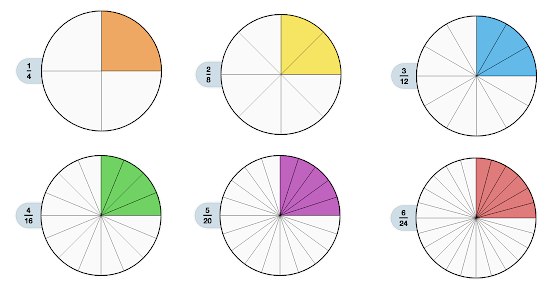
همانطور که گفته شد، مخرج کسر نشانگر تعداد قسمت‌هایی از یک واحد است. برای تصویر بالا، کیک (یک واحد) را به چهار قسمت تقسیم کردیم و ۱ واحد از آن را انتخاب کردیم. به این ترتیب کسر $$\frac{1}{4}$$ را شکل دادیم. به این ترتیب اگر تعداد تقسیم‌بندی‌ها را دو برابر کنیم، کیک به ۸ قسمت تقسیم شده و این بار دو قسمت از آن ۸ قسمت یعنی $$\frac{2}{8}$$ همان میزان کیک را نشان می‌دهد. بنابراین خواهیم داشت:

$$\frac{1}{4}=\frac{2}{8}$$

به این ترتیب مشخص می‌شود که اگر صورت و مخرج یک کسر را در مقدار ثابتی ضرب یا تقسیم کنیم، کسر تغییر نخواهد کرد. برای مثال کسرهای زیر همگی با هم برابر هستند.

$$\large \frac{1}{4}=\frac{2}{8}=\frac{3}{12}=\frac{4}{16}=\frac{5}{20}=\frac{6}{24}$$

مقایسه دو کسر

قبلا توضیح دادیم که دستگاه اعداد صحیح، دارای ترتیب است و می‌توان اعداد صحیح را دارای یک رابطه ترتیبی دانست. در اینجا هم برای کسرهای متعارفی رابطه ترتیبی را به کمک صورت و مخرج کسرها مشخص می‌کنیم.

برای این کار سه وضعیت را در نظر می‌گیرم.

• برابری مخرج کسرها: اگر دو کسر دارای مخرج یکسان باشند، کسری بزرگتر است که دارای صورت بزرگتری است.

$$\large \frac{a}{b};\;\;\;\; \frac{c}{b},\;\;b \neq 0\;\;\; \xrightarrow  {a \leq c} \frac{a}{b} \leq \frac{c}{b}$$

برای مثال کسر $$\frac{3}{5}$$ بزرگتر از کسر $$\frac{1}{5}$$ است.

• برابری صورت کسرها: اگر دو کسر دارای صورت یکسان باشند، کسری بزرگتر است که دارای مخرج کوچک‌تری است.

$$\large \frac{a}{b};\;\;\;\; \frac{a}{d},\;\;b,d \neq 0\;\;\; \xrightarrow  {b \leq d} \frac{a}{b} \geq \frac{a}{d}$$

برای مثال کسر $$\frac{3}{5}$$ بزرگتر از کسر $$\frac{3}{8}$$ است.

• نابرابری بین صورت و مخرج کسرها: در صورت که هیچ تساوی بین صورت یا مخرج کسرها برقرار نباشد، باید مخرج یا صورت کسرها را با ضرب یا تقسیم کردن کسرها در یک مقدار ثابت، یکسان کرده و به کمک روش‌های قبلی، مقایسه را انجام دهیم.

برای مثال برای سنجش رابطه ترتیبی بین دو کسر $$\frac{3}{5}$$ و $$\frac{4}{6}$$ به ترتیب زیر عمل می‌کنیم.

$$\large \frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}$$

$$\large \frac{4}{6}=\frac{4 \times 5}{6 \times 5}=\frac{20}{30}$$

حال با توجه به یکسان بودن مخرج کسرها، مشخص می‌شود که $$\frac{4}{6}$$ بزرگتر از $$\frac{3}{5}$$ است.

همچنین می‌توانستیم از یکسان سازی صورت کسرها نیز استفاده کنیم. به این ترتیب خواهیم داشت:

$$\large \frac{3}{5}=\frac{3 \times 4}{5 \times 4}=\frac{12}{20}$$

$$\large \frac{4}{6}=\frac{4 \times 3}{6 \times 3}=\frac{12}{18}$$

از آنجایی که مخرج کسر دوم کوچکتر است، پس نتیجه می‌گیریم که $$\frac{4}{6}$$ بزرگتر است.

جمع و تفریق دو کسر متعارفی

زمانی که دو کسر متعارفی قرار است با یکدیگر جمع شوند، دو حالت را در نظر می‌گیریم. ابتدا فرض می‌کنیم که مخرج یا در واقع واحد تقسیم هر دو کسر یکسان است. در ادامه حالتی را در نظر می‌گیریم که مخرج هر دو کسر با یکدیگر متفاوت بوده و قرار است عمل جمع را صورت دهیم.

جمع و تفریق دو کسر متعارفی با مخرج یکسان

فرض کنید دو کسر متعارفی با مخرج یکسان به صورت $$\frac{a}{b}$$ و $$\frac{c}{b}$$ قرار است با یکدیگر جمع یا تفریق شوند. واضح است که $$b\neq 0$$ است. برای بدست آوردن مجموع یا تفاضل این دو کسر به روش زیر عمل می‌کنیم.

ابتدا یک کسر با مخرج $$b$$ می‌سازیم و صورت را با جمع یا تفریق صورت دو کسر بدست می‌آوریم.

$$\large \frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$$

$$\large \frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}$$

برای مثال مجموعه دو کسر $$\frac{3}{5}$$ و $$\frac{4}{5}$$ برابر است با $$\frac{4+3}{5}=\frac{7}{5}$$.

جمع و تفریق دو کسر متعارفی با مخرج متفاوت

برای انجام جمع یا تفریق در این حالت باید کسرها را بوسیله ضرب یا تقسیم کردن صورت و مخرج‌ها در یک عدد، به شکلی درآوریم که مخرج کسرها یکسان شود. این روش به تکنیک جمع با مخرج مشترک، مشهور است.

فرض کنید قرار است کسر $$\frac{a}{b}$$ را با $$4\frac{c}{d}$$ جمع یا تفریق کنیم. مراحل کار به صورت زیر است.

1. کوچکترین مضرب مشترک (ک-م-م) بین $$b$$ و $$d$$ را پیدا می‌کنیم. فرض کنید آن را $$m$$‌ بنامیم. واضح است که $$m>b$$ و $$m>d$$ است.
2. حاصل تقسیم $$m$$ بر $$b$$ را بدست آورده و آن را $$x$$ می‌نامیم. همین کار را هم برای $$m$$ و $$d$$ انجام داده و نسبت آن‌ها را $$y$$ نام‌گذاری می‌کنیم.
3. صورت و مخرج کسر اول ($$\frac{a}{b}$$) را در $$x$$ و صورت و مخرج کسر دوم ($$\frac{c}{d}$$) را در $$y$$ ضرب می‌کنیم.
4. واضح است که مخرج‌ها یکسان خواهند شد. حال به حالت قبل جمع یا تفریق دو کسر با مخرج یکسان را بدست خواهیم آورد.

برای مثال حاصل جمع $$\frac{4}{9}$$ با $$\frac{5}{6}$$ توسط گام‌های زیر حاصل می‌شود.

1. کوچکترین مضرب مشترک بین مخرج دو کسر (یعنی ۶ و ۹) با توجه به تجزیه به عوامل اول برابر با ۱۸ خواهد بود.
   $$\large 6 = 2 \times 3 , \;\;\; 9 = 3 \times 3= 3^2$$
   پس کوچکترین مضرب مشترک از حاصل‌ضرب عوامل غیر مشترک در عوامل مشترک با بزرگترین توان نوشته می‌شود. $$m=2 \times 3^2=17$$
2. مقدار $$x$$ را برابر با $$x=18 \div 9=2$$ و $$y$$ را به صورت $$y=18 \div 6=3$$ بدست می‌آوریم.
3. صورت و مخرج کسرها را در مقادیر متناظر $$x$$ و $$y$$ ضرب می‌کنیم. $$\large \frac{2\times 4}{9 \times 2}=\frac{8}{18}, \;\;\frac{5 \times 3}{6 \times 3}=\frac{15}{18}$$
4. حاصل جمع را مطابق با روش قبلی (برابری مخرج کسرها) بدست می‌آوریم و در صورت امکان کسر را ساده می‌کنیم.

$$\large \frac{8}{18}+\frac{15}{18}=\frac{23}{18}$$

نکته: اگر مخرج دو کسر نسبت به یکدیگر اول (هم‌اول یا متباین) باشند، کوچکترین مضرب مشترک برای آن‌ها همان حاصل‌ضربشان خواهد بود.

برای مثال برای جمع کردن دو کسر $$\frac{2}{3}$$ و $$\frac{4}{5}$$ از آنجایی که ۵ و ۳ نسبت به یکدیگر اول هستند، مخرج مشترک برابر با ۱۵ خواهد بود. پس کافی است صورت و مخرج کسر اول را در ۵ و صورت و مخرج کسر دوم را در ۳ ضرب کنیم.

$$\large \frac{2}{3}+\frac{4}{5}=\frac{2 \times 5}{3 \times 5}+\frac{4\times 3}{5 \times 3}=\frac{10}{15}+\frac{12}{15}=\frac{22}{15}$$

حاصل ضرب و تقسیم دو کسر

حاصل ضرب دو کسر متعارفی، یک کسر متعارفی خواهد بود که صورت آن برابر با حاصل‌ضرب صورت‌ها و مخرج نیز برابر با حاصل‌ضرب مخرج‌ها است.

بنابراین اگر $$\frac{a}{b}$$ و $$\frac{c}{d}$$‌ دو کسر متعارفی باشند، بطوری که $$b \neq 0 , d \neq 0$$ آنگاه داریم:

$$\large \frac{a}{b}\times \frac{c}{d} = \frac{a \times c}{b \times d}$$

برای مثال حاصل‌ضرب دو کسر $$\frac{3}{5}$$ در $$\frac{5}{6}$$ برابر است با:

$$\large \frac{3}{5}\times \frac{5}{6} = \frac{3 \times 5}{5 \times 6}=\frac{15}{30}=\frac{1}{2}$$

نکته: از آنجایی که ضرب یا تقسیم صورت و مخرج کسر در مقدار ثابت، آن را تغییر نمی‌دهد، در تساوی آخر، هر دو صورت و مخرج را بر ۱۵ تقسیم کرده‌ایم. اگر $$n$$ را بزرگترین مقسوم علیه مشترک (ب-م-م) بین صورت و مخرج در نظر بگیریم، با تقسیم کردن این دو مقدار بر (ب-م-م)، کسر متعارفی ساده می‌شود.

عمل ساده‌کردن کسرها را قبل از انجام عملیات ضرب نیز می‌توانستیم انجام دهیم. با توجه به مثال بالا خواهیم داشت:

$$\large \frac{3}{5}\times \frac{5}{6} = \frac{\color{blue}{\not{3}^{1}}\times \color{red}{\not{5}^{1}}}{\color{red}{\not{5}_{1}} \times \color{blue}{\not{6}}_2}=\frac{1}{2}$$

همچنین برای تقسیم دو کسر متعارفی می‌توان آن را به صورت حاصل‌ضرب نوشت و عملیات را مطابق با عملیات ضرب انجام داد. برای این کار کافی است که کسر مقسوم علیه را به صورت معکوس در آورده و در مقسوم ضرب کنیم.

فرض کنید قرار است کسر $$\frac{a}{b}$$ را بر $$\frac{c}{d}$$ تقسیم کنیم. البته در اینجا باید شرط $$d \neq 0, \;c\neq 0 ,\; d \neq 0$$ را داشته باشیم. در این صورت حاصل تقسیم برابر است با:

$$\large \frac{a}{b}\div \frac{c}{d} = \frac{a}{b}\times \frac{d}{c}$$

زیرا اگر به جای تقسیم از علامت کسر استفاده کنیم، می‌توانیم بنویسیم:

$$\large \frac{a}{b}\div \frac{c}{d} = \dfrac{\frac{a}{b}}{\frac{c}{d}}=\dfrac{a \times d}{b \times c}=\frac{a}{b}\times \frac{d}{c}$$

این تکنیک به روش دور در دور، نزدیک در نزدیک معروف است.

برای مثال تقسیم کسر $$\frac{2}{3}$$ بر $$\frac{4}{5}$$ برابر است با:

$$\large \frac{2}{3}\div \frac{4}{5}=\frac{\color{blue}{\not{2}}^1}{3}\times  \frac{5}{\color{blue}{\not{4}_2}}=\frac{5}{6}$$

نکته: ضرب یک کسر در معکوس خودش برابر با ۱ خواهد بود. تقسیم یک کسر بر معکوسش نیز کسر را به صورت مربع در می‌آورد.

$$\large \frac{a}{b} \times \frac{b}{a} = 1, \;\;\; \frac{a}{b}\div \frac{b}{a}=\frac{a}{b}\times \frac{a}{b}= \frac{a^2}{b^2}$$

خلاصه و جمع‌بندی

در این نوشتار به بررسی کسرها و بخصوص کسر متعارفی پرداختیم. همچنین مقایسه و در نظر گرفتن ترتیب بین این گونه کسرها را مرور کردیم. ضمناً نحوه انجام چهار عمل اصلی برای کسرهای متعارفی را مورد بررسی قرار دادیم. بسیاری از عملیات تقسیم و حتی ضرب به کمک کسرهای متعارفی ساده‌تر صورت می‌گیرد. در نتیجه شناخت از این گونه کسرها هم به دامنه شناخت اعداد کمک می‌کند و هم محاسبات ریاضی را برایمان ساده‌تر می‌سازد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• تقسیم عدد صحیح — به زبان ساده
• اعداد حقیقی — به زبان ساده
• اعداد گویا — به زبان ساده
• اعداد مختلط – به زبان ساده

^^