دمدولاتور SSBSC — از صفر تا صد
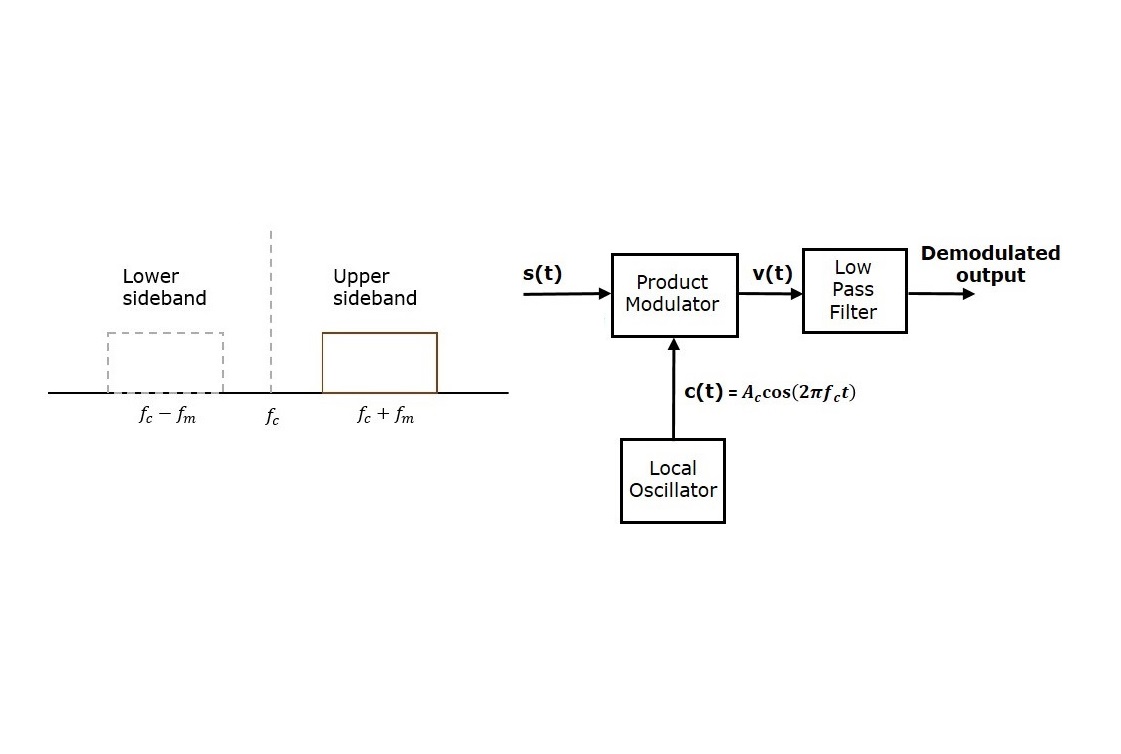
در مطالب قبلی مجله فرادرس به بیان تفاوتهای دو روش مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC و مدولاسیون حامل سرکوب شده باند جانبی تکی یا SSBSC پرداختیم. همچنین مدارات مدولاتور DSBSC و مدولاتور SSBSC را بررسی کردیم. در این مطلب قصد داریم مدار دمدولاتور SSBSC را معرفی کنیم و با اصول کار آن آشنا شویم.
در حالت کلی به فرایند استخراج یک سیگنال پیام اصلی از یک سیگنال مدولاسیون حامل سرکوب شده باند جانبی تکی یا SSBSC، آشکارسازی یا دمدولاسیون SSBSC میگویند. یکی از مهمترین و سادهترین مداراتی که به منظور دمدولاسیون SSBSC مورد استفاده قرار میگیرد، مدار «آشکارساز یا دمدولاتور همدوس» (Coherent Detector) است.
مدار دمدولاتور SSBSC با باند جانبی پایین
در یک مدار دمدولاتور SSBSC از یک سیگنال حامل برای فرایند دمدولاسیون و آشکارسازی استفاده میشود که دارای فرکانس و فاز یکسان با سیگنال حامل اصلی باشد که در مدار مدولاتور SSBSC برای تولید سیگنال به کار برده شده بود. دقیقا به همین دلیل است که به این روش دمدولاسیون، «آشکارسازی سنکرون» (Synchronous Detection) یا همدوس گفته میشود.
در تصویر زیر نمایش بلوک دیاگرامی از یک مدار دمدولاتور SSBSC نشان داده شده است.
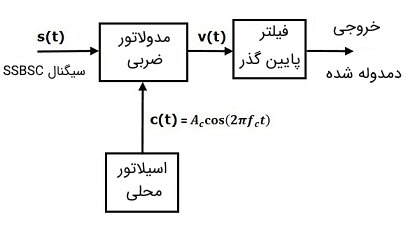
در فرایند دمدولاسیون یک سیگنال SSBSC، سیگنال پیام اصلی را میتوانیم از طریق ضرب کردن سیگنال مدولاسیون SSBSC در یک سیگنال حامل به دست آوریم. البته به این نکته توجه کنید که باید سیگنالی شبیه به سیگنال حامل اصلی را بازسازی و تولید کنیم که هم فاز و هم فرکانس با آن باشد. سیگنال حاصل از ضرب سیگنال مدولاسیون SSBSC در سیگنال حامل را به یک مدار فیلتر پایین گذر منتقل میکنیم. خروجی فیلتر پایین گذر همان سیگنال پیام است که قصد آشکارسازی آن را داشتیم. سیگنال مدولاسیون SSBSC زیر را در نظر بگیرید و فرض کنید که این سیگنال باند جانبی پایین داشته باشد. معادله سیگنال به صورت زیر نوشته میشود:
$$ s \left ( t \right ) = \frac { A _ m A _ c } { 2} \cos \left [ 2 \pi\left ( f _ c - f _ m \right ) t \right ] $$
همچنین سیگنال حاصل از اسیلاتور محلی را به صورت زیر در نظر بگیرید:
$$ c \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) $$
با توجه به بلوک دیاگرام فوق، سیگنال خروجی از «مدولاتور ضربی» (Product Modulator) به صورت زیر به دست میآید:
$$ v \left ( t \right ) = s \left ( t \right ) c \left ( t \right ) $$
حال با جایگذاری دو سیگنال $$ s \left ( t \right ) $$ و $$ c \left ( t \right ) $$ در رابطه فوق، میتوانیم خروجی مدولاتور ضربی را با رابطه ریاضی زیر نشان دهیم:
$$ v \left ( t \right ) = \frac { A _ m A _ c }{ 2 } \cos \left [ 2 \pi \left ( f _ c - f _ m \right ) t \right ] A _ c \cos \left ( 2 \pi f _ c t \right ) $$
$$ = \frac { A _ m { A _ { c} } ^ { 2 } } {2 } \cos \left [ 2 \pi \left ( f _ c - f _ m \right ) t \right ] \cos \left ( 2 \pi f _ c t \right ) $$
$$ = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \left \{ \cos \left [ 2 \pi \left ( 2 f _ c - f m \right ) \right ] + \cos\left ( 2 \pi f _ m \right ) t \right \} $$
$$ v \left ( t \right ) = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \cos \left ( 2 \pi f _ m t \right ) + \frac { A _ m{ A _ { c } } ^ { 2 } } { 4 } \cos \left [ 2 \pi \left ( 2 f _ c - f _ m \right ) t \right ] $$
در معادله به دست آمده در بالا، اولین عبارت یک نسخه مقیاس شده از سیگنال پیام اصلی است. برای اینکه در خروجی مدار فقط عبارت اول را داشته باشیم، باید سیگنال فوق را به یک فیلتر پایین گذر عبور دهیم. بنابراین معادله به دست آمده از خروجی فیلتر پایین گذر به صورت زیر نوشته میشود:
$$ v _ 0 \left ( t \right ) = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \cos \left ( 2 \pi f _ m t \right ) $$
همان طور که مشاهده میکنید، در خروجی فیلتر پایین گذر سیگنال پیام با فاکتور مقیاس $$ \frac { { A _ { c } } ^ { 2 } } { 4 } $$ به دست میآید.
مدار دمدولاتور SSBSC با باند جانبی بالا
از بلوک دیاگرام قسمت قبل میتوانیم برای دمدولاسیون یک سیگنال SSBSC با باند جانبی بالا نیز استفاده کنیم.
سیگنال زیر را در نظر بگیرید و فرض کنید که دارای باند جانبی بالا باشد:
$$ s \left ( t \right ) = \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c + f _ m \right ) t \right ] $$
خروجی مدار اسیلاتور محلی را به صورت زیر فرض کنید:
$$ c \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) $$
حال خروجی مدار مدولاتور ضربی را با ضرب کردن دو سیگنال $$ s \left ( t \right ) $$ و $$ c \left ( t \right ) $$ و جایگذاری مقادیر فوق به صورت زیر مینویسیم:
$$ v \left ( t \right ) = s \left ( t \right ) c \left ( t \right ) $$
$$ \Rightarrow v \left ( t \right ) = \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c + f _ m \right ) t \right ] A _ c \cos \left ( 2 \pi f _ c t \right ) $$
$$ = \frac { A _ m { A _ { c } } ^ { 2 } } { 2 } \cos \left [ 2 \pi \left ( f _ c + f _ m \right ) t \right ] \cos \left ( 2 \pi f _ c t \right ) $$
$$ = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \left \{ \cos \left [ 2 \pi \left ( 2 f _ c + f _ m \right ) t \right ] + \cos \left ( 2 \pi f _ m t \right ) \right \} $$
$$ v \left ( t \right ) = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \cos \left ( 2 \pi f _ m t \right ) + \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \cos \left [ 2 \pi \left ( 2 f _ c + f _ m \right ) t \right ] $$
اولین عبارت در معادله فوق، نسخه مقیاس شده سیگنال پیام مورد نظر ما است که قصد آشکارسازی آن را داشتیم. میتوانیم برای به دست آوردن ترم اول عبارت، سیگنال فوق را از یک فیلتر پایین گذر عبور دهیم. بنابراین سیگنال خروجی فیلتر پایین گذر به صورت زیر به دست میآید:
$$ v _ 0 \left ( t \right ) = \frac { A _ m { A _ { c } } ^ { 2 } } { 4 } \cos \left ( 2 \pi f _ m t \right ) $$
بر اساس معادله فوق مشاهده میکنیم که سیگنال پیام با یک ضریب مقیاس برابر با $$ \frac { { A _ { c } } ^ { 2 } } { 4 } $$ به دست میآید. بنابراین با استفاده از یک مدار دمدولاتور SSBSC همدوس میتوانیم سیگنال پیام را هم از سیگنال مدولاسیون SSBSC با باند جانبی بالا و هم از سیگنال مدولاسیون SSBSC با باند جانبی پایین به دست آوریم.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- دمدولاسیون دامنه — از صفر تا صد
- مدولاتور AM — از صفر تا صد
- حلقه قفل فاز (PLL) چیست؟ — از صفر تا صد
^^










