مدولاسیون DSBSC — از صفر تا صد
در مطالب قبلی از مجله فرادرس با مفهوم مدولاسیون و نیز روش مدولاسیون دامنه یا AM، مدولاسیون فاز یا PM و مدولاسیون فرکانس یا FM آشنا شدیم. همچنین دیدیم که با استفاده از روشهای مختلف دمدولاسیون دامنه میتوان یک سیگنال پیام را از سیگنال دریافتی در گیرنده بازیابی کرد. در این مطلب قصد داریم به بررسی یک روش مدولاسیون دامنه بپردازیم که با نام مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا مدولاسیون DSBSC شناخته میشود.
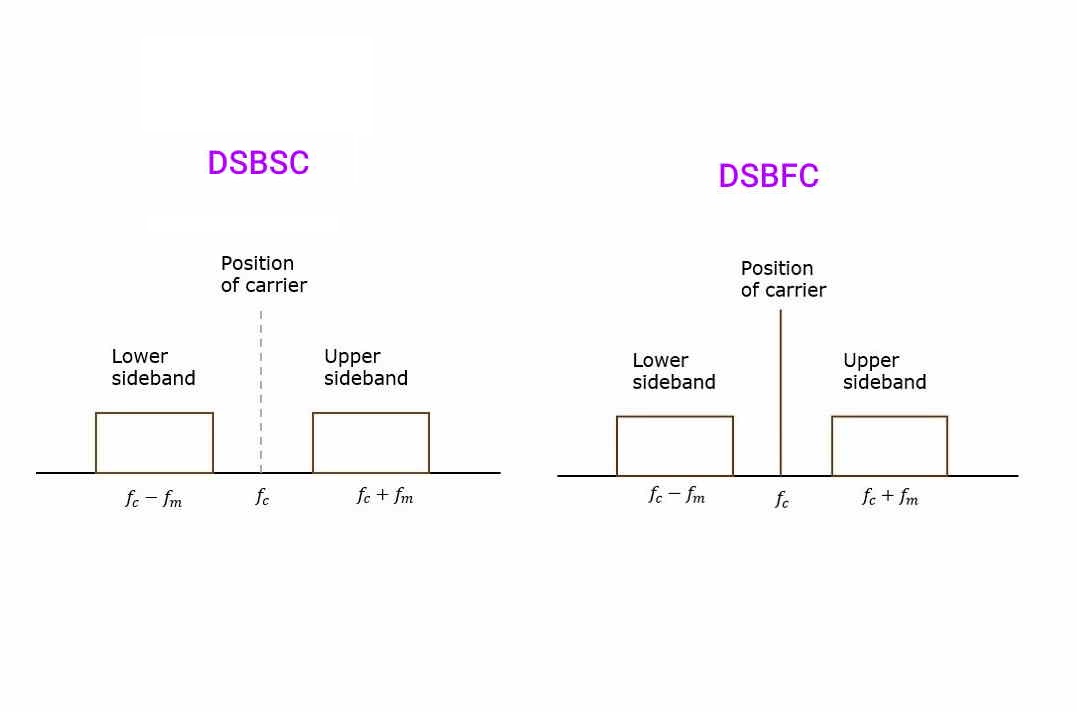
در فرایند مدولاسیون دامنه (Amplitude Modulation)، موج مدولهشده (Modulated wave) از موج حامل و دو باند جانبی (Sidebands) تشکیل شده است. اطلاعات موج مدوله شده فقط در باندهای جانبی آن قرار گرفته است. در واقع باند جانبی، یک باند از فرکانسهای مختلف است که حاوی توان هستند. به عبارت دیگر، باندهای جانبی فرکانسهای بالا و پایین مربوط به فرکانس سیگنال حامل را نشان میدهند. به انتقال یک سیگنال که موج حامل دارای دو باند جانبی است، مدولاسیون حامل کامل باند جانبی مضاعف (Double Sideband Full Carrier) یا به اختصار DSBFC میگویند. در تصویر زیر، نمایی از سیگنال در مدولاسیون حامل کامل باند جانبی مضاعف یا DSBFC نشان داده شده است.

البته باید به این نکته توجه شود که این انتقال اطلاعات با کمک روش مدولاسیون DSBFC دو مشکل بزرگ دارد. اولا این مدولاسیون یک روش غیر بهینه و ناموثر محسوب میشود؛ زیرا حدود دو سوم از توان سیستم، در سیگنال حامل تلف میشود. این امر در حالی اتفاق میافتد که سیگنال حامل هیچ اطلاعات مفیدی را در خود ندارد. دوما پهنای باند این روش دو برابر پهنای باند سیگنال پیام است.
اگر بتوان سیگنال حامل را به طریقی سرکوب یا حذف (Suppressed) کرد، آنگاه مقدار توانی که از این کار ذخیره میشود، در دو باند جانبی توزیع میشود. در این حالت به فرایند، یک مدولاسیون حامل سرکوب شده باند جانبی مضاعف (Double Sideband Suppressed Carrier) یا به اختصار DSBSC میگویند. انتقال اطلاعات با روش مدولاسیون حامل حذف شده، باعث میشود یکی از دو مشکل بزرگ که در روش مدولاسیون حامل کامل باند جانبی مضاعف با آن رو به رو بودیم، حل شود. نمایی از سیگنال مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC در تصویر زیر نشان داده شده است.
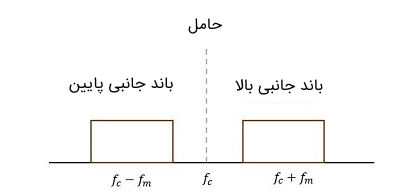
همان طور که در تصویر فوق مشاهده میشود، سیگنال حامل سرکوب شده است و باندهای جانبی مجاز به انتقال هستند.
بیان ریاضی مدولاسیون DSBSC
همانند روشهای مدولاسیون دیگر، در این قسمت نیز فرمولهای ریاضی مخصوص برای سیگنالهای حامل و پیام را تعریف میکنیم. عبارت ریاضی مربوط به سیگنال پیام یا مدولهکننده به صورت زیر نوشته میشود:
$$ m \left ( t \right ) = A _ m \cos \left ( 2 \pi f _ m t \right ) $$
همچنین سیگنال حامل را میتوان به صورت زیر نوشت:
$$ c \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) $$
به لحاظ ریاضی، معادله شکل موج سیگنال مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا مدولاسیون DSBSC را میتوان به صورت حاصل ضرب بین دو سیگنال پیام و سیگنال حامل و مطابق با رابطه زیر بیان کرد:
$$ s \left ( t \right ) = m \left ( t \right ) c \left ( t \right ) $$
$$ \Rightarrow s \left ( t \right ) = A _ m A _ c \cos \left ( 2 \pi f _ m t \right ) \cos \left ( 2 \pi f _ c t \right ) $$
پهنای باند سیگنال مدولاسیون DSBSC
از قبل میدانیم که برای محاسبه پهنای باند (Bandwidth) یا BW یک سیگنال باید فرکانس پایین سیگنال را از فرکانس بالای آن کم کنیم.
در نتیجه داریم:
$$ B W = f _ { m a x } - f _ { m i n } $$
حال معادله ریاضی مربوط به سیگنال مدولاسیون DSBSC، که در قسمت قبل به دست آوردیم را در نظر میگیریم:
$$ \Rightarrow s \left ( t \right ) = A _ m A _ c \cos \left ( 2 \pi f _ m t \right ) \cos \left ( 2 \pi f _ c t \right ) $$
این معادله را میتوان به صورت زیر نیز نوشت:
$$ \Rightarrow s \left ( t \right ) = \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c + f _ m \right ) t \right ] + \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c - f _ m \right ) t \right ] $$
سیگنال مدوله شده توسط روش مدولاسیون حامل سرکوب شده باند جانبی مضاعف، فقط شامل دو فرکانس است. بنابراین فرکانسهای کمینه و بیشینه را میتوان به ترتیب به صورت $$ f _ c - f _ m $$ و $$ f _ c + f _ m $$ نوشت:
$$ f _ { m a x } = f _ c + f _ m $$
$$ f _ { m i n } = f _ c - f _ m $$
حال میخواهیم مقادیر $$ f _ { m a x } $$ و $$ f _ { m i n } $$ را در رابطه ریاضی محاسبه پهنای باند جایگزین کنیم.
$$ BW = f _ c + f _ m - \left ( f _ c - f _ m \right ) $$
$$ \Rightarrow BW = 2 f _ m $$
بر اساس رابطه به دست آمده در بالا، میتوان گفت که پهنای باند موج مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC مشابه با پهنای باند موج مدولاسیون دامنه یا AM است و دقیقا دو برابر فرکانس سیگنال پیام محاسبه میشود. در نتیجه انتقال اطلاعات با روش مدولاسیون حامل حذف شده باند جانبی مضاعف، از نظر مشکل پهنای باند کاملا مشابه با روش مدولاسیون حامل کامل عمل میکند و پهنای باند دو برابر پهنای باند سیگنال پیام را اشغال میکند.
محاسبات توان موج مدولاسیون DSBSC
معادله زیر را در نظر بگیرید که مربوط به سیگنال مدوله شده حامل سرکوب شده باند جانبی مضاعف است:
$$ s \left ( t \right ) = \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c + f _ m \right ) t \right ] + \frac { A _ m A _ c } { 2 } \cos \left [ 2 \pi \left ( f _ c - f _ m \right ) t \right ] $$
توان سیگنال مدولاسیون DSBSC برابر با مجموع توان مولفههای فرکانسی باند جانبی بالا و باند جانبی پایین است و به صورت رابطه زیر نوشته میشود:
$$ P _ t = P _ { U S B } + P _ { L S B } $$
همچنین میدانیم که فرمول استاندارد برای محاسبه توان سیگنال کسینوسی به صورت زیر به دست میآید:
$$ P = \frac { { v _ { r m s } } ^ { 2 } } { R } = \frac { \left ( v _ m \sqrt { 2 } \right ) ^ 2 } { R } $$
ابتدا میخواهیم توان مربوط به باند جانبی بالا سیگنال مدولاسیون DSBSC را به دست آوریم.
این مقدار به صورت زیر محاسبه میشود:
$$ P _ { U S B } = \frac { \left ( A _ m A _ c / 2 \sqrt { 2 } \right ) ^ 2 } { R } = \frac { { A _ { m } } ^ { 2 } { A _ { c } } ^ { 2 } } { 8 R } $$
حال به طریق مشابه، توان مربوط به باند جانبی پایین را میتوان به دست آورد:
$$ P _ { U S B } = \frac { { A _ { m } } ^ { 2 } { A _ { c } } ^ { 2 } } { 8 R } $$
برای به دست آوردن توان کلی مربوط به سیگنال مدولاسیون DSBSC، باید توان باند جانبی بالا و توان باند جانبی پایین را با یکدیگر جمع کرد:
$$ P _ t = \frac { { A _ { m } } ^ { 2 } { A _ { c } } ^ { 2} } { 8 R } + \frac { { A _ { m } } ^ { 2 } { A _ { c } } ^ { 2 } } { 8 R } $$
$$ \Rightarrow P _ t = \frac { { A _ { m } } ^ { 2 } { A _ { c } } ^ { 2 } } { 4 R } $$
اگر این مطلب برای شما مفید بوده است، مطالب و آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۱
- اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
- اشمیت تریگر با اپ امپ — از صفر تا صد
- نسبت سیگنال به نویز چیست؟ — از صفر تا صد
^^










