حلقه قفل فاز (PLL) چیست؟ – از صفر تا صد

حلقه قفل فاز (Phase-Locked Loop) یا به اختصار PLL یک سیستم کنترلی است که کاربردهای فراوانی در الکترونیک و مخابرات دارد. در واقع، حلقه قفل فاز می‌تواند یک سیگنال خروجی را تولید کند که فاز آن به فاز سیگنال ورودی وابسته است. حلقه قفل فاز انواع مختلفی دارد، اما ساده‌ترین نوع آن، یک مدار الکترونیکی است که از یک اسیلاتور فرکانس متغیر (Variable Frequency Oscillator) و یک آشکارساز فاز (Phase Detector) در حلقه فیدبک تشکیل شده است. اسیلاتور در این مدار، یک سیگنال متناوب تولید می‌کند و آشکارساز فاز، مسئول مقایسه فاز آن سیگنال با فاز سیگنال متناوب ورودی است و در نهایت، باید اسیلاتور برای حفظ تطبیق فاز تنظیم شود. در این مطلب قصد داریم به معرفی حلقه قفل فاز بپردازیم و اجزای تشکیل‌دهنده و تابع انتقال یک مدار حلقه قفل فاز را مورد بررسی قرار دهیم و در نهایت، یک آی‌سی حلقه قفل فاز را معرفی کنیم.

می‌توان گفت حفظ فاز یکسان برای سیگنال ورودی و خروجی، روی حفظ فرکانس یکسان برای سیگنال ورودی و خروجی نیز تاثیر می‌گذارد. در نتیجه، علاوه بر سنکرون کردن سیگنال‌های ورودی و خروجی، یک حلقه قفل فاز می‌تواند فرکانس سیگنال ورودی را نیز تعقیب کند و یا یک فرکانس خروجی ایجاد کند که مضربی از فرکانس ورودی باشد. این مشخصه در بسیاری از کاربردها مانند سنکرون‌سازی کلاک کامپیوترها، دمدولاتورها و ترکیب فرکانسی به شدت مورد نیاز است.

حلقه قفل فاز در رادیو، مخابرات، کامپیوترها و سایر کاربردهای الکترونیکی مورد استفاده قرار می‌گیرد. از این مدارات می‌توان برای دمدولاسیون یک سیگنال، بازیابی یک سیگنال از یک کانال مخابراتی نویزی، تولید یک فرکانس پایدار در ترکیب‌کننده‌های فرکانسی و یا توزیع دقیق پالس‌های کلاک در ادوات الکترونیکی مدرن با فرکانس‌های خروجی کسری از هرتز تا چندین گیگا هرتز استفاده کرد.

اساس حلقه قفل فاز

حلقه قفل فاز یا PLL، اساسا دارای فرم حلقه سرو (Servo Loop) است. در واقع می‌توان گفت که حلقه قفل فاز عملیات خود را روی سیگنال فرکانس رادیویی انجام می‌دهد، اما تمام معیارهای اساسی در مورد پایداری حلقه و سایر پارامترها، کاملا با سایر انواع حلقه فیدبک یکسان هستند. به همین دلیل، تمام تئوری‌هایی که به حلقه سرو (Servo Loop) اعمال می‌شوند را می‌توان به حلقه قفل فاز نیز اعمال کرد.

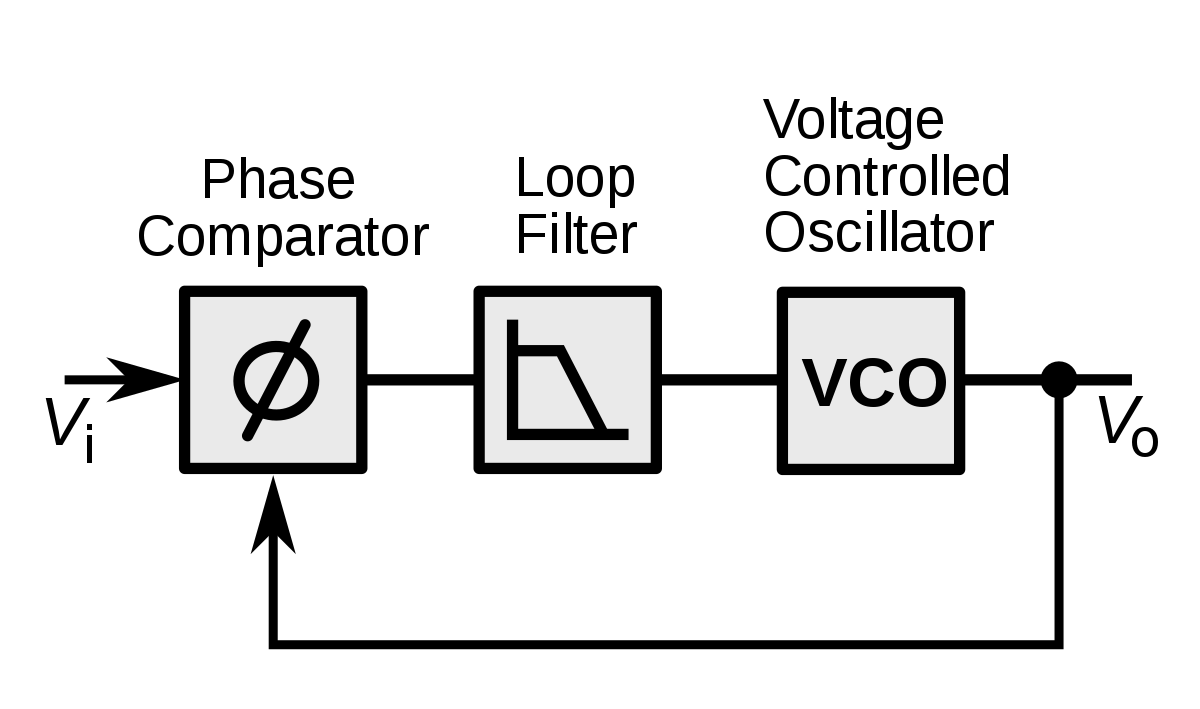
در تصویر زیر، یک دیاگرام ساده از حلقه قفل فاز را می‌توان مشاهده کرد.

بر اساس بلوک دیاگرام فوق، حلقه قفل فاز از سه المان اساسی تشکیل شده است.

آشکارساز فاز (Phase Detector)

همان طور که از نام این مدار مشخص است، وظیفه اصلی آن در حلقه قفل فاز، مقایسه فاز دو سیگنال است تا بر اساس اختلاف فاز بین آن‌ها، یک ولتاژ اختلافی در مدار ایجاد شود. این مدار انواع مختلفی دارد. برخی آشکارسازهای فاز از ادوات منطقی مانند گیت XOR و یا فلیپ فلاپ JK بهره می‌برند، در حالی که در برخی دیگر از آن‌ها، یک مدار حلقه دیودی برای تشخیص اختلاف فاز مورد استفاده قرار می‌گیرد. برای آشنایی بیشتر با مدارات آشکارساز فاز در حلقه قفل فاز می‌توانید به مطلب آشکارساز فاز در مجله فرادرس مراجعه کنید.

اسیلاتور کنترل شده با ولتاژ (Voltage Controlled Oscillator) یا VCO

اسیلاتور کنترل شده با ولتاژ مداری است که وظیفه ایجاد سیگنال فرکانس رادیویی (Radio Frequency Signal) را بر عهده دارد. این سیگنال معمولا به صورت خروجی حلقه در نظر گرفته می‌شود. فرکانس مدار VCO می‌تواند در طول باند فرکانسی عملیاتی مورد نیاز حلقه کنترل شود.

فیلتر حلقه (Loop Filter)

این مدار به منظور فیلتر کردن خروجی مقایسه‌گر یا آشکارساز فاز در حلقه قفل فاز مورد استفاده قرار می‌گیرد. این فیلتر هر مولفه‌ای از سیگنال‌های مقایسه شده در آشکارساز فاز را از خط VCO یا به عبارت دیگر ورودی VCO و سیگنال مرجع حذف می‌کند. این مدار همچنین بسیاری از مشخصه‌های حلقه مانند پایداری حلقه، سرعت قفل و ... را تعیین می‌کند.

در عملکرد کلی حلقه قفل فاز، طراحی فیلتر حلقه از اهمیت بسیار بالایی برخوردار است. مدار واقعی فیلتر حلقه در حلقه قفل فاز، ساختار بسیار ساده‌ای دارد، اما تاثیر آن روی عملکرد حلقه قفل فاز بسیار گسترده است. در طراحی مدار فیلتر حلقه، انتخاب مقادیر معمولا به نحوی انجام می‌گیرد که یک تعادل بسیار دقیق بین تعدادی الزامات متناقض (Conflicting Requirements) به دست آید.

تاثیرات فیلتر حلقه روی عملکرد حلقه قفل فاز

مشخصه‌های فیلتر حلقه روی برخی از کارکردهای حلقه قفل فاز تاثیر می‌گذارد. مهم‌ترین این مشخصه‌ها عبارتند از:

فرکانس مقایسه فیلتر (Filter Comparison Frequency): یکی از مهم‌ترین کارکردهای فیلتر حلقه، حذف مولفه‌های ناخواسته از فرکانس‌های آشکارساز فاز یا مقایسه کننده فاز است. اگر این فرکانس‌ها در ورودی مدار اسیلاتور کنترل شده با ولتاژ یا VCO ظاهر شوند، آن‌گاه در باندهای جانبی (Side Bands)، آفست‌هایی از سیگنال حامل با فرکانسی برابر با فرکانس آشکارساز فاز ظاهر می‌شود.

پایداری حلقه: نقاط قطع و Roll Off (به نقطه‌ای می‌گوییم که شیب پاسخ فرکانسی فیلتر غیرصفر و منفی می‌شود.) در فیلتر حلقه از اهمیت بالایی برخوردار هستند. فیلتر باید به صورتی طراحی شود که در نقاط بهره واحد از حلقه کلی، به بهره حلقه نزول یابد، در غیر این صورت، حلقه ناپایدار خواهد شد.

پاسخ گذرا (Transient Response): در برخی کاربردها ممکن است ضروری باشد که حلقه قفل فاز سیگنال دیگری را تعقیب کند یا فرکانس خود را تغییر دهد. فیلتر حلقه، به گونه‌ای عمل می‌کند که سرعت پاسخ کاهش یابد. هر چقدر پهنای باند فیلتر باریک‌تر باشد، فرکانس قطع فیلتر پایین‌تر خواهد بود و در نتیجه، سرعت پاسخ حلقه برای پاسخ دادن به تغییرات پایین‌تر خواهد بود و برعکس، اگر حلقه به یک پاسخ سریع به تغییرات در فرکانس نیاز داشته باشد، آن‌گاه به پهنای باند حلقه وسیع‌تر نیاز است.

عملکرد حلقه قفل فاز

مفاهیم اساسی در عملکرد حلقه قفل فاز، ساده هستند، اما محاسبات ریاضی و المان‌های زیاد در عملکرد مدار آن بسیار پیچیده به نظر می‌رسند. بلوک دیاگرام یک سیستم حلقه قفل فاز، نشان دهنده سه المان اساسی در عملکرد هستند. این المان‌ها، همان طور که در بخش قبل به صورت اختصاری معرفی شدند، عبارتند از: آشکارساز فاز، اسیلاتور کنترل شده با ولتاژ و فیلتر حلقه.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

در یک مدار حلقه قفل فاز ساده، سیگنال مرجع و سیگنال اسیلاتور کنترل شده با ولتاژ، به دو پورت ورودی مدار آشکارساز فاز متصل می‌شوند. خروجی مدار آشکارساز فاز، که یک سیگنال خطا است، به فیلتر حلقه وارد می‌شود و سپس ولتاژ خطای فیلتر شده، به اسیلاتور کنترل شده با ولتاژ باز گردانده می‌شود. دیاگرام عملکرد حلقه قفل فاز در تصویر زیر نشان داده شده است.

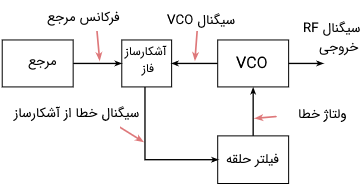
اسیلاتور کنترل شده با ولتاژ یا VCO در حلقه قفل فاز، سیگنالی را تولید می‌کند که وارد آشکارساز فاز می‌شود. در اینجا فاز سیگنال‌های تولیدی در اسیلاتور کنترل شده با ولتاژ و سیگنال مرجع ورودی با یکدیگر مقایسه می‌شوند و یک سیگنال خطا به عنوان نتیجه حاصل می‌شود. این مقدار خطا، متناظر با مقدار اختلاف فاز بین دو سیگنال است.

سیگنال خطا ایجاد شده توسط آشکارساز فاز، از یک فیلتر پایین گذر عبور می‌کند که بسیاری از مشخصه‌های حلقه کلی را تعیین می‌کند. فیلتر پایین گذر، هر المان فرکانس بالا در سیگنال خطا را حذف می‌کند. سیگنال خطا پس از عبور از فیلتر، به عنوان ولتاژ تنظیم‌کننده، به ترمینال کنترل اسیلاتور کنترل شده با ولتاژ اعمال می‌شود. اندازه‌گیری میزان تغییرات در ولتاژ خطا، با این هدف انجام می‌گیرد که مدار تلاش کند تا اختلاف فاز و در نتیجه اختلاف فرکانس بین دو سیگنال را کاهش دهد.

در ابتدا حلقه در حالت قفل نیست، اما ولتاژ خطای به وجود آمده، فرکانس اسیلاتور کنترل شده با ولتاژ را به سمت فرکانس سیگنال مرجع سوق می‌دهد و این کار تا زمانی ادامه می‌یابد که مدار نتواند خطا را بیشتر از آن کاهش دهد و در نتیجه مدار در این حالت قفل خواهد شد. زمانی که حلقه قفل فاز، در مود قفل قرار گیرد، یک خطای ولتاژ حالت ماندگار به وجود می‌آید. با استفاده از یک تقویت‌کننده بین آشکارساز فاز و مدار اسیلاتور، خطای واقعی بین سیگنال‌ها را می‌توان به سطح بسیار کوچکی کاهش داد. با این حال، باید همیشه مقداری ولتاژ در ترمینال مدار اسیلاتور VCO وجود داشته باشد؛ زیرا این ولتاژ مدار را به سمت فرکانس صحیح هدایت می‌کند.

این واقعیت که ولتاژ خطای پایدار در مدار وجود دارد، به این معنی است که فاز بین سیگنال مرجع و سیگنال VCO تغییر نمی‌کند. عدم تغییر فاز بین این دو سیگنال باعث می‌شود که دو سیگنال دقیقا دارای فرکانس یکسانی باشند.

تابع انتقال حلقه قفل فاز

در تصویر زیر یک دیاگرام دیگر از حلقه قفل فاز را می‌توان مشاهده کرد.

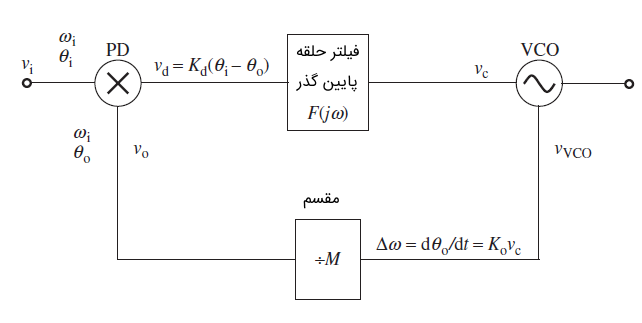
زمانی که دو ورودی، سیگنال‌هایی کوچک باشند، آشکارساز فاز در این مدار یک ضرب‌کننده خواهد بود.

دو سیگنال ورودی را به صورت زیر فرض می‌کنیم:

$$\begin {aligned} &v_{ \mathrm { i }} ( t) = V_{ \mathrm { s }} \sin \left( \omega_{ \mathrm { i }} t + \theta_{ \mathrm { i }} \right)\\ &v_{ \mathrm { o }} ( t ) = V_{ \mathrm { o }} \cos \left( \omega_{ \mathrm{ i }} t + \theta_{ \mathrm { o }} \right) \end{aligned}$$

در روابط فوق، $$v_i$$ سیگنال ورودی به آشکارساز فاز، $$v_o$$ ورودی دوم آشکارساز فاز از مدار مقسم، $$\omega _i$$ فرکانس سیگنال ورودی، $$\theta _i$$ فاز سیگنال ورودی و $$\theta _o$$ فاز سیگنال خروجی از مقسم هستند.

معادله اساسی حلقه در دیاگرام فوق به صورت زیر به دست می‌آید:

$$v_{ \mathrm { d } } ( t ) = K_{\mathrm{m}} v_{ \mathrm { i }} ( t ) \cdot v_{ \mathrm { o }} ( t ) = \frac {1} { 2} K_{ \mathrm { m }} V_{ \mathrm { s }} V_{ \mathrm { o }} \sin \left (2 \omega_{ \mathrm{ i }} t + \theta_{ \mathrm{ i }} + \theta_{ \mathrm { o }} \right) + \frac{ 1 } { 2} K_{ \mathrm { m }} V_{ \mathrm { s }} V_{ \mathrm { o }} \sin \left( \theta_{ \mathrm { i }} - \theta_{ \mathrm { o }} \right)$$

که در این رابطه، $$K_m$$ برابر با فاکتور ضرب در ضرب‌کننده با ابعاد $$[V^ {-1}]$$ است.

به دلیل وجود فیلتر پایین گذر در حلقه، می‌توان از فرکانس‌های بالا در روابط صرف نظر کرد و رابطه را به صورت زیر بازنویسی کرد.

$${v_{ \mathrm { d }} ( t ) \approx K_{ \mathrm { m }} v_{ \mathrm { i }} ( t) \cdot v_{ \mathrm { o }} ( t ) = \frac {1 } {2} K_{ \mathrm { m }} V_{ \mathrm { s }} V_{ \mathrm { o }} \sin \left( \theta_{ \mathrm { i }} - \theta_{ \mathrm { o }} \right) = K_{ \mathrm { d }} \sin \left( \theta_{ \mathrm { i }}- \theta_{ \mathrm { o }}\right)}$$

در رابطه جدید، $$K_{\mathrm{d}}=\frac{1}{2} K_{\mathrm{m}} V_{\mathrm{s}} V_{\mathrm{o}}$$ برابر با فاکتور بهره ضرب‌کننده در آشکارساز فاز است و با واحد ولت بر رادیان اندازه‌گیری می‌شود. خروجی فیلتر حلقه میان گذر برابر است با:

$$v_{ \mathrm { c }}( t ) = v_{ \mathrm { d }}( t ) F ( j \omega)$$

تغییرات فاز در خروجی مدار اسیلاتور کنترل شده با ولتاژ به صورت خطی با ولتاژ کنترل در ورودی VCO متناسب است. بنابراین می‌توان نوشت:

$$M \frac { \mathrm { d } \theta_{ \mathrm { o }}} { \mathrm { d } t} = K_{ \mathrm { o }} v_{ \mathrm { c}}$$

که در این فرمول، $$K_0$$ برابر با فاکتور بهره اسیلاتور کنترل شده با ولتاژ و $$M$$ مرتبه تقسیم مقسم است. با استفاده از نوتیشن لاپلاس، معادلات اساسی حلقه را می‌توان به صورت زیر بازنویسی کرد:

$$v_{ \mathrm { d }} ( s ) = K_{ \mathrm { d }} \left [ \theta_{ \mathrm { i }}( s ) - \theta_{ \mathrm { o }} ( s ) \right]$$

$$v_{\mathrm{c}}(s)=v_{\mathrm{d}}(s) F(s)$$

$$\theta_{ \mathrm { o }} = \frac {K_{ \mathrm { o }} v_{ \mathrm { c }} ( s )}{ s M}$$

تابع تبدیل حلقه باز یا بهره حلقه باز به صورت زیر محاسبه می‌شود:

$$G(s) = \frac { \theta_{ \mathrm { o }} ( s )} { \theta_{ \mathrm { e }} ( s )} = \frac { \theta_{ \mathrm { o }} ( s )} { \theta_{ \mathrm { i }} ( s ) - \theta_{ \mathrm { o }}(s)}=\frac{K_{\mathrm{o}} K_{\mathrm{d}} F(s)}{s M}$$

اختلاف فاز بین دو سیگنال ورودی به آشکارساز فاز را با $$\theta _e$$ نشان می‌دهیم و به صورت زیر آن را محاسبه می‌کنیم:

$$\theta_{ \mathrm {e }} ( s ) = \theta_{ \mathrm { i }} ( s) - \theta_{ \mathrm { o }} ( s)$$

تابع انتقال حلقه بسته حلقه قفل فاز به صورت زیر به دست می‌آید:

$$H( s ) = \frac {\theta_{ \mathrm { o }} ( s )} { \theta_{ \mathrm { i }} ( s )} = \frac {K_{ \mathrm { o }} K_{ \mathrm { d } } F( s )} { s M + K_{ \mathrm { o }} K_{ \mathrm { d }} F(s )} = \frac { G( s )} { 1 + G( s)}$$

$$1-H(s) = \frac { \theta_{ \mathrm {e}} ( s)}{\theta_{\mathrm{i}}(s)} = \frac{\theta_{\mathrm{i}}(s)-\theta_{\mathrm{o}}(s)}{\theta_{\mathrm{i}}(s)}=\frac{s M}{s M+K_{\mathrm{o}} K_{\mathrm{d}} F(s)}$$

ولتاژ ورودی به اسیلاتور کنترل شده با ولتاژ را می‌توان به طریق زیر به دست آورد:

$$v_{ \mathrm { c }} ( s ) = v_{ \mathrm { d }} ( s ) F( s ) = K_{ \mathrm { d }} \theta_{ \mathrm { e }} (s ) F(s) \\ =\frac{s M K_{\mathrm{d}} F(s) \theta_{\mathrm{i}}(s)}{s M+K_{\mathrm{o}} K_{\mathrm{d}} F(s)}=\frac{s M \theta_{\mathrm{i}}(s)}{K_{\mathrm{o}}} H(s)$$

در حلقه قفل فاز معمولا فیلتر حلقه پایین گذر، یک فیلتر پسیو یا یک فیلتر اکتیو مرتبه دوم است. در تصویر زیر می‌توان شماتیک این دو فیلتر را مشاهده کرد.

تابع انتقال یک فیلتر پسیو که در شکل سمت چپ نشان داده شده است را می‌توان به صورت زیر نوشت:

$$F_{ \mathrm { psv }} ( s ) = \frac {s C_{ \mathrm { p }} R_{2 \mathrm { p }} + 1 }{ s C_{ \mathrm { p }} \left (R_{1 \mathrm { p }} + R_{2 \mathrm { p }} \right ) + 1} = \frac {s \tau_{2 \mathrm { p }} + 1} { s \tau_{ 1 \mathrm { p }} + 1 }$$

که در آن داریم:

$$\tau_{1 \mathrm { p }} = C_{ \mathrm { p }} \left(R_{ 1 \mathrm { p }} + R_{2 \mathrm { p }} \right)$$

$$\tau_{2 \mathrm { p }} = C_{ \mathrm { p }} R_{2 \mathrm { p}}$$

تابع انتقال مربوط به یک فیلتر اکتیو که در شکل سمت راست تصویر فوق دیده می‌شود را نیز می‌توان به صورت زیر نوشت:

$$F_{ \mathrm { atv }} ( s ) = \frac {-A \left ( s C_{ \mathrm { a }} R_{2 \mathrm { a }} + 1 \right )} { s C_{ \mathrm { a }} R_{2 \mathrm { a }} + 1 + (1 + A ) s C_{\mathrm { a }} R_{ \mathrm {la}}}$$

اگر $$A \gg 1$$ باشد، آن‌گاه داریم:

$$F_{ \mathrm { atv }} ( s ) = \frac {s C_{ \mathrm { a }} R_{2 \mathrm { a }} + 1 }{S C_{ \mathrm { a }} R_{1 \mathrm { a }}} = \frac {s \tau_{2 \mathrm { a }} + 1 } { s \tau_{ \mathrm{la }}}$$

در رابطه فوق موارد زیر برقرار هستند:

$$\tau_{1 \mathrm { a }} = C_{ \mathrm { a }} R_{1 \mathrm{a}}$$

$${\tau_{2 \mathrm { a }} = C_{ \mathrm{ a }} R_{2 \mathrm{a}}}$$

تابع انتقال حلقه بسته فیلتر پسیو و اکتیو مرتبه دوم به صورت زیر به دست می‌آید. برای فیلتر پسیو می‌توان نوشت:

$$H_{ \mathrm { psv }} ( s)=\frac{K_{\mathrm { o }} K_{\mathrm { d} } \left ( s \tau_{2 \mathrm { p }} + 1 \right) / \tau_{1 \mathrm { p }}} { s^{ 2 }+ s \left ( 1 + K_{ \mathrm { o }} K_{\mathrm{d}} \tau_{2 \mathrm{p}}\right) / \tau_{1 \mathrm{p}}+K_{\mathrm{o}} K_{\mathrm{d}} / \tau_{\mathrm{lp}}}$$

و برای فیلتر اکتیو مرتبه دوم نیز داریم:

$$ H_{ \mathrm { atv }} (s) = \frac {K_{ \mathrm { o }} K_{\mathrm{d}} \left ( s \tau_{ 2 \mathrm { a }}+ 1 \right) / \tau_{ \mathrm { la }}} { s^{2} + s \left ( K_{ \mathrm { o }} K_{ \mathrm { d }} \tau_{2 \mathrm { a }} /  \tau_{ 1 \mathrm { a }} \right) + K_{\mathrm{o}} K_{\mathrm{d}} / \tau_{\mathrm{la}}}<br /> \ $$

این دو تابع انتقال حلقه بسته را می‌توان به این صورت بازنویسی کرد:

$$H_{\mathrm { psv }}( s ) = \frac {s \left(2 \zeta_{ \mathrm { p }} \omega_{\mathrm{ np }} - \omega_{\mathrm{ np }}^{2} / K_{\mathrm{ o }} K_{\mathrm{d}}\right)+\omega_{ \mathrm{np}}^{ 2 }}{ s ^{2}+2 \zeta_{\mathrm { p }} \omega_{\mathrm{ np }} s + \omega_{ \mathrm{ np }}^{2}}$$

که در آن $$\omega _{ np }$$ برابر با فرکانس طبیعی حلقه و $$\zeta _p$$ برابر با فاکتور میرایی هستند. در نتیجه می‌توان روابط زیر را برای فیلتر پسیو نوشت:

$$\omega_{ \mathrm { np }} = \sqrt {\frac {K_{\mathrm{o}} K_{ \mathrm {d}}}{ \tau_{\mathrm{lp}}}}$$

$$\zeta_{\mathrm{p}}=\frac{1}{2} \sqrt{\frac{K_{\mathrm{o}} K_{\mathrm{d}}}{\tau_{\mathrm{lp}}}}\left(\tau_{2 \mathrm{p}}+\frac{1}{K_{\mathrm{o}} K_{\mathrm{d}}}\right)$$

همچنین برای فیلتر اکتیو مرتبه دوم روابط زیر برقرار هستند:

$$H_{ \mathrm{atv}} (s) = \frac {2 \zeta_{ \mathrm{ a } } \omega_{\mathrm { na }} s + \omega_{ \mathrm { na }}^{ 2 }} {s^{2 } + 2 \zeta_{\mathrm { a }} \omega_{ \mathrm {na}} s + \omega_{\mathrm{na}}^{2}}$$

$$\omega_{\mathrm{na}} = \sqrt { \frac {K_{ \mathrm{ o }} K_{ \mathrm { d }}}{ \tau_{ \mathrm {la}}}}$$

$$\zeta_{ \mathrm { a }} = \frac { \tau_{2 \mathrm {a}}} {2} \sqrt { \frac {K_{\mathrm{o}} K_{\mathrm { d }}}{ \tau_{\mathrm{ la }}}} = \frac { \tau_{2 \mathrm{ a }}} {2} \omega_{ \mathrm {na}}$$

آی‌سی حلقه قفل فاز ۵۶۵

عملکرد حلقه قفل فاز در یکی از سه مود زیر قرار دارد:

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

• مود آزادگرد (Free Running Mode)
• مود تسخیر (Capture Mode)
• مود قفل (Lock Mode)

در ابتدا، زمانی که هیچ ورودی اعمال نشده باشد، عملکرد حلقه قفل فاز در حالت آزادگرد قرار دارد. زمانی که یک سیگنال با یک فرکانس خاص به مدار اعمال شود، فرکانس سیگنال خروجی از اسیلاتور کنترل شده با ولتاژ، شروع به تغییر می‌کند. در این مرحله، گفته می‌شود که حلقه قفل فاز در مود تسخیر قرار می‌گیرد. فرکانس سیگنال خروجی از اسیلاتور کنترل شده با ولتاژ به صورت پیوسته تغییر می‌کند تا زمانی که فرکانس آن با فرکانس سیگنال ورودی برابر شود. زمانی که مدار به این هدف برسد و دو فرکانس با یکدیگر برابر شوند، مدار در مود قفل قرار می‌گیرد.

یکی از متداول‌ترین آی‌سی‌هایی که به عنوان مدار حلقه قفل فاز مورد استفاده قرار می‌گیرد، آی‌سی ۵۶۵ است. این آی سی یک پکیج ۱۴ پینی دو ردیفه یا DIP است که دیاگرام پین‌های آی‌سی ۵۶۵ را می‌توان در تصویر زیر مشاهده کرد.

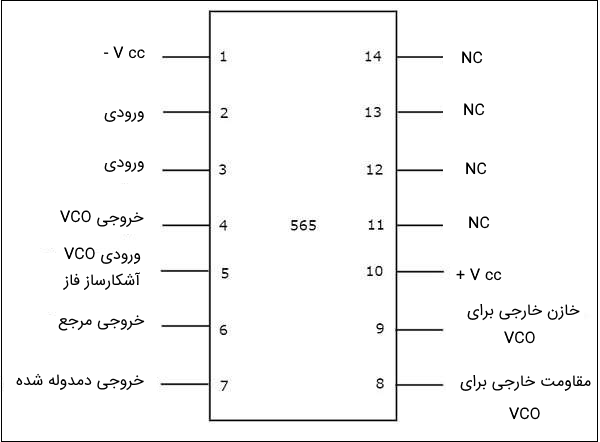
می‌توان با مراجعه به تصویر فوق به کاربرد هر پین پی برد. برای عملکرد آی سی به عنوان حلقه قفل فاز، لازم است که فقط از ۱۰ پایه از ۱۴ پایه آن استفاده کنیم. این پایه‌ها از شماره ۱ تا ۱۰ در تصویر فوق مشخص شده‌اند. اما ۴ پایه باقی مانده یعنی پایه‌های ۱۱ تا ۱۴ با علامت NC مشخص شده‌اند که به معنای عدم اتصال (No Connection) است.

خروجی مدار VCO، که در واقع خروجی کل حلقه قفل فاز نیز محسوب می‌شود، در پین شماره ۴ از آی سی ۵۶۵ قرار دارد. در این مدار پین‌های شماره ۲ و ۳ به زمین متصل شده‌اند. فرکانس خروجی مدار اسیلاتور کنترل شده با ولتاژ $$f_{out}$$ را می‌توان به صورت ریاضی مطابق با رابطه زیر نشان داد.

$$f_{out} = \frac {0.25} {R_V C_V}$$

در رابطه بالا، $$R_V$$، مقاومت خارجی متصل به پین شماره ۸ آی‌سی و $$C_V$$، خازن خارجی متصل به پین شماره ۹ آی‌سی است. با انتخاب مقادیر مناسب برای $$R_V$$ و $$C_V$$، می‌توان فرکانس خروجی مدار اسیلاتور کنترل شده با ولتاژ را تعیین کرد.

پین شماره ۴ و پین شماره ۵ باید توسط یک سیم خارجی به یکدیگر متصل شوند تا خروجی اسیلاتور کنترل شده با ولتاژ به عنوان یکی از ورودی‌ها به مدار آشکارساز فاز اعمال شود. آی سی ۵۶۵ دارای مقاومت داخلی ۳.6 کیلو اهم است و یک خازن C باید بین پین شماره ۷ و پین شماره ۱۰ متصل شود تا یک فیلتر پایین گذر را با مقاومت داخلی تشکیل دهد. حال آی‌سی آماده است تا به عنوان مدار حلقه قفل فاز مورد استفاده قرار گیرد.

کاربرد مدار حلقه قفل فاز

ورودی حلقه قفل فاز سیگنالی است که باید حلقه روی آن قفل شود. سپس مدار حلقه قفل فاز می‌تواند سیگنالی مشابه با سیگنال ورودی را در خروجی اسیلاتور کنترل شده با ولتاژ خود ایجاد کند. در نگاه اول ممکن است این کار مفید به نظر نرسد، اما با دقت بیشتر، می‌توان به کاربرد آن در بسیاری از مدارات پی برد. برخی از کاربردهای حلقه قفل فاز در زیر آورده شده‌اند.

دمدولاتور FM: یکی از مهم‌ترین کاربردهای حلقه قفل فاز در دمدولاتورهای FM است. به دلیل اینکه تولید آی‌سی‌های حلقه قفل فاز در حال حاضر بسیار ارزان است، کاربرد حلقه قفل فاز در دمدولاتورهای FM ما را قادر می‌سازد تا سیگنال‌های صوتی با کیفیت بالا را از یک سیگنال مدوله‌شده فرکانس یا FM دمدوله کنیم.

دمدولاتور AM: حلقه قفل فاز را می‌توان در دمدولاسیون سنکرون یک سیگنال مدوله‌شده دامنه یا AM مورد استفاده قرار داد. با استفاده از این روش، حلقه قفل فاز روی سیگنال حامل قفل می‌شود تا یک سیگنال مرجع در گیرنده تولید شود. چون فرکانس این سیگنال دقیقا با فرکانس سیگنال حامل متناظر است، در نتیجه می‌توان آن را با سیگنال ورودی ترکیب کرد و به صورت سنکرون دمدولاسیون دامنه را انجام داد.

ترکیب‌کننده‌های فرکانسی غیرمستقیم (Indirect Frequency Synthesizers): یکی از مهم‌ترین کاربردهای حلقه‌های قفل فاز، استفاده از آن‌ها در ترکیب‌کننده‌های فرکانسی است. اگرچه ترکیب‌کننده‌های دیجیتال مستقیم نیز می‌توانند مورد استفاده قرار بگیرند، اما ترکیب‌کننده‌های فرکانسی غیرمستقیم دارای کاربردهای خاص خود هستند و به همین دلیل یکی از مهم‌ترین کاربردهای حلقه قفل فاز را شکل می‌دهند.

بازیابی سیگنال (Signal Recovery): این قابلیت که حلقه قفل فاز می‌تواند روی یک سیگنال قفل کند، آن را قادر می‌سازد تا یک سیگنال صاف و اصطلاحا تمیز (Clean) را در خروجی ایجاد کند. حلقه قفل فاز می‌تواند در صورت ایجاد وقفه (Interruption) کوتاه، فرکانس سیگنال را به خاطر بسپارد. به همین دلیل، این حوزه از کاربردهای حلقه قفل فاز، در مداراتی مورد استفاده قرار می‌گیرد که امکان دارد برای یک بازه کوتاه زمانی در سیگنال وقفه ایجاد شود. به عنوان مثال، هنگام استفاده از انتقالات پالسی (Pulsed Transmissions) می‌توان از حلقه قفل فاز استفاده کرد.

در علم الکترونیک و مخابرات، شکل‌دهی پالس (Pulse Shaping) به فرایندی اطلاق می‌شود که طی آن، شکل موج پالس انتقال داده شده را تغییر می‌دهند. هدف از این کار این است که سیگنال انتقالی را برای هدف خود یا برای کانال مخابراتی منطبق‌تر کنند. معمولا این کار را با محدود کردن پهنای باند موثر انتقال انجام می‌دهند.

توزیع زمان (Timing Distribution): یکی دیگر از کاربردهای حلقه قفل فاز، توزیع بسیار دقیق پالس‌های کلاک زمان‌بندی در مدارت منطقی دیجیتال مانند یک سیستم میکروپروسسوری است.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی برق
• آموزش الکترونیک ۳
• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش طراحی فیلتر و سنتز مدار
• فیلتر میان گذر پسیو — از صفر تا صد
• اشمیت تریگر با اپ امپ — از صفر تا صد
• نسبت سیگنال به نویز چیست؟ — از صفر تا صد

^^