تجزیه اتحاد ها – آموزش گام به گام

در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، روش‌های تجزیه عبارت‌های جبری به کمک اتحادها آشنا می‌شویم. اتحادها چنان کاربرد فراوانی در تجزیه عبارت‌های جبری دارند، که گاهی دانش‌آموزان آن را به‌طور خلاصه تجزیه اتحاد ها می‌نامند. در این آموزش، ضمن معرفی اجمالی اتحادها، مثال‌های متنوعی را از کاربردشان در تجزیه بررسی خواهیم کرد.

عبارت جبری چیست؟

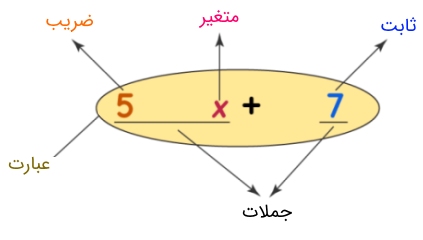
یک عبارت جبری (Algebraic Expression) ترکیبی از جملات با ثابت‌ها و متغیرها است که با عملیات جبری مانند جمع، تفریق، ضرب، تقسیم و غیره به هم پیوند داده شده‌اند. برای مثال، $$5x+7$$ یک عبارت جبری است. هر عبارت جبری اجزای مختلفی دارد که در تصویر زیر آن‌ها را نشان داده‌ایم.

تجزیه عبارت جبری چیست؟

وقتی می‌گوییم یک عبارت جبری را تجزیه کنیم، منظور این است که آن عبارت را که به‌‌صورت مجموع چند جمله بیان شده، به‌شکل حاصل‌ضرب چندجمله‌ای‌ها بنویسیم. برای مثال، عبارت جبری ساده $$2 x ^ 2 +2 x$$ را در نظر بگیرید. با فاکتور گرفتن از $$2 x$$، این عبارت ساده را می‌توان به‌صورت زیر نوشت:

$$\large 2 x ^ 2 + 2 x = 2 x (x + 1 )$$

می‌بینیم که یک عبارت جبری که به‌صورت مجموع جملات جبری بود، به‌شکل ضرب دو چندجمله‌ای نوشته شده است.

اما علاوه بر موارد ساده‌ای مانند فاکتورگیری، اتحادها نقش بسیار مهمی در تجزیه عبارت‌های جبری دارند. برای مثال، عبارت جبری $$x ^ 2 + 2 xy + y^2$$ با کمک اتحادها (در ادامه مهم‌ترینشان را معرفی می‌کنیم)‌ به‌صورت زیر تجزیه می‌شود:

$$\large x ^ 2 + 2 xy + y^2 = (x + y) ^ 2 =(x + y) (x + y )$$

در این آموزش، با تأکید بر کاربرد اتحادهای جبری، تجزیه اتحاد ها را با مثال‌های متنوعی بررسی می‌کنیم. در بخش بعدی، مهم‌ترین اتحادهای جبری معرفی می‌شوند.

مهم‌ترین اتحادهای جبری

اتحادها، در واقع، روابط و تساوی‌هایی هستند که به کمک آن‌ها می‌توان تجزیه عبارت‌ها را سریع‌تر و آسان‌تر انجام داد. برای مثال، دانستن اتحاد $$x ^ 2 + 2 xy + y^2 = (x + y) ^ 2$$ به ساده کردن و تجزیه عبارت‌های جبری کمک زیادی خواهد کرد.

در ادامه، با اتحادهای مهم آشنا می‌شویم که بهتر است آن‌ها را به خاطر بسپارید. در «تقلب نامه (Cheat Sheet) فرمول های جبری» می‌توانید به فایل PDF اتحادها دسترسی داشته باشید.

اتحاد مربع مجموع دوجمله ای (اتحاد اول)

اتحاد مربع مجموع دو جمله‌ای که به آن اتحاد اول نیز می‌گویند، در مواردی به‌کار می‌رود شکل عبارت بگونه‌ای باشد که بتوان آن را به‌صورت مجذور مجموع دو جمله نوشت.

$$\large (a+b)^ 2 = a ^ 2 + 2 ab+b^2$$

دقت کنید که $$a$$ و $$b$$ جمله هستند، یعنی می‌توانند عدد یا عبارت باشند. برای مثال، تساوی زیر را ببینید که در آن، $$a = xy$$ و $$b = 2 z$$:

$$\large (x y +2z)^ 2 = x ^ 2 y ^ 2 + 4 xyz+4 z ^ 2$$

اتحاد مربع تفاضل دوجمله ای (اتحاد دوم)

اتحاد مربع تفاضل دوجمله‌ای که به اتحاد دوم معروف است، مشابه اتحاد اول است و همان ویژگی‌ها را دارد، با این تفاوت که بین $$a$$ و $$b$$ علامت منفی قرار دارد. این اتحاد به‌صورت زیر است:

$$\large ( a - b )^ 2 = a ^ 2 - 2 a b + b ^ 2$$

اتحاد مربع سه جمله ای

اتحاد مربع جمع سه جمله به‌صورت زیر است:‌

$$\large (a+b+c)^2 = a ^ 2 +b^ 2 + c ^ 2 + 2 ab + 2ac +2bc$$

اتحاد مربع تفاضل سه جمله به‌شکل زیر است:‌

$$\large (a - b - c) ^ 2 = a ^ 2 + b ^ 2 + c ^ 2 - 2 ab - 2ac +2bc$$

اتحاد مکعب دوجمله ای

اتحاد مکعب دوجمله‌ای هنگامی مورد استفاده قرار می‌گیرد که توان سوم جملات در عبارت وجود داشته باشد و بتوان آن عبارت را به‌گونه‌ای نوشت که به یکی از دو فرم زیر (اولی برای مجموع دو جمله و دومی برای تفاضل دو جمله) بیان شود:

$$\large (a+b)^ 3 = a ^ 3 + 3a^2b+3ab^2+b^ 3$$

$$\large (a-b)^ 3 = a ^ 3 -3 a^2b+3ab^2-b^ 3$$

برای آشنایی بیشتر با این اتحاد، به آموزش «اتحاد مکعب دو جمله ای چیست ؟ — اثبات، فرمول و مثال — به زبان ساده» مراجعه کنید.

اتحاد مکعب سه جمله ای

اتحاد مکعب سه‌جمله‌ای به‌شکل زیر است:

$$\large \begin {align} &( a + b + c ) ^ { 3 } \\ & = 3 ( b + c ) ( a + b )( a + c )+ a ^ { 3 } + b ^ { 3 } + c ^ { 3 } \\ & = 3a^2b + 3a^2c + 3ab^2 + 3b^2c + 3ac^2 + 3bc^2 + 6abc \end {align}$$

برای آشنایی بیشتر با این اتحاد، آموزش «اتحاد مکعب چیست؟ — فرمول، اثبات و مثال — به زبان ساده» را مطالعه کنید.

اتحاد مزدوج

اتحاد مزدوج، یک از اتحادهای مهم و پرکاربرد است و در مواردی استفاده می‌شود که تفاضل مجذور دو جمله را داشته باشیم:

$$\large (a+b ) ( a - b ) = a ^ 2 - b ^ 2$$

برای آشنایی بیشتر با اتحاد مزدوج، به آموزش «اتحاد مزدوج چیست ؟ — فرمول، اثبات، مثال و حل تمرین» مراجعه کنید.

اتحاد جمله مشترک

$$\large ( x + a ) ( x + b ) = x ^ 2 + ( a + b ) x + a b$$

$$\large ( x + a ) ( x - b ) = x ^ 2 + ( a - b ) x - a b$$

برای آشنایی بیشتر با این اتحاد، پیشنهاد می‌کنیم به آموزش «اتحاد جمله مشترک چیست ؟ — فرمول، اثبات، مثال و حل تمرین» مراجعه کنید.

اتحاد چاق و لاغر

اتحاد چاق و لاغر یک تساوی است که مجموع یا تفاضل دو مکعب را تجزیه می‌کند.  اتحاد چاق و لاغر مجموع مکعبات به‌صورت زیر است:‌

$$\large a ^ 3 + b ^ 3 = ( a + b ) ( a ^ 2 - ab + b ^ 2 )$$

همچنین، این اتحاد برای تفاضل مکعبات به شکل زیر بیان می‌شود:‌

$$\large a ^ 3 - b ^ 3 = ( a - b ) ( a ^ 2 + ab + b ^ 2 )$$

در آموزش «اتحاد چاق و لاغر چیست ؟ — اثبات، فرمول، نمونه سئوال — به زبان ساده» مطالب کاملی درباره این اتحاد بیان کرده‌ایم.

چند اتحاد دیگر

اتحادهای دیگری نیز وجود دارند که شاید کمتر از اتحادهای معروف از آن‌ها استفاده شود، اما دانستن آن‌ها برای تجزیه اتحاد ها راهگشا خواهد بود. در ادامه، به مهم‌ترین ین اتحادها اشاره می‌کنیم.

$$\large \begin {aligned} ( a + b ) ^ { 4 } & = a ^ { 4 } + 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } + b ^ { 4 } \\ ( a - b ) ^ { 4 } & = a ^ { 4 } - 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } - 4 a b ^ { 3 } + b ^ { 4 } \\ a ^ { 4 } - b ^ { 4 } & = ( a - b ) ( a + b ) \left ( a ^ { 2 } + b ^ { 2 } \right ) \\ a ^ { 5 } - b ^ { 5 } & = ( a - b ) \left ( a ^ { 4 } + a ^ { 3 } b + a ^ { 2 } b ^ { 2 } + a b ^ { 3 } + b ^ { 4 } \right ) \\ x ^ { 2 } + y ^ { 2 } + z ^ { 2 } - x y - y z - z x & = \frac { 1 } { 2 } \left [ ( x - y ) ^ { 2 } + ( y - z ) ^ { 2 } + ( z - x ) ^ { 2 } \right ] \end {aligned}$$

یک فرمول کلی برای محاسبه تفاضل توان‌های دو جمله به‌صورت زیر است:‌

$$\large a ^ { n } - b ^ { n } = ( a - b ) \left ( a ^ { n - 1 } + a ^ { n- 2 } b ^ { 1 } + a ^ { n - 3 } b ^ { 2 } + \ldots . + a ^ { 1 } b ^ { n - 2 } +b ^ { n - 1 } \right )$$

مثال تجزیه اتحاد ها

در این بخش، مثال‌های متنوعی از تجزیه اتحادها را بیان خواهیم کرد.

مثال اول تجزیه اتحاد ها

عبارت زیر را به کمک اتحادها تجزیه کنید:

$$\large x ^ 2 + 9 y ^ 2 – 25 m ^ 2 – 16 n ^ 2 + 16 x y + 4 0 m n$$

حل: با توجه به شکل این عبارت، باید جملاتی با متغیرهای دوتایی را مشخص کنیم. بدین منظور جملاتی که شامل $$x$$ یا $$y$$ هستند را در کنار هم و جملاتی که $$m$$ یا $$n$$ دارند را در کنار هم می‌آوریم و داریم:

$$\large x ^ 2 + 6 x y + 9 y ^ 2 - 25 m ^ 2 + 40 m n – 16 n ^ 2$$

جملات را می‌توان این‌گونه جدا کرد:

$$\large ( x^2 + 6 x y + 9 y ^ 2 ) – ( 2 5 m ^ 2 – 4 0 m n + 16 n ^ 2 )$$

که با استفاده از اتحاد مربع دوجمله‌ای می‌توان نوشت:

$$\large ( x + 3 y ) ^ 2 – ( 5 m - 4 n ) ^ 2$$

اکنون یک عبارت به‌فرم $$a^2 - b^ 2$$ داریم، که $$a = x + 3 y$$ و $$b = 5 m - 4 n$$. در این حالت، می‌توانیم از اتحاد مزدوج استفاده کنیم:

$$\large [ ( x + 3 y ) + ( 5 m - 4 n ) ] [ ( x + 3 y ) – ( 5 m – 4 n ) ]$$

و در نهایت، با ساده کرده عبارت‌های درون کروشه‌ها، خواهیم داشت:

$$\large ( x + 3 y + 5 m – 4 n ) ( x + 3 y – 5 m + 4 n )$$

مثال دوم تجزیه اتحاد ها

عبارت زیر را تجزیه کنید:

$$\large 2 x ^ 3 - x ^ 2 + x$$

حل: از $$x$$ فاکتور می‌گیریم و خواهیم داشت:

$$\large 2 x ^ 3 - x ^ 2 + x = x ( 2 x ^ 2 - x + 1 )$$

عبارت $$2 x ^ 2 - x + 1$$ را دیگر نمی‌توان تجزیه کرد و همان عبارت اخیر جواب این مسئله است.

مثال سوم تجزیه اتحاد ها

عبارت $$8 x ^ 3 + 2 7 y ^ 3 + 1 2 5 z ^ 3 – 6 0 x y z$$ را تجزیه کنید.

حل: این عبارت به‌فرم $$a ^ 3 + b ^ 3 + c ^ 3 – 3 a b c$$ است که در آن، $$a = 2 x$$، $$b = 3 y$$ و $$c = 5 z$$. می‌توانیم از اتحاد زیر استفاده کنیم:

$$\large a ^ 3 + b ^ 3 + c ^ 3 – 3 a b c = ( a + b + c ) ( a ^ 2 + b ^ 2 + c ^ 2 – a b – a c – b c )$$

در نتیجه، خواهیم داشت:

$$\large \begin {align} & 8 x ^ 3 + 27 y ^ 3 + 125 z ^ 3 – 60 x y z \\ & = ( 2 x + 3 y + 5 z ) [ ( 2 x ) ^ 2 + ( 3 y ) ^ 2 + ( 5 z ) ^ 2 – 2 x \cdot 3 y – 3 y \cdot 5 z – 2 x \cdot 5 z ] \\ & = ( 2 x + 3 y + 5 z ) ( 4 x ^ 2 + 9 y ^ 2 + 25 z ^ 2 – 6 x y – 1 5 y z – 1 0 x z ) \end {align}$$

مثال چهارم تجزیه اتحاد ها

عبارت $$25 x ^ 2 + 16 y ^ 2 + 9 z ^ 2 – 40 x y + 24 y z – 30 z x$$ را تجزیه کنید.

حل: این اتحاد به‌فرم $$a ^ 2 + b ^ 2 + c ^ 2 + 2 a b + 2 b c + 2 c a$$ است که در آن، $$a = 5 x$$، $$b = - 4 y$$ و $$c = - 3 z$$ است.

از اتحاد زیر استفاده می‌کنیم:

$$\large ( a + b + c ) ^ 2 = a ^ 2 + b ^ 2 + c ^ 2 + 2 a b + 2 b c + 2 c a$$

و خواهیم داشت:

$$\large 25 x ^ 2 + 16 y ^ 2 + 9 z ^ 2 – 40 x y + 24 y z – 30 z x = ( 5 x – 4 y – 3 z ) ^ 2$$

مثال پنجم تجزیه اتحاد ها

عبارت $$3 a ( { a } ^ { 2 } - 4 ) - 7 ( { a } ^ { 2 } - 4 )$$ را تجزیه کنید.

حل: از $$(a^ 2 - 4 )$$ فاکتور می‌گیریم و داریم:

$$\large 3 a ( { a } ^ { 2 } - 4 ) - 7 ( { a } ^ { 2 } - 4 ) = ( { a } ^ { 2 } - 4 ) ( 3 a - 7 )$$

اکنون، با استفاده از اتحاد مزدوج، می‌توانیم بنویسیم:

$$\large ( { a } ^ { 2 } - 4 ) ( 3 a - 7 ) = ( a - 2 ) ( a + 2 ) ( 3 a - 7 )$$

مثال ششم تجزیه اتحاد ها

عبارت $${a}^{3}-1$$ را تجزیه کنید.

حل: با استفاده از اتحاد تفاضل مکعب، به‌راحتی می‌توان این عبات را تجزیه کرد:

$$\large { a } ^ { 3 } - 1 = \left ( a - 1 \right ) \left ( { a } ^ { 2 } + a + 1 \right )$$

مثال هفتم تجزیه اتحاد ها

عبارت جبری $$16{y}^{3}-432$$ را تجزیه کنید.

حل: ابتدا از $$16$$ فاکتور می‌گیریم:

$$\large 1 6 { y } ^ { 3 } - 4 3 2 = 16 \left ( { y } ^ { 3 } - 2 7 \right )$$

جمله‌های داخل پرانتز دو مکعب کامل هستند و می‌توانیم از اتحاد تفاضل مکعب‌ها استفاده کنیم:

$$\large 16 \left ( { y } ^ { 3 } - 2 7 \right ) = 16 \left ( y - 3 \right ) \left ( { y } ^ { 2 } + 3 y + 9 \right )$$

مثال هشتم تجزیه اتحاد ها

عبارت $$8 { t } ^ { 3 } + 1 2 5{ p } ^ { 3 }$$ را تجزیه کنید.

حل: دو مکعب کامل داریم که با هم جمع شده‌اند. از اتحاد مجموع مکعب‌ها استفاده می‌کنیم و داریم:

$$\large \begin {align*} \left ( 8 { t } ^ { 3 } + 1 2 5 { p } ^ { 3 } \right ) & = \left ( 2 t + 5 p \right ) \left [ { \left ( 2 t \right ) } ^ { 2 } - \left ( 2 t \right ) \left ( 5 p \right ) + { \left ( 5 p \right ) } ^ { 2 } \right ] \\ & = \left ( 2 t + 5 p \right ) \left ( 4 { t } ^ { 2 } - 1 0 t p + 2 5 { p } ^ { 2 } \right ) \end {align*}$$

مثال نهم تجزیه اتحاد ها

عبارت $$3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 }$$ را تجزیه کنید.

حل: همان‌طور که مشاهده می‌کنیم، $$3x^2$$ در همه جملات مشترک است. در نتیجه، می‌توان از آن فاکتور گرفت و نوشت:‌

$$\large 3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 } = 3 { x ^ 2 } \left ( { { x ^ 2 } - x - 1 2 } \right )$$

با استفاده از اتحاد جمله مشترک، چندجمله‌ای این‌گونه تجزیه می‌شود:

$$\large 3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 } = 3 { x ^ 2 } \left ( { x - 4 } \right ) \left ( { x + 3 } \right )$$

مثال دهم تجزیه اتحاد ها

عبارت $${x^4} + {x^2} - 20$$ را تجزیه کنید.

حل: همان‌طور که مشاهده می‌کنیم، جمله $$x ^ 2$$ را می‌شود به‌عنوان یک متغیر در نظر گرفت که منجر به کار کردن با توان‌هایی پایین‌تر می‌شود تا تجزیه عبارت آسان‌تر شود. بنابراین، $$u = x ^ 2$$ را در نظر می‌گیریم. در نتیجه، $${u^2} = {\left( {{x^2}} \right)^2} = {x^4}$$ خواهد بود. بنابراین، چندجمله‌ای به صورت زیر در می‌آید:

$$\large { x ^ 4 } + { x ^ 2 } - 2 0 = { u ^ 2 } + u - 2 0$$

این چندجمله‌ای را می‌توان به صورت زیر تجزیه کرد:

$$\large \begin {align*} { x ^ 4 } + { x ^ 2 } - 2 0 & = { u ^ 2 } + u - 2 0 \\ & = \left ( { u - 4 } \right ) \left ( { u + 5 } \right ) \\ & = \left ( { { x ^ 2 } - 4 } \right ) \left ( { { x ^ 2 } + 5 } \right ) \end {align*}$$

اما این هنوز پایان کار نیست. می‌توانیم $$x ^ 2 - 4$$ را با استفاده از اتحاد مزدوج ساده کنیم. در نهایت، چندجمله‌ای مورد نظر به صورت زیر تجزیه خواهد شد:

$$\large { x ^ 4 } + { x ^ 2 } - 2 0 = \left ( { x - 2 } \right ) \left ( { x + 2 } \right ) \left ( { { x ^ 2 } + 5 } \right )$$

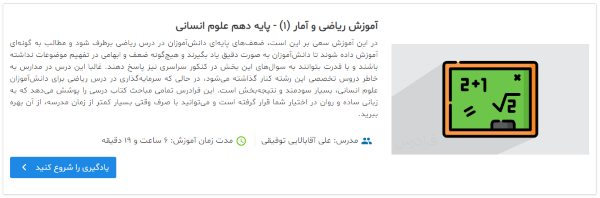
معرفی فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی

یکی از آموزش‌های ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانش‌آموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثال‌های حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و... پرداخته شده است. کار با داده‌های آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش داده‌ها ارائه شده است.

• برای مشاهده فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی + اینجا کلیک کنید.

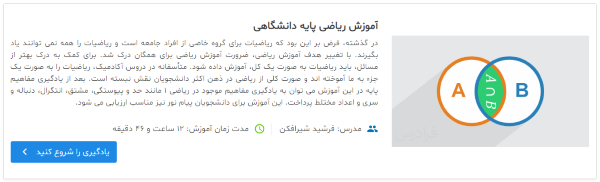
معرفی فیلم آموزش ریاضی پایه دانشگاهی

یکی از آموزش‌هایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه می‌توانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.

در درس اول، مجموعه‌ها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شده‌اند. موضوعات درس دوم، چندجمله‌ای‌ها و اتحاد و تجزیه است. در درس سوم، نامساوی‌ها، نامعادلات، طول پاره‌خط، ضریب زاویه و معادله خط مورد بحث قرار گرفته‌اند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شده‌اند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شده‌اند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفته‌اند.

• برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.

جمع‌بندی

در این آموزش، با کاربرد اتحادها در تجزیه عبارت‌های جبری آشنا شدیم. بدین صورت که با معرفی عبارت‌های جبری، مفهوم تجزیه آن‌ها را بیان کردیم. سپس، فهرستی از اتحادهای پرکاربرد را ارائه کردیم که در تجزیه عبارت‌های جبری کاربرد فراوانی دارند. در ادامه، مثال‌های متنوعی را از کاربرد اتحادها در تجزیه عبارت‌های جبری بررسی کردیم.