اتحاد مکعب دو جمله ای چیست؟ — اثبات، فرمول و مثال — به زبان ساده
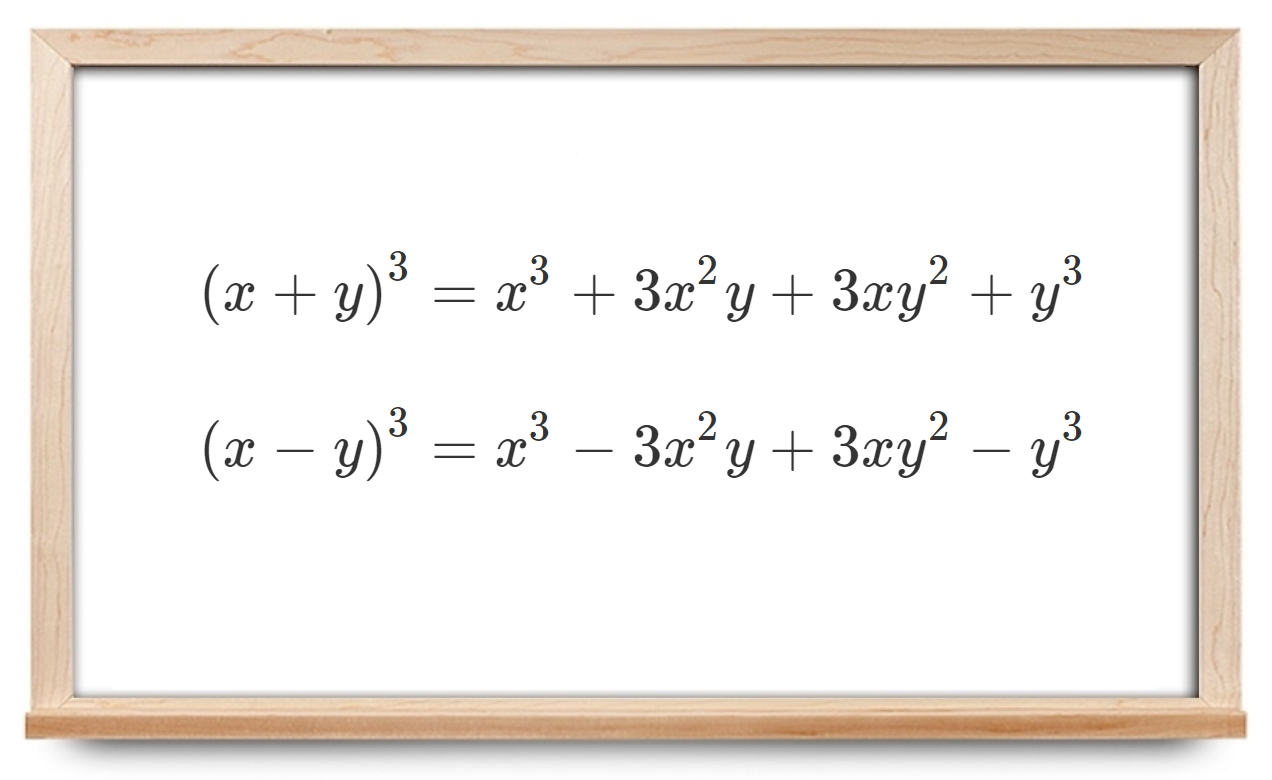
در آموزشهای پیشین از مجموعه مطالب ریاضی مجله فرادرس، با اتحاد و تجزیه آشنا شدیم. همچنین، در مطالبی، به طور خاص اتحادهای چاق و لاغر و مکعب را معرفی و در آموزش «نمونه سوال اتحاد و تجزیه — همراه با جواب» تعدادی مثال مربوط به اتحاد و تجزیه را حل کردیم. در این آموزش، با اتحاد مکعب دو جمله ای آشنا میشویم و علاوه بر بیان اثبات آن، تعدادی مثال را نیز حل خواهیم کرد.
اتحاد مکعب دو جمله ای چیست ؟
اتحاد مکعب دو جمله ای، همانطور که نامش نشان میدهد، اتحادی است که برای مکعب یا توان سوم مجموع یا تفاضل دو جمله بیان میشود. در ادامه، اتحاد مکعب دو جمله ای را برای دو حالت مجموع و تفاضل بیان میکنیم.
اتحاد مکعب دو جمله ای مجموع
حتماً میدانید که مکعب یک جسم هندسی است که حجم آن را میتوان با به توان ۳ رساندن طول هر ضلعش محاسبه کرد. در اتحاد مکعب دو جمله ای نیز، مکعب به مفهوم توان ۳ است. بدین ترتیب، اتحاد مکعب دو جمله ای مجموع یعنی اتحاد مجموع دو جمله به توان ۳. اگر بخواهیم این موضوع را به صورت ریاضی بیان کنیم، فرض کنید دو جمله $$ a $$ و $$ b $$ را داریم. در این صورت، اتحاد مکعب دو جمله ای مجموع به شکل زیر بیان میشود:
$$ \large \boxed { \begin {aligned} ( a + b ) ^ 3 & = a ^ 3 + 3 a ^ 2 b + 3 a b ^ 2 + b ^ 3 \end {aligned} } $$
دقت کنید که اتحاد مکعب مجموع دو جمله ای را با اتحاد چاق و لاغر اشتباه نگیرید. اتحاد چاق و لاغر به صورت زیر است:
$$ \large { \begin {aligned} a ^ 3 + b ^ 3 & = ( a + b ) ( a ^ 2 - a b + b ^ 2 ) \end {aligned} } $$
اتحاد مکعب دو جمله ای تفاضل
اتحاد مکعب دو جمله ای تفاضل، همانگونه که از نامش پیداست، برای تفاضل دو جمله بیان میشود و به صورت زیر است:
$$ \large \boxed { \begin {aligned} ( a - y ) ^ 3 & = a ^ 3 - 3 a ^ 2 b + 3 a b ^ 2 - b ^ 3 \end {aligned} } $$
باز هم توجه کنید که اتحاد چاق و لاغر زیر را با این اتحاد دو جمله ای اشتباه نگیرید:
$$ \large { \begin {aligned} a ^ 3 - b ^ 3 & = ( a - b ) ( a ^ 2 + a b + b ^ 2 ) \end {aligned} } $$
فرمول اتحاد مکعب دو جمله ای
به طور خلاصه، فرمول اتحاد مکعب دو جمله ای برای دو حالت مجموع و تفاضل به صورت زیر است:
$$ \large \boxed { \begin {aligned} ( a + b ) ^ 3 & = a ^ 3 + 3 a ^ 2 b + 3 a b ^ 2 + b ^ 3 \\ ( a - b ) ^ 3 & = a ^ 3 - 3 a ^ 2 b + 3 a b ^ 2 - b ^ 3 \end {aligned} } $$
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
اثبات اتحاد مکعب دو جمله ای مجموع
اثبات اتحاد مکعب دو جمله ای مجموع $$a$$ و $$ b $$ را میتوان به روش جبری در سه مرحله ساده بیان کرد. باید تساوی زیر را اثبات کنیم:
$$ \large { \begin {aligned} ( a + b ) ^ 3 & = a ^ 3 + 3 a ^ 2 b + 3 a b ^ 2 + b ^ 3 \end {aligned} } $$
مرحله ۱. ابتدا از سمت چپ تساوی شروع میکنیم. دوجملهای $$a+b$$ را به توان ۳ میرسانیم (سه بار در خودش ضرب میکنیم). در نتیجه، مکعب مجموع دو جمله $$a$$ و $$b$$ را میتوان به فرم زیر بیان کرد:
$$ \large ( a + b ) ^ { 3 } = ( a + b ) \times ( a + b ) \times ( a + b ) $$
مرحله ۲. نمیتوانیم همزمان سه دوجملهای را در یکدیگر ضرب کنیم. به همین دلیل، ابتدا دو تا از آنها را در یکدیگر ضرب میکنیم و سپس جواب این ضرب را در دوجملهای سوم ضرب میکنیم. بنابراین، خواهیم داشت:
$$ \large \begin {array} { l }
\;\;\;\;\;\;\,( a + b ) ^ { 3 } = ( a + b ) \times ( ( a + b ) \times ( a + b ) ) \\
\Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times ( a \times ( a + b ) + b \times ( a + b ) ) \\
\Longrightarrow ( a + b ) ^ { 3 } = ( a +b ) \times ( a \times a + a \times b + b \times a + b \times b ) \\
\Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + a b + b a + b ^ { 2 } \right ) \\
\Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + a b + a b + b ^ { 2 } \right ) \\
\Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right )
\end {array} $$
مرحله ۳. اکنون مجموع دو جمله $$a+b$$ را در بسط مربع مجموع دو جمله ضرب میکنیم:
$$ \large \begin {array} {ll}
\Longrightarrow & ( a + b ) ^ { 3 } = a \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right ) + b \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right ) \\
\Longrightarrow & ( a + b ) ^ { 3 } = a \times a ^ { 2 } + a \times 2 a b + a \times b ^ { 2 } + b \times a ^ { 2 } + b \times 2 a b + b \times b ^ { 2 } \\
\Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + 2 a ^ { 2 } b + a b ^ { 2 } + b a ^ { 2 } + 2 a b ^ { 2 } + b ^ { 3 } \\
\Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + 2 a ^ { 2 } b + a b ^ { 2 } + a ^ { 2 } b + 2 a b ^ { 2 } + b ^ { 3 } \\
\Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + b ^ { 3 } + 2 a ^ { 2 } b + a ^ { 2 } b + a b ^ { 2 } + 2 a b ^ { 2 } \\
\quad & ( a + b ) ^ { 3 } = a ^ { 3 } + b ^ { 3 } + 3 a ^ { 2 } b + 3 a b ^ { 2 }
\end {array} $$
بنابراین به عبارت مورد نظر میرسیم و اثبات کامل میشود.
با سادهسازی جبری، تساوی را میتوان به صورت زیر نیز نوشت:
$$ \large ( a + b ) ^ { 3 } = a ^ 3 + b ^ 3 + 3 a b ( a + b ) $$
اثبات اتحاد مکعب دو جمله ای تفاضل
اثبات اتحاد مکعب دو جمله ای تفاضل $$a$$ و $$ b $$ را میتوان به روش جبری در سه مرحله ساده بیان کرد. باید تساوی زیر را اثبات کنیم:
$$ \large { \begin {aligned} ( a - b ) ^ 3 & = a ^ 3 - 3 a ^ 2 b + 3 a b ^ 2 - b ^ 3 \end {aligned} } $$
مرحله ۱. ابتدا از سمت چپ تساوی شروع میکنیم. دوجملهای $$a-b$$ را به توان ۳ میرسانیم (سه بار در خودش ضرب میکنیم). در نتیجه، مکعب مجموع دو جمله $$a$$ و $$b$$ را میتوان به فرم زیر بیان کرد:
$$ \large ( a - b ) ^ { 3 } = ( a - b ) \times ( a - b ) \times ( a - b ) $$
مرحله ۲. نمیتوانیم همزمان سه دوجملهای را در یکدیگر ضرب کنیم. به همین دلیل، ابتدا دو تا از آنها را در یکدیگر ضرب میکنیم و سپس جواب این ضرب را در دوجملهای سوم ضرب میکنیم. در نتیجه، خواهیم داشت:
$$ \large \begin {array} { l }
\;\;\;\;\;\;\,( a - b ) ^ { 3 } = ( a - b ) \times ( ( a - b ) \times ( a - b ) ) \\
\Longrightarrow ( a - b ) ^ { 3 } = ( a - b ) \times ( a \times ( a - b ) - b \times ( a - b ) ) \\
\Longrightarrow ( a - b ) ^ { 3 } = ( a -b ) \times ( a \times a - a \times b - b \times a + b \times b ) \\
\Longrightarrow ( a - b ) ^ { 3 } = ( a - b ) \times \left ( a ^ { 2 } - a b - b a + b ^ { 2 } \right ) \\
\Longrightarrow ( a - b ) ^ { 3 } = ( a - b ) \times \left ( a ^ { 2 } - a b - a b + b ^ { 2 } \right ) \\
\Longrightarrow ( a - b ) ^ { 3 } = ( a - b ) \times \left ( a ^ { 2 } - 2 a b + b ^ { 2 } \right )
\end {array} $$
مرحله ۳. اکنون مجموع دو جمله $$a-b$$ را در بسط مربع مجموع دو جمله ضرب میکنیم:
$$ \large \begin {array} {ll}
\Longrightarrow & ( a - b ) ^ { 3 } = a \times \left ( a ^ { 2 } - 2 a b + b ^ { 2 } \right ) - b \times \left ( a ^ { 2 } - 2 a b + b ^ { 2 } \right ) \\
\Longrightarrow & ( a - b ) ^ { 3 } = a \times a ^ { 2 } - a \times 2 a b + a \times b ^ { 2 } - b \times a ^ { 2 } + b \times 2 a b - b \times b ^ { 2 } \\
\Longrightarrow & ( a - b ) ^ { 3 } = a ^ { 3 } - 2 a ^ { 2 } b + a b ^ { 2 } - b a ^ { 2 } + 2 a b ^ { 2 } - b ^ { 3 } \\
\Longrightarrow & ( a - b ) ^ { 3 } = a ^ { 3 } - 2 a ^ { 2 } b + a b ^ { 2 } - a ^ { 2 } b + 2 a b ^ { 2 } - b ^ { 3 } \\
\Longrightarrow & ( a - b ) ^ { 3 } = a ^ { 3 } - b ^ { 3 } - 2 a ^ { 2 } b - a ^ { 2 } b + a b ^ { 2 } + 2 a b ^ { 2 } \\
\quad & ( a - b ) ^ { 3 } = a ^ { 3 } - b ^ { 3 } - 3 a ^ { 2 } b + 3 a b ^ { 2 }
\end {array} $$
بنابراین به عبارت مورد نظر میرسیم و اثبات کامل میشود.
با سادهسازی جبری، تساوی را میتوان به صورت زیر نیز نوشت:
$$ \large ( a + b ) ^ { 3 } = a ^ 3 - b ^ 3 - 3 a b ( a - b ) $$
تعبیر هندسی اتحاد مکعب دو جمله ای
شکل زیر تعبیر هندسی اتحاد مکعب دو جمله ای مجموع را نشان میدهد.

مثال های اتحاد مکعب دو جمله ای
در این بخش، چند مثال را از اتحاد مکعب دو جمله ای حل میکنیم.
مثال اول اتحاد مکعب دو جمله ای
عبارت زیر را $$(x+2)^3$$ را ساده کنید.
حل: با در نظر گرفتن دو جمله $$2$$ و $$ x$$، از اتحاد مکعب مجموع دو جمله استفاده میکنیم و داریم:
$$ \large ( x + 2 ) ^ 3 = x ^ 3 + 3 \times x ^ 2 \times 2 + 3 \times x \times 2 ^ 2 + 2 ^ 3 = x ^ 3 + 6 x ^ 2 + 12 x + 8 $$
مثال دوم اتحاد مکعب دو جمله ای
عبارت $$(2a-b)^3$$ را ساده کنید.
حل: در اینجا از اتحاد مکعب دو جمله ای تفاضل استفاده میکنیم و داریم:
$$ \large \begin {aligned} ( 2 a - b ) ^ 3 & = (2 a) ^ 3 - 3 \times (2a) ^ 2 \times b + 3 \times (2a) \times b ^ 2 - b ^ 3 \\ & = 8a ^ 3 - 12 a ^ 2 b + 6 a b ^ 2 - b ^ 3 \end {aligned} $$
مثال سوم اتحاد مکعب دو جمله ای
عبارت $$x^3 + 8$$ را تجزیه کنید.
حل: این عبارت را میتوان به صورت $$x^ 3 + 2 ^ 3 $$ نوشت. همان طور که میبینیم، ظاهر این عبارت شبیه اتحاد چاق و لاغر است، نه اتحاد دو جمله ای. بنابراین، از اتحاد چاق و لاغر استفاده میکنیم:
$$ \large x ^ 3 + 8 = ( x + 2 ) ( x ^ 2 - 2 x + 2 ^ 2 ) = ( x + 2 ) ( x ^ 2 - 2 x + 4 ) $$
مثال چهارم اتحاد مکعب دو جمله ای
عبارت زیر را ساده کنید:
$$ \large ( x + y ) ^ 3 + ( x - y ) ^ 3 $$
حل: اگر به بسط این عبارتها دقت کنیم، میبینیم که جملات دوم و چهارم حذف میشوند و میتوان جملات اول و سوم را با هم ترکیب کرد. یعنی اگر داشته باشیم:
$$ \large \begin {aligned} ( x + y ) ^ 3 & = x ^ 3 + 3 x ^ 2 y + 3 x y ^ 2 + y ^ 3 \\ ( x - y ) ^ 3 & = x ^ 3 - 3 x ^ 2 y + 3 x y ^ 2 - y ^ 3 \end {aligned} $$
مجموع آنها برابر خواهد بود با:
$$ \large ( x + y ) ^ 3 + ( x - y ) ^ 3 = 2 x ^ 3 + 6 x y ^ 2 $$
یک روش دیگر برای حل این مثال، استفاده از اتحاد مجموع دو مکعب است:
$$ \large \begin {aligned} ( x + y ) ^ 3 + ( x - y ) ^ 3 & = \big [ ( x + y ) + ( x - y ) \big ] \big [ ( x + y ) ^ 2 - ( x + y ) ( x - y ) + ( x - y ) ^ 2 \big] \\ & = 2 x \times \big [ x ^ 2 + 3 y ^ 2 \big ] \\ & = 2 x ^ 3 + 6 x y ^ 2 \end {aligned} $$
مثال پنجم اتحاد مکعب دو جمله ای
فرض کنید دو عدد حقیقی $$x$$ و $$y$$ داده شدهاند. مجموع این دو عدد $$x+y=7$$ و مجموع مکعب آنها $$ x ^ 3 + y ^ 3 = 133 $$ است. مقدار $$xy$$ را به دست آورید.
حل: تساوی زیر را از قبل میدانیم:
$$ \large x ^ 3 + y ^ 3 = ( x + y ) ( x ^ 2 + y ^ 2 -x y ) $$
با قرار دادن اطلاعات مسئله در این رابطه، خواهیم داشت:
$$ \large 133 = 7 ( x ^ 2 + y ^ 2 + 2 x y -3 x y) \\
19 = (x + y)^2 - 3xy \\
19 = 49 − 3 xy \\
30 = 3xy \\
10=xy $$
بنابراین، $$xy = 10 $$ به دست میآید.
مثال ششم اتحاد مکعب دو جمله ای
عبارت زیر را محاسبه کنید:
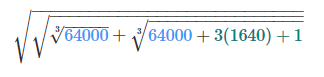
حل: عدد ۶۴۰۰۰ را میتوان به صورت زیر نوشت:
$$ \large 64000 = 6 4 \times { 1 0 } ^{ 3 } = {2 } ^ { 6 } \times { 1 0 } ^ { 3 } = { { \left ( { { 2 } ^ { 2 } } \right ) } ^ { 3 } } \times { { 1 0 } ^ { 3 } } \\ \Rightarrow
\sqrt [ 3 ] { 6 4 0 0 0 } = \sqrt [ 3 ] { { { \left ( { { 2 } ^ { 2 } } \right ) } ^ { 3 } } \times { { 1 0 } ^ { 3 } } } = { 2 } ^ { 2 } \times 10 = 40 $$
همچنین، داریم:
$$\large \sqrt[3]{64000+3(1640)+1}= \sqrt[3]{68921}=\sqrt[3]{{41}^{3}}=41 $$
در نتیجه، جواب عبارت برابر است با:
$$ \large \sqrt {\sqrt{40+41}}=\sqrt{\sqrt {81}}=\sqrt {9} = 3 $$
مثال هفتم اتحاد مکعب دو جمله ای
یکی از پاسخهای معادله زیر به فرم $$\frac ab $$ است که در آن، $$ a $$ و $$b$$ اعدادی صحیح و نسبت به هم اول هستند. مقدار $$a+b$$ را بیابید.
$$\large \sqrt[3]{ 1+ \sqrt{x}} + \sqrt[3]{1 - \sqrt{x}} = \sqrt[3]{5}$$
حل: دو عبارت $$ \alpha = \sqrt [ 3 ] { 1 + \sqrt { x } } $$ و $$ \beta = \sqrt [ 3 ] { 1 - \sqrt { x } } $$ را در نظر بگیرید. بنابراین، داریم:
$$ \large ( \alpha + \beta ) ^ 3 = 5 \\ \Rightarrow
\alpha ^ 3 + 3 \alpha ^ 2 \beta + 3 \alpha \beta ^ 2 + \beta ^ 3 = 5 $$
از طرفی، داریم:
$$ \large \alpha ^ 3 + \beta ^ 3 = 1 + \sqrt { x } + 1 - \sqrt { x } = 2 $$
بنابراین، میتوان نوشت:
$$\large 2 + 3 \alpha \beta ( \alpha + \beta ) = 5 \\ \Rightarrow 3 \alpha \beta ( \alpha + \beta ) = 3 \\ \Rightarrow \alpha \beta ( \alpha + \beta ) = 1 $$
اکنون دو طرف تساوی اخیر را به توان ۳ میرسانیم:
$$ \large \alpha ^ 3 \beta ^ 3 ( \alpha + \beta ) ^ 3 = 1 $$
در نتیجه، داریم:
$$ \large ( 1 + \sqrt { x } ) ( 1 - \sqrt { x } ) ( 5 ) = 1
\Rightarrow 5(1-x) = 1 \\ \Rightarrow 1 - x = \dfrac {1}{5} \Rightarrow x = \frac {4}{5} = \frac {a}{b} \Rightarrow a + b = \boxed {9} $$
مثال هشتم اتحاد مکعب دو جمله ای
مقدار $$107 ^ 3 $$ را محاسبه کنید.
حل: این عبارت را میتوان به صورت زیر نوشت:
$$\large 107^ 3 = (100+7)^ 3 $$
اکنون از اتحاد مکعب دو جمله ای استفاده میکنیم:
$$\large (a+b)^3 = a ^ 3 + b ^ 3 + 3 a b (a+b)$$
با قرار دادن $$ a = 100$$ و $$ b = 7 $$، میتوان نوشت:
$$\large ( 100 + 7 ) ^ 3 = 100 ^ 3 + 7^ 3 + 3(100)(7)(100 + 7)\\
(100 + 7)^ 3 = 1000000 + 343 + 3(100)(7)(107) \\
(100 + 7)^ 3 = 1000000 + 343 + 224700 \\
(107 ) ^ 3 = 1225043 $$
در نتیجه، مقدار $$107^ 3$$ برابر است با $$1,225,043$$.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزشهایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه میتوانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعهها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شدهاند. موضوعات درس دوم، چندجملهایها و اتحاد و تجزیه است. در درس سوم، نامساویها، نامعادلات، طول پارهخط، ضریب زاویه و معادله خط مورد بحث قرار گرفتهاند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شدهاند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شدهاند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفتهاند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.











با سلام وضمن تشکر از سایت بی نظیر شما عذرمیخوام در مثال پنج از اتحاد مکعب دو جمله ای استفاده نشده از اتحاد چاق و لاغر بدست امده که من وقتی به اتحاد مکعب دو جمله رفتم جواب منفی 4 بدست آمده
سلام و وقت بخیر؛
زمانی که مجموع x و y به توان سه برسند (جمع x و y به توان ۳)، از اتحاد مکعب دوجملهای استفاده میکنیم. در اینجا، x به طور جداگانه به توان ۳ رسیده و y نیز به طور جداگانه به توان ۳ رسیده و این دو با هم جمع شدهاند. در این حالت، باید از اتحاد چاق و لاغر استفاده کرد. برای آشنایی بیشتر با تفاوت این دو ااحاد، مطالعه مطلب «اتحاد مکعب دو جمله ای چیست؟ — اثبات، فرمول و مثال — به زبان ساده» را به شما پیشنهاد میکنیم.
از همراهیتان با مجله فرادرس سپاسگزاریم
سلام و عرض ادب خدمت شما جناب مهندس حمیدی. ضمن تشکر از زحمات شما عرض کنم که در مثال دوم صورت سوال آ منهای دو بی به توان سه هست که در قسمت حل تبدیل شده به دو آ منهای بی به توان سه و مثال سوم هم به همین شکل صورت سوال در قسمت حل عوض شده.
در مثال پنجم در قسمت حل فرمودید:
با قرار دادن اطلاعات مسئله در این رابطه خواهیم داشت:
همون خط اول مثبت دو ایکس وای، و منفی سه ایکس وای از کجا به دست میاد؟*
لطفا راهنمایی کنید برای اعداد بزرگی مثل عدد رادیکال شصت و هشت هزار و نهصد و بیست و یک با فرجه ی سه، چطوری به عدد چهل و یک به توان سه برسیم؟
مثال هفتم رو اگر امکانش هست لطف کنید توضیح فارسی بیشتری براش بنویسید، سوال واقعا سختی هست. تشکر.
سلام میلاد عزیز.
موارد اول و دوم تصحیح شد. در مورد سوم، به این دلیل $$-xy$$ را بهشکل $$ -3xy+2xy$$ نوشتهایم که به اتحاد مربع دوجملهای برسیم، زیرا مقدار $$ x + y $$ را داریم. برای مورد چهارم، میتوان از اتحاد مکعب دوجملهای کمک گرفت. در مثال هفتم تکنیکهای بسیار جزئیای به کار رفته که تنها با حل تمرینهای زیاد بر آنها مسلط خواهید شد. پیشنهاد میکنیم این مسئله را چند بار مطالعه و سعی کنید خودتان آن را حل کنید.
سپاس از همراهیتان.