اتحاد مکعب چیست؟ – فرمول، اثبات و مثال به زبان ساده

در آموزش‌های پیشین مجله فرادس، با اتحاد و تجزیه آشنا شدیم و اتحادهای مهم را معرفی کردیم. همچنین در مطلب «نمونه سوال اتحاد و تجزیه — همراه با جواب» از مجله فرادرس چند مثال را درباره اتحادها حل کردیم. در این آموزش، به یکی از اتحادهای مهم و کاربردی، به نام اتحاد مکعب می‌پردازیم و مثال‌هایی از آن را حل خواهیم کرد.

اتحاد مکعب مجموع

همان‌طور که می‌دانیم مکعب یک حجم هندسی است که حجم آن از به توان ۳ رساندن طول هر ضلع آن به دست می‌آید. در اینجا هم مکعب به معنای توان ۳ است. اتحاد مکعب مجموع یعنی اتحاد مجموع دو جمله به توان ۳. به بیان ریاضی، فرض کنید دو جمله $$x$$ و $$y$$ را داریم. اتحاد مکعب مجموع این دو جمله به صورت زیر خواهد بود:

$$\boxed { \begin {aligned} ( x + y ) ^ 3 & = x ^ 3 + 3 x ^ 2 y + 3 x y ^ 2 + y ^ 3 \end {aligned} }$$

دقت کنید که اتحاد مکعب مجموع را با اتحاد چاق و لاغر اشتباه نگیرید:

$${ \begin {aligned} x ^ 3 + y ^ 3 & = ( x + y ) ( x ^ 2 - x y + y ^ 2 ) \end {aligned} }$$

اتحاد مکعب تفاضل

اتحاد مکعب تفاضل، همان‌گونه که از نامش مشخص است، برای تفاضل دو جمله بیان می‌شود و به صورت زیر است:

$$\boxed { \begin {aligned} ( x - y ) ^ 3 & = x ^ 3 - 3 x ^ 2 y + 3 x y ^ 2 - y ^ 3 \end {aligned} }$$

توجه کنید که اتحاد چاق و لاغر زیر را با این اتحاد اشتباه نگیرید:‌

$${ \begin {aligned} x ^ 3 - y ^ 3 & = ( x - y ) ( x ^ 2 + x y + y ^ 2 ) \end {aligned} }$$

اتحاد مکعب دو جمله ای

آنچه در بخش‌های قبل گفتیم، چون مربوط به دو جمله بود، به آن‌ها اتحاد مکعب دو جمله ای می‌گوییم که به صورت زیر هستند:

$$\boxed { \begin {aligned} ( x + y ) ^ 3 & = x ^ 3 + 3 x ^ 2 y + 3 x y ^ 2 + y ^ 3 \\ ( x - y ) ^ 3 & = x ^ 3 - 3 x ^ 2 y + 3 x y ^ 2 - y ^ 3 \end {aligned} }$$

برای آشنایی بیشتر با اتحاد مکعب دوجمله‌‌ای، به آموزش «اتحاد مکعب دوجمله‌ای چیست؟ — اثبات، فرمول و مثال — به زبان ساده» در این لینک مراجعه کنید.

اثبات اتحاد مکعب دو جمله ای

اثبات اتحاد مکعب مجموع دو جمله $$a$$ و $$b$$ را می‌توان به روش جبری در سه گام ساده انجام داد.

فیلم آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی در فرادرس

کلیک کنید

گام ۱. نخست، دوجمله‌ای $$a+b$$ را در سه بار در خودش ضرب می‌کنیم که از نظر ریاضی به معنی همان مکعب دوجمله‌ای است. بنابراین، مکعب مجموع دو جمله $$a$$ و $$b$$ را می‌توان به فرم زیر بیان کرد:

$$( a + b ) ^ { 3 } = ( a + b ) \times ( a + b ) \times ( a + b )$$

گام ۲. نمی‌توانیم همزمان سه دوجمله‌ای را در یکدیگر ضرب کنیم. بنابراین، ابتدا دو تا از آن‌ها را در یکدیگر ضرب می‌کنیم و سپس حاصل آن‌ها را در دوجمله‌ای سوم ضرب می‌کنیم. بنابراین، خواهیم داشت:

$$\begin {array} { l } \;\;\;\;\;\;\,( a + b ) ^ { 3 } = ( a + b ) \times ( ( a + b ) \times ( a + b ) ) \\ \Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times ( a \times ( a + b ) + b \times ( a + b ) ) \\ \Longrightarrow ( a + b ) ^ { 3 } = ( a +b ) \times ( a \times a + a \times b + b \times a + b \times b ) \\ \Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + a b + b a + b ^ { 2 } \right ) \\ \Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + a b + a b + b ^ { 2 } \right ) \\ \Longrightarrow ( a + b ) ^ { 3 } = ( a + b ) \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right ) \end {array}$$

گام ۳. اکنون مجموع دو جمله $$a+b$$ را در بسط مربع مجموع دو جمله ضرب می‌کنیم:

$$\begin {array} {ll} \Longrightarrow & ( a + b ) ^ { 3 } = a \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right ) + b \times \left ( a ^ { 2 } + 2 a b + b ^ { 2 } \right ) \\ \Longrightarrow & ( a + b ) ^ { 3 } = a \times a ^ { 2 } + a \times 2 a b + a \times b ^ { 2 } + b \times a ^ { 2 } + b \times 2 a b + b \times b ^ { 2 } \\ \Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + 2 a ^ { 2 } b + a b ^ { 2 } + b a ^ { 2 } + 2 a b ^ { 2 } + b ^ { 3 } \\ \Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + 2 a ^ { 2 } b + a b ^ { 2 } + a ^ { 2 } b + 2 a b ^ { 2 } + b ^ { 3 } \\ \Longrightarrow & ( a + b ) ^ { 3 } = a ^ { 3 } + b ^ { 3 } + 2 a ^ { 2 } b + a ^ { 2 } b + a b ^ { 2 } + 2 a b ^ { 2 } \\ \quad & ( a + b ) ^ { 3 } = a ^ { 3 } + b ^ { 3 } + 3 a ^ { 2 } b + 3 a b ^ { 2 } \end {array}$$

بنابراین به عبارت مورد نظر می‌رسیم و اثبات کامل می‌شود.

با ساده‌سازی جبری، تساوی را می‌توان به صورت زیر نیز نوشت:

$$( a + b ) ^ { 3 } = a ^ 3 + b ^ 3 + 3 a b ( a + b )$$

شکل زیر تعبیر هندسی اتحاد مکعب را نشان می‌دهد.

اتحاد مکعب سه جمله ای

اتحاد مکعب سه جمله ای با استفاده از اتحاد مکعب دو جمله ای و به صورت زیر محاسبه می‌شود:

$$\begin{array}{l} (a+b+c)^{3} \\ =[a+(b+c)]^{3} \\ =a^{3}+3 a(b+c)[a+(b+c)]+(b+c)^{3} \\ =a^{3}+3 a(b+c)[a+(b+c)]+b^{3}+3 b c(b+c)+c^{3} \\ =a^{3}+b^{3}+c^{3}+3 a(b+c)[a+(b+c)]+3 b c(b+c) \\ =a^{3}+b^{3}+c^{3}+3(b+c)\left[a^{2}+a b+a c+b c\right] \\ =a^{3}+b^{3}+c^{3}+3(b+c)[a(a+b)+c(a+b)] \\ =a^{3}+b^{3}+c^{3}+3(b+c)(a+b)(a+c) \end{array}$$

این فرمول را می‌توان به صورت زیر نیز نوشت:

$$(a+b+c)^{3}-a^{3}-b^{3}-c^{3}=3(b+c)(a+b)(a+c)$$

مثال های اتحاد مکعب

در این بخش، چند مثال را از اتحاد مکعب حل می‌کنیم.

مثال اول اتحاد مکعب

بسط عبارت $$(x+1)^3$$ را بنویسید.

حل: با در نظر گرفتن دو جمله $$1$$ و $$x$$، از اتحاد مکعب مجموع دو جمله استفاده می‌کنیم و خواهیم داشت:

$$( x + 1 ) ^ 3 = x ^ 3 + 3 \times x ^ 2 \times 1 + 3 \times x \times 1 ^ 2 + 1 ^ 3 = x ^ 3 + 3 x ^ 2 + 3 x + 1$$

مثال دوم اتحاد مکعب

حاصل عبارت $$(a-2b)^3$$ را بنویسید.

حل: با استفاده از اتحاد مکعب، می‌توان نوشت:

$$\begin {aligned} ( a - 2 b ) ^ 3 & = a ^ 3 - 3 \times a ^ 2 \times ( 2 b ) + 3 \times a \times ( 2 b ) ^ 2 - ( 2 b ) ^ 3 \\ & = a ^ 3 - 6 a ^ 2 b + 12 a b ^ 2 - 8 b ^ 3 \end {aligned}$$

مثال سوم اتحاد مکعب

عبارت $$x^3 + 8$$ را تجزیه کنید.

حل: این عبارت را می‌توان به صورت $$x^ 3 + 2 ^ 3$$ نوشت. در نتیجه، می‌توان از اتحاد چاق و لاغر جمله استفاده کرد و نوشت:

$$x ^ 3 + 8 = ( x + 2 ) ( x ^ 2 - 2 x + 2 ^ 2 ) = ( x + 2 ) ( x ^ 2 - 2 x + 4 )$$

مثال چهارم اتحاد مکعب

حاصل عبارت زیر را به دست آورید:

$$( x + y ) ^ 3 + ( x - y ) ^ 3$$

حل: اگر به بسط این عبارت دقت کنیم، می‌بینیم که جملات دوم و چهارم حذف می‌شوند و می‌توان جملات اول و سوم را با هم ترکیب کرد. یعنی اگر داشته باشیم:

$$\begin {aligned} ( x + y ) ^ 3 & = x ^ 3 + 3 x ^ 2 y + 3 x y ^ 2 + y ^ 3 \\ ( x - y ) ^ 3 & = x ^ 3 - 3 x ^ 2 y + 3 x y ^ 2 - y ^ 3 \end {aligned}$$

مجموع آن‌ها برابر خواهد بود با:

$$( x + y ) ^ 3 + ( x - y ) ^ 3 = 2 x ^ 3 + 6 x y ^ 2$$

یک روش دیگر برای حل مثال، این است که از اتحاد مجموع دو مکعب استفاده کنیم:

$$\begin {aligned} ( x + y ) ^ 3 + ( x - y ) ^ 3 & = \big [ ( x + y ) + ( x - y ) \big ] \big [ ( x + y ) ^ 2 - ( x + y ) ( x - y ) + ( x - y ) ^ 2 \big] \\ & = 2 x \times \big [ x ^ 2 + 3 y ^ 2 \big ] \\ & = 2 x ^ 3 + 6 x y ^ 2 \end {aligned}$$

مثال پنجم اتحاد مکعب

دو عدد حقیقی $$x$$ و $$y$$ را در نظر بگیرید که مجموع آن‌ها $$x+y=7$$ و مجموع مکعب آن‌ها $$x ^ 3 + y ^ 3 = 133$$‌ است. مقدار $$xy$$ را محاسبه کنید.

حل: تساوی زیر را از قبل می‌دانیم:

$$x ^ 3 + y ^ 3 = ( x + y ) ( x ^ 2 + y ^ 2 -x y )$$

با قرار دادن اطلاعات مسئله در این رابطه، خواهیم داشت:

$$133 = 7 ( x ^ 2 + y ^ 2 + 2 x y -3 x y) \\ 19 = (x + y)^2 - 3xy \\ 19 = 49 − 3 xy \\ 30 = 3xy \\ 10=xy$$

بنابراین، $$xy = 10$$ به دست می‌آید.

مثال ششم اتحاد مکعب

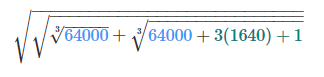
حاصل عبارت زیر را به دست آورید:

حل:‌ عدد ۶۴۰۰۰ را می‌توان به صورت زیر نوشت:

$$64000 = 6 4 \times { 1 0 } ^{ 3 } = {2 } ^ { 6 } \times { 1 0 } ^ { 3 } = { { \left ( { { 2 } ^ { 2 } } \right ) } ^ { 3 } } \times { { 1 0 } ^ { 3 } } \\ \Rightarrow \sqrt [ 3 ] { 6 4 0 0 0 } = \sqrt [ 3 ] { { { \left ( { { 2 } ^ { 2 } } \right ) } ^ { 3 } } \times { { 1 0 } ^ { 3 } } } = { 2 } ^ { 2 } \times 10 = 40$$

همچنین، داریم:

$$\sqrt[3]{64000+3(1640)+1}= \sqrt[3]{68921}=\sqrt[3]{{41}^{3}}=41$$

در نتیجه، حاصل عبارت برابر است با:

$$\sqrt {\sqrt{40+41}}=\sqrt{\sqrt {81}}=\sqrt {9} = 3$$

مثال هفتم اتحاد مکعب

یکی از جواب‌های معادله زیر به فرم $$\frac ab$$ است که در آن، $$a$$ و $$b$$ اعدادی صحیح و نسبت به هم اول هستند. مقدار $$a+b$$ را بیابید.

$$\sqrt[3]{ 1+ \sqrt{x}} + \sqrt[3]{1 - \sqrt{x}} = \sqrt[3]{5}$$

حل: دو عبارت $$\alpha = \sqrt [ 3 ] { 1 + \sqrt { x } }$$ و $$\beta = \sqrt [ 3 ] { 1 - \sqrt { x } }$$ را در نظر بگیرید. بنابراین، داریم:

$$( \alpha + \beta ) ^ 3 = 5 \\ \Rightarrow \alpha ^ 3 + 3 \alpha ^ 2 \beta + 3 \alpha \beta ^ 2 + \beta ^ 3 = 5$$

از طرفی، داریم:

$$\alpha ^ 3 + \beta ^ 3 = 1 + \sqrt { x } + 1 - \sqrt { x } = 2$$

بنابراین، می‌توان نوشت:

$$2 + 3 \alpha \beta ( \alpha + \beta ) = 5 \\ \Rightarrow 3 \alpha \beta ( \alpha + \beta ) = 3 \\ \Rightarrow \alpha \beta ( \alpha + \beta ) = 1$$

اکنون دو طرف تساوی اخیر را به توان ۳ می‌رسانیم:

$$\alpha ^ 3 \beta ^ 3 ( \alpha + \beta ) ^ 3 = 1$$

در نتیجه، خواهیم داشت:

$$( 1 + \sqrt { x } ) ( 1 - \sqrt { x } ) ( 5 ) = 1 \Rightarrow 5(1-x) = 1 \\ \Rightarrow 1 - x = \dfrac {1}{5} \Rightarrow x = \frac {4}{5} = \frac {a}{b} \Rightarrow a + b = \boxed {9}$$

مثال هشتم اتحاد مکعب

مقدار $$107 ^ 3$$ را به دست آورید.

حل: این عبارت را می‌توان به صورت زیر نوشت:

$$107^ 3 = (100+7)^ 3$$

از اتحاد مکعب دوجمله‌ای استفاده می‌کنیم:

$$(a+b)^3 = a ^ 3 + b ^ 3 + 3 a b (a+b)$$

با قرار دادن $$a = 100$$ و $$b = 7$$، خواهیم داشت:

$$( 100 + 7 ) ^ 3 = 100 ^ 3 + 7^ 3 + 3(100)(7)(100 + 7)\\ (100 + 7)^ 3 = 1000000 + 343 + 3(100)(7)(107) \\ (100 + 7)^ 3 = 1000000 + 343 + 224700 \\ (107 ) ^ 3 = 1225043$$

بنابراین، مقدار $$107^ 3$$ برابر است با $$1,225,043$$.

جمع‌بندی

در این مطلب از مجله فرادرس با اتحاد مکعب تفاضلی، مجموع و دو جمله‌ای آشنا شدیم. پس از آشنایی با این اتحاد، مثال‌هایی را برای درک بهتر آن با یکدیگر حل کردیم.