تابع حقیقی و نگاشت در ریاضیات | به زبان ساده

ایده اصلی برای بهره‌گیری از رابطه بین متغیرها و تعریف تابع در قرن ۱۷ میلادی شکل گرفت و تحلیل خصوصیات توابع، باعث بوجود آمدن شاخه «حسابان» (Calculus) در ریاضیات شد. در آن زمان فقط «تابع حقیقی» (Real Function) یا توابع با متغیرهای «حقیقی مقدار» (Real Valued) مورد بحث واقع شده و فرض بر این بود که همه توابع «هموار» (Smooth) هستند. موضوعات مربوط به تابع و نگاشت همچنین دامنه و هم‌دامنه، بعدها در قرن ۱۹ توسط ریاضیدانان، مورد پژوهش واقع شد. بنا به اهمیت توابع و نقش آن‌ها در ریاضیات پایه و عمومی، این نوشتار از مجله فرادرس را به این گونه توابع اختصاص داده‌ایم. البته در این بین تفاوت تابع حقیقی و نگاشت (Map) نیز بیان شده و خصوصیات هر یک مورد بحث قرار می‌گیرد.

از آنجا که موضوع تابع حقیقی وابسته به مجموعه اعداد حقیقی است، پیشنهاد می‌شود مطالب اعداد حقیقی — به زبان ساده و مفاهیم تابع – به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای دامنه و برد تابع — به زبان ساده و رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده نیز خالی از لطف نیست.

تابع حقیقی و نگاشت در ریاضیات

از تابع و رابطه برای نمایش ارتباط بین دو مجموعه یا اعضای آن‌ها استفاده می‌شود. به همین جهت می‌توان توابع و موضوعات مربوط به آن را به نظریه مجموعه‌ها نسبت داد. ولی از آنجایی که این مفهوم یا ساختار ریاضیاتی، بیشتر از نظریه مجموعه‌ها مورد علاقه بوده و کاربرد دارد، در اغلب کتاب‌های ریاضی، به عنوان موضوعی کاملا جدا از نظریه مجموعه‌ها مورد بحث قرار می‌گیرد. هر چند اصطلاحات مربوط به «دامنه» (Domain) و «هم‌دامنه» (Codomain) کاملا وابسته به نظریه مجموعه‌ها هستند.

فیلم آموزش مبانی آنالیز حقیقی – جامع و با نکات کاربردی در فرادرس

کلیک کنید

منظور از «تابع» (Function) بخصوص «تابع حقیقی» (Real Function) و همچنین «نگاشت» (Mapping) در این مطلب مورد بحث قرار گرفت و تفاوت آن با «رابطه» (Relation) بازگو می‌شود. همچنین عملیات جبری قابل اجرا در بین نگاشت یا توابع نیز مورد بررسی قرار می‌گیرد.

تعریف تابع و نگاشت در ریاضیات

به طور شهودی، می‌توان تابع را یک فرآیند یا «عملگر دو دویی» (Binary Operation) در نظر گرفت که به واسطه آن هر عنصری از یک مجموعه به یک عنصر به مجموعه دیگر مرتبط می‌شود. البته نحوه ارتباط در اینجا دارای شرایطی است که در ادامه به آن خواهیم پرداخت.

به طور رسمی تابع $$f$$ از مجموعه $$X$$ به مجموعه $$Y$$ به صورت یک مجموعه است که شامل زوج‌های مرتبی مثل $$(x,y)$$ بوده که عنصر اول آن از مجموعه $$X$$ گرفته شده و مولفه دوم آن نیز متعلق به مجموعه $$Y$$ است. در این بین شرطی وجود دارد که طی آن هر عنصری از $$X$$ نباید بیش از یک بار در تابع یا مجموعه زوج‌های مرتب، به کار رفته باشد. به بیان دیگر نباید به ازاء‌ یک مقدار از مجموعه $$X$$ دو مقدار در تابع یا مجموعه $$Y$$ پیدا شود.

نکته: اگر چنین اتفاقی بیافتد، مجموعه زوج‌های مرتب را یک «رابطه» (Relation)‌ می‌نامند. پس هر تابع یک رابطه است ولی هر رابطه، یک تابع نیست.

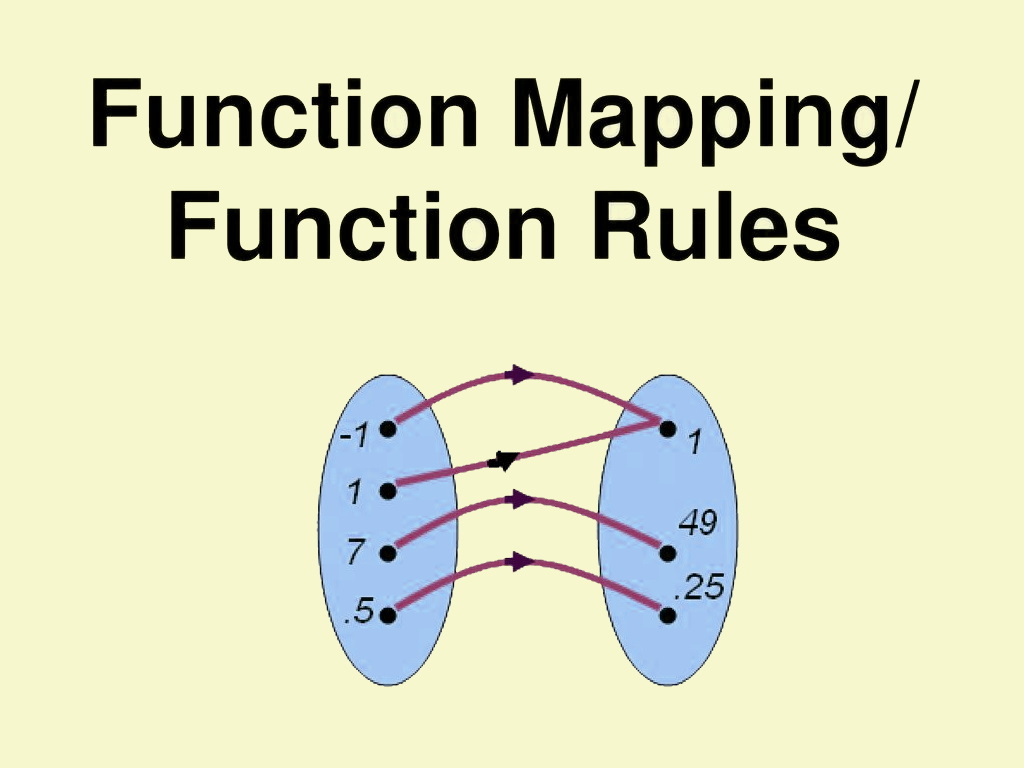
در تصویر ۱، وضعیتی را مشاهده می‌کنید که یک تابع بین مجموعه $$X$$ و $$Y$$ برقرار شده و عناصر مجموعه $$X$$ را به عناصری از مجموعه $$Y$$ مرتبط کرده است. در این حالت، مجموعه اول را «دامنه» (Domain) و مجموعه‌ دوم را «هم‌دامنه»‌ (Codomain)‌ می‌نامند.

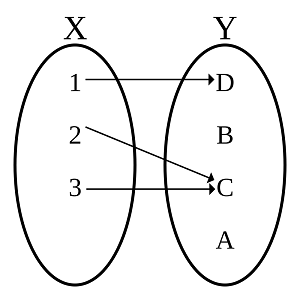
در عوض اگر چنین وضعیتی در بین زوج‌های مرتب تشکیل دهنده تابع وجود نداشته باشد، بین دو مجموعه یک رابطه (و نه تابع) برقرار است. در تصویر ۲، نمایی از یک رابطه بین دو مجموعه $$X$$ و $$Y$$ را مشاهده می‌کنید. واضح است که برای مولفه اول با مقدار ۲ در مجموعه $$X$$، دو مقدار یا مولفه در مجموعه دوم یعنی $$Y$$ وجود دارد. به همین سبب، پیوند بین $$X$$ و $$Y$$ از نوع تابع نخواهد بود و صرفا یک رابطه بین این دو مجموعه برقرار شده است. مشخص است که زوج‌هایی که باعث تخریب خاصیت تابع شده‌اند، $$(2,B)$$ و $$(2 , c)$$ هستند. در حقیقت مقدار $$2$$، به عنوان مولفه اول، در دو زوج مرتب دیده می‌شود.

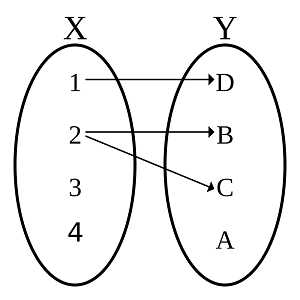
اگر زوج $$(x,y)$$ متعلق به تابع $$f$$ باشد، آنگاه $$y$$ را «تصویر» (Image) مقدار $$x$$ تحت تابع $$f$$ می‌نامند و به صورت زیر نمایش می‌دهند.

$$\large (x,y) \in f \quad \quad \rightarrow \quad \quad y = f(x)$$

مجموعه مقادیری که $$y$$ در این تابع دارد، به اصلاح «بُرد» (Range) یا «تصویر» (Image) تابع نامیده می‌شود و می‌گویم، تابع $$f$$، مقدار $$x$$ را به $$y$$ تصویر کرده است. در تصویر ۱، برد تابع مجموعه $$\{B,C\}$$ است. برای نمایش دامنه تابع $$f$$ اغلب، از نماد $$D_f$$ و برای برد آن نیز از $$R_f$$ استفاده می‌کنند.

نگاشت در ریاضیات

اغلب هر تابع را یک «نگاشت» (Map) در نظر می‌گیرند ولی بعضی ریاضیدانان، برای مفهوم نگاشت و تابع، تمایز قائل می‌شوند. برای مثال «سرژ لانگ» (Serge Lang)، ریاضیدان آمریکایی-فرانسوی، تابع را برای نگاشت‌هایی که هم‌دامنه آن زیرمجموعه‌ای از اعداد حقیقی یا مختلط است به کار می‌برد و معتقد است که نگاشت حالت کلی‌تری از تابع را شامل می‌شود.

از طرفی، اغلب منظور از نگاشت همان «هم‌ریختی» (Homomorphism) است. مثلا برای نشان دادن یک گروه هم‌ریخت از $$G$$ به $$H$$ از اصطلاح نگاشت خطی یا نگاشت از $$G$$ به $$H$$ استفاده می‌کنند. گاهی هم زمانی یک تابع را نگاشت می‌نامند که هم‌دامنه آن دقیقا منطبق با مجموعه مقادیر تابع باشد.

تابع حقیقی

یک تابع حقیقی، تابعی است که براساس متغیرهایی با مقایر حقیقی ساخته می‌شود. به این ترتیب دامنه و هم‌دامنه آن زیرمجموعه‌ای از اعداد حقیقی است که می‌تواند به صورت یک بازه نمایش داده شود. اغلب در ریاضیات ساده دبیرستان یا دانشگاهی، منظور از یک تابع، تابعی حقیقی (حقیقی‌-مقدار) است. ما هم از این به بعد در این متن هر جا از تابع سخن بگوییم، منظورمان توابع حقیقی یا حقیقی-مقدار است.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

نکته: اگر تابعی براساس مجموعه مقادیر اعداد مختلط شکل گرفته باشد، آن را یک «تابع مختلط» (Complex Function) نامیده و در حوزه آنالیز و ریاضیات مختلط مورد توجه قرار می‌گیرد.

توابعی که اغلب در ریاضیات کاربردی، مورد استفاده قرار می‌گیرند، دارای خصوصیات ویژه‌‌ای هستند. «تابع پیوسته» (Continues Function)، «تابع مشتق‌پذیر» (Differentiable Function) از این گونه هستند، زیرا رفتار بهتر و مناسب‌تری نسبت به دیگر انواع توابع دارند. چنین توابعی را به کمک نمودارها و خطوط پیوسته می‌توان ترسیم کرد.

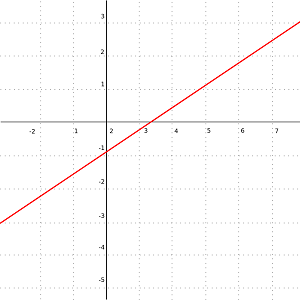
در تصویر ۳، یک نمودار مربوط به یک نمونه از تابع خطی را مشاهده می‌کنید که یک تابع هموار محسوب می‌شود. این تابع در دامنه‌اش، یک تابع پیوسته و مشتق‌پذیر است، بنابراین در گروه «توابع تحلیلی» (Analytic Function) قرار می‌گیرد.

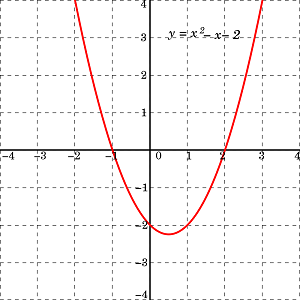
همچنین در تصویر ۴، یک تابع درجه دوم به شکل $$f(x) = x^2 - x - 2$$ را مشاهده می‌کنید که یک تابع حقیقی (از $$R$$ به $$R$$) تعریف شده است و دامنه آن همه اعداد حقیقی و برد آن نیز مجموعه اعداد بزرگتر از $$\frac{-9}{4}$$ است. همانطور که در نمودار مشخص است، این تابع، پیوسته و مشتق‌پذیر است.

نکته: برای پیدا کردن کمینه تابع، می‌توان از مشتق‌گیری و پیدا کردن نقاط اکسترمم کمک گرفت.

توابع از «عملیات نقطه‌ای» (Pointwise Operation) تبعیت می‌کنند. یعنی اگر $$f$$ و $$g$$، هر دو تابعی حقیقی باشند، مجموع، تفاضل و حاصل‌ضرب آن‌ها نیز توابعی حقیقی خواهند بود. پس توابع حقیقی نسبت به عملگرهای «جمع» (Addition)، «تفریق» (Subtraction) و «حاصل‌ضرب» (Product) بسته هستند. در این صورت داریم:

$$\large {\displaystyle {\begin{aligned}(f + g)(x) & = f(x) + g(x) \\ \large (f - g) (x) & = f(x) - g(x) \\ \large (f \cdot g)(x) & = f(x) \cdot g(x) \\ \end{aligned}} }$$

نکته مهم در این بین، پیدا کردن دامنه این عملگرها روی توابع است. دامنه‌های توابع حاصل از اجرای این عملگرها، به صورت اشتراک دامنه‌های توابع $$f$$ و $$g$$ خواهد بود. البته برای تقسیم دو تابع حقیقی باید با دقت بیشتری عملیات را انجام داد. تقسیم یا خارج قسمت دو تابع نیز یک تابع حقیقی است و به صورت زیر در نظر گرفته می‌شود.

$$\large {\displaystyle { \dfrac {f} {g}} (x) = { \dfrac {f(x)} {g(x)}} }$$

اما دامنه تابع حاصل تقسیم با حذف صفرهای تابع $$g$$ از اشتراک دامنه تابع $$f$$ و $$g$$ بدست می‌آید. در ادامه این متن به چند مثال می‌پردازیم تا با نحوه اجرای عملیات جبری رو توابع و پیدا کردن دامنه حاصل، بیشتر آشنا شویم.

مثال ۱

تابع $$f(x) = \sqrt{x-2}$$ و $$g(x) = \sqrt{x+2}$$ را در نظر بگیرید. جمع و تفاضل این دو تابع یعنی $$(f + g)(x)$$ و $$(f - g)(x)$$ را محاسبه کرده و دامنه آن‌ها را مشخص خواهیم کرد.

از آنجایی که هر دو تابع، به صورت جذر یا رادیکال یا ریشه دو هستند (و با توجه به حقیقی بودن این دو تابع)، مجموع و تفاضل ‌آن‌ها به صورت زیر نوشته می‌شود.

$$\large  (f + g)\;(x)  = f(x) + g(x) = \sqrt{x - 2} + \sqrt{x + 2}$$

$$\large  (f - g) \;(x)  = f(x) - g(x) = \sqrt{x - 2} - \sqrt{x + 2}$$

البته رابطه‌های بالا قابل ساده‌سازی نیز نیستند. از طرفی، دامنه هر دو تابع با توجه به ریشه دوم و مثبت بودن زیر رادیکال با فرجه دو، به صورت زیر محاسبه می‌شود.

$$\large D_f = \{ x \in R \quad | \quad x + 2 \geq 0 \}$$

که به صورت $$x \geq -2$$ یا بازه $$[-2 ,  \infty)$$ قابل نمایش است. حال به بررسی دامنه تابع $$g$$ می‌پردازیم.

$$\large D_g = \{ x \in R \quad| \quad x - 2 \geq 0 \}$$

که به صورت $$x \geq 2$$ یا بازه $$[2 ,  \infty)$$ قابل نمایش است. از آنجایی که اشتراک این دو مجموعه، دامنه تابع حاصل جمع و تفاضل را مشخص می‌کند، دامنه تابع $$f + g$$ با دامنه تابع $$f - g$$ برابر بوده و به شکل زیر در خواهد آمد.

$$\large D_{f + g} = D_f  \cap D_g = \{ x \quad |\quad x \geq -2 , x \geq 2 \}$$

می‌توان این مجموعه را به صورت فاصله $$[2, \infty)$$ نیز در نظر گرفت. همچنین برای پیدا کردن دامنه تفاضل این دو تابع نیز به شکل زیر عمل می‌کنیم.

$$\large D_{f - g} = D_f \cap D_g = \{ x \quad | \quad x \geq -2 , x \geq 2 \}$$

که باز هم فاصله $$[2, \infty)$$ را نشان می‌دهد.

مثال ۲

این بار به ضرب و تقسیم این دو تابع توجه خواهیم کرد و دامنه هر یک را هم به واسطه اشتراک دامنه هر دو تابع مشخص می‌کنیم. ابتدا به ضرب این دو تابع می‌پردازیم.

$$\large (f \dot g) (x) = f(x) \cdot g(x) = \left( \sqrt{x -2} \right) \left(\sqrt{ x +2 } \right ) = \sqrt{ (x - 2 )( x + 2) } = \sqrt{ x^2 - 4}$$

فیلم آموزش مبانی آنالیز ریاضی – مرور، حل مثال و تست کنکور ارشد – بخش یکم در فرادرس

کلیک کنید

اگر به قاعده اشتراک دامنه دو تابع در جبر توابع دقت نکنیم، ممکن است در اینجا با یک مشکل روبرو شویم. طبق مثال قبل، مشخص است که دامنه حاصل ضرب این دو تابع باید $$D_{f \cdot g} = [2 , \infty)$$ باشد. ولی اگر دامنه تابعی که از حاصل‌ضرب این دو تابع ساخته شده است را مشخص کنیم، به یک تناقض خواهیم رسید.

$$D_{\sqrt{x^2- 4}} = \{ x \quad| \quad x^2 \geq 4 \} = \{ x \quad | \quad x \geq 2 , x \leq -2 \} : ( \infty , -2] \cup [2 , \infty)$$

مشخص است که این مجموعه، مقادیر کوچکتر از ۲- را هم در دامنه تابع $$\sqrt{X^2 - 4}$$ دارد، در حالیکه دامنه حاصل‌ضرب دو تابع $$f$$ و $$g$$ شامل این مقادیر نیست. پس قبل از انجام عملیات جبر مجموعه‌ها، باید دامنه تابع حاصل را بدست آورده، سپس عمل جبری را انجام دهیم، هر چند در این مثال‌ها، ابتدا عمل جبری انجام شده، سپس دامنه مشخص گردیده است.

مثال ۳

این بار به سراغ تقسیم تابع $$f$$ بر $$g$$ می‌رویم. البته محاسبه تقسیم این دو تابع، ساده شدنی نیست، ولی مهم استخراج دامنه تابع تقسیم آن‌ها است.

$$\large  \left( \dfrac{f}{g} \right) (x) = \dfrac{f(x) } {g(x) }  = \dfrac{ \sqrt{x - 2}} {\sqrt{ x + 2 } }$$

دامنه تابع مربوط به تقسیم این دو تابع نیز به شکلی که در ادامه قابل مشاهده است، حاصل می‌شود.

$$\large D_{\frac{f}{g}} = D_f  \cap D_g - \{ x \quad | \quad g(x) = 0 \} = [ 2 , \infty) - \{ - 2 \} = [2, \infty)$$

اگر به دنبال تقسیم تابع $$g$$ بر $$f$$ بودیم، به رابطه‌های زیر می‌رسیدیم.

$$\large  \dfrac{g}{f} (x) = \dfrac{ g(x) } {f(x) }  = \dfrac{ \sqrt{x + 2}} {\sqrt{ x - 2 } }$$

و

$$\large D_{\frac{g}{f}} = D_f \cap D_g - \{ x \quad | \quad f(x) = 0 \} = [ 2 , \infty) - \{ 2 \} = (2, \infty)$$

به این ترتیب مشخص است که جمع و ضرب در جبر توابع، خاصیت جابجایی داشته، ولی تفریق و تقسیم، چنین خاصیتی ندارند.

موضوع دیگری که در مورد توابع حقیقی، قابل توجه و مورد علاقه است، ترکیب دو تابع و پیدا کردن معکوس آن‌ها است. این دو مطلب در نوشتارهای دیگر مجله فرادرس بررسی شده و قابل دسترس هستند.

معرفی چند تابع حقیقی

در ادامه به چند نوع تابع حقیقی اشاره کرده و خصوصیات آن‌ها را بازگو می‌کنیم. اغلب در سطوح ابتدایی و متوسطه ریاضیات، این گونه توابع زیاد به کار می‌روند.

• تابع چند ‌جمله‌ای: «توابع چند جمله ای» (Polynomial Functions) توسط چند جمله‌ای‌ها تعریف می‌شوند و دامنه آنها کل مجموعه اعداد حقیقی است. از بین توابع چند جمله‌ای می‌توان به «توابع ثابت» (Constant Functions)، «توابع خطی» (Linear Functions) و «توابع درجه دوم» (Quadratic Functions) اشاره کرد.
• توابع گویا: «توابع گویا» (Rational Functions) به صورت کسری از دو توابع چند‌جمله‌ای ساخته می‌شوند و دامنه آن‌ها نیز اعداد حقیقی است البته به جز نقاطی که مخرج را صفر می‌کنند. به این ترتیب از خطای تقسیم بر صفر جلوگیری خواهد شد.

شاید بتوان ساده‌ترین تابع کسری را به صورت $$\dfrac{1}{x}$$ در نظر گرفت که در این حالت دامنه این تابع، مجموعه اعداد حقیقی بدون نقطه یا مقدار صفر است. نمودار توابع کسری بخصوص تابع $$\dfrac{1}{x}$$ به صورت یک هذلولوی است.

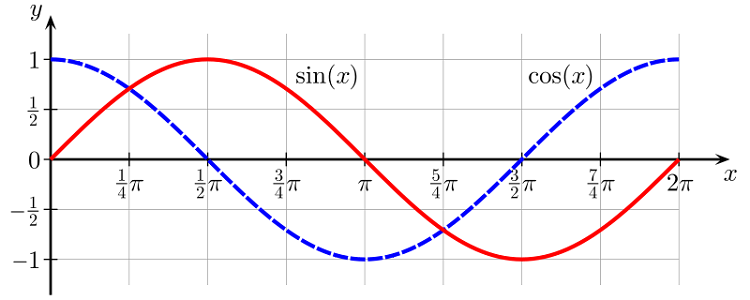
• توابع مثلثاتی: توابعی مانند $$\sin$$ و $$\cos$$، «توابع مثلثاتی» (Triangle Function) هستند که در مهندسی بسیار به کار گرفته می‌شوند. این توابع نیز اغلب در گروه توابع حقیقی جای می‌گیرند. در تصویر ۵، یک نمونه از نمودار توابع سینوس و کسینوس را در یک تناوب مشاهده می‌کنید.

توجه داشته باشید که برای یک تابع حقیقی مثل $$f$$، مشتق $$f$$ نیز یک تابع حقیقی است، به شرطی که $$f$$ مشتق‌پذیر باشد. همچنین «پادمشتق» (Antideriviative)‌ یک تابع حقیقیِ پیوسته نیز، یک تابع حقیقی است و روی یک بازه از اعداد حقیقی که در آن بازه تابع اصلی، پیوسته باشد، مشتق‌پذیر است.

برای مثال تابع حقیقی $${\displaystyle x\mapsto {\frac {1}{x}}}$$ که در موردش بحث کردیم، روی مجموعه یا بازه اعداد مثبت، پیوسته و مشتق‌پذیر است. همچنین پادمشتق آن نیز یک تابع پیوسته روی اعداد مثبت است که به آن «تابع لگاریتم طبیعی» (Natural Logarithm Function)‌ می‌گوییم.

خصوصیات بعضی از توابع حقیقی

بعضی از توابع حقیقی، دارای خواص جالبی هستند که رفتار آن‌ها را قابل پیش‌بینی می‌کند. برای مثال «تابع یکنوا» (Monotonic Function)، تابعی است که علامت نسبت تغییرات تابع به متغیر، وابسته به ترتیب قرارگیری متغیرها روی یک بازه، نیست. این موضوع به بیان ریاضی به صورت زیر نوشته می‌شود.

$$\large \text{sgn} \left( \dfrac{f(x) - f(y) }{x - y } \right)  = \text{sgn} \left( \dfrac{f(y) - f(x)}{y - x} \right)$$

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل تست کنکور ارشد – بخش دوم در فرادرس

کلیک کنید

این موضوع توسط، «توابع صعودی» (Ascending Function) و «توابع نزولی» (Descending Function) نیز قابل درک است. مشخص است که در توابع صعودی، با افزایش متغیر، تابع نیز افزایش می‌یابد، پس علامت صورت در کسر بالا، همیشه با علامت مخرج کسر یکسان است و در نتیجه این نسبت، مثبت خواهد بود.‌ در صورتی تابع حقیقی، از نوع نزولی باشد، در رابطه بالا، همیشه علامت صورت و مخرج با یکدیگر اختلاف دارند و این نسبت همیشه منفی است. بنابراین هر تابع صعودی یا نزولی، در تعریف تابع یکنوا صدق کرده، در نتیجه یکنوا خواهد بود.

نکته: با توجه به تعریفی که از مشتق و حد تغییرات تابع به متغیر داریم، مشخص می‌شود، اگر تابع $$f$$ در بازه‌ای مشتق‌پذیر باشد، مقدار مثبت مشتق، نشانگر صعودی بودن و مقدار منفی مشتق نیز نشانگر نزولی بودن تابع $$f$$ است.

اگر یک تابع حقیقی در بازه‌ای مثل $$I$$، یکنوا باشد، معکوس‌پذیر بوده و معکوس آن نیز یک تابع حقیقی است که دامنه‌اش $$f(I)$$ و تصویرش $$I$$ است. به همین ترتیب «معکوس توابع مثلثاتی» (Inverse Trigonometric Function) در بازه‌هایی که توابع مثلثاتی، یکنوا هستند، تعریف و قبل استفاده می‌شوند.

در بعضی از موارد، یک تابع حقیقی به وسیله حل یک «معادله دیفرانسیل» (Differential Equation) حاصل می‌شوند. برای مثال، توابع حقیقی $$\sin$$ و $$\cos$$ پاسخ‌های معادله دیفرانسیل زیر هستند.

$$\large {\displaystyle y^{\prime \prime } +  y = 0}$$

بطوری که معادله دیفرانسیل گفته شده، در شرط‌های زیر صدق کند.

$$\large {\displaystyle \sin 0 = 0 ,\quad \cos 0 = 1 , \quad { \dfrac { \partial \sin x}{ \partial x}}(0) = 1, \quad {\dfrac {\partial \cos x}{ \partial x}}(0) = 0}$$

نکته: توابع حقیقی ممکن است در فضاهای دو یا چند بعدی نیز مطرح شده و برای مجموعه یا فضای $$n$$بُعدی ($$R^n$$) به کار روند که هر مولفه آن یک مقدار حقیقی است. در این صورت آن‌ها را توابع حقیقی چند بُعدی یا چند متغیره می‌نامیم.

خلاصه و جمع‌بندی

در این نوشتار به بررسی تابع حقیقی و نگاشت در ریاضیات پرداختیم و تفاوت‌های هر یک را نیز بازگو کردیم. البته بحث مربوط به حسابان و عملگرهایی جبری و حد که روی توابع قابل اجرا هستند نیز در این متن مورد توجه قرار گرفت. در این بین، ویژگی‌های تابع حقیقی و تفاوت آن را با رابطه مشخص کرده و خصوصیات هر یک را بیان کردیم. همانطور که دیدید، توابع حقیقی را می‌توان به صورت یک نمودار در مختصات دکارتی یا مختصات قطبی نمایش داد. اغلب توابع حقیقی، به جز در چند نقطه، پیوسته و مشتق‌پذیر هستند. همین ویژگی‌های رفتاری، چنین توابعی را پر کاربرد و محبوب کرده است. در دروس دبیرستان و اغلب رشته‌های دانشگاهی در مقطع لیسانس یا کارشناسی و حتی مقطع ارشد، موضوع و بحث توابع به توابع حقیقی محدود می‌شود.